基于排队论的银行网点优化研究

姬 进，杨东亮，张宇坤，闫 稳，赵 君

(航空工业西安航空计算技术研究所，陕西 西安 710065)

随着我国市场经济的深入发展，各行各业都在进行着深入的变革。而作为传统优势行业的银行也在进行着一场深入的改造。银行由大量铺设营业网点到集约化收缩调整营业网点，体现了银行的市场化进程。

为了达到这一目标，可以通过对影响银行网点个数的因素进行调查。根据调查的数据进行合理的分析优化。

1 银行网点基本假设

为了对银行网点进行优化设计，需对银行网点作如下基本假设：

1)假设每个区县顾客办理业务时，不考虑银行网点的距离，即认为在一定时间内，每一个网点办理业务的人员数是平均分布的；

2)顾客请求使用服务机构(银行的窗口)，如果该机构可用，来到的顾客便占用它并使用一定的时间后离去，随后它将立即为其他来到的顾客服务或等待的顾客服务；

3)顾客来到服务机构发现没有可利用的服务后(即前面有顾客在办理业务)，可以有两种选择，等待排队或者立即离去；

4)银行各网点内服务人员的效率是相同的，即认为服务人员的服务水平是没有区别的；

5)各个窗口认为可以办理相同的业务；

6)排队实行先到先服务、后到后服务的原则，且顾客总是向较短的队列移动，没有顾客会因为队列过长而离去。

2 银行网点影响因素分析

影响银行网点数的因素可能是多方面的，银行在决定网点的设置时，考虑的因素是多方面，既要考虑银行的经济效率又要照顾到顾客的接受程度，只有综合考虑各方面的因素后才能做出正确的决断。

我们对调查的可能影响网点的数据进行了线性回归分析，通过分析可能因素与银行网点数之间的线性关系，总结出其主要因素。

回归分析是基于观测数据建立变量间适当的依赖关系，以分析数据的内在规律，并可以用于观测、控制等问题[1]。

线形回归模型如下：

该模型有两个基本假定：

1)有m个自变量x1，…，xm,它们与应变量构成线性关系；

2)偏差ε的数学期望为0，方差为σ2，并且服从正态分布。

特殊情形，若只有一个变量x,一个因变量Y，模型变为如下形式：

称为一元线性回归模型。

对于这个问题，我们采用一元线性回归模型，这里的因变量Y为银行的网点个数，自变量x1为可能影响的因素，我们对于这个问题，对每一个可能因素分别应用回归模型，如果Y与x1之间的线性关系显著，我们即可认为此因素为影响银行网点个数的主要因素。

不难发现，城镇就业、人均地区生产总值、城乡居民储蓄、在岗职工年平均工资，满足以上三个标准，可以初步认为是影响银行网点个数的主要因素。

可以求得回归模型的参数分别是：

故回归方程为：

0.0019x4.

其中x1、x2、x3、x4分别对应城镇就业、人均地区生产总值、城乡居民储蓄、在岗职工年平均工资；

我们要对线性关系进行回归模型的检验，以求Y与X之间的线性关系是否显著相关，具体的检验方法为：

1)F检验法；

2)相关系数r的评价；

3)p值检验。

从所求方程可以看出，城乡居民储蓄因素对网点个数的影响不是很大；另外我们再次进行回归模型的检验，所求的主要参数为F=33.0770,相关系数r=0.9445,p=0.0000;所以我们认为它们的线性关系显著。

下面进行残差向量的正态性的图形检验，使用MATLAB可以方便地画出如图1所示的图形。

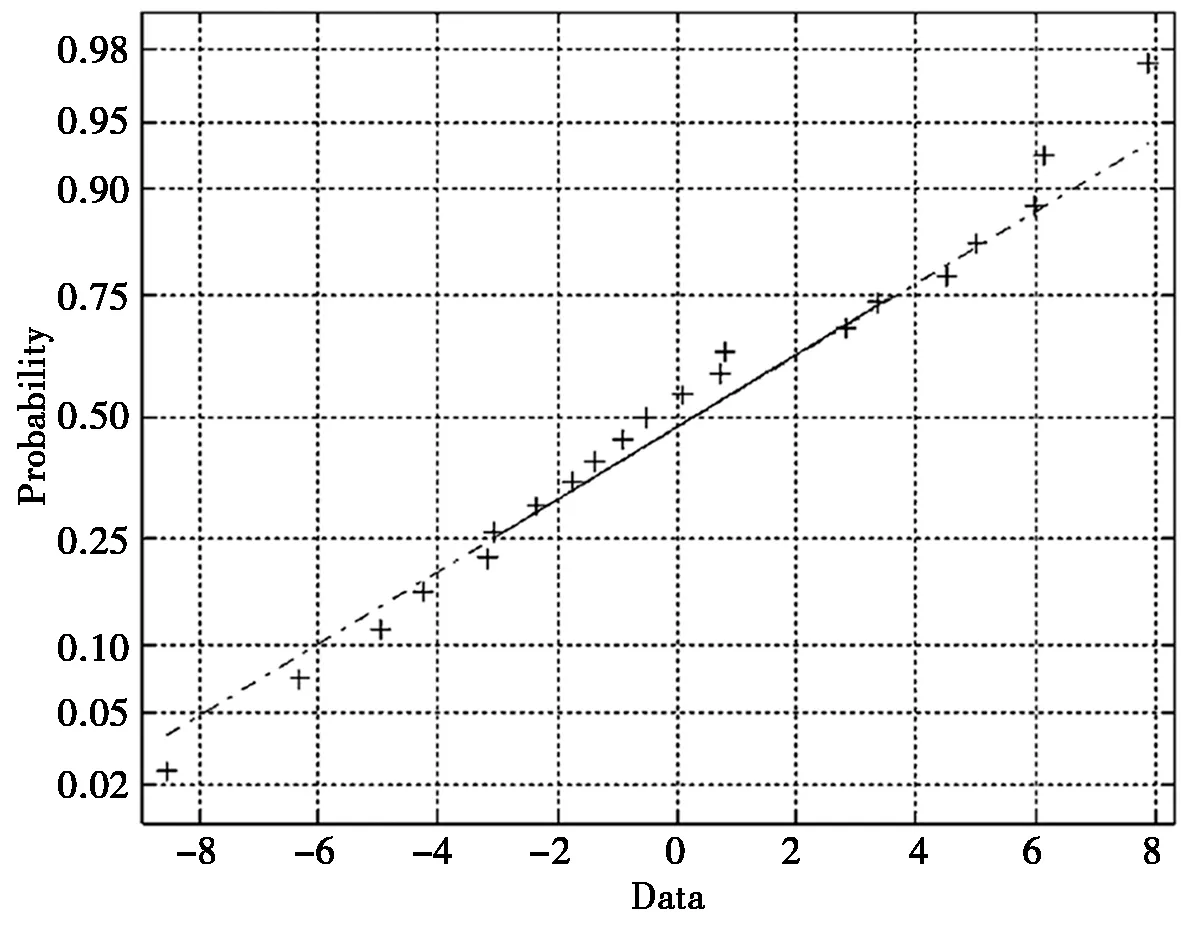
图1 残差向量的正态性的图形检验

理论上可以证明，若误差的正态性假设是合理的，那么点‘+’应该呈现散点分布在一条直线上，从上面的图形中我们可以看到，点基本上是在直线上的，故假设合理。

综上所述：我们认为城乡居民储蓄对网点个数有一定的影响，但不是主要因素，而城镇就业人数、人均地区生产总值、在岗职工年平均工资是影响银行网点个数的主要因素。

3 银行网点分布建模设计

根据网点设计给出的标准——既考虑到银行的经济效益，又照顾到顾客的接受程度。在此我们想到了排队论知识，一个银行网点可以看成是一个具有三个服务台的多通道等待模型，即M/M/c模型。

下面具体阐述M/M/c模型[2]，它是这样的一种模型：

顾客的到达服从参数为λ的泊松分布；顾客的服务时间服从参数为μ的指数分布；有c个服务台(窗口)，顾客按到达的先后次序接受服务。当顾客到达时，若有空闲的服务台就立即接受服务，若所有的服务台都忙者，则顾客排成队列等待服务，如图2所示。

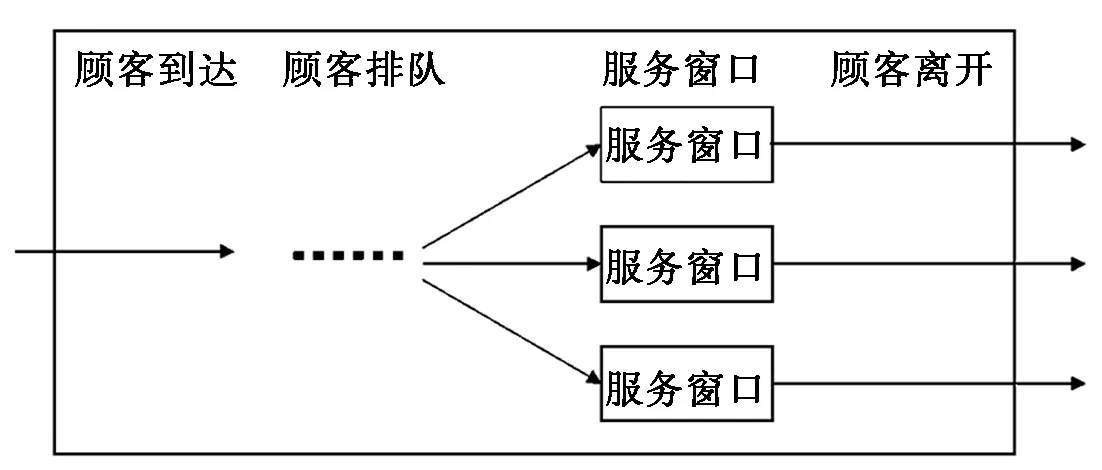
图2 M/M/c排队模型

M/M/c模型图如下：

由于系统有c个服务台，且每个服务的效率相同都是μ，于是整个系统的最大服务率为cμ,故系统的服务强度(即单位时间服务的顾客数)为：

ρ=λ/(cμ).

(1)

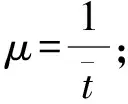
其它一些主要的效率指标有：

系统的稳态概率：

(2)

系统的平均排队长度：

(3)

顾客在系统中的平均排队时间：

(4)

顾客在系统中的平均逗留时间：

(5)

系统的平均顾客数：

Ls=L+ρ.

(6)

另外单位时间到达的顾客数我们可以这样确定，假定城镇就业人员每月去一次银行，且银行每天的工作时间为8小时，则：

(7)

式(7)中P为单月顾客总人数，N为银行网点数量。

这样我们主要计算出顾客在系统中的平均等待时间和业务窗口利用率，就可以对其网点个数的合理性进行评价。

网点分布合理应该满足下面两个指标：

1)银行窗口的利用率ρ在0.56以上且不大与1，否则就会违反M/M/c模型原理，使系统处于不稳定状态形成无限队列；

2)顾客的等待时间(顾客在系统中的平均排队时间)Wq应该在顾客愿意等待的时间范围内，即Wq∈[5,9]min。

根据上述分析的模型，可以评价银行网点分布是否合理。

4 银行网点优化设计与分析

由于在一定时间内，去银行网点办理业务的人数可以认为是固定的，服务人员的效率也基本上不变，所以只有银行的网点个数是影响窗口利用率和顾客等待时间的主要因素，因此我们分别建立二者与网点个数的关系。

我们首先分析某地区的网点设置，根据模型推导出的公式(1)、公式(4)和公式(7)建立网点个数与窗口利用率以及网点个数与顾客等待时间的散点图，如图3和图4所示。

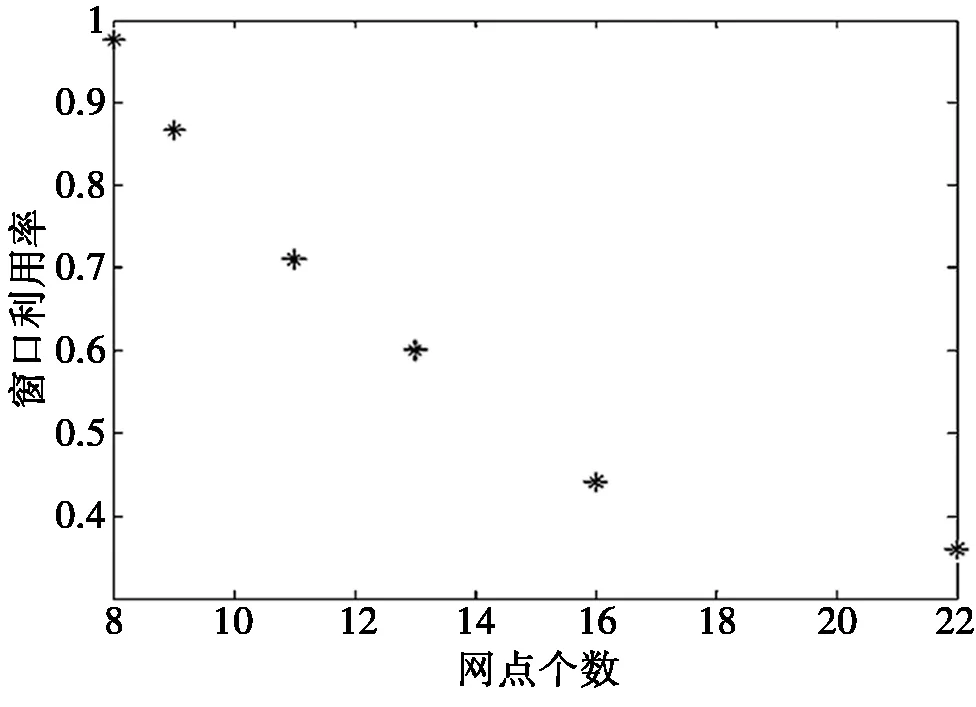
图3 网点个数与窗口利用率的散点图

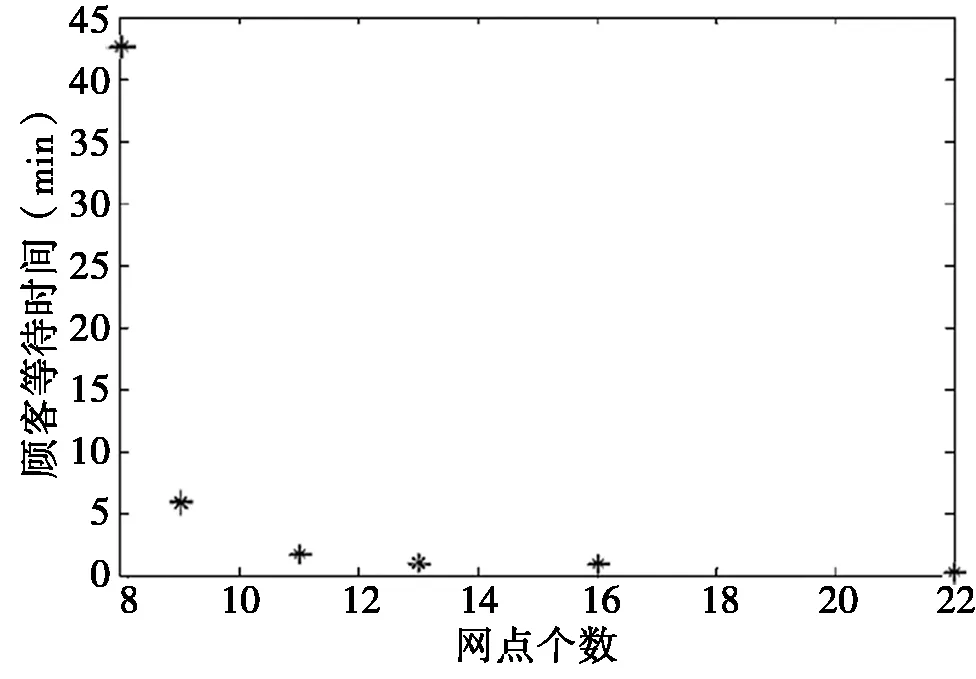
图4 网点个数与顾客等待时间的散点图

对网点个数与顾客等待时间进行多项式拟合，拟合多项式为：y=0.0009x2-0.0713x+1.4703，拟和曲线如图5所示。

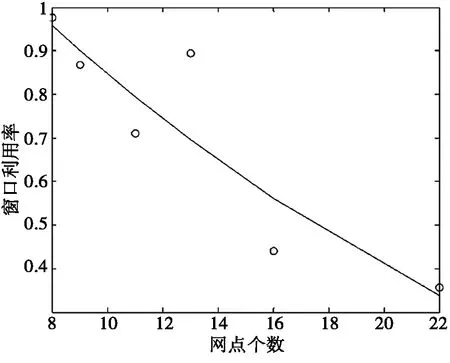
图5 网点个数与窗口利用律拟合曲线

对网点个数与顾客等待时间进行多项式拟合，拟合多项式为：y=0.4215x2-14.4372x+116.1705，拟合曲线如图6所示。

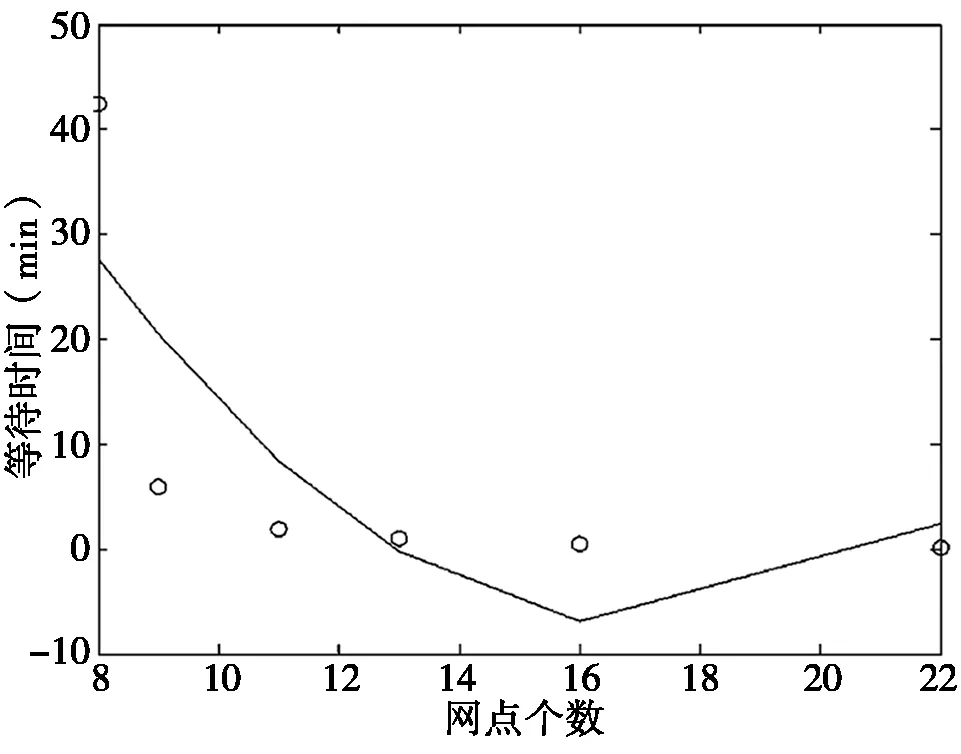
图6 网点个数与顾客等待时间拟合曲线

分析散点图和拟合图，我们发现银行网点个数设置为11～13之间时，窗口利用率和顾客的等待时间都比较合适，故该地区的网点个数设置为11到13个较为合适。

5 结束语

本文主要是分析出哪些因素可能和银行网点个数有关，然后用到了排队论中的多通道等待模型(MMc)，该模型能够很好地解决该问题中需要求解的变量，用这些评价标准可以很好地检验网点个数设置是否合理；最后我们还用到了多项式的拟合，通过拟合我们可以直观地看出合理的银行网点设置。