变频多联室外机轴流风叶的设计选型研究
2022-06-24宋培刚代文杰郑韶生
宋培刚 代文杰 郑韶生 徐 涛
(1.广东TCL智能暖通设备有限公司 中山 5128001;2.广州大学 土木工程学院 广州 510006)
引言
随着产品与技术的不断升级,用户更加关注空调器的能力、噪音、能效等指标。张曦[1]对轴流风机的安装角、转速、叶型径向扭曲程度进行建模分析,实现了安装角和转速的最优设计。谷慧芳等[2]研究了叶片安装角、风机转速以及叶片径向扭曲程度对风机性能的影响,通过数值仿真手段进行性能进行分析和预测。黄愉太等[3]利用流场仿真和实验测试研究了轴流风叶安装角与全压效率的关系,优化安装角后的风叶不仅全压效率得到了提升,噪音也进一步降低。林娟等[4]提出通过CREO软件控制风叶的弯掠角和安装角,通过风叶的参数化设计寻求风叶结构的最优设计,达到风量和效率的优化。李剑波[5]着重考察了轴流风叶叶尖涡流动现象的形成与发展,初步揭示了叶片吸力面处叶尖涡及其涡核的生成,发展和变化过程,初步把握了空调用室外机风扇转子的流动机制。王兴双[6]以空调室外机轴流风叶的叶尖涡为研究对象,结合Lighthill声学类比法的FW-H积分方程对风叶噪声进行预估,对比分析了不同安装角轴流风扇叶尖涡发展轨迹及其与导风罩的干涉作用,通过建立涡运动与声场辐射的关联,直观描述了流动的声源分布。孟丽[7]等分析由于轴流风机全压低,风量大,效率低,因此要求数值模拟精度要求高,提出通过合理处理数值建模、边界条件设置、风机出口静压确定以及混合面等几个主要问题,可以改善全压效率模拟的精度和可靠性。
从空调产品的使用需求出发,轴流风叶选型时需要综合考虑性能、噪音、效率三个关键指标,仅分析安装角度与其中的一至两项指标是不够充分的。因此,本文使用流体动力学工具,计算不同叶片安装角度与性能、噪音及效率的关系,结合模拟仿真和试验测试进行研究,找到风叶安装角的量化选型依据,以推广应用。
1 试验装置和技术路线
1.1 试验装置
本文分析的轴流风机载体为某款上出风多联机室外机,室外机容量为12 HP,主要负载为管翅式冷凝器。其中,换热器参数:双排、铜管外径d1=7 mm、片宽18.2 mm、翅片片距1.5 mm、平片结构;轴流风叶参数:外径d2=750 mm,轮毂比0.27,叶片数N=4,叶片安装角度θ=24.2 °。根据新一代产品的要求,提出以下几点设计目标:
1)提能力:0 Pa静压下的风量需要达到12 500 m3/h,提高13.6 %以上;30 Pa静压下风量仍能达到11 000m3/h。
2)低噪音:同风量噪音降低2 dB以上。
3)低能耗:提高风叶做功效率,减少电机功率损耗。
1.2 安装角
不同截面的安装角对风机效率均有不同程度的提升,且存在某个最佳安装角使全压效率最高。如图1,对叶片各截面进行分区,1#截面靠近叶根,其效率曲线平缓,安装角对效率影响不大。4#、5#、6#截面位于叶片60~100 %位置,为主要做功区,其安装角的变化对风机效率影响最大。

图1 各截面分区示意
本文选用影响最大的5#截面的安装角作为设计变量,其余截面安装角同比例调整,防止叶片扭曲。安装角逐渐增大,依次为Fan-A(θ=24.2 °)、Fan-B(θ=26 °)、Fan-C(θ=27.8 °)、Fan-D(θ=28.4 °)。
2 模型建立及计算条件
2.1 计算模型及网格划分
结合实验样机的状况,对计算模型,进行必要调整,修改后CFD模型如图2所示。其中不同范围的进口延伸对结果有影响,室外机进口直接连通大气,进口区域延伸200 mm,选择了长方体,包含了在室外机周围大气;出口区域延伸1 000 mm,保证充分发展。

图2 计算域模型
2.2 边界条件
选择稳态求解器,边界条件如下:室外机进气表面为压力入口,静压=0 Pa;出风口为压力出口,静压=0 Pa;叶轮旋转区域选用多重参考坐标方式(MRF),叶轮转速r=750 r/min。湍流模型采用标准k-ε模型,采用雷诺平均的Navier-Stockes方程组模拟三维不可压缩流动,采用双方程模型中的标准k-ε模型封闭RANS方程,如式(1)、(2),当各速度误差和k及ε误差都小于10-5且蜗壳进出口边界的流量误差也小于10-5时,认为计算收敛。

3 理论分析
3.1 风机特性
风机特性曲线可以通过实验或仿真手段获取,刘中杰[8]等指出在低静压下,轴流风扇的CFD曲线与实验曲线十分接近,但在高静压时,风机进入不稳定工作范围,流量大幅度降低,仿真很难保证准确计算出其状态下的压降。本文计算0 Pa静压下,不同安装角风扇在750 r/min转速下的静压云图,从图3可以明显看出,相同图例尺寸下,风叶安装角度从24.2 °增大到27.8 °的过程中,风叶压力面的静压逐渐升高,而从27.8 °增大到28.4 °的过程中,静压变化不明显,其压力梯度为:Fan-C≈Fan-D>Fan-B>Fan-A,因此在0 Pa静压下,Fan-C与Fan-D风量相当,且均要大于Fan-B与Fan-A。分析说明,当安装角θ=27.8 °时,继续增加安装角,并不会带来静压的提高,Fan-C的安装角是理论上的拐点。
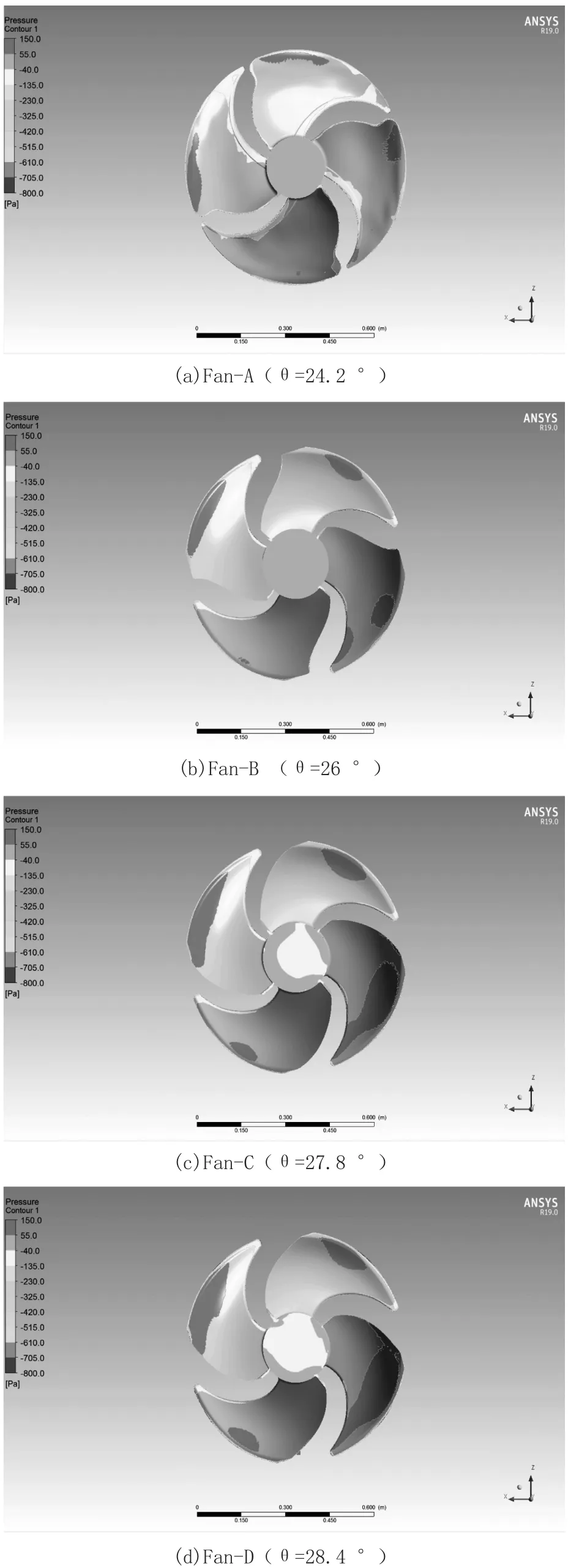
图3 各方案的静压云图
3.2 涡流分析
流场中漩涡的存在往往会引起气流产生较大的压力波动,并产生噪声。
对四种不同安装角叶轮进行数值模拟,计算不同安装角叶轮的湍动能及涡量分布。如图4、图5所示,分别清晰显示了湍动能分别为3 m2/s2、5 m2/s2时,四种不同安装角叶轮的涡量分布。

图4 湍动能3 m2/s2的涡量云图

图5 湍动能5 m2/s2的涡量云图
对于Fan-A,其安装角最小,叶顶附近的叶尖涡拉伸破裂后,随主流向下迁移,叶尖涡破裂后的轨迹在叶尖间隙中移动最远,且尾缘脱落涡明显,固其声压级应该最大。对于Fan-B,其安装角增加1.8 °,其叶顶仍然存在叶尖涡破裂后随主流向下迁移的情况,但是其迁移轨迹较短,且尾缘脱落涡改善明显,固其声压级相比Fan-A有改善。对于Fan-C、Fan-D,安装角分别增加了3.6 °和4.2 °,由于安装角较大,叶尖涡受壁面挤压后迅速沿轴向随主流流出,因此图5中未见明显的叶尖涡轨迹沿周向方向迁移的情况。
综合来看,气动噪声主要源于涡的拉伸和破裂,从涡量云图可以初步评估Fan-C和Fan-D的涡量相当,声压级当,但明显优于Fan-A和Fan-B。
3.3 效率分析
效率也是轴流风叶的重要性能参数。轴流风叶的效率通常采用静压效率。其定义为风叶的静压有效功率与轴功率的比值,具体如式(3)所示:

式中:
Nes—风扇的静压有效功率;
N—风扇的轴功率;
Ps—风扇的静压;
Qs—风扇的流量。
在轴功率的定义中,轴功率是电动机传动给风机机轴的功率,用符号N表示。除有效功率外,还包括风机转动引起的机械摩擦损失、流体克服阻力所产生的能量损失,及因风叶叶轮周围间隙产生漏气现象所引起的能量损失。显然轴功率大于有效功率。
由式(3)可知,风压一定的时候,出风风量越大,效率越高,风量与轴功率的比值可以表征风叶的做功效率。表1列出了仿真中的风量、轴功率,通过公式计算出风叶效率,可见Fan-B与Fan-C的风叶效率要高于Fan-A与Fan-D。
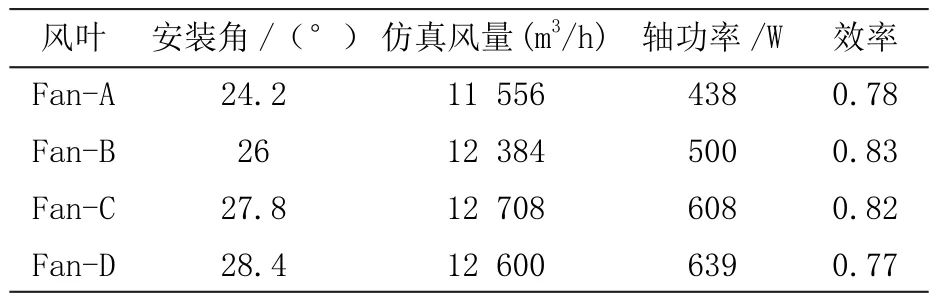
表1 各方案轴功率仿真数据
4 实验分析
为保证试验验证精度,将Fan-A、Fan-B、Fan-C、Fan-D四个方案制作成CNC手板,保证壳体、变频电机、换热器等部件一致,在同一原型机中进行风量、噪音等试验测试。
4.1 风量实验
如表2所示,在风道静压为0 Pa,风叶转速为750 r/min时,Fan-A、Fan-B、Fan-C、Fan-D随着安装角度的增加,风量先增大后减小,在Fan-C出现拐点,其风量最大。将各方案的仿真结果与试验结果进行对比,相对误差在0.2~3.7 %,满足工程使用要求,故上述仿真计算方法可行。
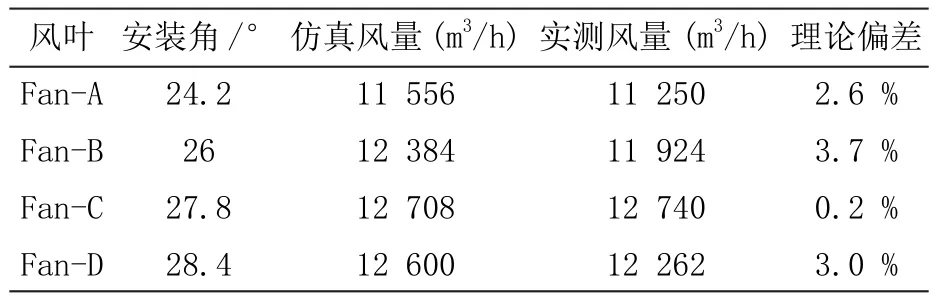
表2 各方案风量性能实验
在200 ~750 r/min的转速范围内,试验结果如图6所示,相比Fan-A,同转速下,Fan-B风量平均提升6 %,Fan-C风量平均提升13.2 %,Fan-D平均提升9.0 %。试验说明在0Pa静压下,Fan-C方案最优,其风量梯度为:Fan-C>Fan-D>Fan-B>Fan-A,与理论的静压云图分析结果一致。
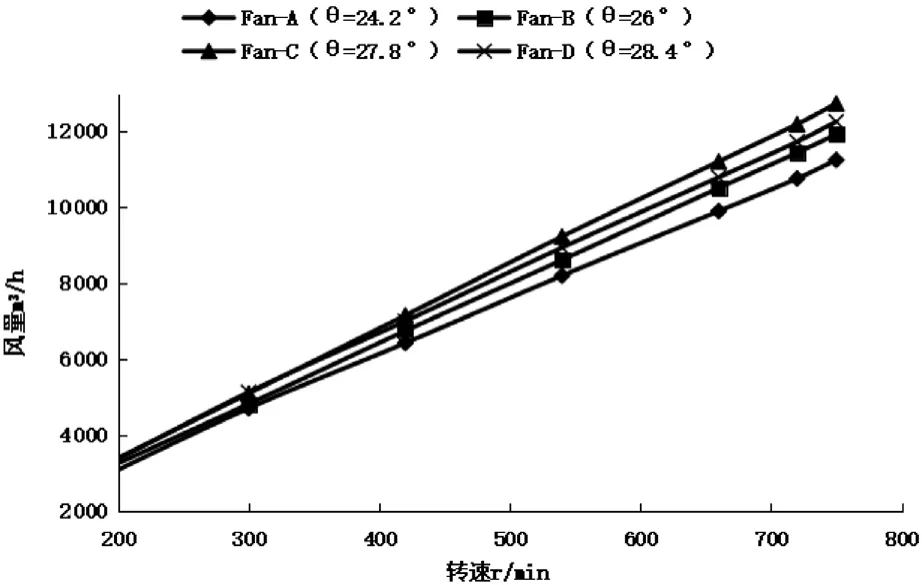
图6 各方案风量性能实验
试验结果和理论分析表明随着安装角的增大,同转速下的风量出现拐点,安装角θ=27.8 °时的风量最大。
4.2 噪音实验
试验测试整机噪音数据如图7所示,同风量下,Fan-B与Fan-D的噪音相当,相比Fan-A降低了1.4~2.6 dB,而Fan-C在同风量下,噪音值最优,相比Fan-A降低2.5~4.6 dB。

图7 各方案噪音实验
涡流分析说明Fan-A的叶尖涡移动轨迹最大,且尾缘脱落涡明显,因此其声压级最大,试验结果表明Fan-A的噪音值最大。随着安装角增大,Fan-B的叶尖涡减少了移动轨迹,改善了尾缘脱落涡,试验结果表明同风量下Fan-B的噪音值比Fan-A降低了1.4~2.6 dB,与理论分析相符。涡流分析Fan-C与Fan-D的涡量相当,声压级相当,但试验结果表面同风量下,Fan-D的噪音值比Fan-C增大了1~2 dB,分析其原因是涡量分析是在同转速下进行的,同转速下Fan-C与Fan-D的声压级相当,但同转速下Fan-D的风量要低于Fan-C,因此同风量要求提高Fan-D的转速,最终导致Fan-D的噪音值偏大,最终的噪音值试验结果为:Fan-C<Fan-B ≈ Fan-D< Fan-A。
试验结果和理论分析表明随着安装角的增大,叶尖涡运动轨迹减少,尾缘脱落涡改善明显,同转速下声压级改善。但随着安装角增大,风量出现拐点,安装角θ=27.8 °时的风量最大,相应的同风量噪音最优。
4.3 功率实验
试验测试整机功率如图8所示,Fan-B与FanC同风量消耗的功率接近,风叶做功效率接近。Fan-A和Fan-D在同风量消耗的功率接近,风叶做功效率接近。但同风量下,Fan-B和Fan-C消耗的功率明显低于Fan-A和Fan-D,因此Fan-B和Fan-C的风叶有利于提效,降低能耗。在额定风量为11 000 m3/h,此风量下,Fan-A、Fan-B、Fan-C、Fan-B的消耗功率为390 W,332 W,335 W和400 W,因此Fan-D的效率最差。

图8 各方案功率实验
试验结果和理论分析表明随着安装角的增大,风叶的轴功率增加明显,而风量增加缓慢,导致风叶做功效率先增加后减少,在安装角θ=27.8 °时出现拐点,其风叶效率最高。
5 结论
基于理论及试验分析,选定Fan-C,θ=27.8 °为新一代产品的风叶方案,该风叶在0 Pa静压下,风量达到12 740 m3/h,风量提高13 %;30 Pa静压下,风量达到11 425 m3/h;且同风量下整机噪音较原方案降低3~4 dB,同风量下全压效率提高14 %,均达到了设计目标,并得出以下结论。
1) 低静压条件下,风量仿真数据与试验数据误差小,CFD仿真具备工程指导意义。
2)风叶的静压特性与实度参数正相关,实度值的大小可以表征风叶的抗静压能力。
3)涡流图可以直观展示叶尖涡、尾缘涡的涡量情况,说明风叶噪音改善情况。
4)轴功率与风量参数可以表征风叶效率,为选择高效的风叶提供理论依据。
