基于离散忆阻的二阶超混沌系统及其动力学研究

张瑞笛，袁 方，李玉霞

(山东科技大学 电气与自动化工程学院，山东 青岛 266590)

不同于传统的电阻、电容、电感等基础电路元件，忆阻器本质上是非线性电子器件。忆阻器的提出和制备引起学术界和工业界的广泛关注[1]，引发了一系列基于忆阻性质的新一代智能电脑[2]和类脑机器[3-4]的讨论与探索。研究人员发现，当忆阻器应用于混沌系统时，能够产生丰富复杂的动力学行为，这是由于忆阻器存在内部状态变量，使得基于忆阻器的动力系统行为除受系统参数控制外，还与忆阻器内部状态变量有关，使忆阻混沌系统对初始值更为敏感。

对忆阻混沌系统丰富而复杂动力学行为的研究，有利于理解忆阻器在电路系统中的动力学行为，并构造出新的忆阻混沌系统[5]。对于忆阻器应用于混沌系统的探索取得了丰硕的成果。围绕连续忆阻器，文献[6]利用线性二次型问题的最优控制理论，实现了蔡氏忆阻混沌系统的同步方案，并利用数值仿真验证了方法的有效性；文献[7]设计了一个基于忆阻器和忆感器的混沌系统并分析了系统动力学行为；文献[8-9]研究了其构建的忆阻混沌系统中的初始位移调控行为；文献[10]基于磁控忆阻仿真器和有源荷控忆阻仿真器，设计了一个新的五阶混沌电路系统，并验证了系统数值分析的正确性。Chua等[11]将忆阻器的概念扩展到记忆系统(或广义忆阻器)的动力学系统中，将忆阻器视为记忆系统的一种特殊情况。

通常，系统可以被划分为连续系统和离散系统，据此对忆阻系统也做出类似划分。离散忆阻系统不需要复杂模拟器件进行调试，可以直接在数字平台上实现，并可用于描述离散系统的动力学特性。一些研究人员对离散忆阻系统进行了研究，如He等[12]提出分数阶离散忆阻系统模型并构建正弦映射，观察其多稳定性；通过引入离散忆阻系统的方法改善原Hénon映射的性能[13]；文献[14]提出一种基于离散忆阻的高维混沌系统，仿真表明离散忆阻不仅扩大了原系统的超混沌区域，而且提高了系统的复杂性。Bao等[15]提出一个具有两种特殊情况的代数二阶超混沌系统，实现了离散时间映射中的初始位移调控共存吸引子，并基于单片机硬件平台实现了该系统；文献[16]基于采样开关的忆阻器-电容器电路推导得到一种二阶离散映射模型，并通过相图、迭代序列和吸引盆证实了其复杂的动力学行为。文献[17-19]提出几种新的二阶离散映射构建思路，并分析了多种复杂动力学行为，如超混沌、初始位移调控等。

一般来说，与混沌系统相比，超混沌系统至少有两个正李雅普诺夫指数和更复杂的动力学特性。为了实现超混沌，一个连续系统至少需要四维空间，而一个离散系统最少只需要二维[19]，这大大降低了系统的复杂度。同时，离散超混沌系统的模型是由较微分方程更为简单的代数方程构成的，具有更高的计算效率和较低的工业成本。本研究提出的二阶离散忆阻系统在一定参数条件下可以表现出超混沌的动力学行为，说明该系统比一般混沌系统具有更加复杂的动力学特性。从安全角度考虑，超混沌系统比混沌系统具有更复杂的相空间，因此用其设计加密系统能够获得比混沌系统更高的安全性。初始位移相关的多稳定性通常是混沌系统的固有性质，如果系统产生的混沌信号在振幅和频率上可控或可改变，那么系统在安全通信中具有潜在的价值。

与传统的连续忆阻器相比，离散忆阻系统更易于在离散域系统和数字电路中得到应用[13]。研究离散忆阻系统的混沌映射及其动力学特性、利用离散忆阻系统的记忆性和非线性特性来进一步提高经典离散混沌系统的性能具有重要的意义。目前，对于离散忆阻系统及离散忆阻混沌系统的研究较少，尤其是对由离散忆阻构成的混沌系统的隐藏超混沌吸引子研究鲜有报道。本研究设计了一个基于离散正弦忆阻的二阶离散忆阻超混沌系统，利用数值仿真方法研究其丰富的动力学行为，并基于DSP平台分析系统硬件实现的可行性。

1 离散忆阻系统数学模型

根据忆阻器的定义，一个理想的离散荷控忆阻系统数学模型描述[17]为：

(1)

式中：vn、in和qn分别为第n次迭代时v(t)、i(t)和q(t)的采样值；qn+1为第n+1次迭代时q(t)的采样值；M(qn)代表忆阻值M(q)在第n次迭代时的采样值；c表示一次迭代的步长，常量。本研究使用离散正弦忆阻系统，数学表达形式为：

(2)

令c=0.004 8，设置初始条件q0=0，将离散电流源表示为in=Asin(2πfn)，其中：A表示电流源的振幅，f表示电流源的频率。通过MATLAB数值仿真模拟，可以获得离散忆阻系统模型在V-I平面的特性曲线，即离散忆阻的捏滞回线。设置激励振幅A=1，在不同激励频率下离散忆阻系统的V-I特性曲线如图1(a)所示。设置激励频率f=2，在不同激励振幅下离散忆阻系统的V-I特性曲线如图1(b)所示。很明显，离散正弦忆阻系统的捏滞回线取决于激励信号的频率f和振幅A，较小的电流信号振幅或较高的频率都会使捏滞回线更紧缩。

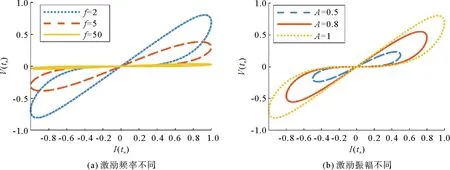
图1 不同激励时离散忆阻系统的捏滞回线

在双极性周期性离散电信号的作用下，离散化处理后的离散正弦忆阻系统在V-I平面的特性曲线为一个过原点的捏滞回线，当离散电信号频率增大时，捏滞回线的波瓣面积减小，当频率无穷大时，捏滞回线将收缩为一条单值函数[20]。由此可知，使用的离散正弦忆阻系统保持忆阻器的特性。

2 二阶离散忆阻超混沌系统

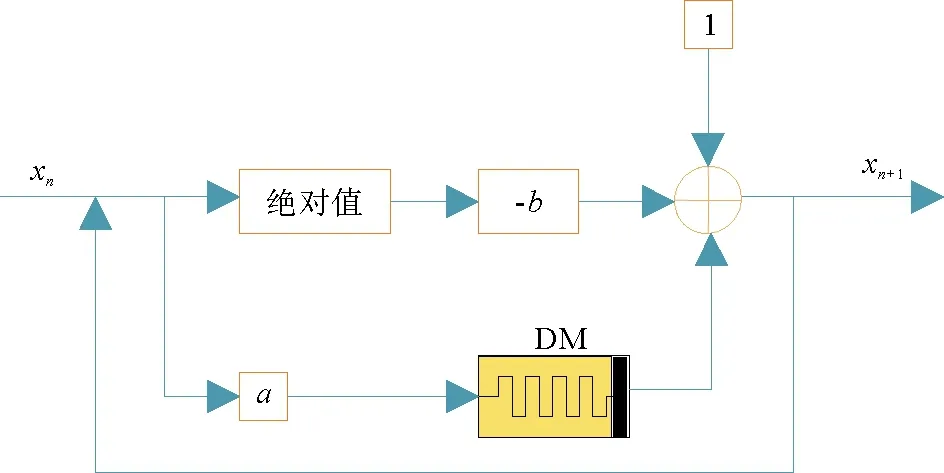
图2 二阶离散忆阻超混沌系统构造示意图

基于提出的离散正弦忆阻模型，构建一个二阶离散忆阻超混沌系统，系统构造如图2所示。图2中，a表示离散忆阻与离散系统之间的耦合强度，b为一个控制参数，DM(discrete memristor)为离散忆阻系统。利用该系统结构，可以推导出基于离散正弦忆阻的离散忆阻混沌系统的表达式

(3)

式中：n为自然数，xn和yn是在第n次取样时的两个状态值，c为离散忆阻模型中的常量。

离散系统的稳定性可用其平衡点来描述和分析。所谓离散系统的平衡点，就是当其迭代后仍回到自身的一个点。设式(3)中二阶离散系统的平衡点为S=(x*,y*)，可以通过式(4)求得：

丰富的劳动力资源和相对低廉的劳动力价格是青海发展的一项优势条件。青海是一个民族地区，包容开放多元的文化特征，有利于吸引国际人才，开展国际合作，为青海特色优势企业的发展提供强大的人才支撑。

(4)

由于式(4)所示的方程组无解，可知所提出的离散忆阻混沌系统(式(3))不存在平衡点。由于系统存在吸引子，且该吸引子的吸引域中不含平衡点，故该吸引子为隐藏吸引子，其动力学行为是隐藏动力学行为。

设置系统的初始状态(0.1, π/2)，设置参数a=1.75，c=0.004 8。当b=0.264时，系统的两个李雅普诺夫指数分别为0.143和-0.151 3，说明此时系统处于混沌状态，其隐藏混沌吸引子如图3(a)所示。特别地，当改变参数b的取值，令b=0.082，系统的两个李雅普诺夫指数分别为0.155和0.037 6，即出现了两个正李雅普诺夫指数，说明此时系统处于超混沌状态，所提出的基于离散正弦忆阻的系统是超混沌的，其隐藏超混沌吸引子如图3(b)所示。通过系统相图的离散点图可以看出，超混沌行为比混沌行为更为复杂。

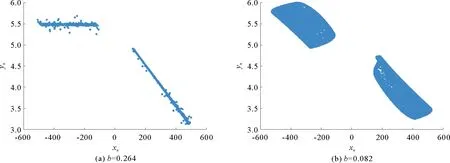
图3 系统的隐藏吸引子

3 系统动力学分析

3.1 基于参数的分岔行为

为了研究系统的分岔行为，以系统控制参数b为可变的分岔参数，b在区间[-0.5,0.5]内变化。设置系统的初始状态为固定值(0.1，π/2)，设置系统参数a=1.75，c=0.004 8。随参数b的变化，系统(3)的李雅普诺夫指数谱和分岔图如图4所示。

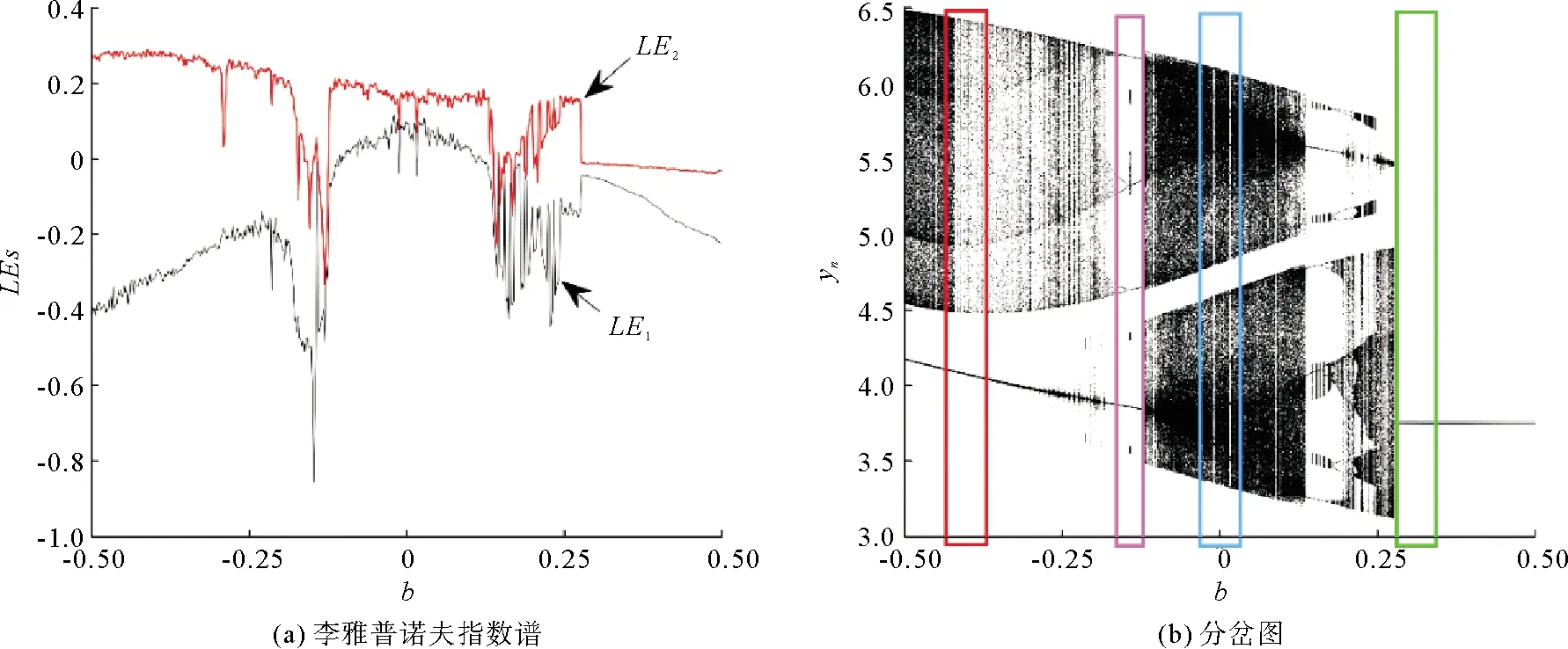
图4 系统随参数b的李雅普诺夫指数谱和分岔图

由图4看出，系统的两个李雅普诺夫指数在区间[-0.5,0.5]内存在大于0的情况，表明系统在该区间内可以产生混沌；李雅普诺夫指数谱和分岔图所反映的系统的稳定和不稳定区域是一致的，并且在分岔图中能够观察到明显的周期窗口。随着参数b的增加，系统先从反向倍周期分岔道路退出混沌，其中可以明显地看到分岔图中的混沌、多周期以及周期窗口。当b=-0.12时，系统由多周期突然变化为混沌。随着b继续增加，当b=-0.106时，系统的两个李雅普诺夫指数均大于0，表明系统处于超混沌区，分岔图中混沌区域与超混沌区域点的密集情况，说明超混沌比混沌的行为更为复杂。当b=0.137时，系统由混沌突然退化为多周期。随着b继续增加，系统由多周期经过倍周期分岔道路重新进入混沌，在其混沌区也可以观察到明显的周期窗口。当b=0.277 3时，系统由混沌突变为周期二。

参数b选取几个典型的取值，所对应的李雅普诺夫指数和时域图分别如表1和图5所示。

表1 基于参数b的系统数据

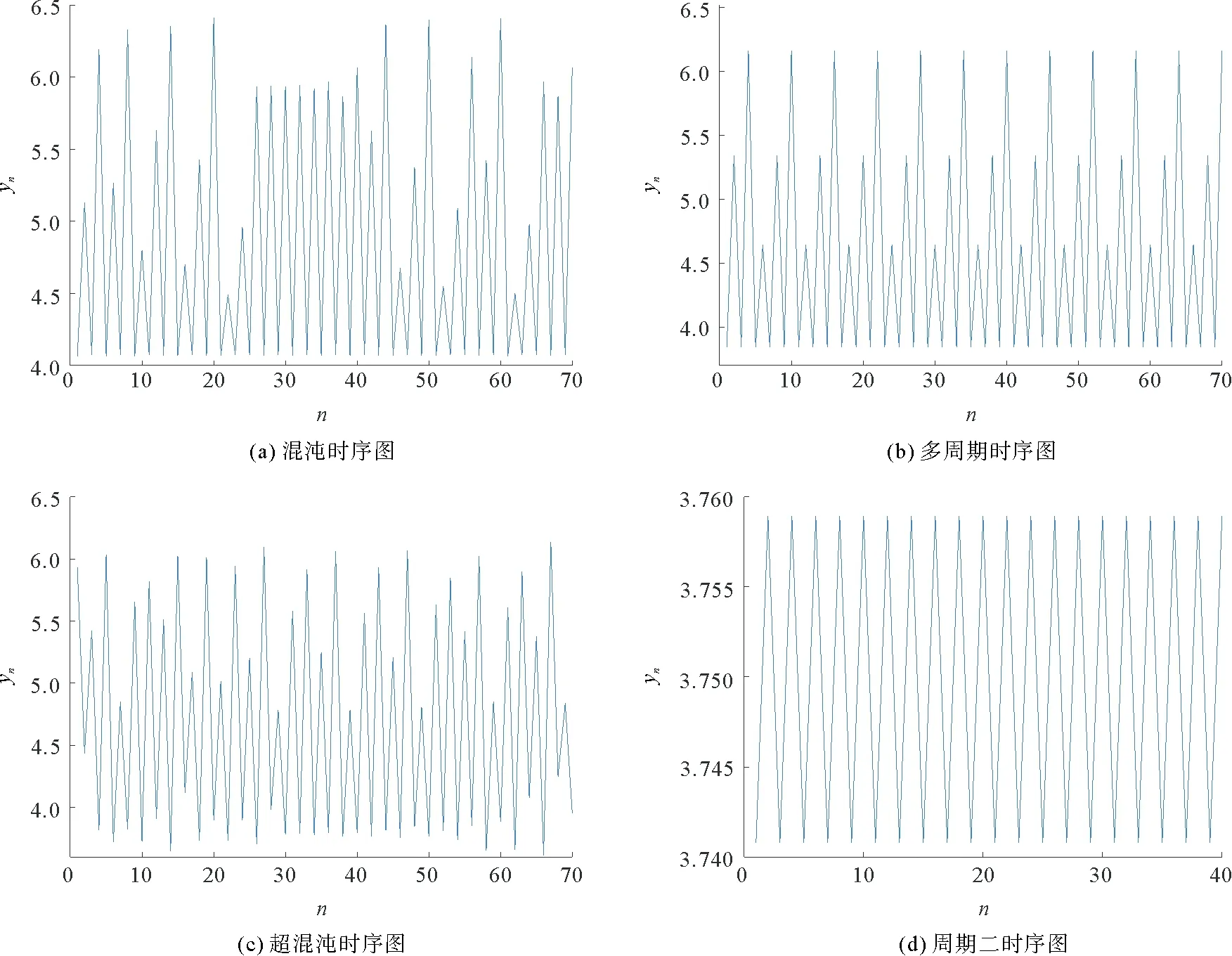
图5 系统时域图

3.2 初始位移调控行为和多稳定性

初始位移调控行为意味着一个系统可以通过偏移增强再现它的吸引子，此类系统通常具有一个周期函数，当其变量发生偏移增强时，状态方程有可能会继续保持其形式。由于式(3)所描述的系统存在周期函数sin()，因此系统可能存在初始位移调控行为，简单分析如下。

令y0=Y0+2kπ，k∈N，式(3)变为：

(5)

(6)

可以发现，式(3)与式(6)所描述的系统具有相同的形式，说明两个系统具有相似的轨迹，只是在y维度上有不同的偏移量2kπ，即该数学模型所描述的系统围绕y维度的2kπ循环，循环特性可以由系统数学模型的不变性推导出来。由系统模型(3)到系统模型(6)的转换结果可以得到，所提出的系统具有初始位移调控行为，其初始位移调控周期为2π。

固定系统参数a=1.75，c=0.004 8不变，设置初始条件(x0,y0)=(1,kπ)，k∈N。当控制参数b在[0.1,0.5]范围内变化时，绘制对应不同初值的状态变量yn的分岔图和吸引子相图。当k为奇数时，对应的分岔图如图6(a)所示，固定参数b=0.21，对应的吸引子相图如图6(b)所示；当k为偶数时，对应的分岔图如图6(c)所示，固定参数b=0.21，对应的吸引子相图如图6(d)所示。不难观察到，k为奇数时不同初始值的分岔图具有相似的结构，k为偶数时不同初始值的分岔图也具有相似的结构，但这两种分岔结构之间存在着较大差别。

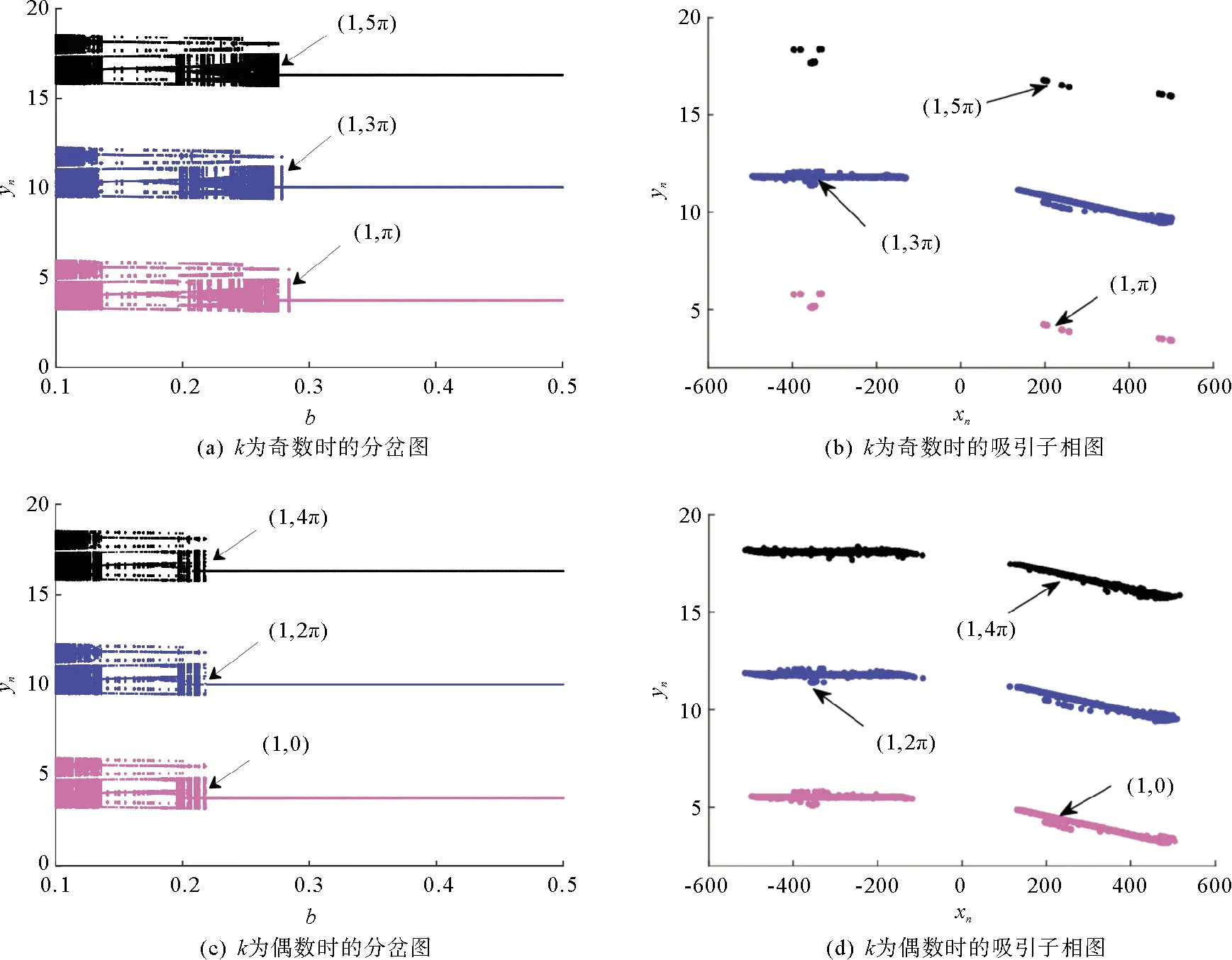
图6 初始位移调控分岔图及吸引子

图6表明，在该混沌系统中，初始位移偏置引起的初始位移调控行为是由周期为2π的初始条件y0沿y轴切换的，特别是当k趋于无穷时，会出现无穷多个初始位移偏置引起的分岔行为和无穷多个隐藏初始位移调控吸引子。

系统的初始位移调控行为也表明系统具有多稳定性。如果一个动力系统在不同的初始条件下能产生多种吸引子，那么该系统具有多稳定性，这在非线性系统中普遍存在[21]。根据共存吸引子的结构，多稳定性可分为同质多稳定性和异质多稳定性。同质多稳定性是指共存的吸引子具有相同的形状，但具有不同的振幅、频率或偏移量；异质多稳定性通常是指具有不同形状或性质的共存吸引子。

由图6可知，该系统具有同质多稳定性和异质多稳定性。如图6(b)所示，由系统李雅普诺夫指数可知，当初始值为(1, π)和(1, 5π)时，隐藏吸引子为周期隐藏吸引子；当初始值为(1, 3π)时，隐藏吸引子为混沌隐藏吸引子，即共存隐藏吸引子具有不同的性质，表明系统具有异质多稳定性。同样地，如图6(d)所示，对于不同的初始值(1, 0)、(1, 2π)、(1, 4π)，隐藏吸引子均为混沌吸引子，即共存隐藏吸引子具有相同的形状和性质，但其在y轴的偏移量不同，表明系统具有同质多稳定性。

4 硬件实验验证

数字信号处理器(DSP)是一种专门处理数字信号的微型处理器芯片，可以适应各种算法，并且能够实现对数字信号的实时、快速处理。本节利用DSP微控制器实现离散正弦忆阻系统和离散正弦忆阻超混沌系统，通过数字化实现验证数值仿真的正确性。选用的DSP评估板型号为ICETEK-VC5509-AE，主处理器为16位的TMS320VC5509A型DSP芯片，示波器型号为DSO-X3034A。将经过DSP芯片处理后的信号通过D/A转换器转换为模拟信号，并将结果输出到示波器上。

基于离散正弦忆阻系统的数学模型(式(2))，在CCS环境中编写程序并将其配置到DSP开发板中，设置参数值与图1条件相同，对于不同的激励频率f和激励振幅A，示波器得到的离散忆阻系统的捏滞回线分别如图7(a)、7(b)所示，实验结果与图1中的数值模拟结果一致，说明离散正弦忆阻系统可以通过数字化实现。

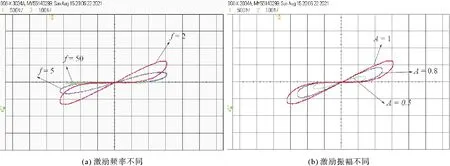
图7 基于DSP测试平台的离散忆阻系统硬件设备及其示波器波形图

同样地，由于所提出的忆阻超混沌系统是离散系统，自然可以通过数字平台来实现。根据系统(3)的数学模型，设置系统参数a=1.75，c=0.004 8，初始状态为(0.1, 1.570 795)，可变参数b取表1中的几个代表值，在CCS环境中编写程序并将其配置到DSP开发板中，然后通过示波器观察所得到的混沌序列图。为适应8位D/A转换器，将这些序列转换和放大到(0, 255)的范围，最终的实验装置硬件设备图和波形结果如图8所示。由图8可见，DSP实现的混沌与周期结果与数值仿真吻合，证明该系统硬件实现是可行的，为后续应用奠定了基础。

5 结论

本研究基于离散正弦忆阻的数学模型，提出一个新的无平衡点的二阶离散忆阻超混沌系统，借助相轨图、时域波形图、李雅普诺夫指数谱和分岔图，验证该系统具有超混沌、初始位移调控、同质多稳定性与异质多稳定性并存等复杂隐藏动力学行为。在DSP平台上实现了离散正弦忆阻系统以及二阶离散忆阻超混沌系统，通过示波器的波形图验证了系统的硬件实现可行性。该系统复杂的动力学特性丰富了对离散忆阻混沌系统的研究，为后续基于离散忆阻的混沌系统研究提供了一定的理论参考。

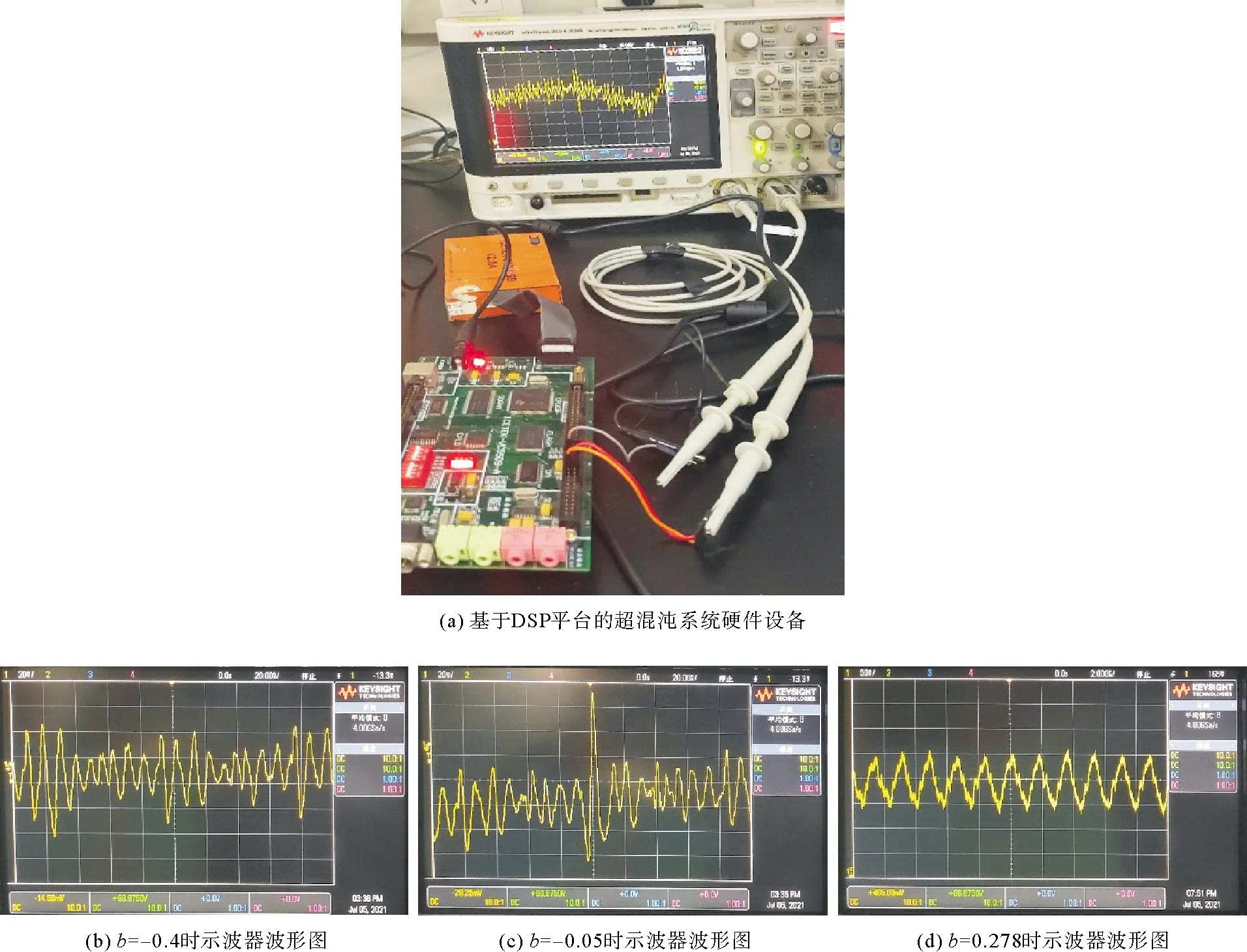
图8 基于DSP平台的硬件设备及示波器波形图