考虑能量限制的全钒液流电池储能系统建模

刘心可，李培强，张忠凯，曾靖杰

(1.福建工程学院 电子电气与物理学院，福建 福州 350118；2.智能电网仿真分析与综合控制福建省高校工程研究中心，福建 福州 350118)

电池储能技术在维持电网稳定方面优势明显，因而成为大规模储能技术的重要方案[1,2]。随着电池成本的降低和集成技术的成熟，电池储能将在电力系统中更加普及。其中全钒液流电池(all vanadium redox flow battery, VRB)充放电寿命长、使用安全、功率与容量灵活可变，在实际应用中越来越引起重视。为了得到实际工作中电池内部的数据指标，需要建立符合工程实际的电池储能模型来保证仿真结果的准确性和可信度[3]。

文献[4]对VRB的荷电状态(state of charge，SOC)等各个关键参数通过函数关系建模研究系统运行时各参数的变化过程。文献[5]建立了一个多时间尺度的能量储存模型，指出并网控制策略部分具有多时间尺度特征，对机电暂态和模型中长期动态都有影响。文献[6]以两种控制策略分别对储能进行了建模和仿真验证。有些学者使用电力系统分析综合程序(power system analysis software package，PSASP)进行储能系统建模的研究：文献[7]考虑了电力电子技术，在PSASP中搭建了并联储能型FACTS装置的暂态模型；文献[8]基于PSASP提出一种快速无振荡的复合策略建模；文献[9]基于PSASP进行了详细的储能系统机电暂态建模；文献[10]以扩展等面积法计算储能电池的最合适的工作时间长度。以上文献都考虑了无功功率限制，但没有具体建模，只是设定了无功输出的上下限，有关荷电状态(state of charge, SOC)的限制也没考虑换流器对功率的损耗。文献[11]虽然有无功功率限制环节建模，但没有研究限制环节对暂态稳定的影响。

本研究在PSASP中利用用户自定义(User-Defined，UD)建模功能建立了考虑储能能量限制的机电暂态模型，综合考虑了无功功率限制、SOC限制等环节。

1 全钒液流储能电池系统模型

全钒液流储能系统在建模中可以分成由许多单独的电池经过串并联成的电池组，以及将电池与电网连接起来的并网换流器PCS控制系统。

1.1 全钒液流电池组

全钒液流电池组(VRB)由金属电极、含有不同电价的电解液、用于离子交换的离子隔膜、分别储存正负电解液的电解池等部分组成。在储能系统的充放电的过程中，由于循环泵的压力，两种电解液从各自的电解液池进入电池本体，被电池的离子膜隔开后在电极表面发生氧化还原，实现能量转换。

正极放电反应为：

(1)

负极放电反应为：

V2+-e=V3+

(2)

本研究使用的电池模型为改进的损耗假设等效模型[12]，具体如公式(3)。以受控电压源Ustack代表电池的开路电压，Ub表示电池储能系统端口电压，通过储能系统内部电池的电流和系统端口的电流分别为I、Ib。根据电池内部损耗的属性，可以将电池的各种损耗分为RReac和RRes，分别占内部总损耗的60%和40%。泵损及附加损耗用Rfix表示，电极之间的电容用Celec表示,电压为UCelec。

(3)

储能电池单体的电动势可由Nernst方程表示为公式(4)，因为单个电池的电能有限，不能满足整个系统的需要，需要将多个电池连续串并联来提高电池的规模。用Ncell表示VRB电池的数量，VRB电池的开路电压可用公式(5)表示。

(4)

Ustack=NcellUcell

(5)

式中，E0是电池在氧化和还原过程中正极电势E0+与负极电势E0-之间的标准电极电势，单位为V；[Vi+](i=2，3，4，5)表示各个价态钒离子的浓度，[H+]表示氢离子浓度，一般为1；气体常数R，单位J/(K·mol)；T为绝对温度；n为电极反应中获得或失去的电子数，从VRB电池的工作原理中可以得到n=1；法拉第常数F，单位C/mol。

VRB电池在绝对温度T为298 K时的标准电极电势E0为：

E0=E0+-E0-=1.259 V

(6)

1.2 并网换流器PCS控制系统

换流器是储能系统运行的关键部分，它通过电力电子元件实现交直流双向变换，其四象限运行功能可以通过控制输出电压的幅度和相对于电网电压矢量的角度来改变换流器输出电流的大小及与电网电压的相位差；可根据电网的实际需求控制储能系统的有功和无功传输。

现实中的换流器最大容量一般比储能电池的最大有功输出大0%～10%[13]。在储能系统建模中，需要对换流器的能量输出做出限制，本研究通过PSASP的UD建模功能对储能系统建模，在模型中设置换流器容量上限来限制储能系统能量的输出输入。

在电力系统中，有功功率会影响系统频率，有功功率过剩时系统频率升高；而无功功率的分布对电压的大小有决定性作用。本研究的换流器采用功率外环电流内环双环解耦控制策略。其中，换流器的功率外环控制采用频率/有功控制，电压/无功控制，内环采用电流环控制。在暂态仿真过程中监测电网母线的角频率和电压的偏差值推导该母线的有功和无功缺额，通过换流器控制储能系统有功无功的出力调节电网的稳定性。

在储能电池工作的过程中，还需要监控电池的荷电状态SOC。SOC在数值上为电池剩余容量Estack与额定容量EC的比值，表达式为公式(7)，取值范围为0～1，SOC降低到0意味着电池电量耗尽，当SOC上升到1时，意味电量充满。

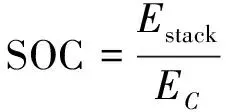
(7)

在全钒液流电池系统中，在正负离子浓度的平衡状态下，SOC是离子浓度的比值，其中，正极中：

(8)

负极中：

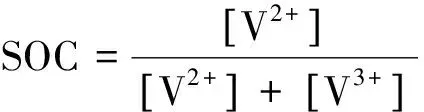
(9)

假设正负极所用电解液浓度相同、两边的反应动力学相平衡，则SOC=SOC正=SOC负。因此，在T=298 K时，VRB的单体开路电压公式(4)可以推导成公式(10)所示：

(10)

其中，SOC随着储能系统的工作过程变化，设某一时刻电池的荷电状态表示为SOCt，SOCt+1表示在单位时间后电池的荷电状态，即：

(11)

式中，Δt表示单位时间；ΔSOC表示荷电状态在单位时间内的变化量；令储能电池的容量为Ec，Ps和I表示电池的充放电功率和充放电电流。

实际上，电池运行有许多限制，物理特性和电池充电/放电状态应作为其能量限制条件。建立满足电气要求的机电暂态模型，需要在运行过程中忽略电池自身的动态变化特性对机电暂态模型的影响。设定充放电时SOC的上、下限值分别为SOCmax，SOCmin，储能电池的最大、最小输出功率Pmax，Pmin不因SDC的变化而变化。

2 考虑能量限制的储能系统控制策略

2.1 储能功率限制环节设计

2.1.1 换流器的SOC限制环节

根据电力系统的规定，为保护电池，在储能系统工作的过程中需要测定荷电状态SOC的值，当SOC超过[SOCmin,SOCmax]范围时，储能系统应该停止工作，限制环节控制有功功率输出为0，使系统停止输出或输入有功功率。

以储能系统控制环节的输出值作为储能电池的输出功率，输出值为正，意味着系统放电；输出值为负，意味着系统吸收功率给电池充电。

根据电池的有功变化可以求得电池的荷电状态的变化值ΔSOC，进而计算出电池的实际SOC来限制电池的充放电深度，避免电池长期过充或过放损坏电池，从而延长储能系统的使用寿命，提高储能系统的工作效率。根据公式(11)和充放电效率公式(12)，设计得到SOC限制环节流程图如图1所示。

图1 SOC限制环节流程图Fig.1 SOC limit link flow chart

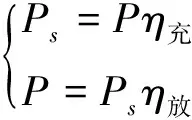
(12)

式中，Ps是电池的充放电功率，P是整个储能系统的充放电功率，换流器的充放电效率分别是η充和η放，无论充电放电，经过换流器都会有能量损耗。

图1中，1/s是积分功能框图；X1/X2是除功能框图，输入端口X1为分子，输入端口X2为分母；判断正负可以利用UD模型中的比较模块COMP，比较模块的具体含义是当输入端1口>输入端2口时输出为0，否则输出为1。

当输入P小于0时，第一个比较模块输出为1，第二个比较模块输出为0，再分别乘上P，则输出口1输出P，输出口2输出0，P大于0正好相反，如此将正负区分开。当有功功率小于0时，对电池进行充电，使得SOC值增加，当有功功率大于0时，使电池放电，所以SOC值减小。当SOC在区间内输出1，当SOC超出范围，输出0。

2.1.2 换流器限制环节

受材料和技术限制，一个换流器所能承受的最大输出功率是有限的，所以换流器的实际容量必须根据情况设置其上限。

(13)

式中Pmax为储能系统充放电最大有功功率；Qmax为最大无功功率；P为有功功率输出；Q为无功功率输出；S为换流器的容量，比储能电池最大有功功率大0%～10%。

有功功率输出与储能系统自身有关，不需要计算，无功功率限制环节数学模型为：

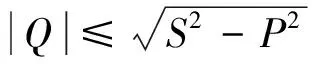
(14)

当Q大于0时，

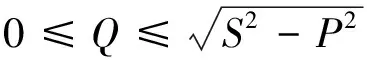
(15)

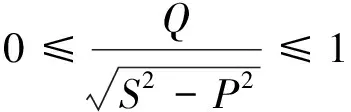
(16)

(17)

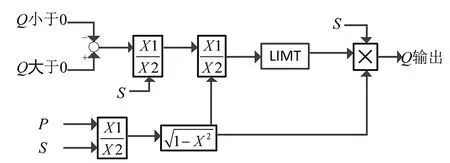
图2 无功限制模块流程框图Fig.2 Flow chart of reactive power limiting module

其中，框图LIMT是限制功能，超出上限后输出上限值，当储能系统准备输出的无功功率Q<0时需要将Q乘以-1变为正数，经过限制后需要再变回负数，在此设定一个正负指示，当Q<0时正负指示输出为-1，将无功的值恢复成负值。最后将经过限制模块后的无功功率乘以正负指示，得到最终的无功输出。

2.2 储能控制环节设计

2.2.1 外环控制器设计

换流器外环的频率/有功控制，电压/无功控制，都可以采用典型PI控制器来实现。以角频率和母线电压的实际值与基准值做差，得到ΔW、ΔU作为输入信号经PI控制器分别得到有功指令Pset和无功指令Qset，并且外环输出量传输到内环作为输入量，公式为：

(18)

式中Kωp、Kvp分别为PI控制器比例控制的比例系数；1/s是拉式积分算子，作用是积分计算；Kωi、Kvi分别为PI控制器积分控制的积分系数。

2.2.2 内环控制器设计

在得到外环传递的输出量后，将它作为控制策略的内环电流环的基准值，经过PI控制器生成电力电子开关的脉冲宽度调制(pulse width modulation，PWM)信号传递给滤波器，再将有功、无功各自前馈解耦，产生PWM信号，详细过程见文献[14]。最后对换流器的并网电流进行控制，运用等效变换和零极点相互抵消的原则，可以将内环控制近似等价于两个独立的一阶惯性环节，即：

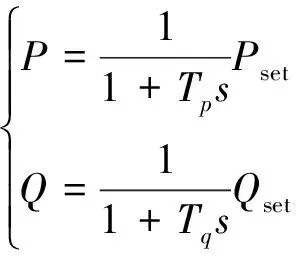
(19)

式中，Tp、Tq为控制系统响应时间常数。P、Q为储能输出的有功无功。

3 基于PSASP的控制策略模型

PSASP的用户自定义UD建模功能搭建的模型只能以节点电流作为输出量[15]，必须设计一个转换环节将储能系统输出的有功无功功率换算为电流源电流实部和虚部，以电流的形式来调节电网的频率和电压的波动。

设S=P+jQ为储能系统在安装节点注入的视在功率，令UR、UI为并网点母线电压U的实、虚部，IR、II为注入电流I的实、虚部，则

S=UI*=(UR+jUI)(IR-jII)

(20)

其中展开公式(20)得到P、Q：

(21)

求解上述方程组，得

(22)

(23)

根据式(22)～(23)可以搭建储能电池机电暂态仿真模型的接口部分。

储能系统的机电暂态模型显著降低了模型的仿真难度，基于第2节，本研究使用PSASP7.0，利用其中的用户自定义UD建模功能，构建储能系统的机电暂态仿真模型，如图3所示。框图的具体含义参见文献[15]，信号含义见表1。

图3 PSASP UD模块储能系统模型Fig.3 Energy storage system of PSASP UD module

表1 UD模型信号具体含义

4 算例仿真分析

根据搭建的储能系统机电暂态仿真模型，在PSASP仿真平台上进行了仿真试验，使用了该软件自带的CEPRI-7网络标准算例进行计算，仿真设置积分步长0.01 s，仿真总时长15.00 s，并验证了其有效性，网络的结构如图4所示。

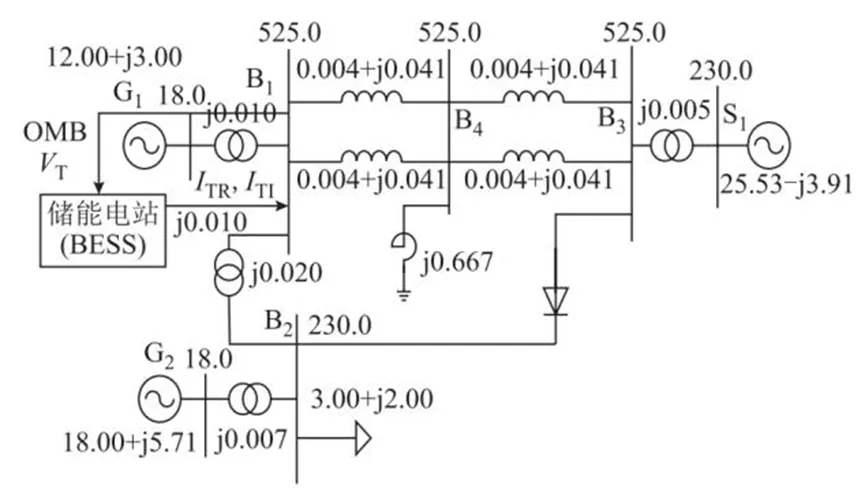
图4 CEPRI-7网架Fig.4 CEPRI-7 grid

将S1作为平衡节点，选择系统中的常规潮流计算作为初始暂态值参与时域仿真，得到潮流计算参数后进行短路测试。当仿真运行到0.02 s时，在母线B3和母线B4之间设置单回路A相接地短路故障；后在t=0.15 s时由继电保护装置工作将短路部分断开；在t=0.70 s时自动重合闸成功，监控电网母线电压与功角的变化。

4.1 不同无功限制策略的比较

将本控制策略与直接设置无功上限的控制策略对比。设置系统的基准容量SB=100 MV·A，P=1.5 pu(pu表示标幺值)，死区设置0.01，将储能系统接在B1母线处，设置无功限制环节换流器容量比储能电池有功输出大10%，所以S=1.65 pu。如果是直接设置无功上限，由于P=1.50 pu，S=1.65 pu，当有功输出达到上限时，Q极限值为0.69 pu。此时储能的有功无功输出曲线和母线电压曲线输出的前3 s如图5所示。

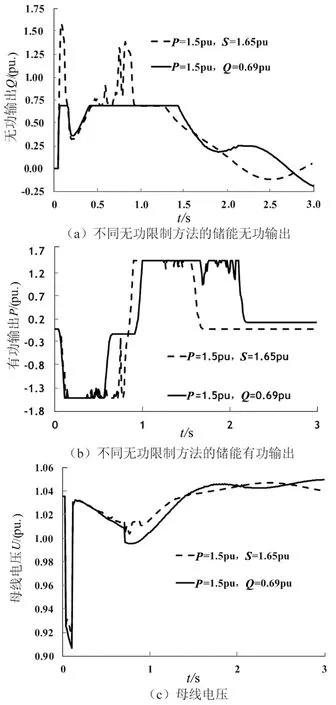
图5 不同无功限制方法的储能有功无功输出与母线电压变化Fig.5 Energy storage’s active and reactive power output and bus voltage change with different reactive power limiting methods

由图5(a)、5(b)可见，由于有功输出不是一直保持在极限值，所以本控制策略在有功未达到极限时无功功率的极限值将大于0.69 pu。如图5(c)所示，本控制策略在电压跌落初期时更加抑制母线电压的跌落幅度，之后电压的震荡幅度也要小。所以使用本控制策略的无功功率的极限值将会是一个随着有功输出变化的变化量，在调节电网稳定方面会更加灵活。

4.2 限制环节在不同大小的储能模型中的适用性

不同大小的储能电池有着不同的最大有功功率输出，需要配备不同容量的换流器。为了验证控制策略的适用性，将在B1母线处，接入最大有功功率输出不同的储能系统并配备相应容量的换流器，令储能系统充放电的最大有功功率分别为0.1、0.5、1.5 pu；设置换流器容量S分别对应为:0.11、0.55、1.65 pu；初始荷电量SOCt0=0.5，死区设置0.01。仿真计算出储能电池在不同最大工作功率下，发电机功角、母线电压还有储能系统充放电有功功率变化曲线如图6所示。

由图6各个曲线可以看出系统故障后的震荡幅度都随着储能系统的充放电功率的增大而减小，并随着时间做减幅震荡，可知系统发生故障后储能系统能够很快响应，平复系统的波动，说明所建立的能量限制模块具有良好的实用性，适用于不同规模的储能系统。

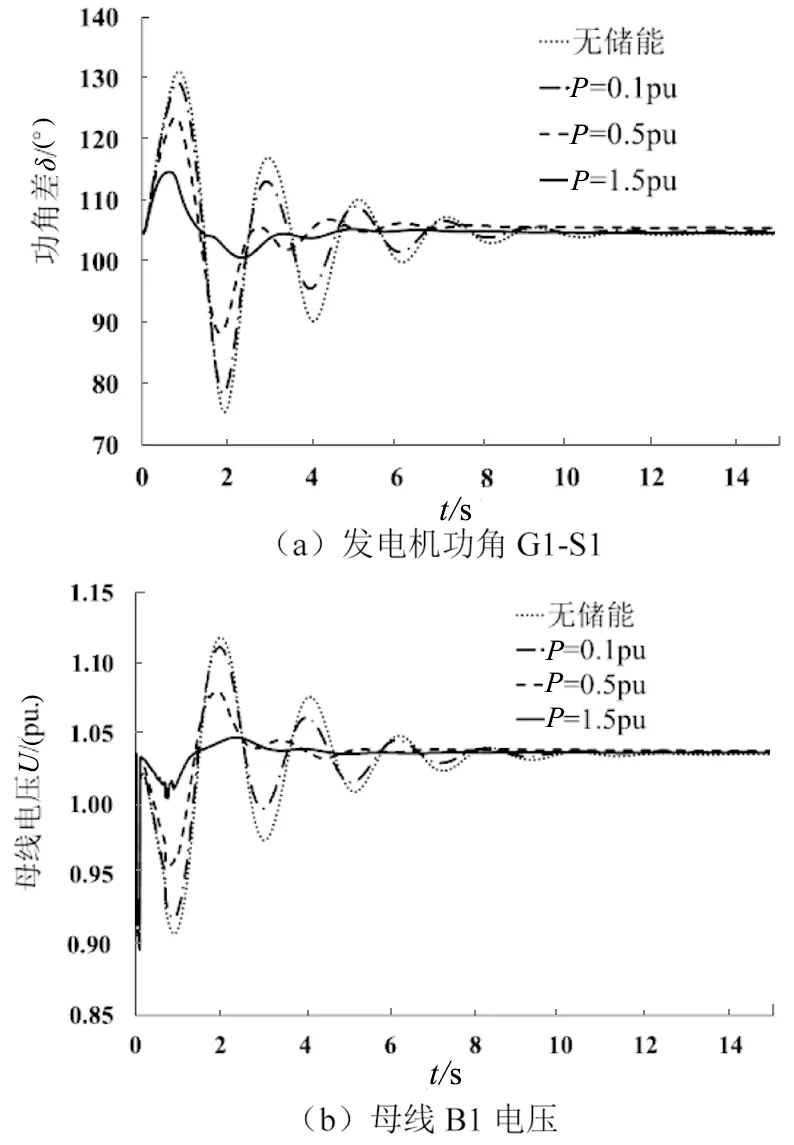
图6 不同储能不同工作功率下的发电机功角、母线电压和有功输出Fig.6 Generator power angle, bus voltage and active output under different energy storage and working power

5 结语

本研究基于PSASP建立拥有限制环节的全钒液流电池储能系统建模并进行仿真分析，并通过CEPRI-7算例来验证该模型的工程实用性。现实中的储能设备由于材料、温度等物理限制，不可能无限大的输出或输入能量，在模型的建立中必须考虑它的换流器容量限制，设置能量限制环节来限制功率传输。仿真结果中的电压幅值以及母线频率说明该模型既能通过限制储能系统的无功输出与输入，防止储能系统的功率传输超过换流器能够承受的极限，又能根据储能系统的实际有功功率及时调整无功输出功率的上下限，充分发挥储能系统对电力系统的调节稳定作用。不同大小的储能电池配备不同容量的换流器，可以更有效调节储能电池的无功输出。