让学生把数学“画”出来

蒋明玉

数形结合是一种重要的数学思想。对大脑的科研成果表明，大脑的两个半球具有不同的功能，左半脑功能偏重于抽象的逻辑思维，讲究规范严谨，如数的运算、代数式的运算、逻辑推理、归纳演绎等。右半脑功能则偏重于形象思维，讲究直觉想象，自由发散，如猜想、假设、创造等。左、右半脑的功能各有特征，如果互相补充就会使大脑功能更加健全和发达。数形结合就同时运用了左、右半脑的功能，在培养形象思维能力时，也促进了逻辑思维能力的发展。

一、利用数形结合思想，帮助理解算理

在数学教学中，教师要充分调动学生原有的知识经验，利用数形结合思想，帮助学生深刻理解算理，引导学生多角度地探索算理的形成过程，逐步培养学生利用“旧知”创造“新知”的能力。

案例1 利用“旧知”创造“新知”

在教学“整数除以分数的计算法则”时，在复习的基础上，教师出示例题：一辆汽车[25]小时行驶18千米，1小时行驶多少千米？教师引导学生根据“速度=路程÷时间”，列出算式：18÷[25]。

师：这是整数除以分數，请同学们想一想，该怎样计算？

生：可以把分数化成小数来计算，

18÷[25]=18÷0.4=45（千米）。

生：我觉得这种方法有局限性，当除数不能化成有限小数时，用这种方法就不能计算出正确的结果。

生：因为分数除以整数（0除外），等于分数乘以这个整数的倒数。我猜想整数除以分数也只要用整数乘以分数的倒数。18÷[25]=18×[52]=45（千米）。

师：这种计算方法究竟是否正确呢？下面大家一起来探究“整数除以分数”的计算法则。

（教师引导学生根据题意画出如图1的线段图）

师：根据图1的线段图，你们能推算出1小时能行驶多少千米吗？

生：从图1中可以看出，如果把[25]小时行的千米数看作1份，那么1小时行驶的千米数应该为18千米的[52]倍。求1小时行驶多少千米，就是求18千米的[52]倍是多少。18÷[25]=18×[52]=45（千米）。

生：[25]小时行驶18千米，就是2个[15]小时行驶18千米，可以先求出[15]小时行驶多少千米，列式为18÷2=18×[12]（千米）。又因为1小时是5个[15]小时，所以求1小时行驶多少千米是要算18×[12]×5，根据乘法结合律，可以得到：18÷[25]=18×[12]×5=18×[52]=45（千米）。

师：从上面同学们的回答可以看出，整数除以分数只要怎样计算就可以了？

生（异口同声）：整数除以分数，等于整数乘以这个分数的倒数。

（正当教师准备组织学生练习时，一个学生发现新的方法）

生：老师，我利用商不变性质，同样可以推出整数除以分数计算方法：18÷[25]=（18×[52]）÷（[25]×[52]）=18×[52]。

上述教学过程，学生的思维形式可以分成三个层次。第一层次是直觉思维形式，即由“因为分数除以整数（0除外），等于分数乘以这个整数的倒数。从而猜想整数除以分数也只要用整数乘以分数的倒数，18÷[25]=18×[52]=45（千米）。第二层次是形象思维形式，教师引导学生根据题意画出线段图，从而使学生借助直观图形展开思考，从整体上理解18÷[25]=18×[52]=45（千米），使学生经历了多种思考策略的比较与沟通，培养了学生的形象思维能力。第三层次是逻辑思维形式，由一个学生联想已学过的“商不变的性质”推导出18÷[25]=（18×[52]）÷（[25]×[52]）=18×[52]。这是一种逻辑思维形式，是学生利用“旧知”学习“新知”的表现。

二、利用数形结合思想，探索数学规律

借助“形”的生动和直观性认识“数”是数形结合的重要方法之一。学生在生动有趣的活动中观察、寻找图形的特点，结合图形从不同的角度观察得出不同的数学规律。教师可以通过数形结合思想，训练和培养学生数学直觉思维能力、发散思维能力和创造性思维能力。

案例2 找规律

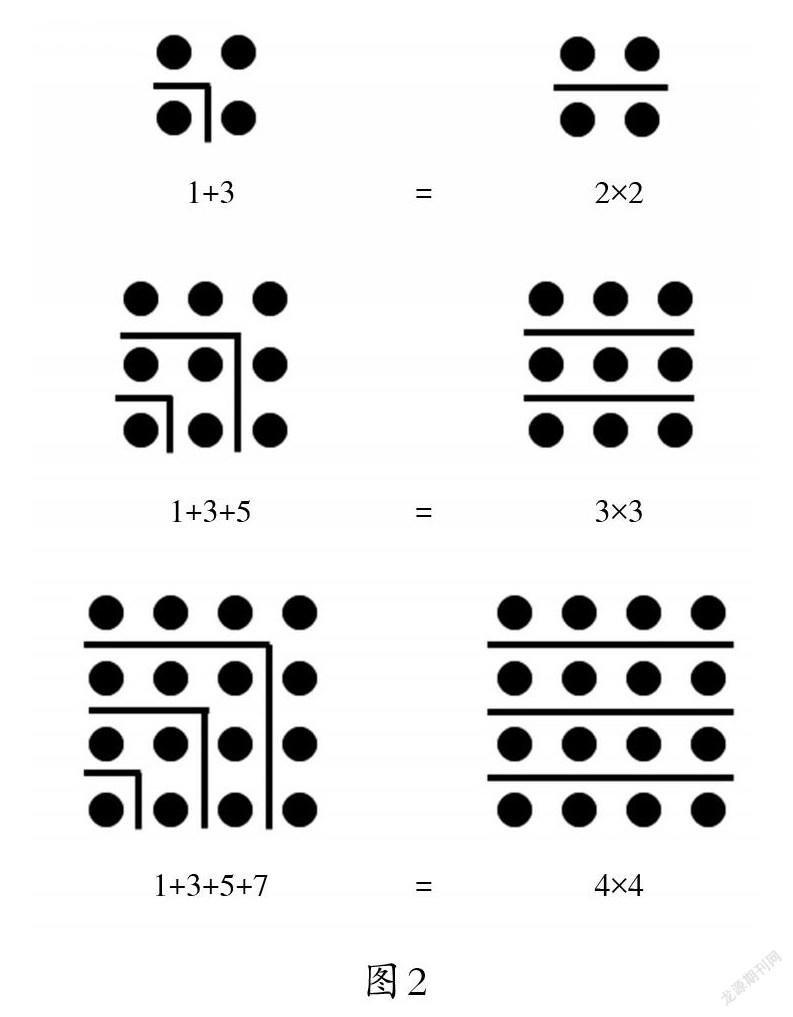
如图2，教师依次出示图中的右边部分，分别说说是由几个小圆点组成的。想象一下，第4幅图会是什么样子的？一共有多少个圆点？

师：通过刚才的观察，我们发现每幅图的圆点总数都可以看作是两个相同的数相乘的积，这些算式还可以用平方数的形式来表示。那刚才我们是怎样观察的？

生：横着观察的。

师：如果我们换个角度观察，直接出示“ ”划分的部分（图2中左边）。求每幅图的圆点总数又可以列成怎样的算式？

师：这些式子也是表示每幅图圆点的总数，和刚才的算式是否相等？

（板书：1+3=22 ，1+3+5=32，1+3+5+7=42）

生：从1起连续奇数的和等于奇数个数的平方。

生：从1起连续n个奇数的和等于n的平方（n2）。

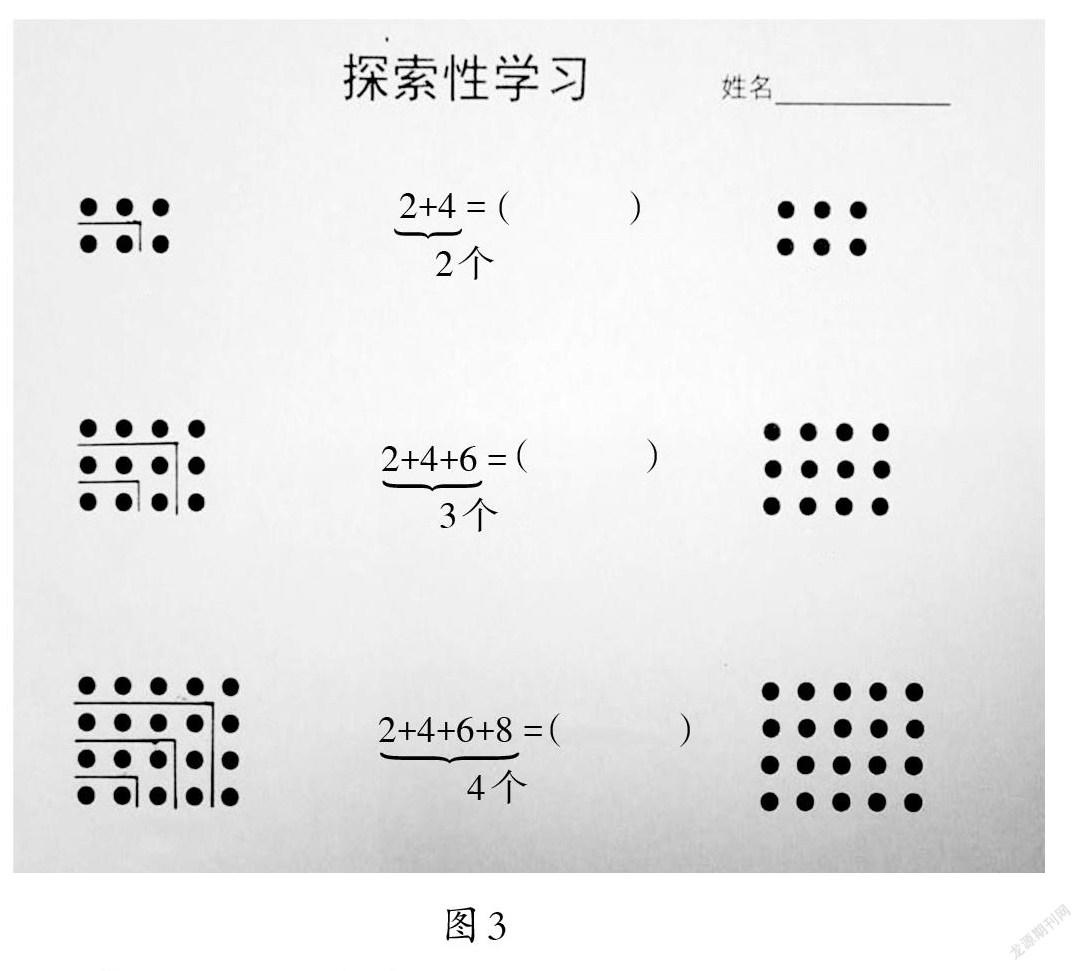
师：如图3，老师出示3个算式：2+4、2+4+6、2+4+6+8。你们能在图中画一画、分一分，使每幅图的圆点总数能用右边的式子来表示吗？

（学生在图3左边一列中独立划分后反馈）

师：如果换个角度再观察这组图（图3），你还能用什么式子来表示每幅图的圆点总数？在右边一列图中分一分，并用算式表示。

生：从2起连续n个偶数的和等于n乘以比n大1的数，即n×（n+1）。

生：从2起连续n个偶数的和等于n的平方加n，即（n2+n）。

史宁中教授说：“数学教学要培养数学直观，数学的直观是‘看’出来的，不是‘证’出来的。”利用数形结合思想来培养学生的数学直观是很重要的。数形结合方法是借助“形”的生动和直观认识“数”，通过观察前3幅图，学生从整体上观察图形的圆点排列特点;然后，想象一下第4幅图会是什么样子的。一共有多少个圆点？进而作出大胆的猜想、合理的假设，并得出试探性的结论，训练了学生数学直觉思维能力。教师引导学生主动而有效地观察图形，培养学生从图中读懂重要信息并整理信息的能力，让学生体会图形对数学规律形成的意义。教师应让学生经历观察、操作、归纳、类比、猜测等过程，发展合情推理能力，初步感受图形的美和推理的价值。

三、利用数形结合思想，巧妙解决问题

在分析、解答问题时，常常需要根据题目把题意“画”出来，启发我们全面分析问题，便于从不同角度去看图与思考，巧妙地解决问题。

案例3 创新解法

甲、乙两个容器共有溶液2600克，从甲容器中取出[14]，从乙容器中取出[15]，两个容器共剩溶液2000克，求两个容器原来各有溶液多少克？

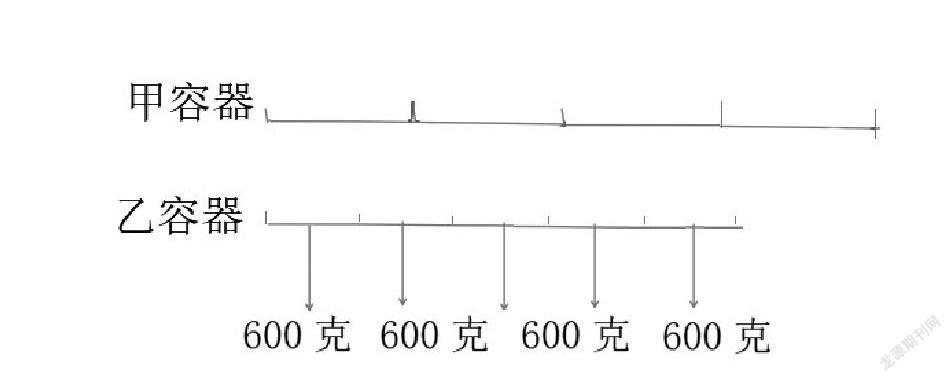
此题可以引导学生利用数形结合思想，画线段示意图进行分析，根据题意：从甲容器中取出[14]，从乙容器中取出[15]，两个容器共剩溶液2000克，可以知道甲容器的[14]+乙容器的[15]=2600-2000=600（克），图中有4个600克，学生很容易看出乙容器的[15]=200克。

列式为：4×600=2400（克），求出4组（甲容器的[14]和乙容器的[15]）的和，由2600-2400=200（克），求出乙容器的[15]等于200克。由200×5=1000（克），求出乙容器有溶液1000克。由2600-1000=1600（克），求出甲容器有溶液1600克。

小学生的思维是从具象思维逐步向抽象逻辑思维过渡，但这时的逻辑思维处于初级阶段的。教师利用数形结合思想，将学生的思维逐步引向深入，“变”中找“不变”，巧妙解决问题。把形象思维与抽象思维有机地结合起来，能够有的放矢地帮助学生多角度、多层次地思考问题，有助于学生养成多向性思维的好习惯。

（作者单位：江苏省丹阳市华南实验学校东校区）