基于PSO-KPLS的教师科研绩效预测
2022-06-23白晓波
黄 玲,白晓波
(西安工程大学管理学院,陕西 西安 710048)
0 引 言
高校教师的科研无论是其个人还是单位,都是一个无法回避的问题,绝大多数高校,都建立了对本单位教师科研考核办法,通常都有具体的量化指标,以促进教师和单位科研绩效的提升。而如何提高教师和单位科研绩效,受多种因素综合影响。为此,很多学者对此进行了研究。马秀萍[1]针对当前高校科研考核中的问题,提出了相应的激励方法,如薪资、精神情感等。于滨等[2]从超标准薪酬的角度分析了这种激励方式对高校科研的走向影响。其他,如文献[3-5]主要研究了高校教师的科研绩效评价机制,文献[6-8]分析了高校科研绩效的影响因素。文献[9]基于聚类算法对高校教师科研绩效进行评价,罗宇等[10]、龙粲妍[11]、钱玲[12]有别于文献[3-5],主要在不同背景下,研究了科研绩效评价的指标体系,如基于协同平台、应用型本科高校和“双一流”等为研究背景,或立足于高校特色,研究成果具有高校背景特色。使用关键词“高校教师科研绩效”在知网搜索,共231条记录,对其分类归纳,其研究主要分为3大类,一是对科研绩效激励机制研究,二是评价方法,三是科研绩效的影响因素,且多以定性方法为主。
通过文献回顾发现:高校教师科研绩效受多种主、客观因素的综合作用,单纯地以一种方法或者视角研究一个综合问题,很难把握未来的发展趋势,这就难以建立科学、有效的评价和激励方法。而高校教师科研绩效,受多因素高维空间向量的影响,其影响具有强烈的非线性和不确定性。因此,利用学院过去6年的教师科研数据,结合核偏最小二乘法[13](Kernel-based Partial Least-Squares, KPLS)建立预测模型,对下一个聘期教师科研绩效做出预测,进而制定更加合理的激励与考核办法。
1 PSO参数寻优KPLS
KPLS中,常用的核函数有多项式核和高斯核。在高斯核中,核参数取值方法[14]c=rmσ2,该参数的取值对拟合结果具有强烈影响,取值不准确严重影响预测精度。因此,基于粒子群[15](Particle Swarm Optimization, PSO)算法对该参数进行寻优,提出了PSO-KPLS算法。
1.1 核偏最小二乘法(KPLS)
Trejo和Rosipal教授[13]提出核偏最小二乘法,其基本原理是,通过非线性核函数将输入空间映射到高维特征空间,在特征空间中构建线性偏最小二乘回归,从而实现原始输入空间的非线性建模。核偏最小二乘算法的详细步骤如下[16]。

Step1计算核矩阵。
(1)
利用高斯核函数计算矩阵元素,核函数表示如下。
(2)
其中,cl(l=1,2,…,p)表示高斯核函数尺度。
Step2对核矩阵K中心化处理。
(3)
Step3随机初始化Y的得分向量u。
Step4计算特征空间中X的得分向量th并进行归一化。
(4)
Step5计算Yh的权值向量ch。
(5)
Step6计算Yh的得分向量uh并归一化。
(6)
Step7重复Step4~Step6,直到th收敛。
Step8将矩阵K、Y缩小,重复Step3~Step7,取得p个t、u。
(7)
(8)
以下为训练样本的拟合公式。
(9)
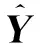
预测样本拟合公式为:
Yt=KtU(TTKU)-1TTY
(10)
Kt=Φ(xnew)Φ(x)T
(11)
xnew表示新采样的数据,x为输入训练数据,Y为输出训练数据,Kt为新数据对应的核矩阵,Yt为预测结果。
1.2 PSO-KPLS算法
关于KPLS的相关应用及研究,如文献[17-18]将其分别应用于高抗多离群点的近红外光谱数据分析中。Liu等[19]提出了动态并行KPLS方法,并将其应用于污水处理过程的监测。Said 等[20]提出了改进的动态核偏最小二乘法,并应用于非线性故障检测。这些都扩展了KPLS的应用场景,提升了KPLS的适用性。但是,在相关应用和研究中,忽略了核参数对算法性能的影响,因此,接着提出了PSO-KPLS算法。该算法,本质上是利用PSO群体寻优思想,求得合适参数使得KPLS拟合的均方根误差最小。具体表示如下:
min RMSE(s,f)
(12)
式(12)中,s表示因变量样本向量,f表示拟合值向量。但是,拟合值主要受到高斯核函数中参数c的影响。这是因为c=rmσ2,r是一个常数(1≤r≤10),m是输入空间的维数,σ2是维度l输入数据的方差。进而也就转化为对参数r的寻优。整个算法的流程如图1所示。

图1 PSO-KPLS算法流程图
PSO-KPLS算法详细步骤如下:
Step1使用均匀分布,生成n个在[1,10]之间的随机粒子ri。
Step2for each particlei
初始化速度vi和位置xi
评估粒子i,并设置pBesti=xi
end for
gBest=min{pBesti}
Step3For each particlei
Step3.1 form=1:n
forj=1:n
用公式(2)计算核矩阵K(m,j)
end
end
Step3.2 用公式(3)对核矩阵K中心化
Step3.3 ford=1:m
初始化u;
初始化t;
end
Step3.4 ford=1:m
forj=1:100
用公式(4)~公式(8)非线性迭代求解t,u
end
end
Step3.5 用公式(9)~公式(11)计算预测值
Step3.6 计算RMSEi
end
观点1:思政课教师职责定位的“三种角色”说。黄冈职业技术学院的侯利平认为,高校思政课教师应扮演“三种角色”,即马克思主义理论的宣讲者、学生思想问题的释疑者、坚定的马克思主义实践者[3]6。
Step4判断RMSEi是否满足约束条件
fori=1 ton
if RMSEi>threshold){
vi=vi+c1×rand()×(pbesti-xi)+c2×rand()×(gbesti-xi)
(13)
xi=xi+vi
(14)
评估粒子i。
If(fit(xi) if(fit(pBesti) gBest=pbesti }else{ break for循环,进入Step5。 } end for 返回Step3 Step5结束。 式(13)更新粒子速度,式(14)更新粒子位置。vi表示粒子i的速度,rand()表示(0,1)之间的随机数,xi是粒子的当前位置,c1和c2是当前学习因子,通常,c1=c2=2,vi的最大值为Vmax>0,若vi>Vmax,则vi=Vmax。 教师的科研绩效受到多个指标影响,一是个人基本特征,如年龄、学位、指导的硕士、博士生人数等,二是组织环境因素,如学院的激励政策、科研补贴等,因此,每个教师每年的科研绩效采用如下方式表示: D=φ(C,O) 其中,φ为C、O到D的函数映射。其中D=(a,p,r,b,k,h)表示教师的科研产出。a表示文章数,p表示专利数,r表示省部级以上项目数,b表示专著数,k表示科研经费(万元),h表示教师参与的学术会议数。为了综合表达教师每年科研绩效,建立D与(C,O)之间的函数关系,将D的计算方法进一步表示如下: f(t)=at+pt+rt+bt+st+dt (15) C=(w,g,l,s,d)表示与教师相关的属性,w表示教师学位,s表示指导的硕士生人数,d表示指导的博士生人数,结合文献[21-23]对影响因素进行分析,年龄系数g和教学工作量系数l对f(t)的影响到底是正向还是负向影响,与具体取值相关。g的取值和年龄ω相关,随着年龄的增长,其创新能力和体力相对降低,对科研绩效起到负向影响作用,具体表示如下: (16) l的取值与δ(实际教学工作量)和b相关,其取值如下: (17) b是教师需要完成的基本课时数。 O=(e×β,Q)表示组织属性,e表示人均科研补助数,β是e的权重,取值方法如公式(18)。β为e的权重,取值如下: (18) 即科研经费越多,对科研成果的影响越大。Q是[-5,5]之间的随机数,表示组织O的环境因素对教师t不确定因素的影响,但是,这个影响因人而异,所以,这里用随机数表示。 为了验证PSO-KPLS的有效性,以学院近6年来的教师信息和科研数据为基础,利用式(15)计算每个教师的科研绩效,然后以最近3年部分教师的信息作为输入,对老师科研绩效进行预测。具体实验环境为:处理器:Intel(R) Core(TM) i5-4200U CPU @1.60 GHz 2.30 GHz,内存:4 GB,操作系统:Win7(64位),Matlab 7。由于篇幅所限,这里选取部分教师的信息及科研绩效,如表1所示。 表1 教师信息及科研绩效样本 再利用上述方法计算出其他老师过去6年,约438条记录的科研绩效,检验PSO-KPLS算法性能。 在PSO-KPLS迭代寻优的过程中,结束迭代是以实际RMSE的值是否符合RMSE取值为依据。因此,对于PSO-KPLS的性能分析,主要通过以下2个方面来分析。 1)从处理数据时间和精度2个方面来阐述,为此,主要通过在不同RMSE要求下,探究程序寻优次数、运行时间和实际的RMSE的关系。 2)在相同的基础数据条件下,同时使用KPLS建模,对PSO-KPLS与KPLS,及其他文献中的方法在拟合误差、预测误差和运行效率上进行对比分析。 从理论上分析,RMSE对算法的运行效率有影响,即要求拟合精度越高,也就是RMSE越小,就需要算法花费更多的时间进行参数寻优,反之,若RMSE越大,则算法找到符合精度要求的最优参数,所需时间越少。具体实验过程如下,首先取RMSE=2,然后取RMSE=5,针对每个取值分别运行10次程序,并记录其运行时间、实际RMSE的值以及寻优获取的核参数c。实验结果如表2所示。 表2 PSO-KPLS 的2组实验结果 在表2中,可以看出RMSE的取值对运行时间和精度都有着重要影响。当RMSE=2时,寻优次数均值为25.6次,运行时间均值为34.3562 s。在核参数c=20.877时取得最小均方根误差。当RMSE=5时,寻优次数均值为5.5次,运行时间均值为7.4403 s,在核参数c=45.1726时取得最小均方根误差。 为了进一步分析RMSE取值对算法性能的影响,继续分别取RMSE=8、RMSE=10,各运行10次,分别计算寻优次数运行时间均值,如表3所示。 表3 RMSE取值与寻优次数、运行时间均值 对40次实验结果统计以后,效果如图2所示。 从表3、图2所示的结果中可以得出结论:RMSE越小,即拟合精度越高,寻优次数和程序运行时间都明显增加,若对拟合精度要求越低,算法的寻优次数和运行时间也明显降低。在寻优次数、运行时间和RMSE之间呈非线性递减关系。 图2 RMSE与计算次数、运行时间关系图 为了进一步说明PSO-KPLS的优势,本文利用相同的样本数据,再利用标准KPLS、文献[19]的DCKPLS、文献[20]、文献[24]和文献[25]中改进的KPLS进行实验,并利用第一次达到相同精度要求时(RMSE均值小于特定阈值)的参数,对各自的拟合误差、预测误差以及运行效率作对比分析。其结果如表4所示。 表4 PSO-KPLS与KPLS及其他改进的KPLS的性能对比 从表4的对比结果可以看出,寻找最优参数时,在满足相同精度要求的情况下,PSO-KPLS的性能明显优于KPLS,不论是拟合误差和预测误差。另外,由于PSO-KPLS融入了粒子群参数寻优,其效率明显高于KPLS的人工参数调优。PSO-KPLS在要求RMSE小于2时,其效率约为KPLS的26倍。在要求RMSE在小于5、8和10的情况下,PSO-KPLS效率分别约是KPLS效率的73倍、118倍和144倍。其他如文献[19]和文献[20],其参数都需要多次手动调优,才能达到指定的精度要求,而且由于文献[20]对KPLS进行了简化,在建模时丢失了部分信息,从而在RMSE要求为2时,通过25次参数调优后未能达到精度要求,所以其结果用“--”表示。文献[24]利用模因算法进行参数寻优,以提高KPLS的回归预测能力。文献[25]利用了遗传算法进行参数寻优。从整体的实验结果分析,在达到相同的RMSE要求时,PSO-KPLS具有较高的精度优势,而文献[25]具有较高的效率优势,所用时间更少,两者性能相近。文献[24]的效率和精度介于PSO-KPLS和文献[25]的GA-KPLS之间。 为了对PSO-KPLS的预测性能进行验证,在设定精度要求为RMSE<8时,对部分教师科研绩效进行预测,并重点与文献[24]和文献[25]的预测效果进行对比,结果如图3所示。 图3 PSO-KPLS拟合效果图 从图3的结果看出,PSO-KPLS的预测结果更接近真实值,其次是文献[25]和文献[24],但是这两者的结果比较接近。这也符合3.2节的实验结果。 高校教师科研绩效考核与激励,是激发教师科学研究和学科建设的重要途径。但其科研绩效模型受多种因素影响,有正向的激励因素,也有负向制约因素,如何使用数学语言对其准确表达,并有效把握其发展趋势,对于管理者制定科学合理的激励机制,促进教师职业发展、提升单位学科影响力具有重要意义。因此,基于既有数据,定义了教师科研绩效的表达方法,提出了PSO-KPLS预测算法,并详细阐述了利用PSO对KPLS算法进行参数寻优的详细过程,再根据样本数据建立了预测模型,着重分析了精度要求对PSO-KPLS算法运行效率的影响。在以后的研究中,需要进一步分析教师科研绩效的主要影响因素,简化绩效模型,进一步设计高效的预测模型。2 教师科研绩效表示


3 实验仿真与分析

3.1 RMSE对寻优次数和运行时间的影响


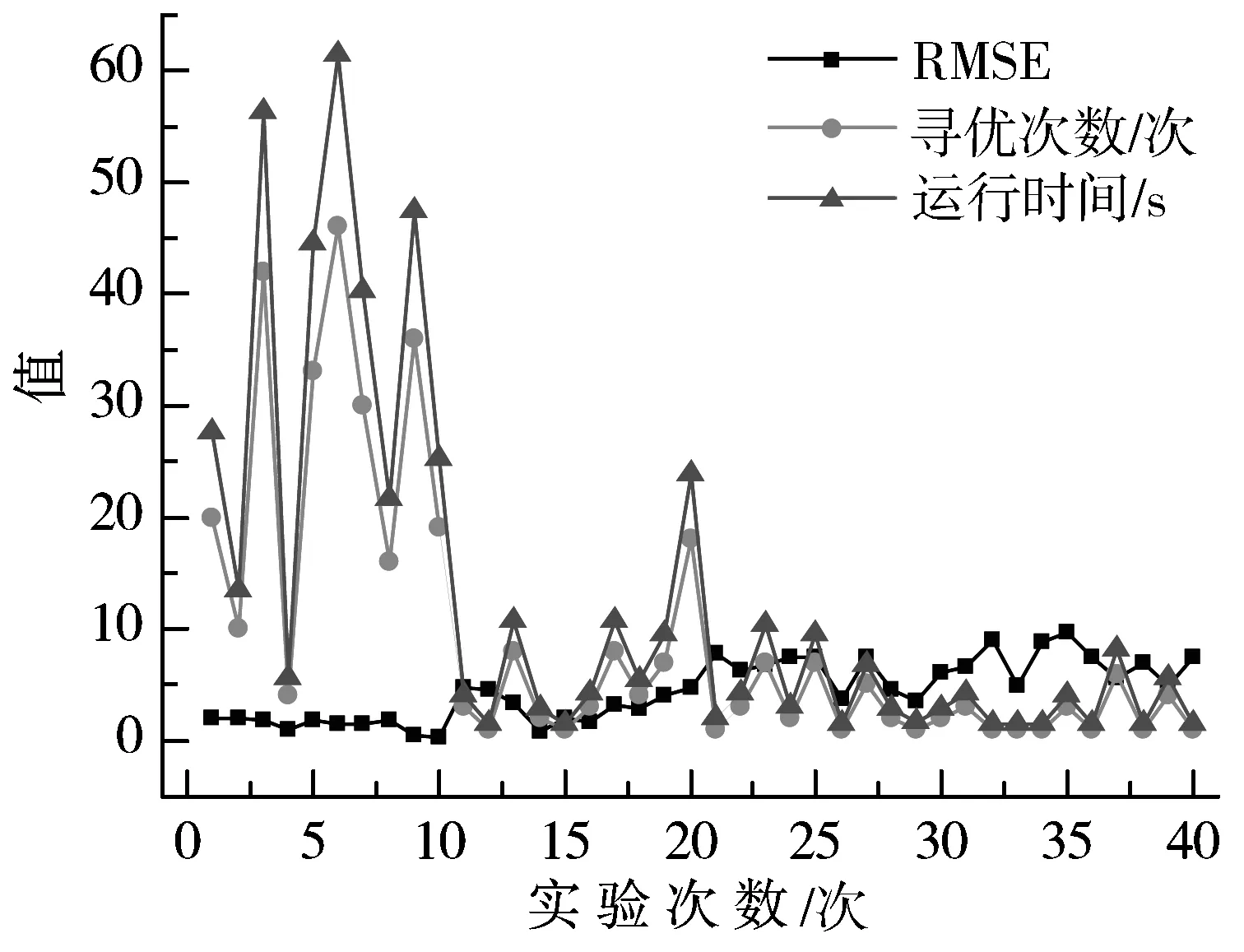
3.2 PSO-KPLS与其他改进的KPLS的性能对比

3.3 PSO-KPLS对部分科研绩效的预测结果

4 结束语
