基于向量分析法对麦克纳姆轮全向移动平台的研究

刘卓沄，卢桂萍，彭岗举

（1.北京理工大学珠海学院，广东珠海 519000；2.珠海华星智造科技有限公司，广东珠海 519000）

0 引言

随着机器人技术蓬勃发展，越来越多机器人竞赛出现。在大部分的机器人竞赛中，麦克纳姆轮全向移动平台已经得到了广泛运用，其所存在的数学分析是当今全向轮中的一个研究热点。国内外大多数对麦克纳姆轮运动分析以采用高等数学知识对其进行分析研究，存在分析复杂，理论性较强，应用性较低的情况。

本文将针对青少年在机器人竞赛中对无法运用所学知识理解麦克纳姆轮全向运动平台运动原理这一问题，通过向量分析法分析麦克纳姆轮的运动过程，利用数学分析建立全向平移运动学模型，使得青少年能够在机器人竞赛中予以实际运用麦克纳姆，提高青少年机器人竞赛的学术性，也可以提高青少年学生的创新实践能力和科学研究能力。

1 研究现状及背景

1.1 国内外研究现状

麦克纳姆轮是1973 年由瑞典Mecanum AB 公司工程师Bengtllon 提出，其承载能力大，运动性能优越，具有较高的研究价值。经过长期的发展，其相关设计制造技术已经较为成熟，而其相关运动学模型，正是当今研究的热点。由于麦克纳姆轮驱动的全向移动机器人存在诸多优势， 使其在工业界和学术界得到越来越多的关注，诸多学者对其运动学建模和动力学建模展开了研究[1]。

1.1.1 国外研究现状

Patrick Muir 使用矩阵变换的方法提出麦克纳姆轮全向移动平台的运动学模型。在国外Jorge通过对比传统车轮和全向轮的区别，并用旋量的方法提出麦克纳姆轮的运动学模型，王一治[2]讨论了麦克纳姆轮四轮系统实现全方位运动的条件，比较了常见的6种布局形式，进而优选出能实现全方位运动的最佳方案。Muir 等对此类机器人进行了运动学建模，从运动学方式上，给出了基于麦克纳姆轮的全向机器人运动学公式。Tlale 等为此类机器人建立了动力学模型并从动力学角度对基于麦克纳姆轮的全向机器人展开分析。尽管此类机器人的运动学和动力学模型发展较为成熟，针对应用于实际环境的移动机器人轨迹跟踪控制研究仍然方兴未艾[3]。

1.1.2 国内的研究现状

我国在移动机器人方面的研究起步较晚，但是发展势头却十分迅速[4]。目前国内大多数对麦克纳姆轮分析以采用高等数学知识对其进行分析研究，存在分析复杂，理论性较强，应用性较低的情况。

1.2 研究背景和设计目的及意义

麦克纳姆轮作为机器人竞赛中应用最广泛的全向平移平台，面向群体广。通过调查研究发现，不少青少年机器人赛事中，均出现了使用麦克纳姆轮作为竞赛的移动平台。而麦克纳姆轮存在结构繁琐，运动原理复杂，蕴含的理论数学知识较多的情况。但大多数青少年所掌握的数学理论知识，无法正确地运用在对麦克纳姆轮的分析中。

如何才能让青少年群体更加充分地理解麦克纳姆轮全向移动平台的运动原理是当下需要解决的一个问题。所以需要研究一种简单易懂的分析方法，使得青少年能够充分理解麦克纳姆轮的运动过程，正确使用麦克纳姆轮作为机器人的移动平台，并能通过简要的数学公式应用在机器人的运动控制中。提高青少年机器人竞赛的学术性，也可以提高青少年学生的创新实践能力和科学研究能力。

2 麦克纳姆轮全向移动平台设计

2.1 模型建立

麦克纳姆轮由一组围绕轮体对称放置的若干个全等小辊子组成，其中小辊子具备特殊轮廓曲线，具有零转半径的特点，能够在在平面内做任意方向的移动，从而实现机器人全方位移动的功能[5]。一个麦克纳姆轮需要由一个电机单独控制，并且4 个麦克纳姆轮所组成的全向移动平台具有良好的移动性能。因此，该研究选取两个左旋和两个右旋的麦克纳姆轮对称安装，组成全向移动平台，如图1～2所示。

图1 全向移动平台俯视图

图2 全向移动平台轴测图

2.2 与其他模型建立对比

从车体运动学方面，将别的分析方法设的众多物理变量里面一些对于理解麦克纳姆轮的运动平台影响不大的物理量省去，如别的分析方法设4个麦克纳姆轮的转动速度为ω1、ω2、ω3、ω4；车 体 的 速 度 为v1、v2、ω0；辊子的速度为vg1、vg2、vg3、vg4[3]。将辊子速度省去，把其他速度用向量进行表示，这样会更简洁易懂。在对单个麦克纳姆轮方面，同样地把辊子的运动曲线以及辊子的结构设计省去，因为此部分涉及的数学知识和力学知识比较多，青少年理解起来颇为困难，又因基于向量分析法对麦克纳姆轮全向移动平台的研究目的是为了让青少年更直观地理解麦克纳姆轮全向移动平台的运动原理，从而更有效地应用在比赛上。

3 麦克纳姆轮全向移动平台运动分析

3.1 对单个麦克纳姆轮分析

单个麦克纳姆轮的运动包括轮廓的运动和小辊子的运动。轮毂和不与地面接触的小辊子绕轮毂中心转动[6]。

如图3所示，左侧的麦克纳姆轮在地面上向前滚动时受到地面对轮子向前的摩擦力f，将这个力沿着滚轴的两个互相垂直的方向进行正交分解得到分力F1和F2，由于麦克纳姆轮四周的滚轴各拥有一个旋转自由度，所以分力F1实际上只使得滚轴转动而并没有影响轮子的移动；分力F2是对轮子有大小为fcos 45°的压力，那么轮子就会朝着F2的方向移动，这个分力才是让麦克纳姆轮移动的动力。同理，图3所示右侧的轮子会受到45°角斜向左上方的力。

图3 麦克纳姆轮受力分析

3.2 对麦克纳姆轮全向移动平台研究

单个麦克纳姆轮无法实现全方位移动，至少需要4个才能组成全方位移动平台。本文将以常规四轮麦克纳姆轮全向移动平台为例进行运动分析，该移动平台可实现全方位移动。

通过分析整体全方位移动平台，发现后两轮的情况和前两轮也是及其相似的，并得出以下结论：（1）左右一对麦克纳姆轮各自受到的力都斜向外侧呈45°夹角；（2）因为麦克纳姆轮全向移动平台中左上角的轮子安装和右下角的相同，右上角的和左下角的相同，所以在分析全向移动平台整体运动时可以把这两对相同特征的轮子整体考虑。

如图4～5 所示，以机器人的几何中心建立坐标系，原点C为车体的几何中心，其y轴始终指向车体纵轴，x轴与y轴垂直并组成右手坐标系，x轴与驱动电机输出轴平行，y轴与x轴垂直并组成右手坐标系。■→■■■CD表示麦克纳姆轮的右前轮和左后轮的单位速度，■→■■■CF表示左前轮和右后轮的单位速度，它们互相垂直，则可以把这两个矢量作为正交基底合成平面内任意一个矢量，这在机器人的移动上的效果则是改变4 个轮子的转速实现机器人在平地上的全向平移。

图4 全向移动平台坐标系

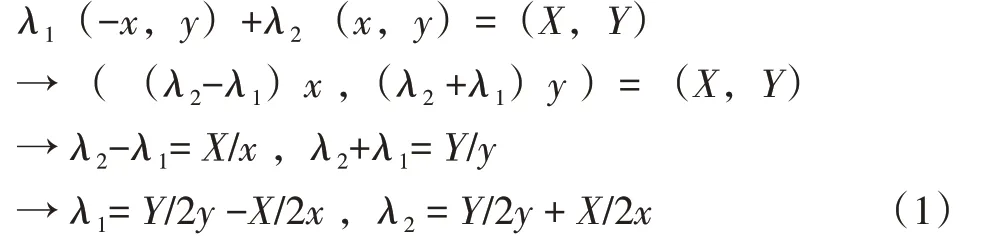
由图5得x和y的值为0.5，化简式（1）可得下式：

图5 全向移动底盘向量示意图

根据上述数学关系可知这两个实数可以分别表示两对安装相同的轮子的转速，因此可得出了麦克纳姆轮的全向平移运动模型如下：

4 应用实例

在青少年机器人竞赛中，机器人的运动控制尤为重要，在不少比赛中，对参赛选手所设计的机器人的移动精度提出了较高的要求。一项名为FTC 科技挑战赛的机器人竞赛，每年约有25 万名高中生参与其中，是规模最大的青少年机器人竞赛。该机器人竞赛分为自动阶段和手动阶段，在自动阶段，参赛机器人完全由事先编好的程序自动运行以完成指定任务。作为竞赛场地的环境设置较为复杂，故不可预见性较强。机器人能够在程序控制下完成任务，是靠自身安装的各种传感器“认识和感知”周围复杂的场地情况并自动判断执行相关程序。手动控制阶段， 则是参赛队员操控手柄， 通过WiFi 与机器人建立连接，手动控制机器人完成相关任务[7]。

4.1 全自动程序的应用

自动阶段需要让机器人全自主运动，在限定的时间内，完成对应的任务，这对机器人的移动提出了较高的要求。通过使用全向平移方程，只需用Y轴方向和X轴方向的位移计算出机器人所需位移的距离，根据麦克纳姆轮周出，以及每个轮子的转动圈数，再依靠时间与速度的关系计算出每个轮子分配的功率，即可以让机器人移动到指定的位置，避免了繁琐的程序编写，将全向移动平台自动控制代码由原来23 行命令代码，缩减到仅5行，实现了对程序的精简化，如图6所示。

图6 自动阶段程序

4.2 手动程序应用

手动阶段需要参赛选手通过遥控器操纵场上的机器人，完成相应的竞赛任务，需要更好地操纵机器人，尽可能做到人机结合。而参赛选手在场上所使用的遥控器由左右两个摇杆控制，摇杆的运动可分为x轴上的分量和y轴上的分量，且摇杆的返回值为x轴和y轴的坐标，将这特点与全向平移方程结合，能过完全模拟机器人的运动状态。降低了参赛选手对机器人的操作难度，提升了操作效率。如图7～8所示。

图7 手动阶段程序1

图8 手动阶段程序2

5 结束语

本文基于向量分析法对麦克纳姆轮全向移动平台的研究对麦克纳姆轮的应用，在研究方法上实现了创新，摈弃了难度较大的高等数学相关知识体系，能让青少年群体使用通俗易懂的知识体系进行研究，让青少年更好地运用自己的所学知识，提高综合运用知识能力和自学能力，具有一定的促进作用。并且可使得麦克纳姆轮更加广泛地运用在各种机器人竞赛乃至其他应用场合。

随着青少年机器人竞赛的普及，将会有更多的群体参与其中，更多难度较大的知识将会运用其中，未来将继续研究相关机器人竞赛的技术难点，普及相关机器人技术。