基于离散观测的随机系统非周期性间歇控制
2022-06-23汪海洋宋公飞
汪海洋, 宋公飞,2,3
(1.南京信息工程大学自动化学院,南京 210000; 2.华东理工大学能源化工过程智能制造教育部重点实验室,上海 200000; 3.江苏省大气环境与装备技术协同创新中心,南京 210000)
0 引言
随着人工智能的兴起,随机系统已被广泛应用于各种智能系统,所以随机系统的稳定性引起了人们广泛、密切的关注[1]。当随机系统中的系数不满足线性增长条件时,称其为非线性随机系统。文献[2]利用M矩阵理论,得到了一般非线性随机系统指数稳定性的一组条件,但是其控制器为连续时间控制器。在某些实际情况下,与连续时间控制器相比,基于离散时间观测设计的反馈控制器在精度和速率方面具有突出的优势[3-6]。文献[7]利用基于离散时间观测的反馈控制,研究了非线性混合随机系统的均方指数稳定性。但需要指出的是,上述文献中所提出的随机稳定都是基于经典反馈控制器。近年来,间歇性控制器越来越受到关注[8-14],它将时间分为工作时间和休息时间两部分。控制器工作时间工作,休息时间关闭,并以这种方式来回切换。与传统的反馈控制器相比,间歇控制器可以有效地延长控制器的工作寿命。并且,非周期性间歇控制器在提高控制精度和降低工作成本方面更为出色。文献[15]提出了一种基于离散时间状态观测的非周期间歇控制方法使得神经网络系统达到指数同步;文献[16]针对受控系统的扰动提出了基于离散时间观测的间歇控制方法,使得系统达到随机稳定。但都没有通过离散观测的间歇控制方法针对随机系统设计控制器使其稳定,关于这一主题的文献也很少。
本文设计基于离散观测的非周期性间歇控制器使得随机系统的指数稳定,并且利用Lyapunov函数方法严格证明了在离散观测的非周期性间歇控制下系统指数稳定的判据条件。
1 模型描述与预备知识
1.1 模型描述
考虑一个非线性随机系统,其形式为
dx(t)=F(x(t),t,r(t))dt+G(x(t),t,r(t))dw(t)t≥t0
(1)
式中:x(t)∈Rn,表示系统状态;r(t)表示一个马尔可夫链,在有限空间S={1,2,…,N}中取值;F∶Rn×R+×S→Rn和G∶Rn×R+×S→Rn×m,表示连续的非线性函数;w(t)∈Rn,表示标量布朗运动;t0为初始时间。为了使这个不稳定的随机系统变得稳定,考虑加上一个基于离散时间观测的非周期性间歇控制器,则形式变成
dx(t)=[F(x(t),t,r(t))+U(x(δ(t)),t,r(t))]dt+
G(x(t),t,r(t))dw(t)t≥t0
(2)
控制器U(x(δ(t)),t,r(t))的形式为
(3)
式中:Ki表示控制增益矩阵;x(δ(t))=x([t/τ]τ),表示离散观测,τ>0,表示两次连续观测之间的持续时间,[t/τ]表示t/τ的整数部分;ti,ti+1为相邻2个控制周期的起始时刻;si为相邻控制起始时刻的时间间隔,根据系统的状态决定。
1.2 预备知识
假设1 存在两个正实数h1,h2,使得
|F(x,i,t)-F(y,i,t)|≤h1|x-y|
(4)
|G(x,i,t)-G(y,i,t)|≤h2|x-y|
(5)
其中,(x,y,i,t)∈Rn×Rn×S×R+,并且有F(0,i,t)=0,G(0,i,t)=0。
假设2 存在两个正标量α,β且0≤α≤β,则有
(6)
假设3 对于每个i∈{1,2,…,n},∀x∈R有
(7)
tr[G(t,r(t),x(t))TVxx(t,r(t),x(t))G(t,r(t),x(t))]≤

(8)

(9)
成立。
证明 假设t∈[vτ,(v+1)τ),其中v≥0,令δ(t)=vτ,则有
x(t)-x(δ(t))=x(t)-x(vτ)=
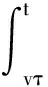
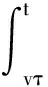
(10)
E|x(t)-x(δ(t))|2≤


[6τ(τH1+H2)+3τ2Hk]E|x(vτ)|2
(11)
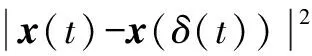
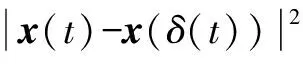
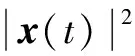
(12)
从而可知对于引理1的证明是完整的。
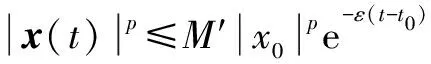
2 指数稳定性
通过Lyapunov理论的分析方法,得到式(1)系统在满足指数稳定性时的条件。

证明 选取Lyapunov函数V(x(t),t,r(t))=xT(t)·x(t),当t∈(ti,si]时,
dV(x(t),r(t))=LV(x(t),r(t))dt+dM(t)
(13)
其中M(t)表示一个鞅且M(0)=0。
LV(x(t),t,r(t))=
2xT(t)[F(x(t),t,r(t))+Kix(δ(t))]+
tr[G(x(t),t,r(t))TVxx(t,r(t),x(t))G(x(t),t,r(t))]+
(14)
根据假设1、假设2得

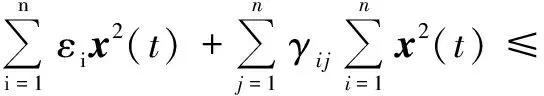
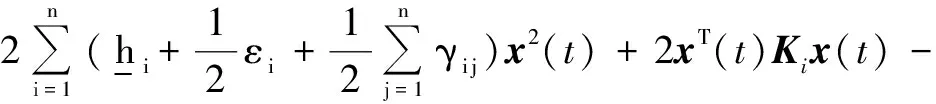
2xT(t)Ki(x(t)-x(δ(t)))≤

2xT(t)Ki(x(t)-x(δ(t)))≤
η1x2(t)-2xT(t)Ki(x(t)-x(δ(t)))
(15)
根据广义伊藤公式
eθ tV(x(t),t,r(t))=eθ t0V(x(t0),t0,r(t0))+

(16)
将式(15)代入式(16)得
eθ tEV(x(t),t,r(t))≤eθ t0EV(x(t0),t0,r(t0))+

x(δ(s))|)ds
(17)
2KiE(|x(s)||x(s)-x(δ(s))|)≤
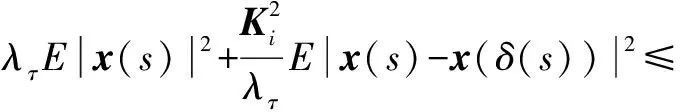


(18)
综上,有
eθ tEV(x(t),t,r(t))≤eθ t0EV(x(t0),t0,r(t0))+
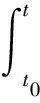
(19)
再令θ=2λτ-η1,可得θ+η1-2λτ=0,则
E[eθ tV(x(t),t,r(t))]≤E[eθ t0V(x(t0),t0,r(t0))]
(20)
用类似的方法,当t∈(s0,t1]时,
eθ tV(x(t),t,r(t))=eθ s0V(x(s0),s0,r(s0)+
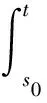
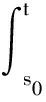
(21)
等式两边同取期望,则有
E[eθ tV(x(t),t,r(t))]≤E[eθ s0V(x(s0),s0,r(s0))]+
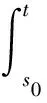
(22)
对式(22)使用Gronwall不等式,得到
E[eθ tV(x(t),t,r(t))]≤
E[eθ s0V(x(s0),s0,r(s0))e(θ+η2)(t-s0)]
(23)
根据式(23)可得
E[eθ s0V(x(s0),s0,r(s0))]e(θ+η2)(t-s0)≤
E[eθ t0V(x(t0),t0,r(t0))e(θ+η2)(t-s0)]
(24)
所以,就有当t∈(s0,t1]时,
E[eθ tV(x(t),t,r(t))]≤
E[eθ s0V(x(s0),s0,r(s0))]e(θ+η2)(t-s0)≤
E[eθ t0V(x(t0),t0,r(t0))]e(θ+b2)(t-s0)
(25)
同样,当t∈(t1,s1]时,
E[eθ tV(x(t),t,r(t))]≤
E[eθ s0V(x(t1),t1,r(t1))]≤
E[eθ t0V(x(t0),t0,r(t0))e(θ+η2)(t1-s0)]
(26)
当t∈(s1,t2]时,
E[eθ tV(x(t),t,r(t))]≤
E[eθ s1V(x(s1),s1,r(s1))]e(θ+η2)(t-s1)≤
E[eθ t0V(x(t0),t0,r(t0))]e(θ+η2)(t1-s0)+(θ+η2)(t-s1)
(27)
重复类似的过程,对于任何t∈(ti,si],i=1,2,…,都有
E[eθ tV(x(t),t,r(t))]≤
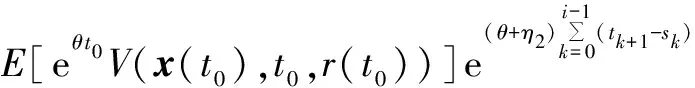
(28)
对于任何t∈(si,ti],i=1,2,…,则有
E[eθ tV(x(t),t,r(t))]≤
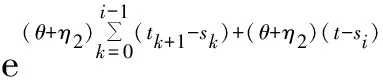
(29)
因此,得到
E[eθ tV(x(t),t,r(t))]≤

(30)
且有
EV(x(t),t,r(t))≤

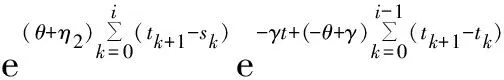
(31)
根据定义1,可以得到
E|x(t)|2≤
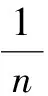
(32)
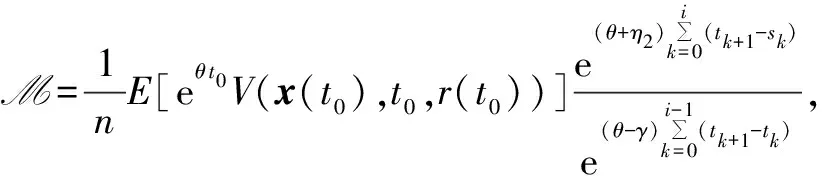
E|x(t)|2≤Me-γt
(33)
由此可得,式(1)的随机系统是均方指数稳定的。定理1 证毕。
当si-ti=α和ti+1-ti=β时,该控制就被称为周期性间歇控制。然后,可以有如下推导结果。
推论1 在前面所提假设满足的情况下,有
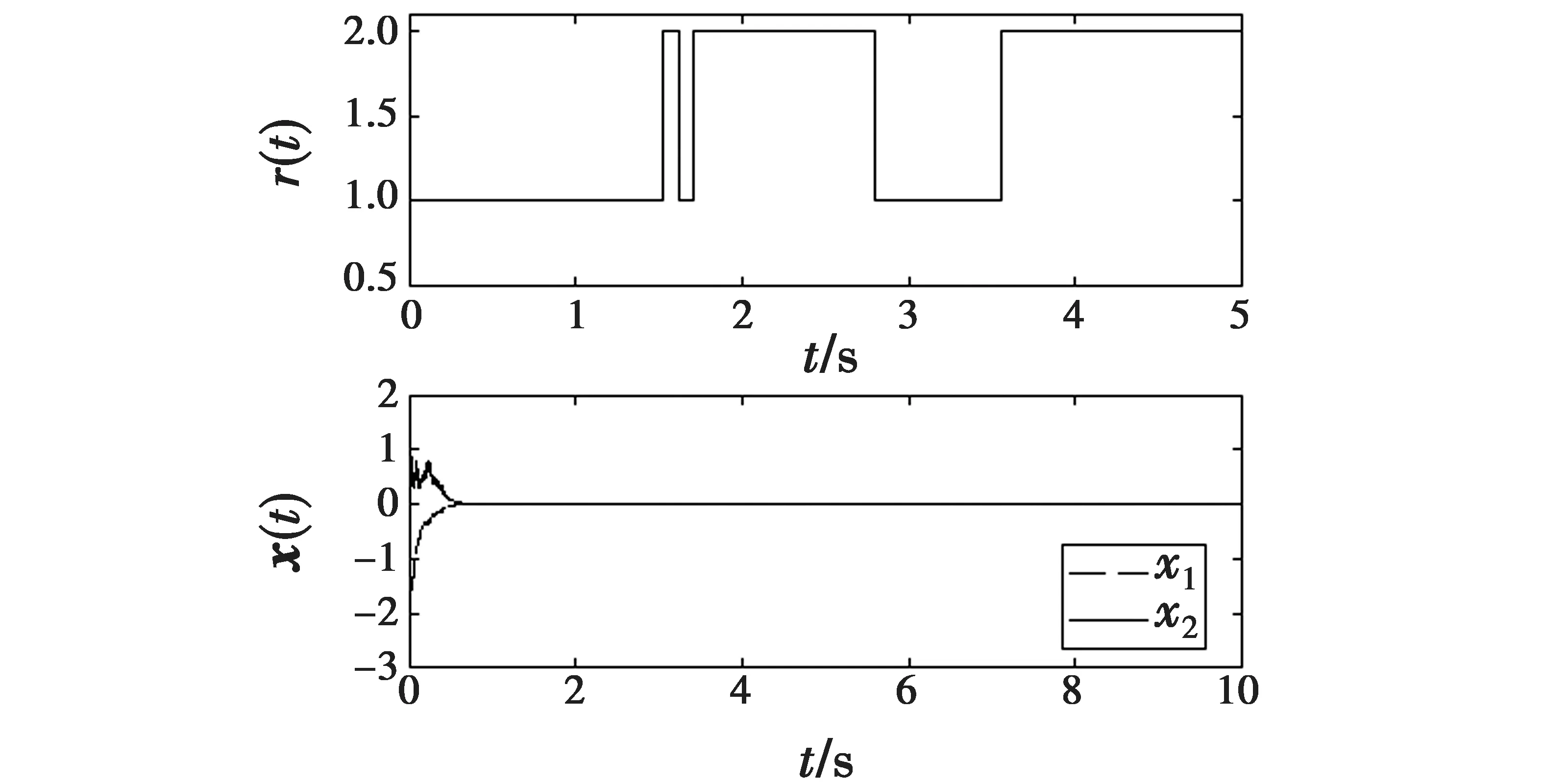
e(θ+η2)(β-α) (34) 这意味着式(2)通过基于离散观测的周期性间歇控制在均方数上呈指数稳定。 通过数值模拟来证明所得到的非周期性间歇控制器的有效性,考虑一个混合非线性随机系统有如下形式 dx(t)=A(r(t))x(t)dt+B(r(t))x(t)dw(t)t≥t0 (35) 设置初值r(0)=1,x1(0)=-2,x2(0)=1。通过软件仿真可得此时式(1)系统是不稳定的,仿真如图1所示。 图1 无非周期性间歇控制器的随机系统状态响应 为使式(1)系统保持稳定,设计基于离散观测的非周期性间歇控制器,形式如式(3)所示,设置控制增益为-10,非周期性间歇控制器参数为α=0.3和β=0.5。通过定理1计算,令τ=0.000 01,加入控制器后,经过软件仿真可得系统是均方指数稳定的,结果如图2所示。 图2 离散观测非周期性间歇控制器的随机系统状态响应 本文利用基于离散观测的非周期性间歇控制方法研究了混合随机系统的指数稳定问题。根据Lyapunov稳定理论,利用适当的离散观测非周期性间歇控制律,导出了保证不稳定混合随机系统指数稳定的判据条件。另外,通过在控制函数中替换适当的值,再根据已设定的条件推导出基于离散观测周期性间歇控制的稳定问题。最后,通过数值模拟验证了该控制方法的有效性。鉴于不连续控制器在工程实际中应用领域广泛,相信基于离散观测的非周期性间歇控制法可成为随机系统控制或同步的一种新颖而有效的方法。3 数值仿真
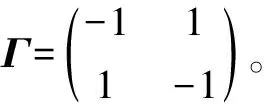

4 结束语
