储能电池辅助火力发电机组二次调频建模研究

张雨萌，许传龙，齐 琪，张 彪，李 健

(东南大学火电机组振动国家工程研究中心，能源与环境学院，江苏 南京 210096)

0 引言

随着风能、太阳能等新能源装机容量的迅猛增长，以新能源为主体的新型电力系统已成为我国电力发展的必然趋势。但新能源发电系统出力具有波动性和不确定性，会造成功率和频率的剧烈波动，给频率调节带来巨大挑战。机组调节频率的方式主要是一次调频和二次调频。一次调频是有差调节，要实现无差调节需要依靠二次调频，即发电厂机组根据电网调度中心下发的调度指令，增减机组功率，利用调频器来恢复频率的过程[1]。

火电机组作为传统调频电源在调频过程中存在超调、欠调、延迟调节等问题，难以满足新型电力系统的要求。而电化学储能具有响应快速、能量密度高等优点[2]，成为一种新型辅助调频手段受到关注。研究表明，传统火电机组适合于大幅度、单向的负荷调度[3]，而电化学储能化学能和电能的转换在瞬间完成，可以精确调节小幅度负荷信号。因此将储能电池与火力发电机组相耦合，不仅可以改善火电机组频繁调整出力造成的磨损，还可以更精准地跟踪AGC(Automatic Generation Control，AGC)指令。

火力发电机组和电池储能系统的负荷控制模型是研究两者调频过程中负荷分配、优化协调控制的基础。从调频主体的角度来看，火电机组调频过程涉及到协调控制系统(Coordination Control System，CCS)、汽轮机及其调速器、锅炉和发电机四部分，但是目前主要研究集中在储能辅助电网侧调频的模型构建上，过度简化火电机组模型，默认锅炉是个无限快速能源供体，单从阀门开度的角度反映功率，如文献[4]在建模时忽略了CCS和锅炉。文献[5-6]将火电机组简化为调速器和原动机两部分，研究储能参与电网调频的控制策略。但汽轮机出力同时受到锅炉主蒸汽压力的影响，因此有必要对火电机组二次调频的过程机理进行系统分析，并建立考虑主蒸汽压力的负荷控制模型。

锂电池因充放电速度快、转换效率高等优点成为化学储能技术的研究重点。目前锂电池模型主要有等效电路模型和电化学模型，其中等效电路模型忽略电池内部物理化学特性，容易在工程上实现。锂离子电池等效模型主要有一阶RC模型、戴维南模型、二阶RC模型等[7]。但是研究中多使用简化模型，如文献[8]提出用一阶惯性环节来描述电池参与调频时的动态特性。文献[9]使用简化惯性模型进行储能参与调频的控制策略研究。一阶惯性模型不仅不能精确描述电池动态特性，而且也无法获知运行过程中电池的状态，而二阶RC模型结构较复杂，能够更精确地描述锂电池高倍率放电时的极化状态，更适用于实际调频过程仿真。

本文主要开展了发电侧储能电池辅助火电机组二次调频的建模研究。首先基于机理建模方法构建了包含CCS、锅炉等子系统的火电机组模型，同时构建基于二阶RC等效电路模型的电池模型。进一步构建了发电侧储能电池辅助火电机组二次调频的模型，并且在Matlab/Simulink中进行了阶跃仿真和正弦波仿真，以验证模型的有效性。

1 火电机组负荷控制模型

火电机组负荷控制模型主要包括协调控制系统、汽轮机及其调速器、锅炉和发电机四个子系统。协调控制系统包括汽轮机主控制器、锅炉主控制器和负荷指令处理环节。图1中Pe为发电机电磁功率，PM为汽轮机输出功率，TD为汽轮机阀门开度指令，BD为锅炉燃烧指令，CV为汽轮机阀门开度，PT0为设置的主蒸汽压力值，PT为实际的主蒸汽压力值，ms为蒸汽流量，Δω为机组转速偏差。

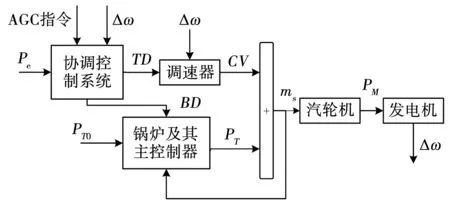
图1 火电机组调频模型

当电网负荷产生波动时，整个系统形成一条动态变化的链，机组转速产生偏差，锅炉主控制器发出锅炉燃烧指令，引起锅炉燃烧率的变化，进而导致锅炉主蒸汽压力的变化，为了维持汽轮机压力恒定，必须使汽轮机蒸汽流量的阀门开度随之变化，继而汽轮机的机械出力改变，送入电网的负荷改变，整个系统形成反馈环节，达到协调控制的目的。

本文采用机理建模的方式构建容量为660 MW的火电机组调频模型，下面将从锅炉及其主控制器、汽轮机主控制器及调速器、汽轮机模型结构进行详细描述，模型的参数选取参考文献[10-12]。

1.1 锅炉及其主控制器模型

直流锅炉没有汽包，给水依次经过加热区、蒸发区、过热区，把过热蒸汽送入汽轮机做功。该过程的储能特性由通过等效节流孔连接的蒸发蓄能和过热蓄能两个集总储能环节表征[13]。图2为锅炉及其主控制器模型，模型中的主要参数见表1。

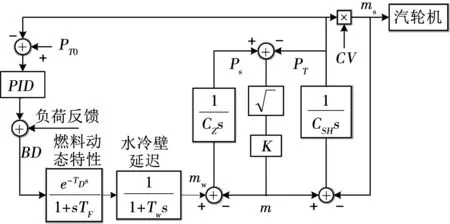
图2 锅炉及其主控制器模型

表1 锅炉模型参数

1.2 汽轮机主控制器及调速器模型

机组负荷指令是AGC指令和发电机转速偏差的代数和，汽轮机主控制器以机组负荷指令和电网功率之差作为输入信号，经过PID调节后输出汽轮机阀门开度指令TD，TD指令送至汽轮机数电液调速系统(Digital Electric-hydraulic Control System，DEH)，最终输出阀门开度信号CV。图3为汽轮机主控制器及调速器模型，模型中的主要参数见表2。

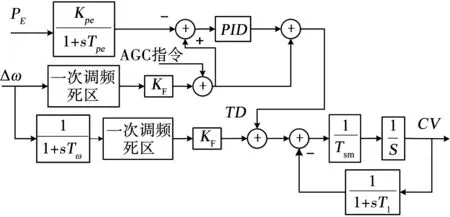
图3 汽轮机主控制器及调速器模型

表2 汽轮机主控制器及调速器参数

1.3 汽轮机模型

图4为汽轮机模型。本文选取的模型是文献[9]中的改进汽轮机模型。该模型在IEEE经典汽轮机模型的基础上加入了高压缸、中压缸过调系数，仿真证明该模型为汽轮机出力动态过程中的过调现象。模型中的主要参数见表3。

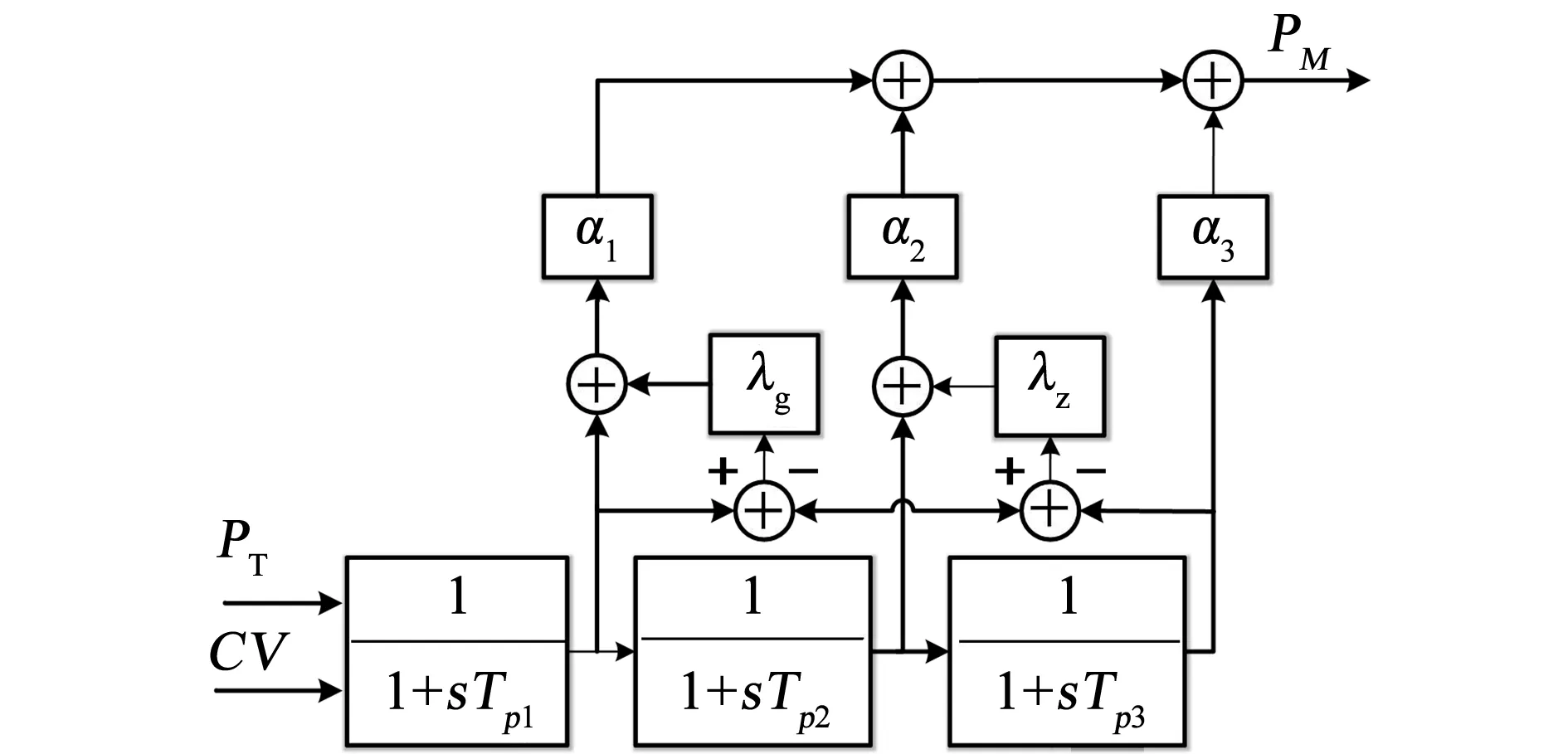
图4 汽轮机模型

表3 汽轮机模型参数

1.4 模型仿真与验证

为了验证所建立模型的合理性，将上述各子系统相互连接，在Matlab/Simulink中搭建火电机组二次调频动态模型，进行了仿真验证。将系统以额定频率50 Hz和机组容量660 MW为基准值进行标幺化，为系统接入模拟的AGC阶跃性信号，考虑到火电机组爬坡速率的限制，对输入信号预处理，限速3%Pn/min。仿真结果如图5所示。仿真时间1 900 s，前1 100 s保持0.75 pu输入使系统达到稳定状态。从图中可以看出，所建火电机组模型的出力趋势与AGC指令变化趋势相符，但是火电机组参与调频时存在延迟、超调、欠调等问题，调频效果有待改进。

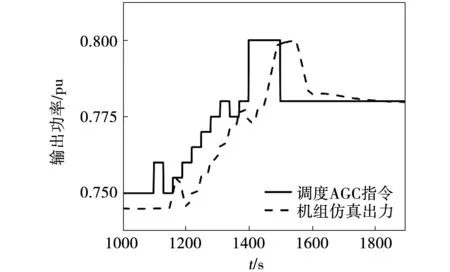
图5 火电机组AGC指令响应曲线

2 储能电池等效电路模型

等效电路模型通过电器元件不同组合方式来描述电池的充放电特性[14]，并通过参数辨识识别未知参数，实现电池模块的仿真。

2.1 模型构建及参数辨识

二阶RC模型是包含两个电阻电容并联网络的电池等效电路模型，其结构如图6所示。其中Uoc是电池的开路电压，U是电池端电压，I是干路电流，三者之间的关系可表示为

图6 锂电池二阶RC等效电路模型

(1)

参数辨识时会出现数据饱和，随着迭代次数增加，估计值和真实值的偏差会越来越大。限定记忆最小二乘法的原理是辨识所使用的数据长度不变，增加一个新数据的同时去掉一个旧数据，常使用的遗忘因子算法虽然在不断削弱老数据的权重，但是不管多老的数据都在起作用，而限定记忆法克服了这种缺陷，可以更有效解决数据饱和问题。

首先得到式(1)的离散化方程

(2)

令

(3)

可得模型参数

(4)

使用混合脉冲功率特性(Hybrid Pulse Power Characterization，HPPC)测试进行电池参数辨识，已知U(k)、I(k)、SOC(k)，根据拟合出的Uoc和SOC的关系可得Uoc(k)，求解k1～k5。定义参数矩阵C和变量矩阵H

(5)

定义记忆长度L=2 200，P矩阵用来存放方差，每增加一组观测数据H(k+L)，根据最小二乘递推算法可得第(k+L)时刻的方程

(6)

每增加一组新数据的信息，就要去除一组老数据的信息

(7)

最终得到k1～k5，根据式(4)求得各个参数的值，结果如表4所示。可以看出SOC在20%～80%范围内各个参数值变化较小。

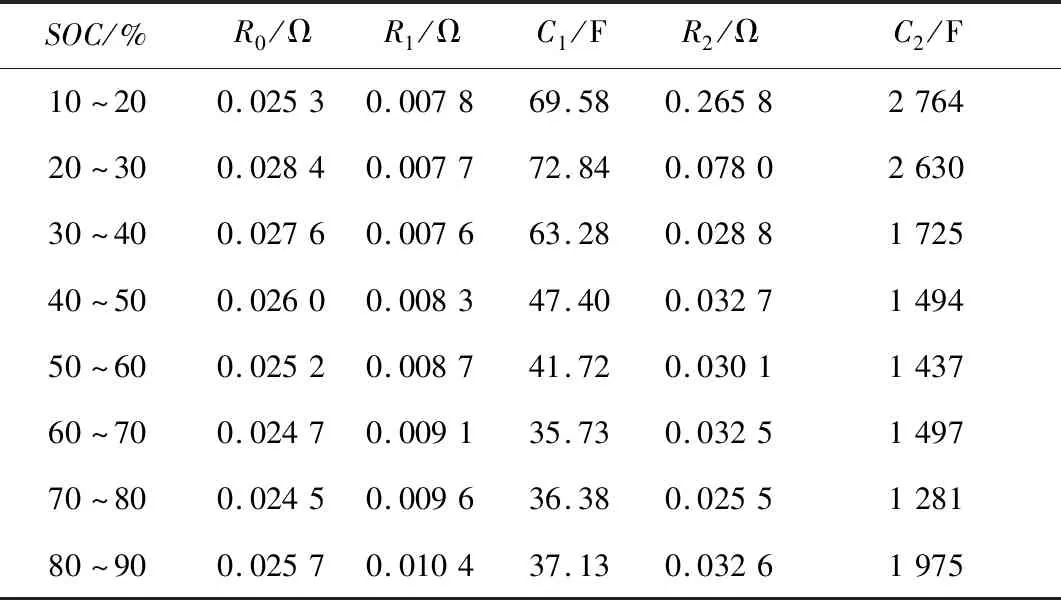
表4 参数辨识结果

2.2 仿真验证

本节对上述参数辨识结果进行验证。首先定义式(8)为平均相对误差评价参数辨识结果

(8)

式中U*(i)和U(i)——第i个时刻的实验电压值和仿真电压值。

只计算SOC在20%～80%范围内的误差值。选取SOC=50%时辨识出的参数值代入模型，以相同的脉冲电流作为输入，端电压作为输出，与实验值进行对比，结果如图7所示。实验电压和仿真电压的相对误差仅为0.052 4%，精确度较高。

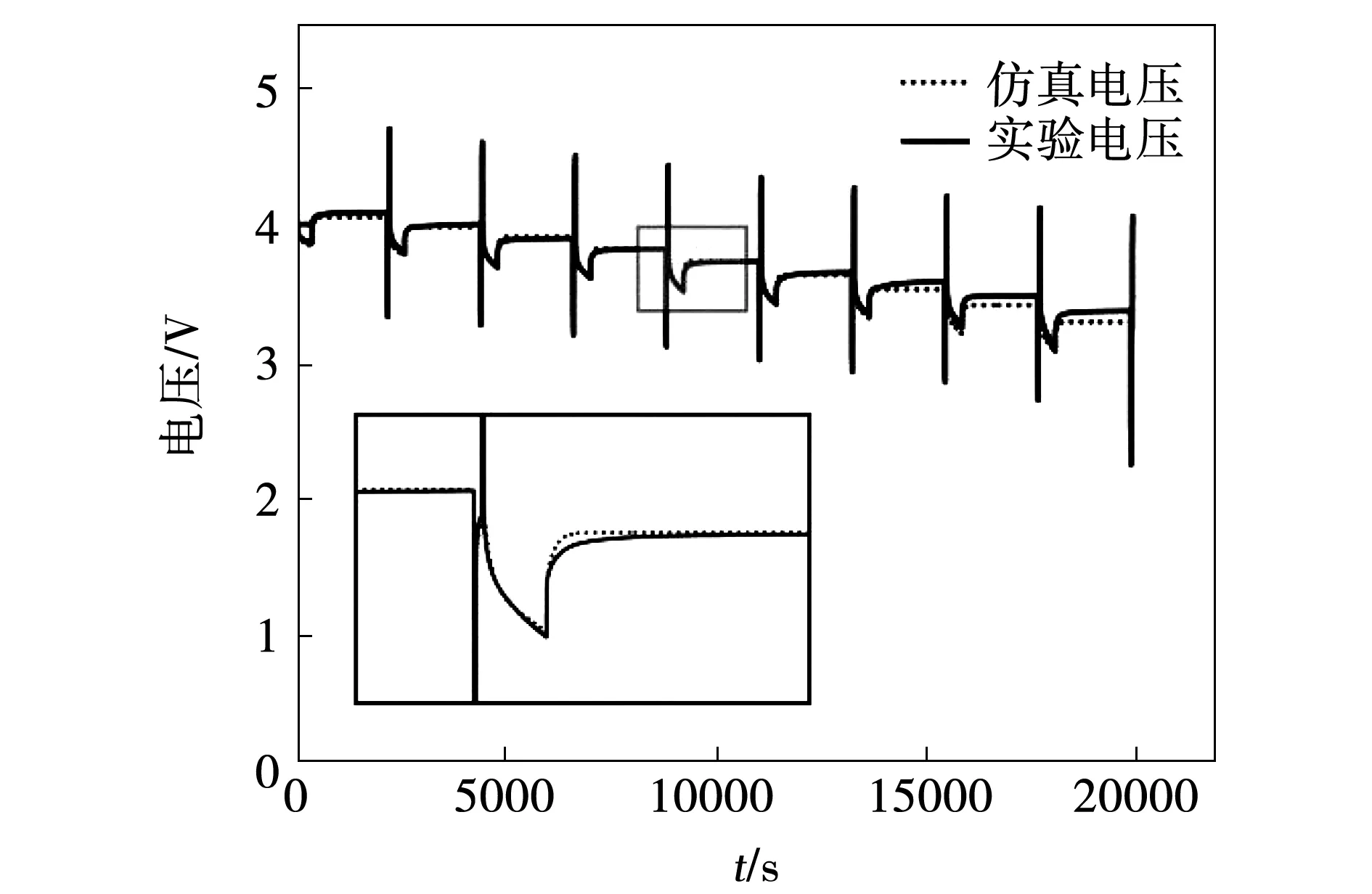
图7 实验电压与仿真电压对比曲线

将阶跃性AGC指令以储能功率为基准值进行标幺化，由储能单独完成二次调频，结果如图8所示。储能电池出力与AGC指令曲线几乎完全重合，由此可见，锂电池的调频效果优于火电机组，储能辅助二次调频是具备合理性的。

图8 储能电池AGC指令响应曲线

3 电池储能辅助火电机组调频模型与仿真

储能辅助火电机组二次调频的系统框架如图9所示。具体过程为：当电网频率产生偏差后，调度中心给火电厂下发AGC指令，送入远程测控终端，总控系统将AGC指令等运算数据经过计算后分配给火电机组协调控制系统和储能控制系统，机组和储能系统同时参与二次调频，最终将出力合并上传电网，作为考核依据。储能系统的加入不会改变原有机组的控制方式和AGC调频效果[15]。

图9 储能辅助二次调频系统框图

将所建立的火电机组模型与储能模型耦合起来，储能电池配置容量为40MW。首先进行阶跃仿真验证，火电机组和储能系统按照比例分配AGC指令，结果如图10(a)所示，可以看出加入储能环节后，功率波动的幅度减小，超调量由34.98%下降到19.62%，欠调量由35.5%下降到24.73%，最终达到目标调节值的时间由1 155 s缩短到970 s，并且储能系统可以做到立刻响应，改善火电机组的延迟动作问题。

然后进行正弦波仿真验证，AGC指令由波形Ⅰ(幅度0.03 pu，频率0.1 pu)和波形Ⅱ(幅度0.2 pu，频率0.004 pu)叠加形成。根据各自的调节特点，由储能系统调节波形Ⅰ，火电机组调节波形Ⅱ，结果如图10(b)所示。对于小幅度高频的信号，由于爬坡速率的限制，火电机组无法做到精确调节，但是储能系统可以更快速、更精准地完成二次调频任务，同时避免火电机组频繁启停。

图10 耦合模型不同指令下的响应曲线

4 结论

本文将AGC指令直接作为系统的输入，分别建立了火电机组考虑主蒸汽压力的系统模型和储能电池等效系统模型。在此基础上，建立了储能电池辅助火力发电机组二次调频耦合模型，并进行阶跃仿真和正弦仿真验证。仿真结果表明：

(1)火电机组模型响应AGC指令时存在超调、欠调等问题，调频效果有待改善;

(2)电池模型电压相对误差仅为0.052 4%，模型可以更精确地描述二次调频过程中的动态特性;

(3)储能电池辅助二次调频模型可以减小超调量、提升响应速度、缩短调节时间，从而改善火电机组的调频效果。

本文虽然建立了锂电池辅助二次调频的动态模型，但是并没有分析实际的AGC指令，也忽视了电池的寿命情况，今后的研究重点可放在调频运行策略和电池状态预测上。