基于线性位移模式的环形谐振子理论研究

裴永乐，高立民，徐 亮，李 华，李晓辉，李录贤

(1.中国科学院西安光学精密机械研究所，西安 710119；2.西安交通大学航天航空学院，机械结构强度与振动国家重点实验室,飞行器环境与控制陕西省重点实验室，西安 710049)

0 引言

谐振陀螺又称为固体波动陀螺，是一种利用谐振子的驻波进动效应测量基座旋转的无转子式陀螺仪。由于其结构简单、精度高、体积小、能耗小、工作温度范围大等显著优点，被广泛应用于航空、航天、航海、地面定位等领域。经典的谐振陀螺主要包括谐振子、基座以及激励组件等部件(有些也可将基座与激励组件整合在一起)，如图1所示。其中，谐振子是谐振陀螺的敏感部件，也是谐振陀螺的核心部件，通常情况下，谐振子有两种典型结构类型：简化环型和旋转薄壳型(如半球谐振子、钟形谐振子等)。由于环形谐振子与旋转薄壳型谐振子具有相同的四波腹振型和相似的动力学特性，可以用环形谐振子的模型来简化研究半球谐振子唇缘的动态特性。

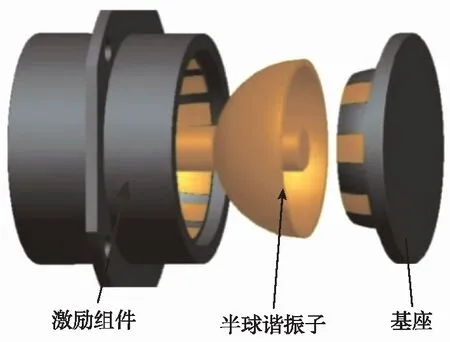
图1 谐振陀螺结构示意图

经典的环形谐振子理论是基于弹性力学理论以及几何中性轴(或称中心线)不可拉伸假设建立的(见式(1)之二式)。如图2所示，对于环形结构，建立极坐标系-，和分别为环形结构几何中心线(中性轴)的曲率半径和特征长度，挠度(,)的控制方程及相关约束条件为

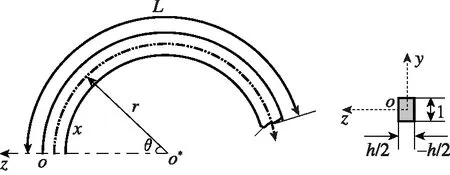
图2 环形结构及坐标系示意图

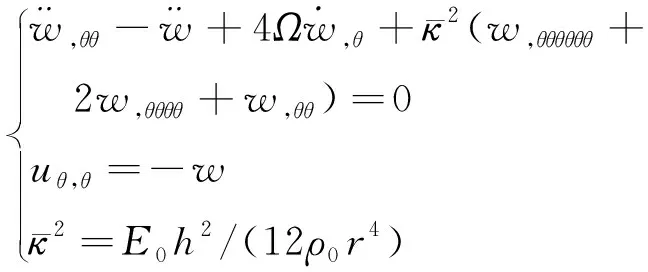
(1)

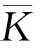
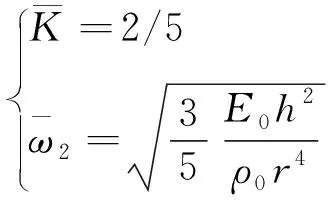
(2)

然而，在目前经典环形谐振子理论中,仍存在许多不足之处：1)经典理论对应的挠度控制方程式不能精确描述环形结构的静态弯曲问题；2)对于动态响应问题，基于经典理论获得的理论解式(2)不能精确反映结构特征尺寸(如高度、曲率半径等)对动态响应的影响规律(特别是进动系数和二阶振动角频率)；3)经典理论也未充分考虑环形结构上、下表面剪应力自由条件。

因此，为了克服上述不足，本文从环形结构的基本假设和基本条件出发，系统地开展环形谐振子结构静、动态问题的理论研究。

1 环形结构问题的数学描述

根据文献[9-10]，建立坐标系-，如图2所示。对于一个环形结构问题，可近似看成是一个平面应力问题。因而，三维弹性理论中6个应力分量减少到3个(即、和)；3个独立的位移分量减少到2个(即和)。对于环结构问题，通常还进一步采用如下2个广义位移定义以及基本概念。

1.1 广义位移的定义

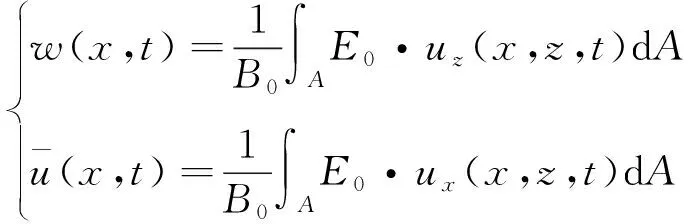
(3)

其中，表示环横截面的面积;为环截面的拉伸刚度，其含义为

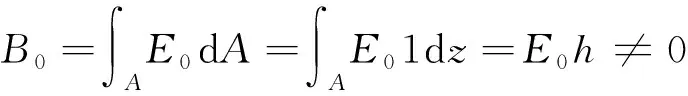
(4)

1.2 基本概念和基本假设

对于环结构问题，通常还进一步采用如下2个基本假设和1个基本条件。

基本假设1：径向正应力相对和较小，因而在环结构中忽略不计(即=0)；其余2个应力与应变之间满足退化的胡克(Hooke)定律，即

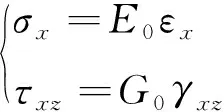
(5)

其中，和分别为截面上的正应变和剪应变；及分别表示材料的弹性模量和剪切模量，进而几何关系可以表示为

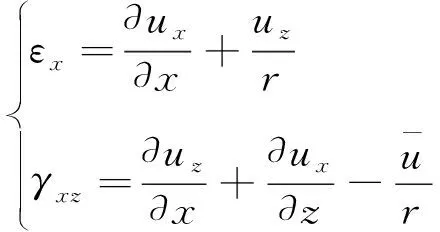
(6)

基本假设2：径向正应变恒等于零，即

=0

(7)

其含义为

∂∂=0

(8)

式(8)表明,径向位移只是的函数，不随着高度坐标发生变化。

基本条件1：上、下表面剪应力自由条件。

根据基本假设1中式之二式，剪应力自由条件等价于

(,±2,)=0

(9)

1.3 位移模式及本构关系

对于环形结构，假设其位移模式为以下线性形式

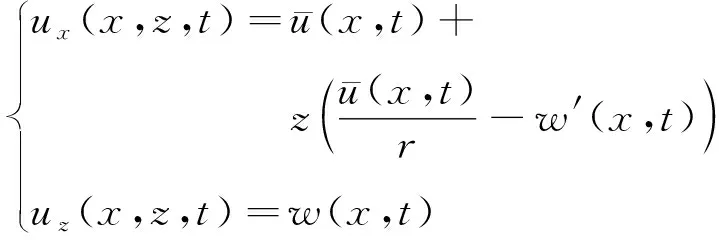
(10)

其中，“′”表示物理量对周向坐标的一阶偏导数。显然，上述位移模式满足式(9)(即上、下表面剪应力自由条件)。将式(10)代入几何关系式(6)可得

(11)

对于环结构问题，其广义应力的定义如下

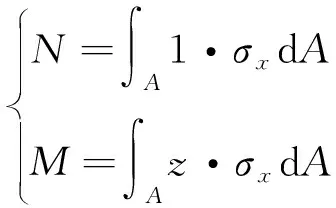
(12)

其中，和分别为周向拉力和弯矩。

根据本构关系式(5)和几何关系式(11)，可得环结构的广义本构关系为

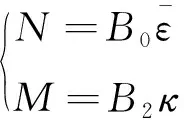
(13)

并且

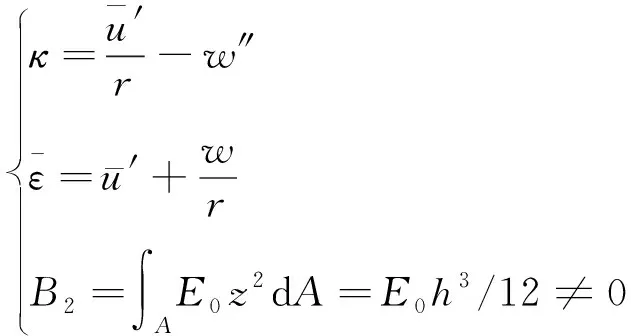
(14)

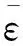
2 环形结构的静态弯曲问题

弯曲问题是环形结构静力学的基本问题，目前已有许多学者进行了系统的研究，但是仍然没有获得精度很高、形式简单的解析解。因此，这一节重点研究圆环结构的静态弯曲问题。

2.1 静态弯曲问题的基本理论

根据环结构的虚功原理，可得

0=δ+δ

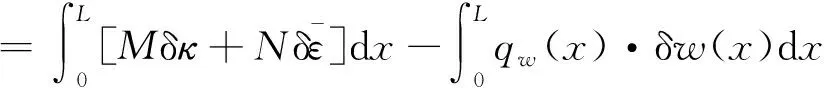
(15)

其中，()为几何中心线上的载荷分布函数。

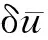
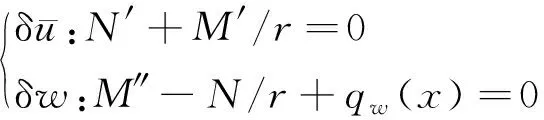
(16)

将式(13)和式(14)代入式(16)，平衡方程为

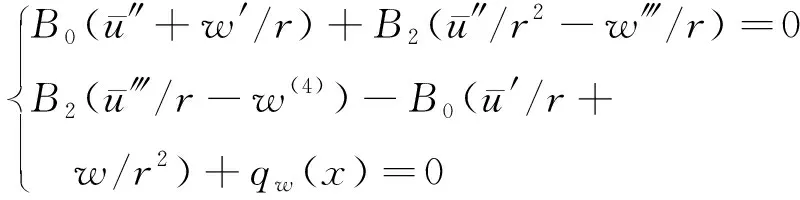
(17)

相应的边界条件为

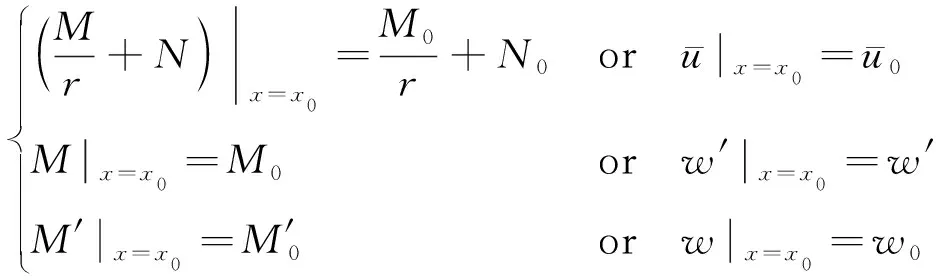
(18)

当对于整个圆环结构进行分析时，取=2π，此外，还需要充分考虑环结构的连续性条件(或周期性条件)，从而保证计算结果的准确性。从环结构的物理意义上讲，环结构的连续性条件可表述为

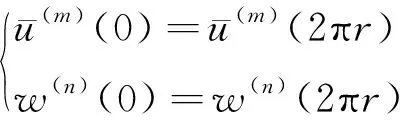
(19)

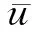
2.2 静态弯曲问题的理论解

对于环结构弯曲问题，根据式(13)、式(14)和式(16)，有

″+=()

(20)

即

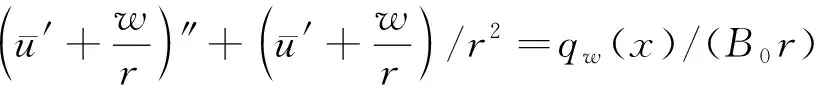
(21)

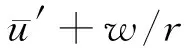
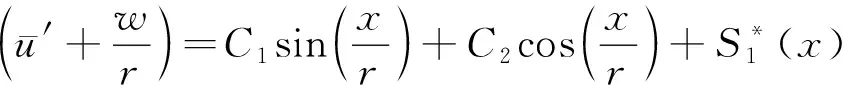
(22)

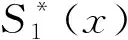
根据式(16)中第一式，可得

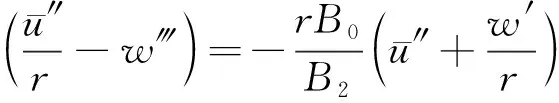
(23)

根据式(22)和式(23)，消去变量()可得

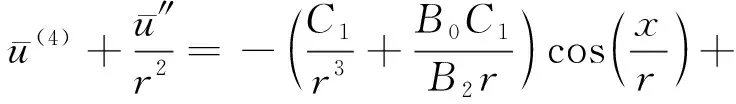
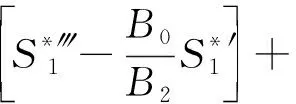
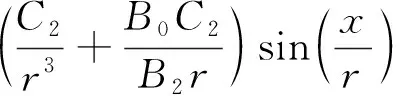
(24)

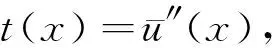
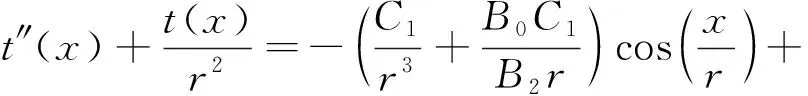
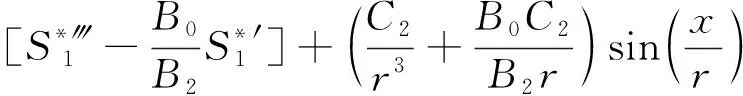
(25)

求解式(24)，可得

dd++

(26)

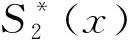
根据式(22)和式(26)，可得挠度()的分布为

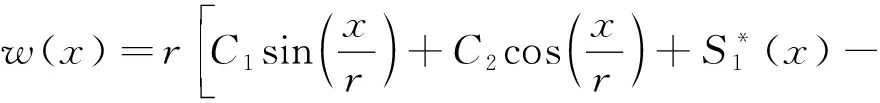
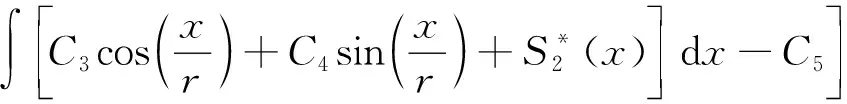
(27)

根据式(26)及式(27)可知，对于静态弯曲问题，本文理论中有6个边界条件可唯一确定上述6个待求系数，因此环结构弯曲问题从数学意义上讲是完备的。

3 环形结构的动态问题

环形谐振子结构的动态响应问题(如驻波进动效应、振动频率等问题)，一直是谐振陀螺领域的重要研究内容。因此，本节基于上述广义几何关系、本构关系及哈密顿原理，对环形结构的动态响应问题进行系统的研究。

3.1 动态问题的基本理论

对于缓慢、匀速转动过程中的环形谐振子结构，根据环结构的哈密顿原理，可得

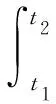
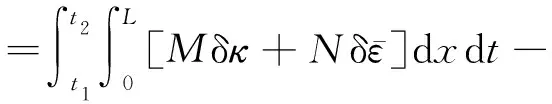
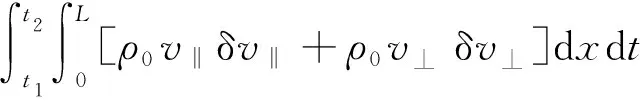
(28)

其中

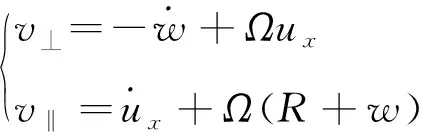
(29)

并且，和分别代表环结构中心轴处的周向速度和径向速度。

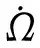
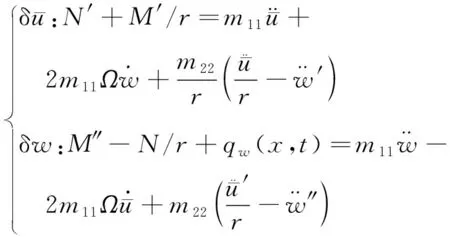
(30)

其中

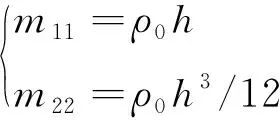
(31)

至此，建立了环形结构动态问题的控制方程，这对于求解环形谐振子的动态响应问题具有重要的指导作用。此外，环形结构的连续性(周期性)条件可一般地表述为

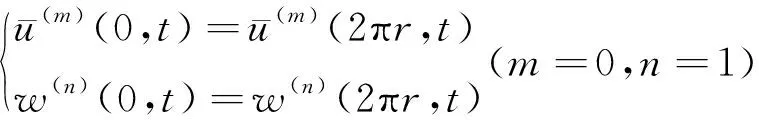
(32)

3.2 动态问题的理论解

二阶(角)频率及进动系数是谐振陀螺的重要动态响应参数，因此需要重点研究。为了获得环形结构的动态响应问题的理论解，同样引入几何中性轴(或称中心线)不可拉伸假设，考虑式(10)和式(1)之二式，从而有

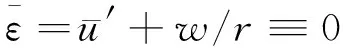
(33)

即

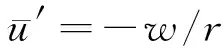
(34)

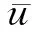
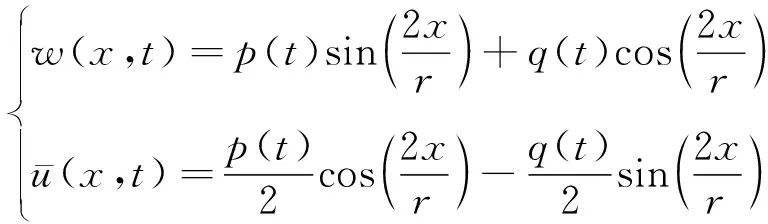
(35)

其中，()和()为分布函数，并且该分布自动满足周期性条件(见式(32))。

将式(33)和式(35)代入平衡方程式(30)，利用布勃诺夫-伽辽金法整理可得

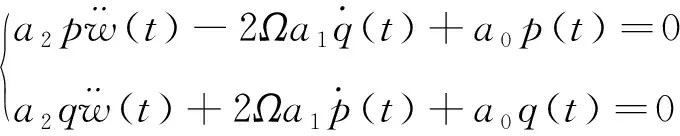
(36)

其中

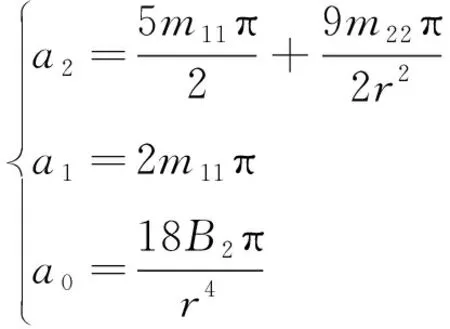
(37)

进而，进动系数和二阶角频率的理论解为

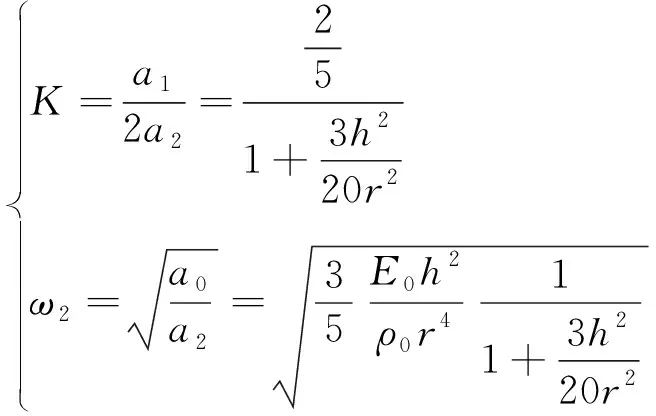
(38)

4 典型问题的求解与分析

为了减少谐振子在工作过程中的能量损耗，环形谐振子往往选用熔融石英材料，其相关力学参数如下：密度=2200kg/m，弹性模量=76.7GPa及泊松比=017。基于该材料的力学属性，本文对环形谐振子的静态弯曲问题和动态响应问题进行了求解与分析。

4.1 弯曲问题求解及分析

为了验证本文环问题的基本理论和解析求解方法的正确性，本小节对两端(即=0及=π处)受简支条件约束、均布载荷()=作用的环形结构弯曲问题进行分析。考虑上述弯曲问题的对称性，本文取二分之一圆环结构进行分析(即=π)，如图3所示。根据式(18)，上述弯曲问题的边界条件可进一步描述为

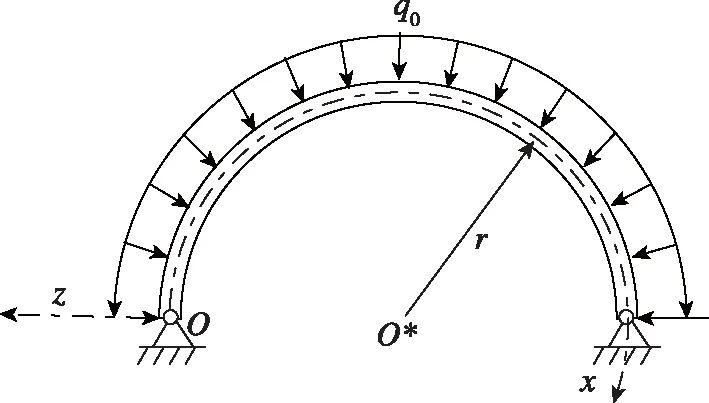
图3 环形结构受均布载荷示意图

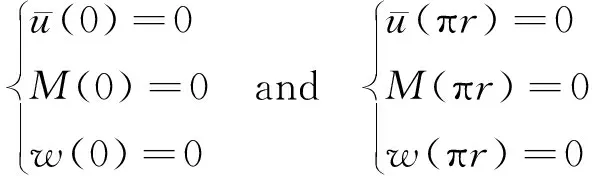
(39)

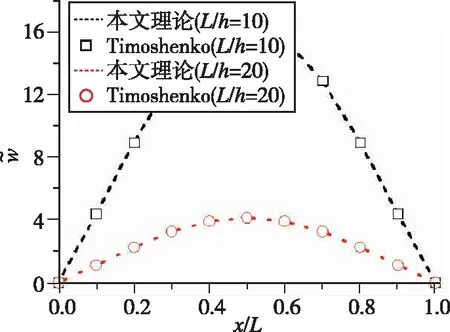
(a) 当L/h=10及L/h=20时

根据图4可知，对于上述弯曲问题，随着长高比的增加，挠度的最大值在不断减小，这是由于的增加，引起了整体结构刚度不断减小的缘故。与此同时，在长高比分别为10、20、50和100的工况下，本文理论获得解析解与Timshenko理论的解在整个区域内一致性十分好，并且具有良好的对称性，这些都充分证实了本文环形结构理论和解析求解方法的准确性。

令人遗憾的是，经典环形谐振子理论是不能求解静态弯曲问题的。根据经典环形谐振子的挠度控制方程式(1)，挠度控制方程可简化为

,+2,+,=0

(40)

显然，上述挠度控制方程无法充分反映结构特征尺寸、以及材料属性对环形结构弯曲问题的影响。事实上，造成这一问题的根本原因在于，没有厘清经典环形谐振子理论的基本条件(和假设)与理论求解的简化条件(几何中心线不可拉伸假设)之间的区别。在经典环形谐振子理论建立时，过早地将几何中心线不可拉伸假设作为约束条件引入；从数学意义上讲，该假设条件只是为获取理论解而引入的一个简化求解条件，并非是环形谐振子理论建立的基本假设(或条件)。

为克服经典理论不能求解环结构弯曲问题的不足，本文从环结构的基本假设和基本条件出发，根据虚功原理(或哈密顿原理)，建立了环结构弯曲问题的基本理论，获得的平衡方程可以精确求解环结构的弯曲问题，见式(17)或式(30)左侧项。因此，从这一方面来说，本文的环形谐振子理论具有更广泛的适用性。

4.2 动态响应求解及分析

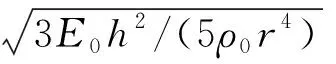
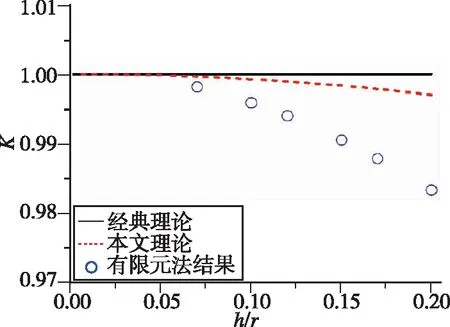
图5 二阶角频率ω2随h/r的变化规律

根据图5可知，对于二阶无量纲弯曲角频率，利用经典环形谐振子理论获得的计算结果为恒定值，而基于本文理论的计算结果不再为恒值，并且随着的增大，对应的无量纲频率在一定的小范围内不断减小，在=02时频率值降低了约0.3%，这也是基于本文理论首次获得的结果。此外，与有限元结果相比，尽管本文理论与经典理论的结果都会有一定偏差，这主要是因为本文理论与经典理论都忽略了环结构横向剪切效应所致；但是，相较于经典理论的结果，基于本文理论的解更接近于有限元分析的结果(最大相对误差小于1.4%)，这也证实了本文的计算结果具有更高的准确性。

另一方面，本文还研究了环形谐振子进动系数的分布规律。根据式(2)和式(38)，可获得进动系数随的变化规律，如图6所示。同样地，与经典环形谐振子理论的计算结果不同，本文获得的进动系数值不再恒为0.4，而是随着的增大，对应的进动系数在一定的小范围内不断减小，当=0.2时，进动系数值降低了约0.5%(降低至0.398)，这也是本文研究的另一重要理论结果。

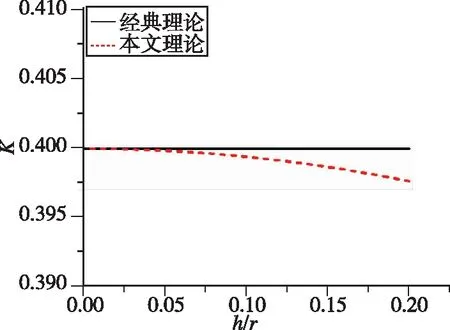
图6 进动系数K随h/r的变化规律

事实上，对于环形结构的动态响应问题(即二阶角频率和进动系数)，对比了经典理论与本文新理论计算结果之间的差异，根据式(2)和式(38)，建立两种理论解之间的联系如下

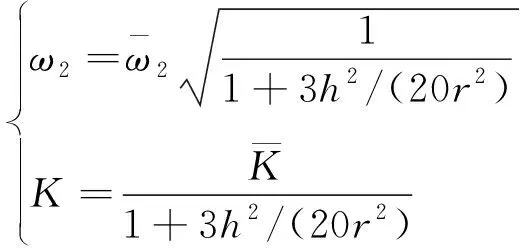
(41)

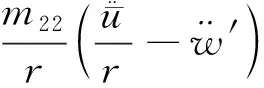
5 结论

本文从经典环形谐振子理论出发，揭示了经典理论中的不足。然后，基于环结构问题研究的基本假设和基本条件(即上、下表面剪应力自由条件)，根据线性位移模式假设、广义位移的定义、几何关系和本构关系，获得了环结构的广义本构关系，利用虚功原理和哈密顿原理，建立了新的环结构理论，包括平衡方程、边界条件、连续性条件等。同时，推导了典型环结构弯曲问题的解析求解方法及动态问题的理论解。最后，针对典型的环形结构静、动态问题，利用本文的新理论及求解方法，通过与其他理论及有限元法的结果进行对比，证明了本文的环形谐振子理论和求解方法的准确性，并剖析了经典谐振子理论中缺陷产生的原因。

本文得出的主要结论如下：

1)本文获得的环形谐振子结构的相关理论及求解方法，不仅可以求解动态响应问题，还可以求解静态弯曲问题；

2)本文获得的环形谐振子结构的二阶弯曲角频率理论解，不仅形式简单，而且更接近有限元分析结果；

3)环形谐振子的进动系数事实上不是恒定的，其值会随着结构尺寸的差异在0.4附近很小范围内变化，并且进动系数的大小与材料的力学属性(如弹性模量、密度及泊松比)无关。

此外，本文的环形谐振子理论对于高精度谐振陀螺的设计及模型误差分析(如品质因数不均匀、供电电压不稳等因素引入的误差)等研究，具有重要的工程意义和学术价值。