通信辅助卫星导航接收机最优捕获灵敏度分析

2022-06-23雷长彪

导航定位与授时 2022年3期

关键词：复杂度接收机灵敏度

王雷，雷长彪

(中国人民解放军32082部队，北京 100191)

0 引言

我国北斗三号全球卫星导航系统已于2020年完成全星座组网，提供全球定位服务。但更高性能的卫星导航定位需求仍然在不断增长，因此，准确分析当前卫星导航系统的具体能力，对于未来发展新一代的卫星导航系统具有很好的指导作用。

本文关注通信辅助下卫星导航接收机的捕获灵敏度结果。在卫星导航信号捕获阶段，通信辅助可以提供初始定位导航与授时(Positioning Navigation and Timing，PNT)信息，以降低捕获复杂度，提高捕获灵敏度。

捕获算法是一个伪码相位和载波多普勒的二维搜索过程，通信辅助通过提供包括接收机位置、卫星星历以及接收机时间等信息，有助于降低捕获中的频率不确定度以及时延不确定度，进而接收机可通过改进算法提升灵敏度。文献[3]对不同辅助信息精度下的频率搜索范围压缩程度和伪码相位压缩程度进行了分析。在此基础上对算法进行改进，以提高捕获灵敏度，文献[4]分析了辅助信息与捕获灵敏度提升量之间的关系，但是仅得出了极限的性能结果，并未考虑由此导致的计算复杂度提升。卫星导航信号捕获灵敏度是在满足系统捕获概率和虚警概率条件下所能捕获到的信号的最低载噪比，捕获灵敏度越高，意味着可接收的信号载噪比越低。为提高接收机捕获灵敏度，普遍的做法是提高相干积分时长以及非相干累加次数，从而提高相关增益。

捕获算法的两个评价标准为平均捕获时间和计算复杂度，部分文献以平均捕获时间为优化目标对算法进行改进，并分析了辅助条件下平均捕获时间的降低情况。

但目前并未有文献给出不同辅助信息条件下捕获灵敏度的具体结果，本文通过约束平均捕获时间以及计算复杂度指标，对捕获灵敏度与辅助信息精度之间的定量关系进行分析。

1 捕获算法性能评价指标

评价捕获算法的两个主要指标是平均捕获时间和捕获算法复杂度。

1.1 平均捕获时间

平均捕获时间反映的是卫星导航接收机完成信号捕获所需的平均时长，文献[8-9]给出了并行搜索条件下接收机平均捕获时间的表达式，如式(1)所示

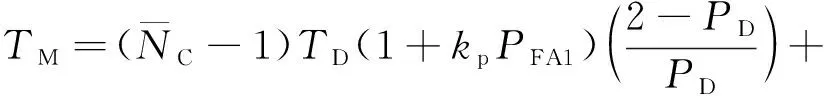
(1)

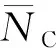
=1-(1-)=1-(1-)-1

(2)

其中，为单次并行搜索完成的单元数量。

在算法保持不变的情况下，平均捕获时间随搜索范围的减小而降低。相应地，接收机可在平均捕获时间满足指标的条件下改善捕获算法，从而实现提高捕获灵敏度的效果。

1.2 捕获算法计算复杂度

捕获算法的计算复杂度反映的是完成捕获运算所需的计算资源情况。以时域并行快速傅立叶变换(Fast Fourier Transform，FFT)捕获算法为例，其实现框图如图1所示。

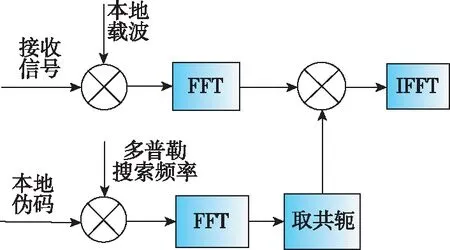
图1 时域并行FFT算法实现框图

时域并行FFT捕获算法利用FFT运算实现伪码相位的并行搜索，是一种高效的捕获算法。为保证FFT算法的效率，通常将运算点数取2的整数次幂，以表示相干积累采样点数，表示码相位搜索点数，则FFT运算点数表示为

=2(+)

(3)

其中，2()为距离最近的下一个2的整数次幂。

以表示频率搜索单元数量，则时域并行FFT捕获算法的计算复杂度如表1所示。

表1 时域并行FFT捕获算法计算复杂度

其中对于现场可编程门阵列(Field Programma-ble Gate Array,FPGA)等计算器而言，乘法器计算复杂度远高于加法器，因此在分析计算复杂度过程中主要考虑乘法器计算量。

以常用的民用导航信号为例，对计算复杂度进行分析，设定伪码速率为1.023MHz，伪码搜索范围为1ms，载波多普勒搜索范围为±5kHz，频率搜索间隔取1(2)，其中为相干积分时长，不同相干积分时长条件下的计算复杂度结果如图2所示。

图2 计算复杂度与相干积分时长的量化关系

由图2可知，捕获算法计算复杂度随信号相干积分时长的增加而逐渐增长，其中急剧增长的部分是由于FFT运算点数升级至下一个2的整数次幂；同时，受制于有限的运算器件计算资源，相干积分时长并不能无限制提高。通过上述分析可知，计算复杂度对于捕获灵敏度起着制约作用。

2 辅助接收机捕获灵敏度评估方法

根据上述分析可知，在平均捕获时间和计算复杂度的约束下，辅助信息与最优捕获算法以及可实现的捕获灵敏度之间存在特定对应关系。为明确其定量结果，本文定义辅助接收机捕获灵敏度评估方法，对于由相干积分以及非相干累加组成的捕获算法，其表达式如式(4)所示

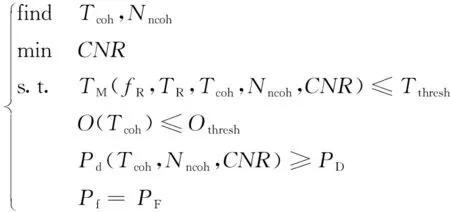
(4)

其中，为频率搜索范围；为伪码相位搜索范围；为相干积分时长；为非相干累加次数；为信号载噪比；为平均捕获时间门限；为捕获概率门限；为虚警概率指标；为计算复杂度指标门限。

由于导航信号伪码周期通常为整毫秒，因此在本文分析中，将相干积分时间取为整数毫秒。在上述条件下，本文在一定范围内对相干积分时长和非相干累加次数进行遍历，从而获得该评估方法下的捕获算法最优解。

其计算流程如下：

1)首先根据计算复杂度指标，确定相干积分时长的取值范围；

2)在一定范围内，对、进行遍历，找出使得捕获算法同时满足式(4)中所有约束的、值，对应于最低载噪比的值即为最优捕获算法的捕获参数，相应的载噪比值为最优的捕获灵敏度值。

3 捕获算法损耗分析

在上述分析中，给出了辅助接收机捕获灵敏度评估方法，为定量地分析捕获灵敏度与捕获算法的关系，对捕获算法的损耗需采用尽量精确的模型。本文在分析捕获算法损耗的过程中，对于伪码损耗考虑伪码相位与伪码多普勒损耗，对于载波损耗考虑载波多普勒和载波多普勒变化率损耗。以导航信号中主用的二进制相移键控(Binary Phase Shift Keying，BPSK)信号体制为例，相关损失表达式如下所示。

1)伪码损耗

存在伪码多普勒的情况下，相关损耗表达式如式(5)所示

(,)=

(5)

其中，为伪码频率变化率，伪码多普勒与以及伪码码率的关系为=；为伪码初相；为码片宽度；为相干积分时长内的码片数量。

2)载波损耗

当同时存在载波多普勒以及载波二阶多普勒的情况下，载噪比损耗表达式如式(6)所示

(,,)=

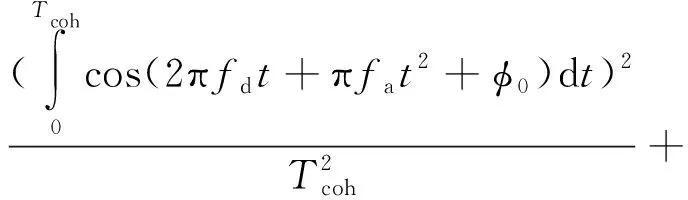
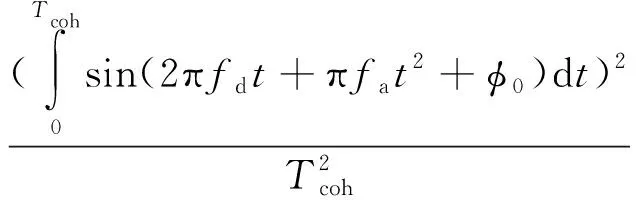
(6)

其中，为多普勒频率；为载波多普勒变化率；为初始载波相位偏差。

在采用平方律检波的条件下，基于上述损耗模型可以得出精确的检测统计量概率分布函数，据此可计算出不同、以及条件下的捕获概率与虚警概率。

4 评估结果

根据上述分析过程中建立的评估方法以及分析模型，以典型的车载设备和机载设备为例，对辅助接收机捕获灵敏度结果进行分析。

信号的动态包括卫星运动产生的动态、接收机钟差产生的动态以及载体运动产生的动态，北斗中地球轨道(Medium Earth Orbit, MEO)卫星对地面静止目标的最大相对速度为700m/s，卫星导航接收机中常用的温度补偿性晶振的频率准确度为10～10。

取不同载体类型的一组动态典型值作为辅助接收机捕获灵敏度的分析条件，具体如表2所示。

表2 载体动态典型值

结合接收机时钟性能，在不同类型载体动态典型值下，所接收卫星导航信号的动态典型值如表3所示。

表3 不同类型载体信号动态典型值

载体信号动态典型值不仅表示了信号捕获过程中载波多普勒的搜索范围，同时，多普勒变化率也是影响卫星导航信号捕获算法性能的重要因素。

4.1 灵敏度分析结果

在当前接收机设计过程中，受导航电文长度限制，相干积分时长通常不会超过20ms，为代表大多数接收机的具体情况，本文考虑算法复杂度约束下捕获算法的相干积分时长最长为20ms。

接下来，本文基于通信辅助接收机捕获灵敏度评估方法对捕获灵敏度与伪码相位搜索范围压缩和频率搜索范围压缩之间的关系进行分析。在分析过程中，以伪码相位和载波频率最大的搜索范围作为基准值，在基准值的基础上进行压缩，分析捕获灵敏度与压缩程度之间的具体关系。

经分析，不同载体类型条件下不同伪码速率信号的捕获灵敏度与伪码相位搜索范围压缩量之间的关系如图3所示。

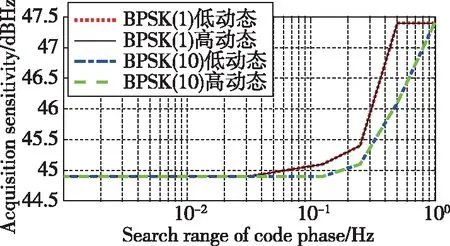
图3 捕获灵敏度与伪码相位搜索范围压缩量的量化关系

不同载体类型条件下不同伪码速率信号的捕获灵敏度与频率搜索范围压缩量的量化关系如图4所示。

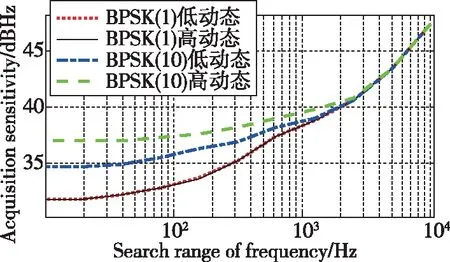
图4 捕获灵敏度与频率搜索范围压缩量的量化关系

根据上述分析，可以得出如下结论：

1)相同的压缩比例下，伪码相位压缩产生的灵敏度提升量小于频率压缩量，这与具体的捕获算法相关。本文分析过程中选用的捕获算法为并行伪码相位搜索算法，在伪码相位搜索上进行了压缩，因此进一步压缩对于算法产生的效益较小。若捕获算法采用的是串行搜索算法或者并行频率搜索算法，本结论会存在差异。

2) 对于BPSK(10)信号，伪码相位搜索范围在基准值基础上压缩至1/2的过程中，灵敏度提升量约1.3 dB，在搜索范围压缩至基准值1/4的过程中，灵敏度提升量约2.3dB；而对于BPSK(1)信号，搜索范围压缩至初始值1/4的过程中，灵敏度提升量约2.0dB。

3) 频率搜索范围在基准值基础上压缩至1/2的过程中，灵敏度提升量约4dB；在搜索范围压缩至基准值1/4的过程中，搜索灵敏度提升量约7dB。

4)随着辅助条件下频率搜索范围压缩程度的增加，每压缩1/2捕获灵敏度提升量逐步降低，达到1/32的情况下，每压缩1/2捕获灵敏度提升量开始低于1dB。

根据上述分析可知，在本文考虑的算法条件下，频率搜索范围压缩对于捕获灵敏度的提升要优于伪码相位搜索范围压缩的效果。

在上述分析过程中，捕获概率、虚警概率指标为确定值，但在接收机设计过程中，通常会根据需求对捕获概率和虚警概率进行设置。因此，接下来分析在不同的捕获概率和虚警概率指标下，辅助接收机捕获灵敏度与频率搜索范围压缩度的量化关系，具体结果如图5所示。

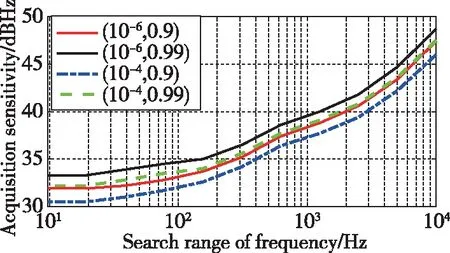
图5 不同捕获概率、虚警概率条件下捕获灵敏度与频率搜索范围压缩量的量化关系

根据上述分析可知，在不同的虚警概率和捕获概率指标下，相同的频率搜索范围对应的捕获灵敏度略有差异，但相同的频率搜索范围压缩量下捕获灵敏度提升量基本相同。

由此可知，在一定范围内捕获概率和虚警概率指标对辅助接收机捕获灵敏度提升量影响较小。因此，通过本文方法得到的辅助接收机捕获灵敏度提升量，对不同指标下的接收机设计具有一定的普适性。

4.2 捕获算法最优参数

根据上述分析，不同条件下的最优算法参数情况如表 4和表 5所示，分析可知：

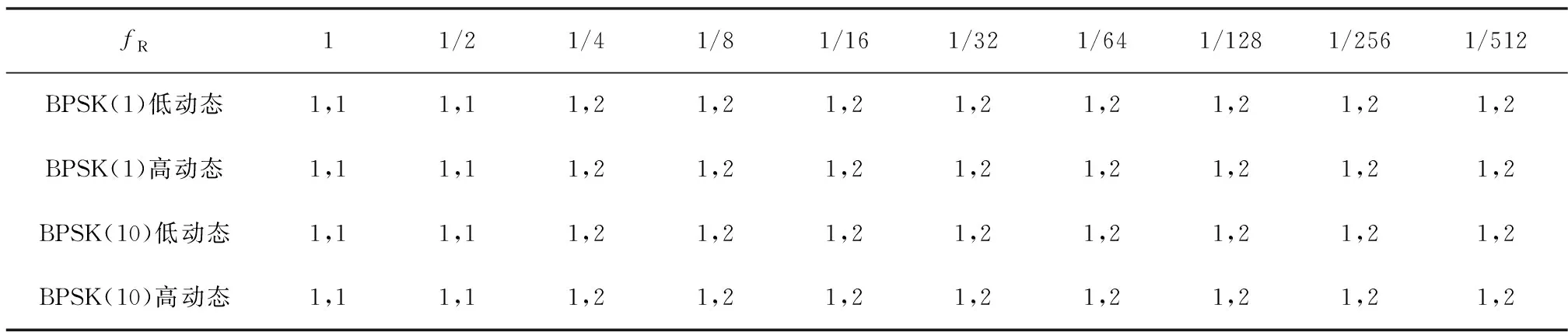
表4 辅助接收机不同伪码相位搜索范围压缩量下捕获算法最优参数(Tcoh,Nncoh)

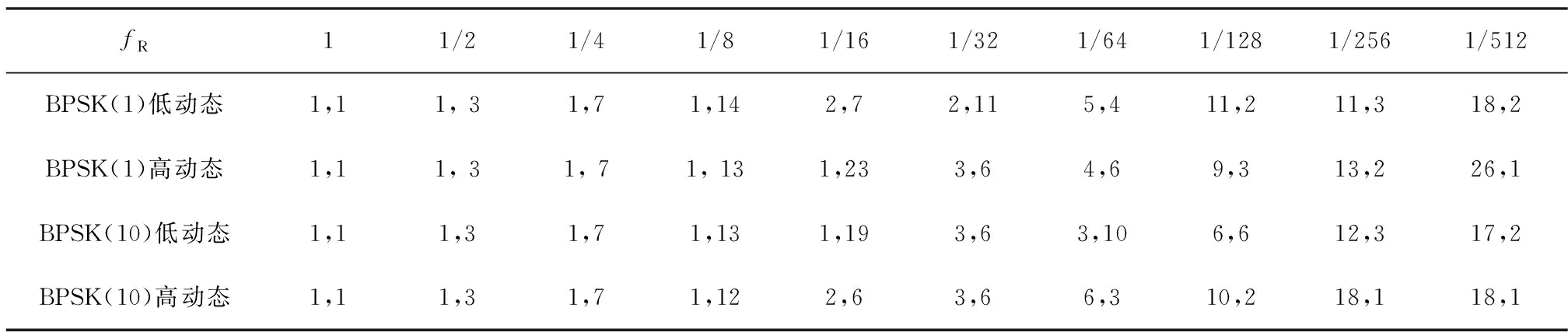
表5 辅助接收机不同频率搜索范围压缩量下捕获算法最优参数(Tcoh,Nncoh)

1)随着伪码相位压缩量和频率搜索范围压缩量的增加，最优捕获算法的总信号处理时长在不同条件下均有一定程度的增长，即算法主要通过提升总信号处理时长来提高捕获灵敏度。

2)相较于频率搜索范围压缩，伪码相位搜索范围压缩情况下的最优捕获算法总信号处理时长提升量较小，仅提高至初始值的2倍，这与在分析过程中以频率并行算法作为分析的基础有关。

3)在频率搜索范围压缩量达到初始值1/8的过程中，最优捕获算法的非相干积分时长逐渐提高，随着频率搜索范围压缩量的进一步增加，最优捕获算法的相干积分时长逐渐提高，若不考虑计算复杂度要求下的相干积分时长限制，最高达到26ms。这是由于在相干积分时长提高的同时，频率搜索数量成比例增长，容易导致平均捕获时间大幅度提升，因此将计算复杂度作为约束条件是有必要的。

4)相较于低伪码码率信号，高伪码码率信号最优捕获算法的总信号处理时长更短，这是由于高伪码码率更容易受到伪码多普勒损耗的影响，降低相关积累增益。