成都地区土层剪切波速与埋深的关系*

蔡 润，彭 涛，罗东林，周亚东，尹欣欣，郭 鹏，彭界超

(1.中冶成都勘察研究总院有限公司，四川 成都 610063；2.四川省地震局，四川 成都 610041；3.中国地震局地球物理研究所，北京 100081；4.甘肃省地震局，甘肃 兰州 730013；5.东南大学 土木工程学院，江苏 南京 211189)

0 引言

剪切波速是表征地震作用下土体动力反应的重要物理量之一。它的大小既反映了场地传播地震波的能力，又反映了土层的“软硬”程度(廖振鹏，1989；王强等，2014；郑龙等，2018；黄雅虹等，2020；宋健等，2020)。剪切波速在场地类型划分、饱和砂土或粉土的液化性判定、场地土层的动弹性模量计算、土层地震反应分析、地基处理效果评价等许多方面都有重要的作用(刘华贵，蒋文宇，2015；胡庆等，2019；段蕊等，2019；蒋其峰等，2019)。目前测试剪切波速的方法有单孔法、跨孔法或面波法等，其中单孔法应用最为广泛。现场剪切波速测试是获取可靠测试资料的最有效手段之一，但是需要投入大量的人力、物力和财力，且受技术条件、设备故障和钻孔塌孔等因素的影响，有时还不能得到理想的测试结果(贺为民等，2016；乔峰等，2019，2020；李玉影等，2019)。因此，确定某地区的剪切波速值与土层埋深的相关性，以供选址及估计抗震设计地震动参数，具有重要的工程意义。

目前，国内外大量学者针对剪切波速与埋深的关系进行了研究，如Hasancebi和Vlusay(2007)采用回归分析法给出了土耳其地区土层剪切波速预测公式；Kuo 等(2011)利用多元回归分析的方法给出了中国台湾地区剪切波速数据的拟合公式；王琦等(2018)基于天津地区地震安评的实测剪切波速资料，给出了考虑和不考虑场地类别情况下常见土类剪切波速与埋深的经验关系；蒋其峰等(2019)基于幂函数的回归模型，给出山东地区粉质黏土剪切波速与埋深之间经验关系；乔峰等(2019)以北京地区地震安全性评价报告中实测剪切波速资料为依据，给出该地区5种常见土类剪切波速与埋深之间关系的推荐模型；闫振军等(2019)搜集整理了华北地区10个城市的928个钻孔共10 703个测点的剪切波速与土层埋深之间的经验统计关系；沈方铝等(2018)研究结果表明福州市区土层剪切波速与土层埋深间的相关性较为明显(除卵石外)，一元二次多项式函数的适用性更强；宋健等(2020)依据哈尔滨市钻孔实测剪切波速数据，定性分析了剪切波速与土层埋深的关系。不同地区相同土层的剪切波速之间均存在较大差别，故土层剪切波速与埋深之间的经验公式可能存在一定的区域性。

目前对成都地区土层剪切波速与埋深的关系研究较少，且做相关的统计工作需要大量的数据样本。鉴于此，本文搜集了成都市地震的安评报告，从中提取钻孔剪切波速实测资料，统计成都地区不同土层剪切波速的区间分布频次；利用常见数学回归方程对不同土层剪切波速的数据进行拟合，得到不同岩土剪切波速随埋深变化的统计关系；根据已有数据建立成都地区关于土层剪切波速与埋深的关系的遗传神经网络模型，选用成都地区某隧道排水工程的钻孔资料对数学回归模型和遗传神经网路模型进行验证，以期为成都地区开展工程勘察、场地地震安全评价等提供参考。

1 研究方法

1.1 常见数学回归模型

土层剪切波速与埋深之间的关系可用如下模型来表示(段蕊等，2019；乔峰等，2019；宋健等，2020)：

线性函数模型：=+

(1)

幂函数模型：=

(2)

二次函数模型：=++

(3)

复杂函数模型：=(+)

(4)

式中：为土体剪切波速(单位：m/s)；为土体埋深(单位：m)；、、、、、、、、、为拟合参数。

基于上述4种模型，本文利用1stopt5.0软件对不同土层剪切波速数据进行拟合，同时使用表示拟合程度的拟合系数()、卡方值()和均方误差()对拟合结果进行评价。

拟合系数最大值为1，越接近1，说明拟合程度越好，计算公式如下：

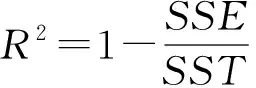
(5)

式中：为残差平方和；为总离差平方和。

卡方分布是个相互独立且服从标准正态分布的随机变量的平方和的分布，由此可知，卡方是没有负数的。卡方值越大，值(原假设为真时样本观察结果出现的概率)就越小，越能显著拒绝原假设。其计算公式如下：

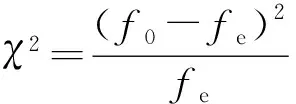
(6)

式中：表示实测次数；表示期望次数。

均方误差表示预测值和观测值之间差异的样本标准偏差，可说明样本的离散程度，其计算公式为：

(7)

1.2 遗传神经网络

BP神经网络是Rumelhart和McClelland等在1986年提出的，是一种单向传播的多层前向型人工神经网络，据统计应用BP算法的神经网络模型已达到80%～90%(蔡润等，2018；Cai，2020)。BP神经网络主要是控制误差信息的传递，若实际输出与期望输出不符，则误差信号沿原先的输入路线返回，进而影响网络内部的全部单元，获得各层单元的误差信号来作为修正网络权值的依据，故也被称为误差逆传播算法。BP神经网络具有优秀的模拟非线性系统能力和良好的预测性，特别适用于求解复杂的非线性问题，但也存在网络稳定性差、求解结果易陷入局部极值和收敛慢的缺点(蔡润等，2018)。

人工神经网络的训练性能函数采用损失函数(又称均方误差函数)，定义为：

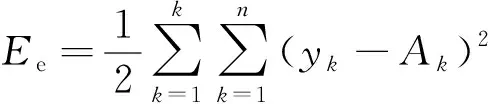
(8)

式中：为样本个数；为神经网络输出量的个数；为期望输出值；为实际输出。

遗传算法的基本思想为(蔡润，2018)：从优化问题的一个种群开始，根据适者生存的原理，逐代演化产生出越来越好的一个种群。在每一代，根据个体的适应度的优劣挑选一部分优良体复制到下一代，并对其进行选择、交叉以及变异等机制，产生出代表新的解集合的种群。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。适应度相当于“生存竞争、适者生存”的生物生存能力，在遗传算法中适应度函数的选取直接影响算法的收敛速度以及能否找到最优解，所以尽可能选择简单的适应度函数，使计算的时间复杂度最小。由于权值和阈值对结果的重要性，利用遗传算法优化后的BP神经网络的初始权值和阈值，能够更好地预测输出。使用遗传算法对BP 神经网络的优化过程如图1所示。

图1 基于遗传算法的BP神经网络算法流程Fig.1 The flow chart of BP neural network based on the genetic algorithm

2 数据整理及剪切波速分布

2.1 成都地区地质地貌概况

成都位于岷江冲洪积扇的东南缘、华夏系龙门山隆起褶带之东，属于华夏系构造中第四纪坳陷盆地，主要由第四系冲击平原、台地和部分低山丘陵组成，其地质历史悠久，地质环境条件独特，构造复杂，地层出露较全。全市地势差异显著，整体西北高、东南低，地面坡度2%～3%，西部位于四川盆地边缘地区，以深丘和山地为主；东部属于四川盆地盆底平原，是成都平原的腹心地带，土层深厚，地势平坦，海拔一般在750 m左右。

成都地区水系呈NW-SE向，除主要河流有府河、沱江河、清水河、南河等外，还有一些人工引水渠道，均属于都江堰内江水系。区域内主要分布第四系全新统()和上更新统()地层，中、下更新统()与白垩系灌口组(2)零星露头分布，地貌单元由不同类型的填土、黏土、砂土、砂砾卵石层叠置而成(汪苏华，李钟武，1990；许仲路，朱红，1991)。

2.2 数据来源及统计

本文收集了成都市地震安评资料中262个钻孔的资料，部分柱状图如图2所示。剔除数据中存在较大误差、非实测剪切波速等明显错误的数据，共有240个钻孔的6 479个剪切波速实测数据，其中岩体的剪切波速与埋深的相关性不大，因此在后续分析工作中不进行讨论。由于成都地区场地类型主要为Ⅱ类和Ⅲ类，场地类型的划分按《建筑抗震设计规范》(GB 50011—2001)的标准执行(表1)，由于Ⅲ类场地样本较少，故本文仅对成都地区Ⅱ类场地进行分析，共取得4 556个剪切波速实测数据。

表1 成都地区土的类型划分和剪切波速范围Tab.1 Classification of the soil and corresponding shear wave velocities in Chengdu region

图2 部分钻孔柱状图Fig.2 Part of the bore histograms

表2为成都地区Ⅱ类场地各类土体的剪切波速、埋深等数据统计，考虑到杂填土、冲填土、耕耘土和素填土数据量较少，故将它们统一归类为填土。本文研究的土类主要包括填土、粉土、粉质黏土、黏土、含卵石黏土、含黏土卵石、卵石等，样本埋深分布在 0～71 m。

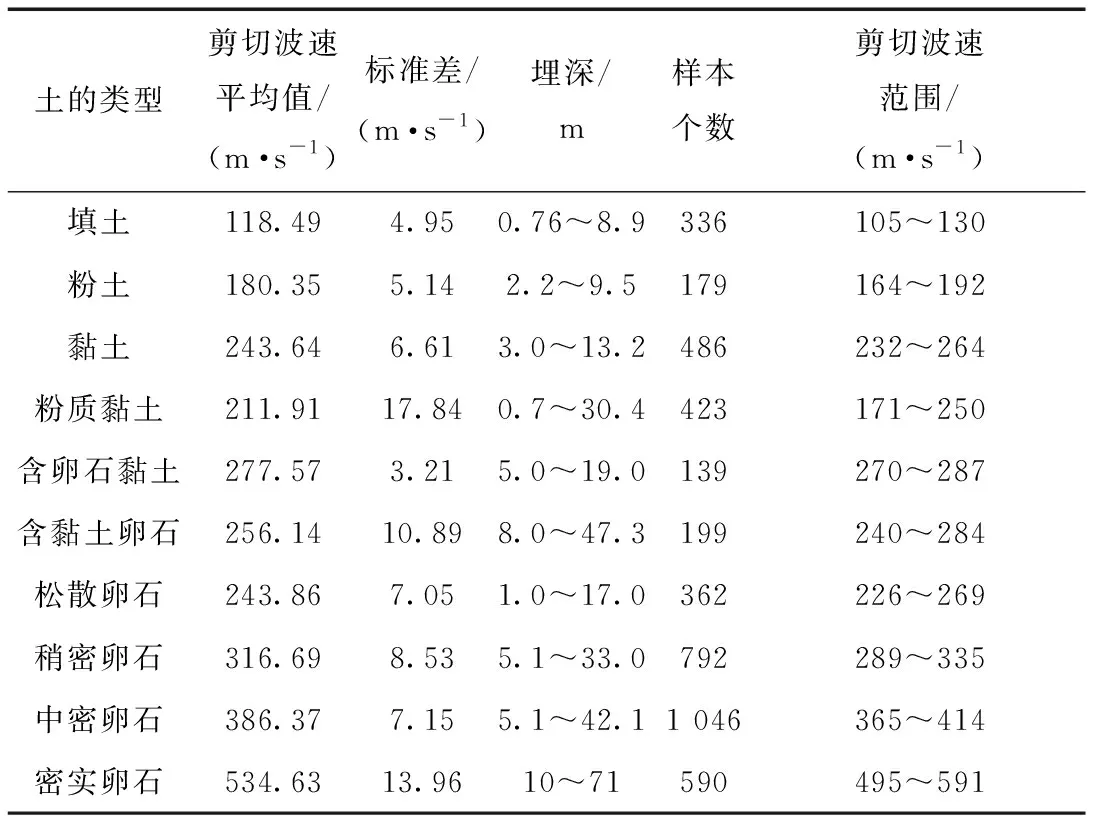
表2 成都地区Ⅱ类场地各类土体的基本信息Tab.2 Basic information of different soil on Class Ⅱ Site in Chengdu region

2.3 部分岩土的剪切波速分布特征

经统计发现，成都地区部分岩土的埋置深度分布范围较大，因此对同一类型岩土不同埋深进行分档处理，并得到不同埋深范围的统计频次，同时给出该范围内的平均剪切波速值，统计结果如图3所示。由图可见，粉质黏土的埋深范围主要集中在5～25 m，总频次为337，约占统计总频次的80%，平均剪切波速为209.5 m/s；含黏土卵石的埋深范围主要集中在8～28 m，总频次为146，约占统计总频次的73%，平均剪切波速为250.3 m/s；中密卵石的埋深范围主要集中在12～33 m，总频次为913，约占统计总频次的87%，平均剪切波速为385.9 m/s；密实卵石的埋深范围主要集中在30～60 m，总频次数为439，约占统计总频次的74%，平均剪切波速为535.4 m/s。

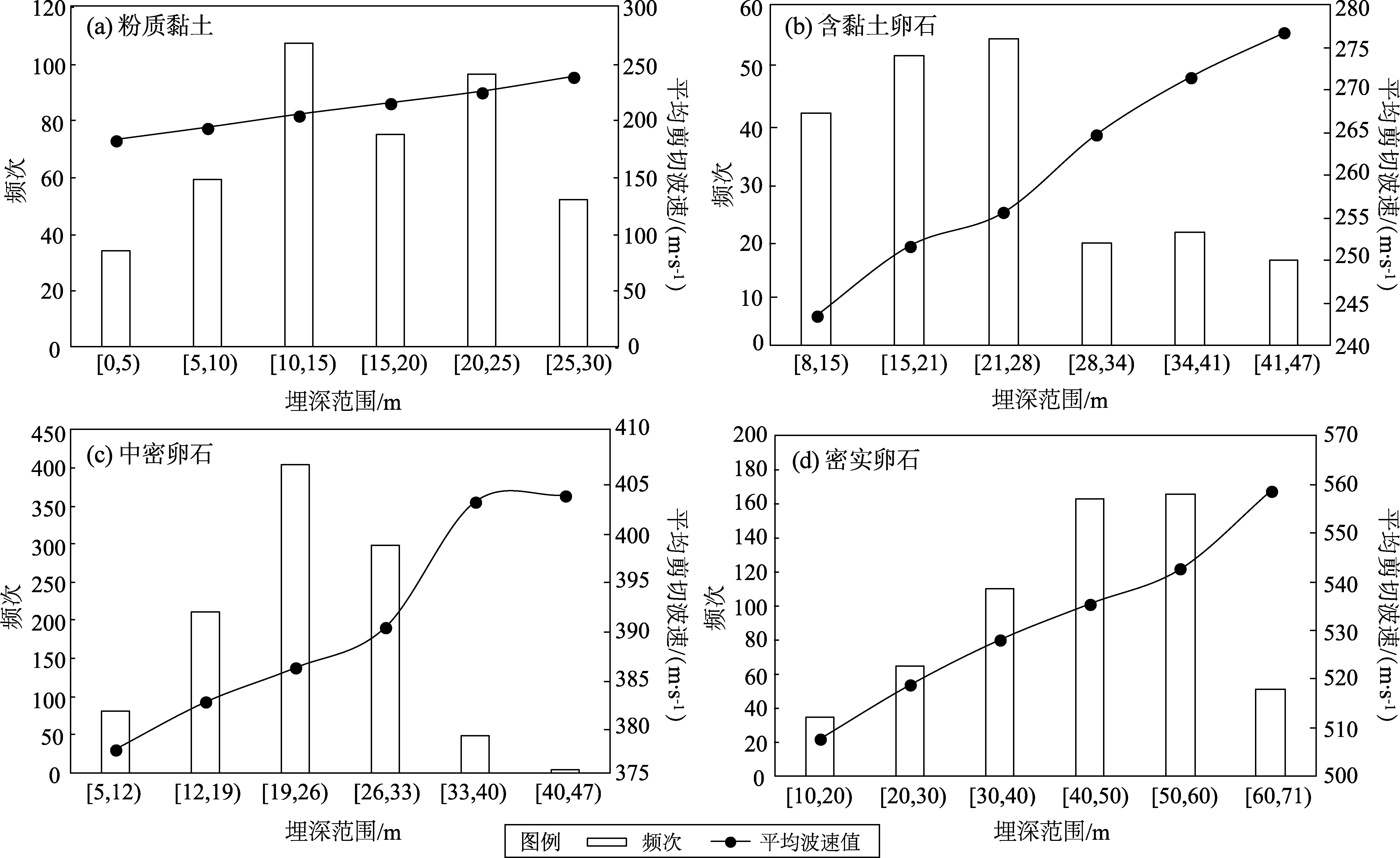
图3 成都地区剪切波速在不同埋深范围的频次分布直方图Fig.3 Histograms of the shear wave velocity at different depths in Chengdu area

本文对成都地区4种不同密实度的卵石在不同剪切波速区间的频次分布进行统计分析，同时给出正态分布曲线(图4)，主要采用期望值和方差来反映数据的集中趋势及其相对于其平均值的离散程度；采用峰度和偏态系数来描述数据分布陡缓程度及其偏斜方向和程度。

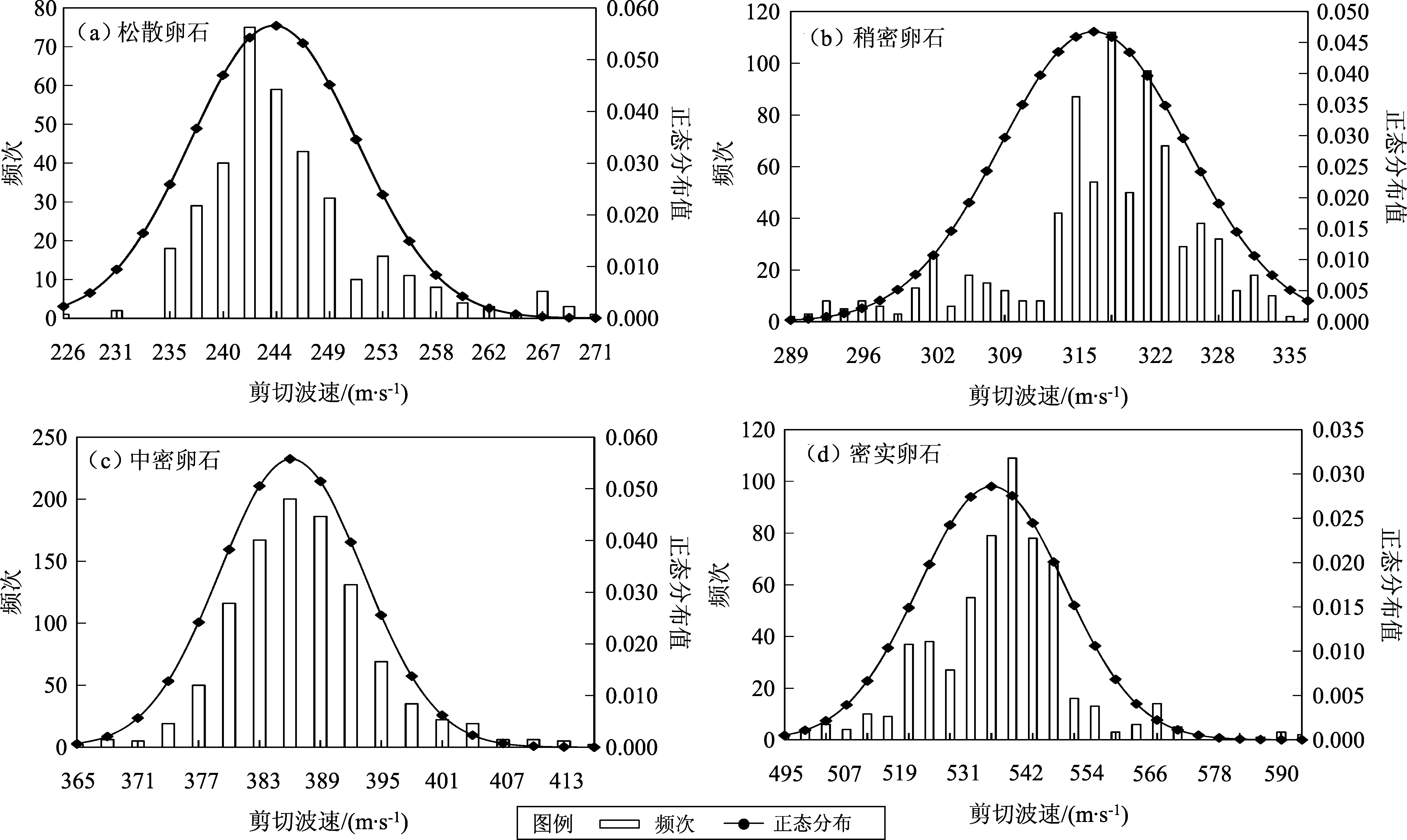
图4 4种不同密实度的卵石在不同剪切波速的频次分布直方图和正态分布Fig.4 Histograms and normal distribution of 4 types pebble soil in different shear wave velocities

松散卵石的剪切波速频次分布直方图(图4a)显示：主要呈现出单峰型的特征，峰值区间为235～249 m/s，总频次为295，占统计总频次的81%，对应于土类型中的中软土(表1)。填土的剪切波速的正态分布密度函数的数学期望和方差分别为244.98和49.72；此时的峰值为1.771 0，为正偏态，同时又小于3，说明比标准正态分布峰平缓；偏度系数为1.181 1，说明数据分布具有正偏离，即数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于左边的尾部要长。

稍密卵石的剪切波速频次分布直方图(图4b)显示：主要呈现出偏峰型特征，峰值区间为312～328 m/s，总频次为613，占统计总频次的77%，对应中硬土(表1)。填土的剪切波速的正态分布密度函数的数学期望和方差分别为317.51和72.79；此时的峰值为1.029 4，为正偏态，同时又小于3，说明比标准正态分布峰平缓；偏度系数为-0.946 3，说明数据分布具有负偏离，即数据位于均值右边的比位于左边的多，直观表现为右边的尾部相对于左边的尾部要短。

中密卵石的剪切波速频次分布直方图(图4c)显示：主要呈现出对称型特征，峰值区间为374～398 m/s，总频次为954，占统计总频次的91%，对应中硬土(表1)。填土的剪切波速的正态分布密度函数的数学期望和方差分别为387.58和51.12；峰值为1.383 3，为正偏态，同时又小于3，说明比标准正态分布峰平缓；偏度系数为0.605 2，数据分布为正偏离，直观表现为右边的尾部相对于左边的尾部要长。

密实卵石的剪切波速频次分布直方图(图4d)显示：该分布呈现出偏峰型特征，峰值区间为515～546 m/s，总频次为491，占统计总频次的83%，对应坚硬土(表1)。填土的剪切波速的正态分布密度函数的数学期望和方差分别为536.55和194.78；峰度值为2.165 1，为正偏态，同时又小于3，说明比标准正态分布峰平缓；偏度系数为0.369 4，数据分布为正偏离，直观表现为右边的尾部相对于左边的尾部要长。

3 剪切波速与埋深关系

通过统计钻孔数据提取各类土层数据，得到成都地区Ⅱ类场地土层剪切波速与埋深之间关系的散点图(图5)。由图5可知，成都地区各类常见土体的剪切波速随埋深的增大而增加，具有很强的正相关性，但不同土体剪切波速的增加率各不相同，其剪切波速的统计范围见表2。利用1stopt5.0软件对数据进行拟合，主要采用模拟退火算法计算。该算法主要是一种模拟金属退火过程的随机搜索方法，其过程描述为在给定初温下，通过一定的进度表缓慢降低温度参数值，使得SA在搜索空间里能够找到最优解(柳玲等，2009；王宝楠等，2021)。该算法的鲁棒性强，适用于并行处理，主要用于求解复杂的非线性优化问题，本文将降温速度设置为0.99。

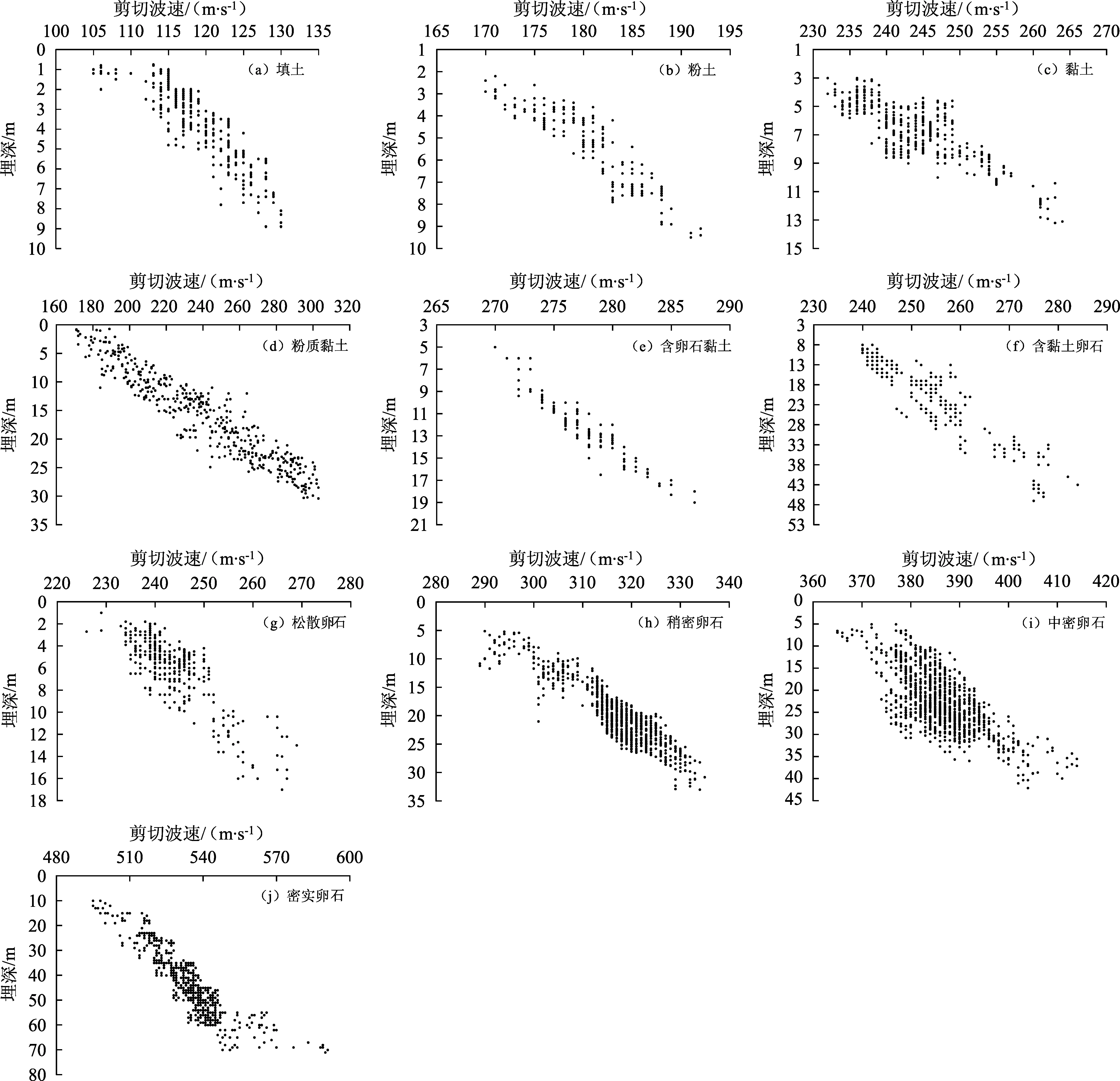
图5 成都地区各类土体剪切波速与埋深关系的散点图Fig.5 Shear wave velocity of soil versus the depth in Chengdu region

本文利用4种常见数学回归模型分别对不同类型土体数据进行回归拟合，得到成都地区各类土体数学回归模型的拟合参数和拟合优度(表3)。

表3 成都地区内Ⅱ类场地常规土类回归模型的拟合参数和拟合优度Tab.3 Fitting parameters and goodness of conventional soil regression model for type II site in Chengdu region

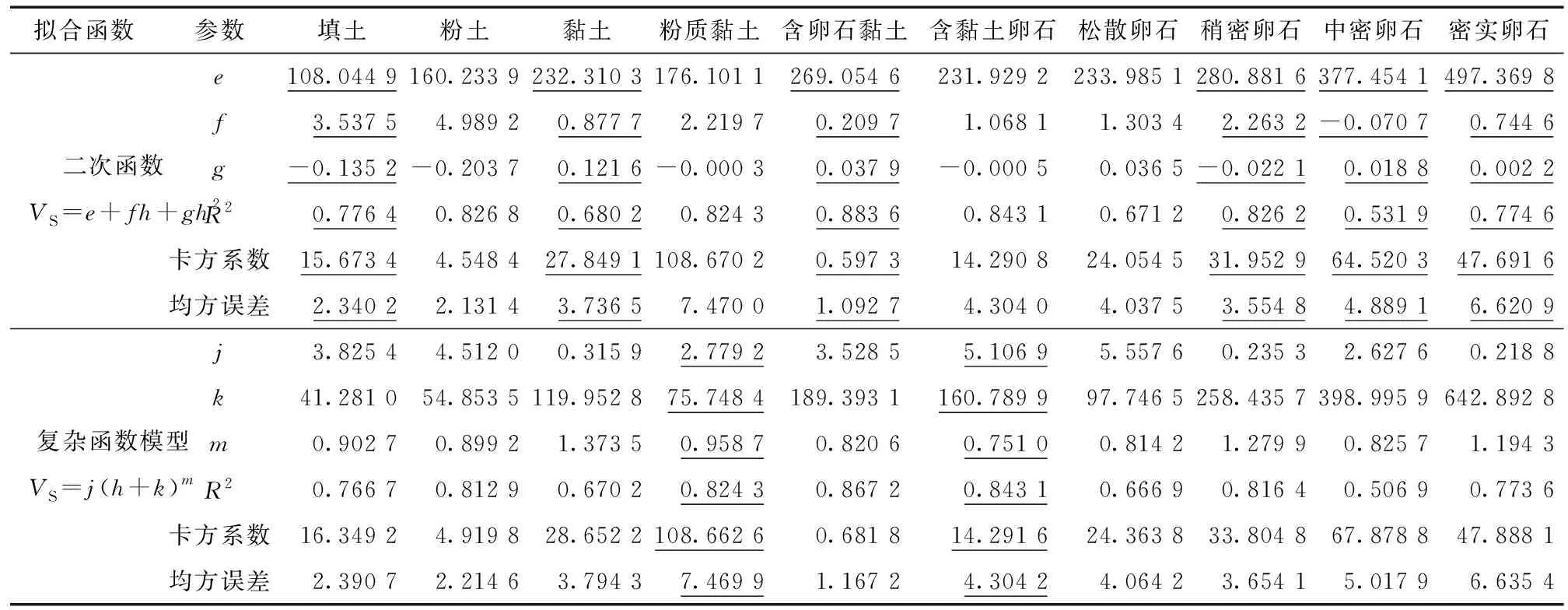
续表3

从表3可见，成都地区各种常见土类的剪切波速与埋深间都存在明显的关联性，不同数学回归模型针对不同类型土样的回归拟合效果均不一致，故针对不同类型的土样，可选择不同的数学回归模型。结合3个评价指标进行分析，推荐不同类型土样的拟合模型分别为：填土、黏土、含卵石黏土、稍密卵石、中密卵石、密实卵石的拟合模型为二次函数，即=++；粉土拟合模型为幂函数，即=；粉质黏土、含黏土卵石拟合模型为复杂函数模型，即=(+)；松散卵石拟合模型为线性函数，即=+，每种模型的推荐使用参数见表3中加下划线数字。

4 模型验证

为验证本文推荐模型的可靠性，笔者选取成都地区某隧道排水工程的钻孔资料，将本文模型预测的剪切波速与本地实测钻孔剪切波速、结合《构筑物抗震设计规范》(GB 50191—2012)和刘红帅等(2010)得出的模型(下文将这两种模型统称为“其它模型”)进行对比分析，其中相对误差表示预测值与实测值之差占实测值的比值。本文将采用数学回归模型和遗传神经网络模型分别对钻孔资料的数据进行拟合。

4.1 数学回归模型

笔者选取10个钻孔资料中的部分剪切波速数据，结合本文推荐的每一种土样的数学回归模型，计算剪切波速预测值。《构筑物抗震设计规范》(GB 50191—2012)中给出了常规土样与埋深间关系的模型(下文简称“《规范》模型”)，但只给出了黏土、卵石等相关拟合函数，并未涉及填土、粉土。因此笔者结合刘红帅等(2010)给出的相关拟合公式进行对比分析，得到各个模型对应的相对误差。由于填土、含卵石黏土以及含黏土卵石并未查阅到相关的研究成果，因此不再对比其实验结果。

由表4可知，本文数学回归模型得出的结果整体上优于其它模型，所得到的剪切波速预测结果更接近实测数据，虽然个别数据点表现较差，但相对预测误差均控制在12%以内。其它模型主要针对全国范围内各土类剪切波速与埋深相关性进行的研究，而本文模型与其他模型得出结果的差异性也正说明了土层剪切波速与埋深间关系可能受到区域性的影响。

表4 基于本文数学回归模型、遗传神经网络模型及其它模型按土体埋深所得剪切波速预测值(Ⅱ类场地)Tab.4 Predicted shear wave velocities according to the soil depth based on the model of genetic neural network， the mathematical regression model by the author，and the model by Liu

4.2 遗传神经网络模型

笔者利用样本中的4 556个剪切波速实测数据进行遗传神经网络模型训练。遗传算法的遗传代数同误差的变化如图6a所示。由图可知，BP神经网络在开始阶段误差的变化较为明显，而随着不断的优化，误差变化的幅值越来越小，说明此时的模型结构趋于稳定。经过遗传算法优化后的BP神经网络训练结果如图6b所示。从图中可以看到，经过遗传算法优化处理后的样本数据在训练过程中用较少的训练次数就可达到期望的均方误差，训练速度很快，这是由于通过遗传算法寻优后，确定出了网络模型的权值和阈值，而此时BP神经网络的权值就无需再随机赋值。为了进一步检验训练后网络的性能，对训练结果做进一步仿真分析，即对遗传神经网络仿真的输出结果和实测值作线性回归分析(图6c)，得到两者的相关系数达到0.910 96。

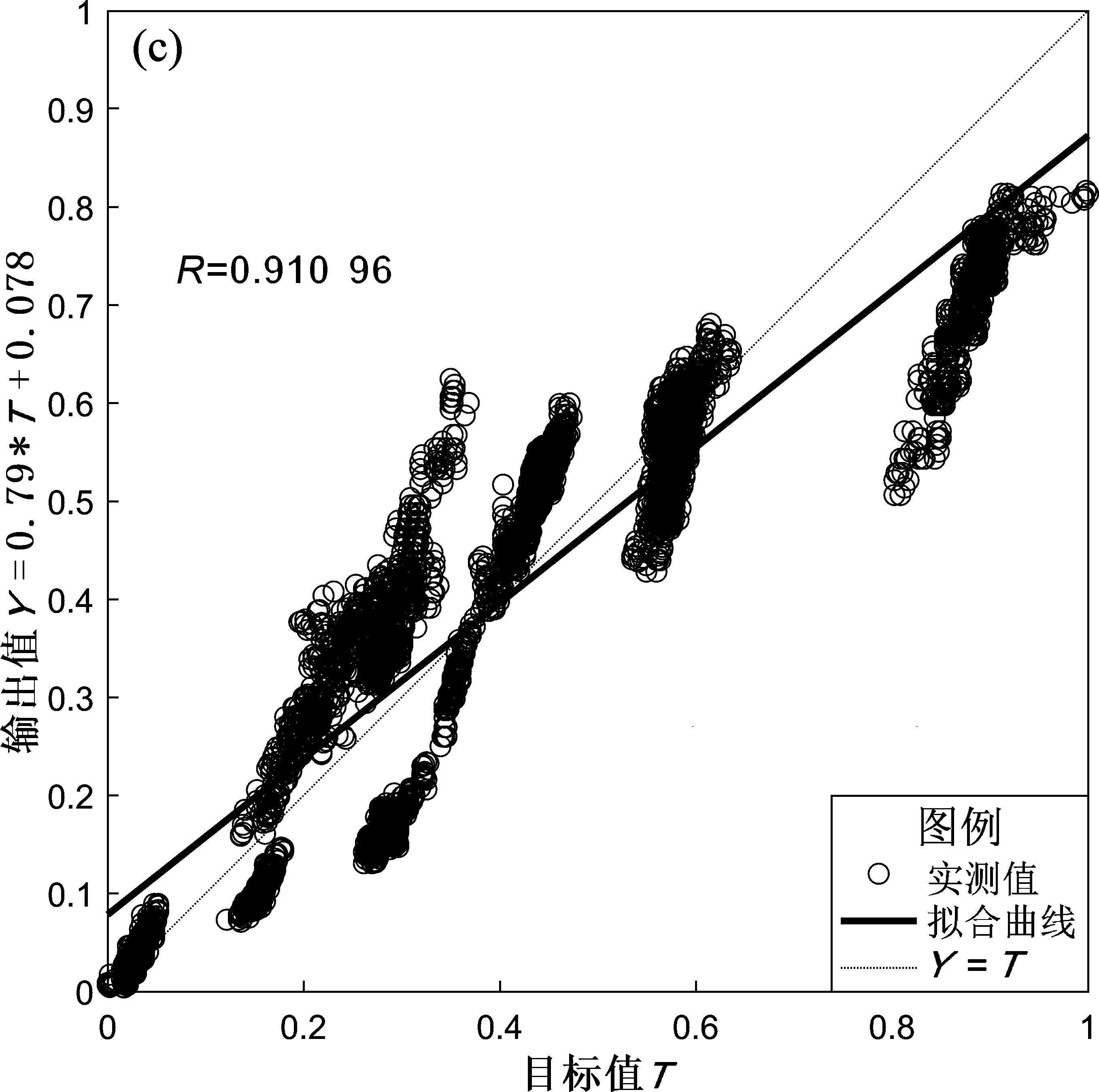
图6 遗传代数同误差值(a)、实验误差平方和随训练次数(b)变化曲线及遗传神经网络模型输出回归分析(c)Fig.6 Curve of variation of genetic algebra and error value(a)，sum of squares of experimental errors vs training times(b)，and the recursive analysis of GA-BP network output(c)

对学习样本进行网络训练后，需用实测样本对其进行测试，即利用仿真函数来获得网络的输出，通过检测输出值和实测值之间的误差是否满足要求来验证模型的可靠性，利用sim函数进行仿真处理后可得到预测值。同样选取成都地区某隧道排水工程的钻孔资料进行测试，遗传神经网络模型的输出结果见表4。从表4可以看到，遗传神经网络模型与其它模型相比，预测值与实测值更加接近，误差更小，精度更高，更加适用于成都地区的各土类剪切波速与埋深相关性分析应用。

为了更直观地观察预测效果，将本文的数学回归模型和遗传神经网络模型，与其他模型得到的剪切波速预测值及实测值进行比较，如图7所示。由图可见，本文数学回归模型和遗传神经网络模型输出的结果较为稳定，误差更小，与其它模型的预测结果相比有明显改善。

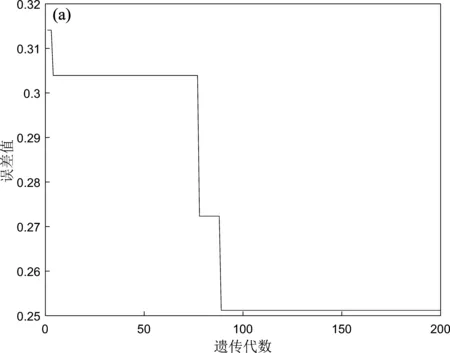
图7 不同方法的输出结果对比Fig.7 Shear wave velocities obtained by different models

5 结论

本文基于成都地区地震安评报告中的实测钻孔数据，分别利用4种回归函数模型和遗传神经网络模型，定性探讨了成都地区常见土类剪切波速与埋深的相关性，同时给出各类土剪切波速与埋深的经验公式。并以成都地区某隧道排水工程的钻孔剪切波速实测值为例，将本文推荐的两种模型与其它模型的计算结果及实测值进行对比，得出的主要结论如下：

(1)成都地区覆盖土层的剪切波速与埋深间存在一定相关性，且随埋深的不断增大，离散程度也增大。

(2)采用本文推荐的数学回归模型，剪切波速预测值与实测值相对误差在12%以内；遗传神经网络模型输出的剪切波速值与实测值相对误差在15%以内，说明这两种方法均具有较合理的可靠性。

(3)通过对同一数学回归方程应用在不同地区的输出结果进行对比可知，区域性可能对剪切波速与埋深间的经验公式存在较大影响，主要表现在预测精度方面。

本文仅考虑了不同土类的剪切波速同埋深的相关性，并未考虑其它因素的影响，如土体的状态、地质成因、土的含水量和周围环境等因素，而且也未分析土层剪切波速与土体其余物理力学参数之间的相关性，在未来还有必要做进一步的研究。