区域公路网震后连通可靠性分析及系统功能恢复*
2022-06-23蒋礼果黄淑萍
蒋礼果,黄淑萍
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
0 引言
公路是生命线工程的组成部分,也是抗震救灾的重要保障。一旦强震来袭,公路网的局部结构破坏可能会导致公路中断,甚至是路网系统的瘫痪,阻碍人员疏散和物资运输(李廷辉等,2021)。所以,对局部结构破坏引起的区域公路网连通功能损失的分析在震后抢险救灾中至关重要。连通可靠性是评价系统连通功能的重要指标,表示两节点间连通的概率,其连通状态为连通或中断(Mine,Kawai,1982)。一些学者将连通可靠性用于城市路网的抗震分析,重点研究倒塌建筑产生的瓦砾阻塞量以及受损的桥梁对路网功能的影响。李健等(2017)基于综合瓦砾阻塞量计算路段的通行概率,并以此评价上海豫园区域路网中路段的连通可靠性。何祥等(2016)从瓦砾阻塞量和桥梁震害方面计算道路连通概率,并以连通概率确定城市道路的剩余通行能力,从而构建震害下交通系统的级联失效模型。Tang和Huang(2019)根据瓦砾阻塞量和桥梁震害经验预测路段的连通概率,对城市路网进行抗震脆弱性评价。也有学者将连通可靠性用于乡村路网的抗震分析,关注点主要为地震及其引起的次生灾害对路网功能的影响(Aydin,2018)。2008年汶川8.0地震震后调查发现,区域公路网覆盖范围广,路基路面破坏、桥梁毁坏、隧道坍塌、边坡崩滑是其主要震害形式,也是影响路网连通可靠性的主要因素(李英民等,2009;王明文等,2012),这不同于城市沿街建筑物倒塌导致的道路阻塞。因此,有必要根据路段、桥梁、隧道和边坡的破坏对区域公路网震后连通可靠性进行分析。
交通网络系统的防震减灾工作包括3个阶段:震前防御阶段、震后应急阶段和震后中长期修复阶段(Bensi,2010)。其中地震应急阶段的策略是最重要和最直接地降低震害损失和恢复系统功能的方式,遵循“识别-评估-修复”的顺序,即检测路网的实际震害状况,分析路网的功能损失情况,制定相应的修复策略(邓亚娟等,2009)。在有限资源条件下,短期内不可能修复所有的受损设施,因此修复策略的重点在于确定单元修复次序(杨静等,2019)。考虑到地震发生的不确定性和震害形式的多样性,本文采用经验预测方法计算公路单元的通行概率,通过贝叶斯网络分析,建立适合区域公路网震后连通可靠性的分析模型,并结合敏感度分析和贝叶斯更新,识别区域公路网的关键单元修复优先级,为震后系统功能恢复提供依据。
1 公路单元的抗震可靠性
目前,公路单元的震害预测方法包括结构可靠性分析和震害经验统计。结构可靠性分析侧重于单个结构物的震害预测,建模复杂(孙海,高惠瑛,2017)。震害经验统计法是根据历史资料和大量震害样本进行的统计回归分析,预测结果随样本量的增加而更加可靠,适用于具有相同结构特征的单元群体的震害预测(杨翰雯,欧进萍,2019)。本文引入通行概率量化公路单元的抗震可靠性,通行概率是指公路设施不被地震破坏而能使车辆保持通行的可能性。考虑到区域公路网单元数量多且结构复杂,采用震害经验预测法计算路段单元、桥梁单元、隧道单元和边坡单元的通行概率。
1.1 路段单元
本文采用李永义(2014)提出的震害经验预测方法计算路段单元的通行概率,该方法给出了地震烈度、路基土和场地类别等7个震害影响因素的量化值(表1)以及路段单元的震害指数的经验算式:

表1 路段单元的震害因素量化值Tab.1 Quantitative values of seismic damage factors for road units
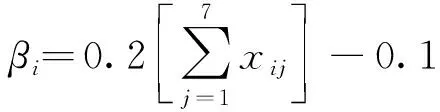
(1)
式中:是第个路段单元的第个震害因素的量化值;是路段单元的震害指数。
道路的破坏程度一般为基本完好、轻微破坏、中等破坏、严重破坏和完全破坏5个等级,对应的震后道路通行状态为允许通行、限制通行和禁止通行。
在允许通行和限制通行状态下,道路的破坏程度越高、其通行概率越低;在禁止通行状态下,道路的通行概率为0。震后道路通行概率与道路震害指数之间的关系为:
=1-
(2)
结合表1、式(1)和式(2),可以计算出路段单元的震害指数。然后根据表2判断所属区间,从而确定路段单元的震害程度和对应的通行概率。

表2 路段单元的通行概率Tab.2 Passing probability of road units
1.2 桥梁单元
本文使用朱美珍(1994)提出的桥梁震害经验预测方法计算桥梁单元的通行概率,该方法总结了9类震害因素的系数值(表3),并给出公路桥梁震害预测的经验算式:
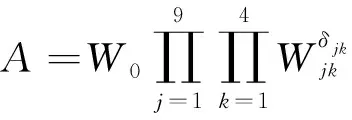
(3)
式中:是桥梁单元的震害指数;是计算系数,取值为085;是第项震害因素中第类的加权系数值(表3);是观测系数;当第项震害因子中有第类因素时=1,否则=0。
结合表3和式(3),可以计算出桥梁的震害指数;然后,根据表4(李英民等,2009)判断所属区间,从而确定桥梁单元的震害程度以及对应的通行概率。

表3 桥梁单元的震害因素系数值Tab.3 Coefficients of seismic damage factors for bridge units

表4 桥梁单元的通行概率Tab.4 Passing probability of bridge units
1.3 隧道单元
本文采用Fang等(2008)提出的震害经验预测方法计算隧道单元通行概率,该方法给出7种隧道震害影响因素的量化值(表5),隧道的震害经验预测算式为:

(4)
式中:是隧道单元的震害指数,当≤0时,取=0,当>1时,取=1;是第项震害因子中第类的计算系数值(表5);是观测系数,当第项震害因子中有第类因素时,=1,否则=0。
根据式(4)和表5,可以计算出隧道单元的震害指数;然后,通过表6(李英民等,2009)判断所属区间,从而确定隧道单元的震害程度及其对应的通行概率。

表5 隧道单元的震害因素系数值Tab.5 Coefficients of seismic damage factors for tunnel units

表6 隧道单元的通行概率Tab.6 Passing probability of tunnel units
1.4 边坡单元
本文使用王余庆等(2001)提出的边坡震害经验预测的方法计算边坡单元通行概率,该方法综合考虑地质、坡角、坡高、降水强度和地震烈度5个主要震害因素,对各因子分级赋值(表7),边坡震害的经验算式为:

表7 边坡单元的震害因素赋值Tab.7 Valuation of seismic damage factors for slope units
=(××)(+)
(5)
式中:是边坡的震害指数;是地质条件,=×;是坡角;是坡高;是地震烈度;是降雨强度。

表8 边坡单元的通行概率Tab.8 Passing probability of slope units
2 区域公路网连通可靠性分析模型
2.1 贝叶斯网络构建
区域公路网是一个复杂的物理网络系统,再加上地震发生的不确定性,因此区域公路网震后连通可靠性的分析较为复杂。贝叶斯网络作为一种概率图模型,既可以根据条件概率关系整合不确定性变量之间的联系,也能基于实时的观测信息和专家意见动态评估系统功能,是处理不确定性问题的有效工具(Kabir,Papadopoulos,2019)。故本文将其应用于区域公路网震后连通可靠性分析模型的构建,具体的建模过程有3个步骤:
(1)事件树分析
分析区域公路网震后连通可靠性之前,需要明确公路单元、公路段、路径和OD(Origin-Destination)之间的连通逻辑。事件树是一种可以将系统事故与导致事故原因之间的逻辑关系用树形图表示的分析方法,区域公路网震后连通的事件树如图1所示。在该事件树中,当一条公路段上所有单元连通时,那么该条公路段是连通的;当一条路径上的所有公路段都连通时,该条路径才连通;而当一对OD的所有路径中有一条是连通的,那么此OD是连通的。

图1 公路网连通的事件树Fig.1 Event tree of highway network connectivity
(2)成功树构建
成功树可以依据成功事件的发生概率以及事件之间的逻辑关系计算顶事件成功的概率。先通过网络分析确定公路单元、公路段、路径和OD对之间的构成关系,然后根据事件树分析得到它们之间连通逻辑,构建区域公路网对应的成功树,如图2所示。OD连通是顶事件,公路段连通和路径连通是叶节点事件,公路单元连通是底事件。每个事件都有两个状态:连通状态用1表示,中断状态用0表示。公路单元、公路段、路径、OD之间的连通关系用与或门(AND-OR)表示,其中与门(AND Gate)是指与某个父节点事件相连的所有子节点事件都发生时,该父节点事件才发生。或门(OR Gate)是指与某个父节点事件相连的子节点事件中,只要有一个发生,那么父节点事件就会发生。

图2 公路网连通的成功树Fig.2 Success tree for highway network connectivity
(3)成功树转化为贝叶斯网络
贝叶斯网络所需参数为根节点的概率分布和其它节点的条件概率分布。成功树转化为贝叶斯网络有以下步骤:首先将成功树中的事件与贝叶斯网络中的节点一一对应,重复的事件合并为贝叶斯网络中的一个节点。然后,将输入事件对应的节点通过有向弧连接到逻辑门对应输出事件的节点,并把成功树中的与门和或门转化为贝叶斯网络中节点的条件概率表,如图3所示,若和为1,表示事件发生;和为0,则表示事件不发生。

图3 与门(a)和或门(b)对应的贝叶斯网络Fig.3 Bayesian network corresponding to AND gate(a) and OR gate(b)
通过上述步骤可以得到区域公路网对应的贝叶斯网络,然后将公路单元的抗震可靠性作为贝叶斯网络的先验概率,计算分析区域公路网震后的连通可靠性。
2.2 基于贝叶斯更新的系统功能恢复
本文系统功能的修复策略表现为关键单元及其修复优先级的识别。关键单元是指那些抗震可靠性发生轻微变化时,关联的OD对连通可靠性发生最大变化的单元。Kjærulff和Gaag(2000)提出的贝叶斯网络下的敏感度分析被用于识别关键单元,其中贝叶斯网络下OD节点的连通可靠性表示为:
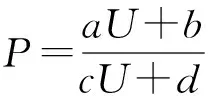
(6)
式中:是贝叶斯网络中OD节点的连通可靠性;(0<<1)是单元节点的抗震可靠性;,,,是计算系数。根据关键单元的定义,可以得到敏感度系数,即OD节点的连通可靠性对单元节点抗震可靠性的导数:

(7)
当=0/1时,公路单元的状态为中断或连通,单元中断或连通是一个必然事件,此时单元的敏感系数为0。敏感度分析中,具有最大敏感度系数值的单元可以确定为该OD的关键单元,从而推断公路网在当前状态下的关键单元。
为快速修复震后公路网系统的连通可靠性,使用基于贝叶斯更新的启发式方法识别关键单元的修复优先级:①将公路单元抗震可靠性作为贝叶斯网络的先验概率,计算贝叶斯网络中各节点第阶段(初始阶段为第1阶段)的连通可靠性;②采用敏感度分析识别第阶段的关键单元;③修复步骤②中的关键单元至期望抗震可靠性(Expected Seismic Reliability,0~1);④将被修复单元的抗震可靠性作为新的概率输入,更新区域公路网震后连通可靠性分析模型,得到第+1阶段的连通可靠性和关键单元;⑤重复步骤②~④,直到某一阶段识别出的关键单元的抗震可靠性满足期望抗震可靠性。
3 实例应用
本文研究对象是2008年汶川8.0地震中由G213和S9构成的区域公路网,该公路网位于都江堰市和银杏乡之间,途经震中映秀镇,如图4所示。

图4 由G213和S9构成的区域公路网Fig.4 Regional highway network consisting of G213 and S9
节点①、②和③是交叉口;节点①、②和④分别对应都江堰市、映秀镇和银杏乡的应急救援中心;公路段S1(①—②)、公路段S4(②—③)和公路段S5(③—④)位于G213,公路段S2(①—②)和公路段S3(②—③)位于S9。双线设计被纳入考虑,使用左线LL和右线RL区分相应的公路段。地震发生后,应急救援中心通常是抗震救灾运输任务的起点或终点,所以本文将节点①、②和④设置为应急救援任务的起点或终点,对应O1D2,O2D1,O1D4,O4D1,O2D4和O4D2。公路单元震害数据来源于《汶川地震公路震害调查》(陈乐生,2012)。根据公路单元通行概率的计算方法,可以得到公路单元的抗震可靠性,见表9。
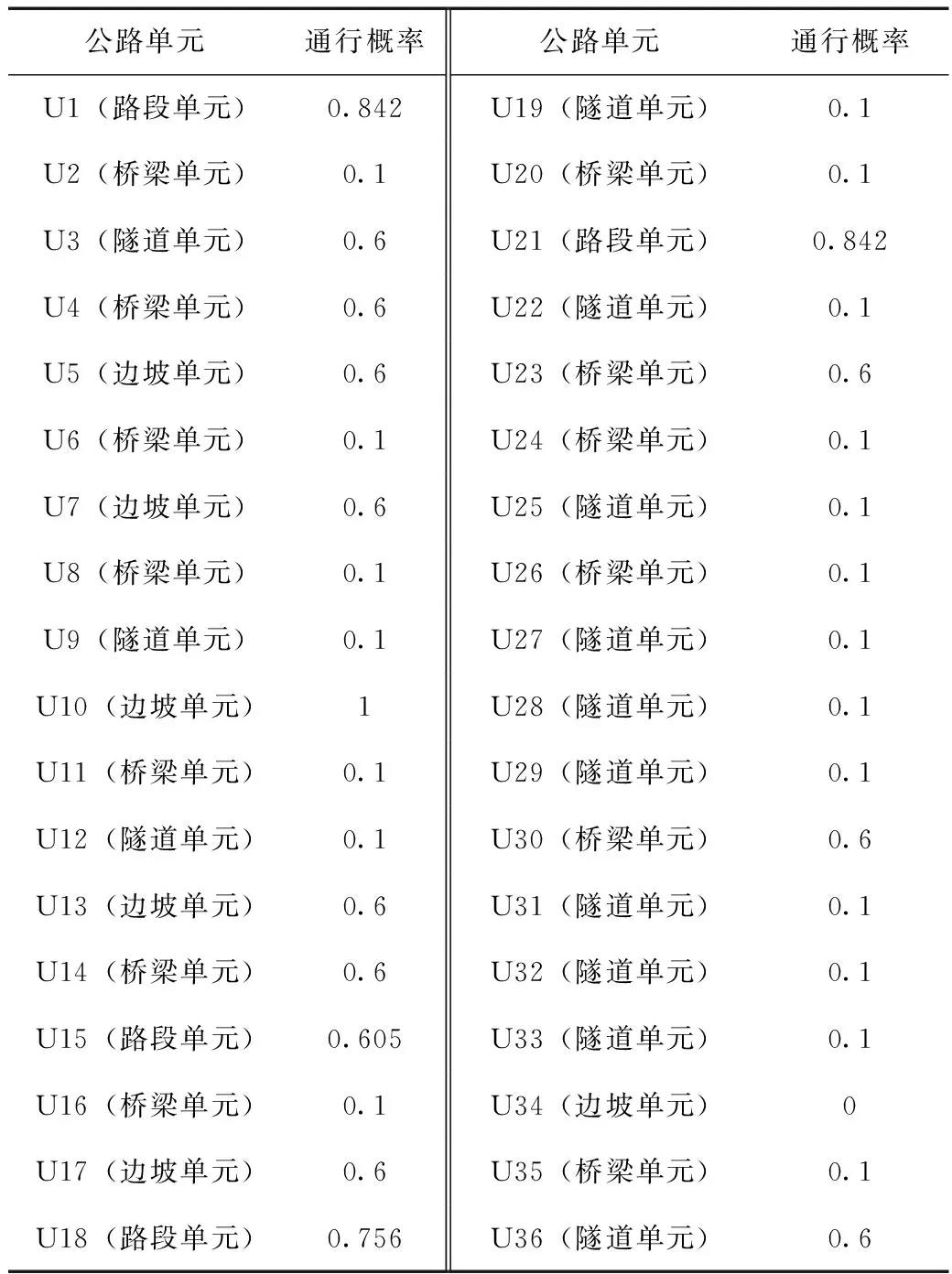
表9 汶川地震中公路单元的通行概率Tab.9 Passing probability of highway units in the Wenchuan Earthquake region
根据贝叶斯网络的构建方法,可以得到区域公路网对应的贝叶斯网络。当指向一个节点的父节点数量超过3时,中间节点I1~I14加入到该网络模型,用以降低条件概率表的规模,实现贝叶斯网络的优化计算(Kabir,Papadopoulos,2019),最终的贝叶斯网络如图5所示。在贝叶斯网络中,一个有个二态父节点的子节点的条件概率表的规模为2+1,如果一个数字存储需要8字节,共需要8×2+1字节的计算机存储空间。条件概率表的规模会随着父节点数量的增加呈指数级增长,这严重制约贝叶斯网络的计算效率。加入中间节点前后,本文贝叶斯网络的条件概率表所需存储空间分别为16 390.0625 KB和3.75 KB,所以中间节点能够极大降低计算机存储空间并在一定程度上提高计算效率。
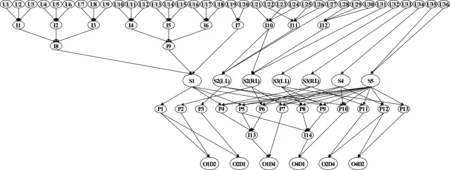
图5 公路网的贝叶斯网络模型Fig.5 Bayesian network model of the highway network
将公路单元的抗震可靠性作为贝叶斯网络的先验概率输入,构建区域公路网连通可靠性分析模型。假设关键单元完全修复,即期望抗震可靠性=1,被修复单元的抗震可靠性恢复至1;然后采用启发式方法,得到4个阶段公路段和OD的连通可靠性,如图6所示,以及各阶段的关键单元,见表10。图6a中,公路段S1和S4的连通可靠性无变化,原因在于各阶段被修复的关键单元不是其组成部分。公路段S2(LL)、S2(RL)、S3(LL)、S3(RL)和S5的连通可靠性有很大的改善,它们的连通可靠性在阶段4或之前已恢复至1。图6b中,所有OD的连通可靠性快速提升,在阶段4都达到了1,也就是恢复到了最佳连通状态。基于图6b中OD的连通可靠性,其恢复率可表示为:

表10 各阶段的关键单元Tab.10 Critical units in each period
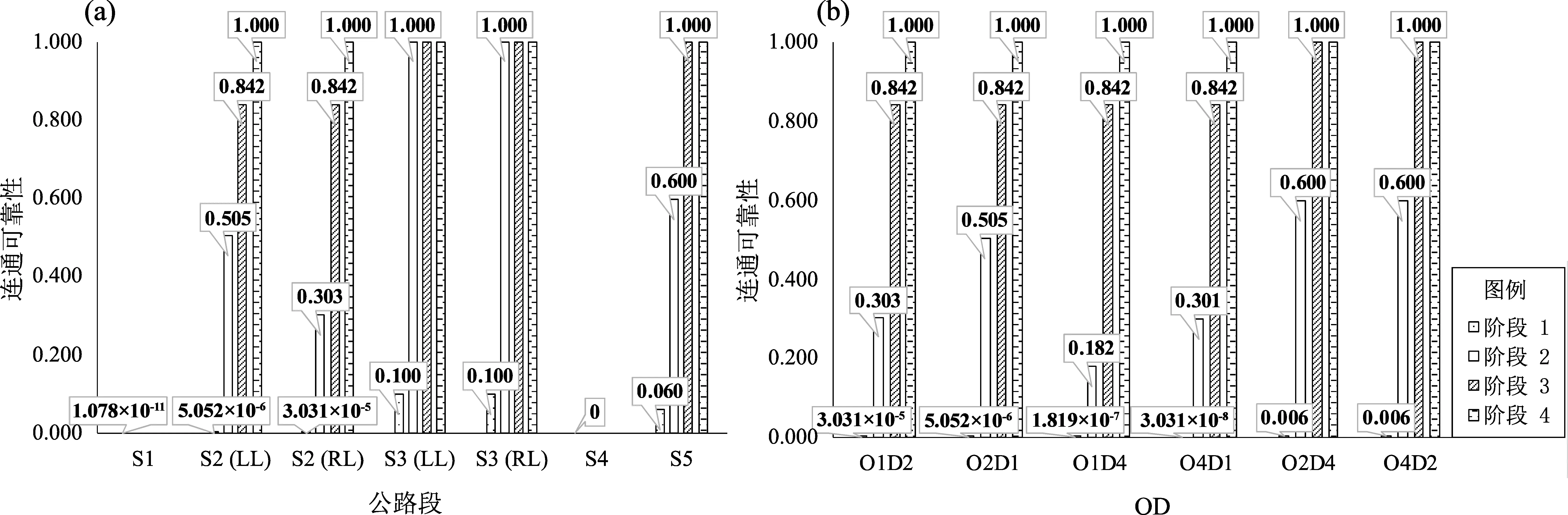
图6 各阶段公路段(a)和OD(b)的连通可靠性Fig.6 Connectivity reliability of highway segments(a)and OD pairs(b)in each stage

(8)
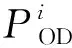
在表11中,阶段2的OD连通可靠性恢复率最高,后续阶段的恢复率逐渐降低。这说明修复阶段1的关键单元能够大幅提升OD的连通可靠性,所以在修复顺序上具有最高优先级,之后依次是阶段2和阶段3识别出的关键单元。对应表10中,阶段1识别的关键单元首先修复,之后依次为阶段2和阶段3识别的关键单元。所以决策者可以获得关键单元的修复优先级,从而实现区域公路网连通可靠性的恢复。

表11 OD连通可靠性的恢复率Tab.11 Recovery rate of OD connectivity reliability (%)
4 结论
区域公路网震后连通可靠性分析和系统功能恢复在应急响应阶段至关重要。本文采用经验预测方法计算得到公路单元的抗震可靠性,通过事件树和成功树分析构建区域公路网对应的贝叶斯网络,并将单元的抗震可靠性作为贝叶斯网络的先验概率输入,建立了区域公路网连通可靠性分析模型;根据敏感度分析和贝叶斯更新,提出关于系统功能恢复的启发式方法。将该方法应用于汶川地震中的实际区域公路网,得到如下结论:
(1)区域公路网连通可靠性分析模型建立起路段、桥梁、隧道和边坡单元结构破坏和公路网连通功能之间的联系,可根据公路单元的实际状态实时更新公路网的连通可靠性。
(2)基于贝叶斯更新的启发式方法识别出的关键单元及其修复优先级,能够促进区域公路网连通可靠性的快速恢复。
