城市供水管网震后修复策略研究*

龙 立，郑山锁，杨 勇，周 炎

(1.成都大学 建筑与土木工程学院，四川 成都 610106；2.西安建筑科技大学 土木工程学院，陕西 西安 710055；3.西北综合勘察设计研究院，陕西 西安 710003；4.三峡大学 土木与建筑学院，湖北 宜昌 443002)

0 引言

破坏性地震作用下，供水管网往往会由于节点破坏或管体断裂等造成大量用户节点功能失效，导致管网系统功能部分或全部失效，无法保证灾区消防、医疗及灾民生活用水，甚至引发次生灾害和流行疾病，造成二次伤害。因此，制定管网震后修复决策，使管网供水能力快速恢复至震前水平尤为重要。

近年来，国内外学者分别比较了水泵更新方案、水泵运行方案、泵站和储水罐运行方案等不同方案对管网震后供水能力的影响，主要侧重于恢复水泵、储水罐等组件以提升管网供水能力等(Chang，Shinozuka，2004；Cimellaro，2016；Zhao，2015；Zhuang，2013；Davis，2014；Tabucchi，2010；Farahmandfar，2017)。相较于水泵、储水罐等组件，管线在地震作用下更容易遭受破坏，管线修复顺序是确保供水管网功能高效恢复至震前水平的关键。目前，国内外学者对震后供水管线修复均有研究，如Liu等(2020a，b)以绵竹市供水管网为例，比较了基于静态重要度、损伤度和距离的3种管线修复顺序，认为静态重要度策略更有助于提高管网供水能力。贺金川等(2019)建立了以修复决策指数为指标的管网节点功能修复顺序决策模型，并以修复费用为衡量指标，对不同修复方案进行对比，给出了最优修复方案。程鹏(2013)将震后管网修复分为抢修严重破坏管线阶段、维修中等破坏管线阶段和检修轻微破坏管线阶段，每一阶段以管网可恢复度最大化原则选取受损管线进行修复，以实际管网为例，给出了不同烈度下管网的最优修复顺序，但忽略了震后抢修队伍的优化调度问题。Osman等(2017)建立了基于遗传算法的管线抢修队伍优化调度模型，最大限度地降低了修复时间、成本及对用户的影响程度。韩朝(2016)建立了以修复时间最短、失效节点损失最小为目标，修复可靠性最大为约束的多目标抢修队伍指派模型，利用两阶段求解方法给出了抢修队伍优化调度方案。破坏性地震作用下，关于供水管网管线会同时出现大量渗漏和爆管且应急抢修资源有限时，如何进行管网修复及抢修队伍调度的研究却鲜有报道。鉴于此，本文考虑震后管网中完好、渗漏和爆管管线共存及用户节点流量随水压变化的实际状态，首先建立供水管网水力满意度与重要度指标，然后提出在有限的应急抢修资源下供水管网的震后两阶段修复策略，进而针对第二阶段管网抢修数量较大的问题，提出抢修队伍多目标优化调度模型，并采用遗传算法对多目标优化调度模型进行求解，最终给出震损管网的最佳修复顺序及抢修队伍调度方案。

1 供水管网水力满意度与重要度

1.1 节点水力满意度

供水管网管线发生渗漏或爆管时，供水管网处于低压运行状态，用户节点流量受节点水压的影响，随着节点水压的下降，节点出流量减少甚至处于断水状态。本文定义震后节点水力满意度为震后节点水压与需求水压的比值：

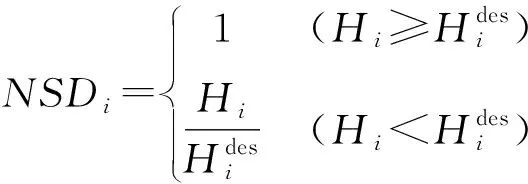
(1)

1.2 管网水力满意度

定义供水管网水力满意度为全部节点水力满意度的加权和：

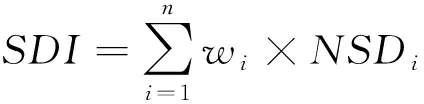
(2)

1.3 震损管线水力重要度

地震前、地震时及地震后，管网震后水力满意度通常采用如图1所示的曲线进行描述。图1中、、分别表示地震发生时、管网修复工作开展时及恢复至震前水平时的时间点。管网正常运行时，为常数1；地震发生时，立即下降至。通常被视为系统的地震吸收能力(Liu，2020)，可通过增强系统的健壮性和冗余性来提高。～为应急响应阶段，包括抢修方案制定及抢修资源准备等；随着抢修工作的开展，值逐步上升，直至恢复至震前水平。

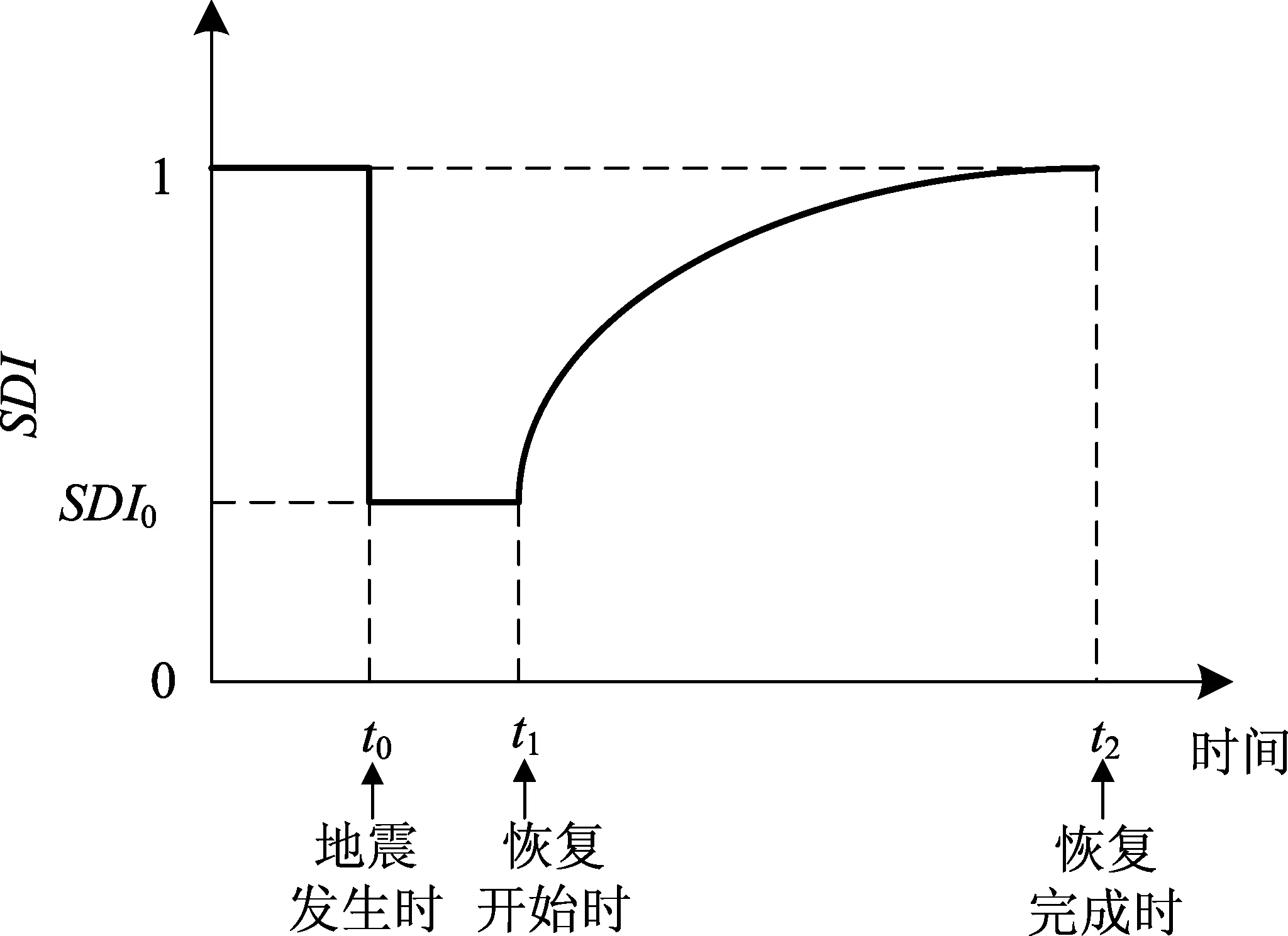
图1 供水系统水力服务满意度-时间曲线示意图Fig.1 Schematic diagram of the service satisfaction-time curve of water supply system

定义供水管网系统的抗震韧性指数为：

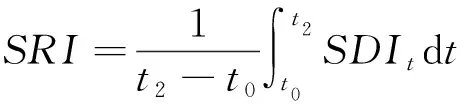
(3)

由图1可知，的取值范围为0～1。对于同一个供水管网，震后采用的管线抢修顺序越合理，所用恢复时间越短，对应时间点的值越大，则越大。因此，有助于量化管网故障管线抢修顺序的有效性。为了获得较高的实时值，本文引入水力静态重要度和水力动态重要度的概念，以表征管线修复引起的的增加量。

管线的水力静态重要度s，为：

s，=-

(4)

式中：为仅抢修管线后供水管网的；是全部震损管线均未抢修时的。

管线的水力动态重要度d，为：

d，=d,-

(5)

式中：d，是管线抢修后基于最新拓扑网络的供水管网的；是管线抢修前供水管网的。

2 供水管网震后修复策略

震后应急阶段，管网修复的首要目的是以尽可能短的时间最大限度地提升供水管网值，保障伤员和居民的医疗及生活用水，然而实际抢修工作中，由于抢修资源和人员有限，不可能同时对全部震损管线进行修复。因此，本文将供水管网震后抢修工作分为两个阶段：第一阶段对爆管管线进行抢修；第二阶段对渗漏管线进行抢修。

第一阶段的首要任务是保证尽量多的用户节点供水。相比于水力静态重要度，水力动态重要度考虑了已修复管线对剩余未修复管线的水力影响，可获得更为精确的重要度指标值，因此，本阶段采用该指标作为管线的重要度指标。首先修复与孤立节点相连的爆管管线，当孤立节点消除后，继续修复剩余爆管管线。每轮水力动态重要度确定后，仅修复该轮水力动态重要度最大的管线。经过多轮水力动态重要度计算后确定抢修顺序，对待修管线中优先级最高的管线，调度抢修时间最短的空闲抢修队伍对其进行修复；重复此过程，直至全部抢修队伍均被安排抢修任务；完成上一轮抢修任务的空闲抢修队伍，继续对剩余待修管线中优先级最高的管线进行修复，如此反复，直至所有爆管管线抢修完成。

第二阶段以值提升最快为原则。由于破坏性地震中渗漏管线的数量远大于爆管管线的数量，如果仍采用水力动态重要度进行衡量，将耗费大量的计算时间，严重影响管网的抢修进程，而采用水力静态重要度时，在大幅度提高计算效率的同时仍能获得较高值。因此，本阶段采用该指标作为管线重要度衡量指标。由于需修复的管线数量较多，抢修队伍需在渗漏管线间多次迁移，增加了管网修复的时间和成本。为了更好地调度宝贵的抢修资源，本文建立了综合考虑管网水力恢复指数、抢修时间和抢修成本的多目标优化调度模型，并采用遗传算法对其进行优化，寻找较优的调度顺序，以较低的时间和成本，获得较高的。

3 抢修队伍多目标优化调度模型

抢修队伍多目标优化调度模型涵盖了管网水力恢复指数最高、修复时间最短和修复费用最低的3个互相冲突的目标函数。

3.1 管网水力恢复指数模型

定义管网水力恢复指数为全部渗漏管线的水力静态重要度与顺序重要度系数的乘积的累加和：

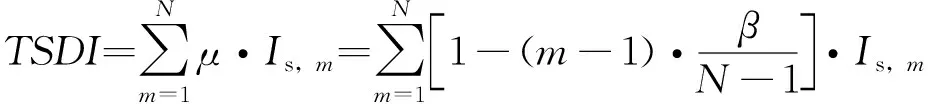
(6)

式中：为管线抢修顺序的重要性系数，抢修顺序越靠前，越大；为渗漏管线总数；为管线的抢修顺序；s，表示抢修顺序为的管线的静态水力重要度；为重要性系数差值，决定渗漏管线间的差值，本文统一取0.3。

需说明的是，计算管网水力恢复指数模型时，需对震损管网进行水力分析。本文考虑震后管网管线完好、渗漏和爆管共存的实际状态，同时考虑了震后用户节点流量随水压的变化，编制了水力计算程序，为管网震后修复决策分析提供了技术支撑。其中渗漏模型(刘鹤年，2008；邹日清等，2018)、爆管模型(侯本伟，2014)和节点压力驱动模型(Gupta，Bhave，1996；何丽荣等，2018)参考国内外已有研究成果。

3.2 修复时间模型

供水管网震后渗漏管线修复花费的总时间包括渗漏管线修复时间和抢修队伍在抢修点间位置迁移时间两部分，管网修复完成时，耗时最长的队伍所使用的时间即为抢修总时间，表示为：

=max(+) (∈)

(7)

式中：为抢修队伍数量；为抢修队伍的总抢修时间；为抢修队伍的位置迁移时间。

抢修队伍的总抢修时间为：

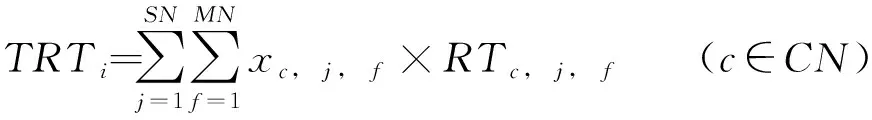
(8)

式中：， ， 为二进制变量，当抢修队伍使用抢修方法修复渗漏管线时，其值为1，否则为0；， ， 为抢修队伍使用抢修方法修复管线花费的时间；为抢修队伍数量；为渗漏管线数量；为抢修方法数量。

在建立抢修队伍位置迁移时间模型前，本文引入抢修步骤的概念表示渗漏管线由指定抢修队伍修复的顺序。抢修步骤的数量为向上取整。对于抢修队伍，完成一根渗漏管线抢修后，需按照既定的抢修步骤前往下一根渗漏管线进行抢修，抢修步骤结束之后所花费的位置迁移时间之和即为抢修队伍的位置迁移总时间：

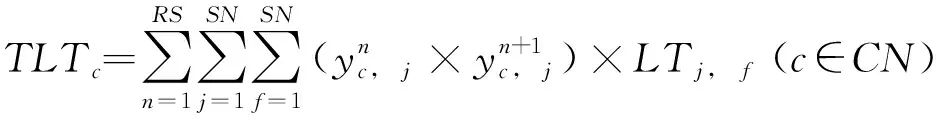
(9)

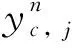
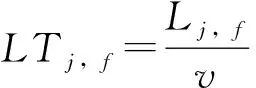
(10)

式中：， 为故障管线和之间的最短路径距离；为位置迁移速度，主要与发震时间、地震强度、沿街建筑物倒塌情况等因素有关(赵晶晶，2016)，可表示为：

=0578

(11)

式中：为发震时间对车速的影响系数；为建筑倒塌对车速的影响系数；为城市平均行车速度。

3.3 修复费用模型

定义修复费用总成本为，包括渗漏管线抢修费用和抢修队伍位置迁移费用：

=+

(12)

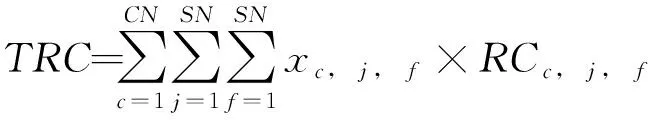
(13)

式中：， ， 为二进制变量，当抢修队伍使用抢修方法修复渗漏管线时，其值为1，否则为0；， ， 为抢修队伍使用抢修方法修复渗漏管线花费的费用。

供水管网每处破坏管线的抢修费用， ， 采用《地震现场工作第4部分：灾害直接损失评估》(GB/T 18208.4—2011)所提出方法进行计算：

， ， =+

(14)

式中：为管线维修直接费，包括机械费、破路费、材料费(元)等；为人工费(元)；为季节影响系数，冬季施工时取1.1，其他时间施工取1.0。其中，材料费、人工费用与管径有关，机械费、破路费与管径及管线破坏处的道路类型有关，参照杨丹(2011)研究结果取值。

定义为管网修复完成时所有抢修队伍花费的位置迁移成本：

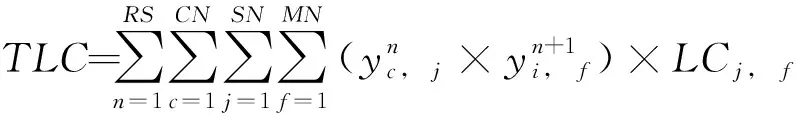
(15)

式中：， 为抢修队伍在渗漏管线和之间的位置迁移成本；其它参数同式(9)。

3.4 多目标优化调度模型

基于上述单目标优化模型的目标函数，采用线性加权法构建渗漏管网抢修队伍多目标优化调度模型的目标函数为：

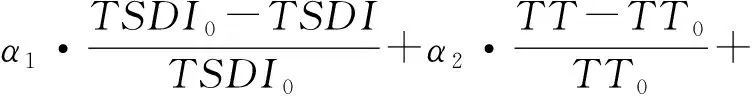
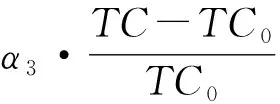
(16)

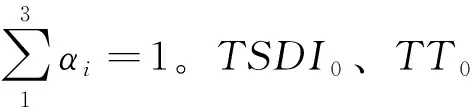
本文多目标优化调度模型的主要约束是管网水力平衡约束，需满足节点流量连续性方程、管线压降和能量方程。

4 基于遗传算法的多目标优化调度算法

遗传算法的计算步骤包括编码、生成初始种群、适应度函数选取、选择操作、交叉操作和变异操作等。图2给出了采用遗传算法求解抢修队伍调度多目标优化模型的染色体结构及模型间的调用关系。具体实施流程如下：

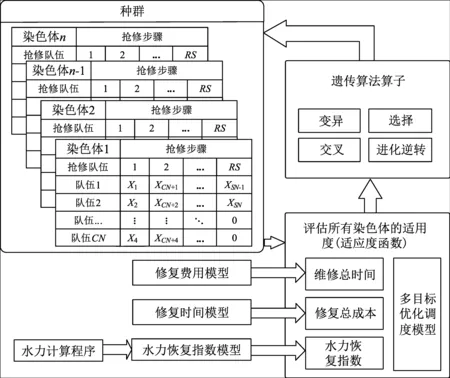
图2 染色体结构和遗传算法优化流程Fig.2 Chromosome structure and optimization process of genetic algorithm

①编码：采用矩阵编码方式进行编码，矩阵维度为×，为抢修步骤数量，为抢修队伍数量，矩阵中的值为按顺序编码方式进行编码的各渗漏管线的编号，当=时，矩阵中每个位置均对应一个渗漏管线编号，否则，矩阵除了最后一列，其他列每个位置均对应一个渗漏管线编号，剩余的管线编号随机放入矩阵最后一列。假设、分别为12和4，则=3，矩阵维度为4×3(图3a)，管线编号为1～12。矩阵的每个位置对应一个数值，矩阵中2行3列的数值10表示当处于抢修步骤3时，抢修队伍2抢修的管线编号为10；假设、分别为13和4，则为4，矩阵维度为4×4(图3b)，管线编号为1～13。矩阵除了第4列，其它位置均对应管线编号，第4列的数值13表示处于抢修步骤4时，调度抢修队伍2抢修管线13，该列其它的数值0表示其它队伍无抢修任务。

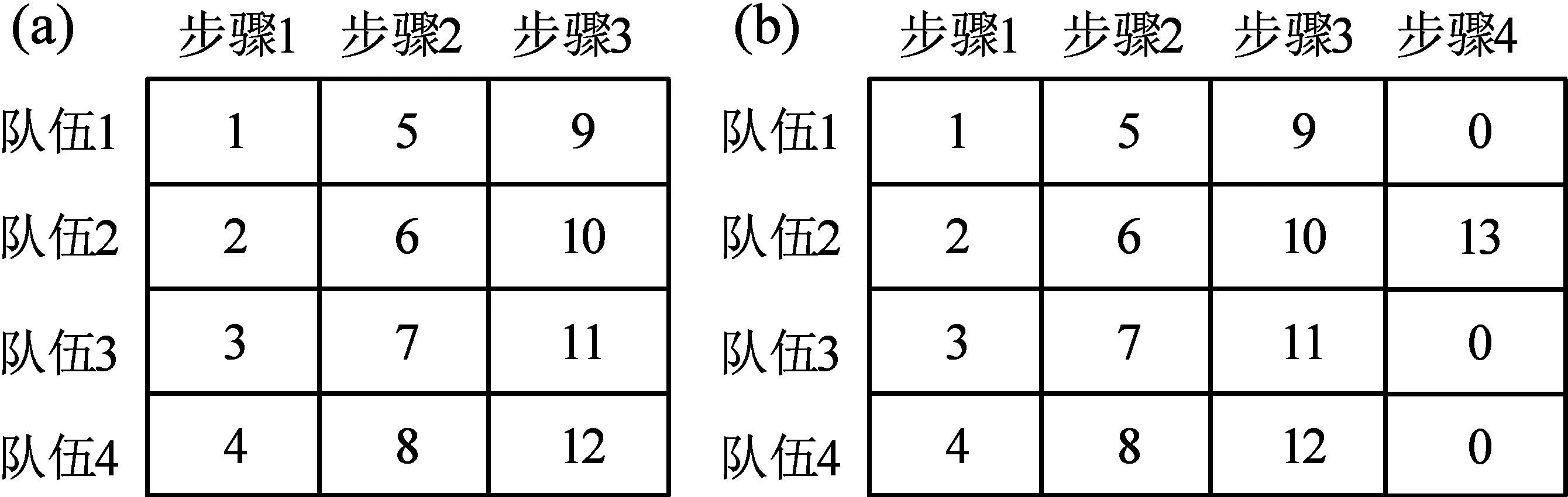
图3 矩阵维度为4×3(a)和4×4(b)染色体编码示意图Fig.3 Schematic diagram of chromosome encoding with a 4×3 matrix(a)and a 4×4 matrix(b)

②生成初始种群：根据、和的数量随机生成一个种群，种群中每个个体代表一种解决方案，每个解决方案代表各抢修队伍修复管线的顺序。

③适应度函数：取为目标函数的倒数。对于每种解决方案，根据式(6)、(7)和(12)分别计算、和，并将其代入式(16)计算多目标函数值，值越小，适应度越高，表明该解决方案所对应的个体是种群中更为优选的个体。

④遗传算子：本文采用适应度比例法作为选择算子，交叉算子采用两点交叉法。变异算子是一种简单的基因变异方式，将个体上的一个或多个基因座上的基因用其他等位基因代换，从而形成新的染色体。

⑤遗传算子操作完成后，生成包含新的解决方案的种群。重复步骤①～②，直到达到设定的收敛标准为止。

5 算例分析

本文采用的某小型供水管网共有40个节点，64根管线，管材均采用球墨铸铁，节点40为供水源点，水位恒定在60 m，供水量为840.41 L/s。该管网所处场地为II类场地，埋深均为2 m。管线水头损失采用Hazen-Williams公式计算，管线的粗糙系数均为130，各节点的流量、标高及各管线的管长和管径如图4所示。所有节点的设计最小水压和基准水压分别为0 m和15 m。假定Ⅸ度地震作用下管线1、4、38、62发生爆管破坏，管线3、8、12、16、21、24、27、32、36、44、46、49、50、53、57、60发生渗漏破坏，由4支抢修队伍分两阶段进行抢修。抢修队伍的抢修时间及成本如图5所示，抢修队伍在各故障管线之间位置迁移时间和成本如图6所示。

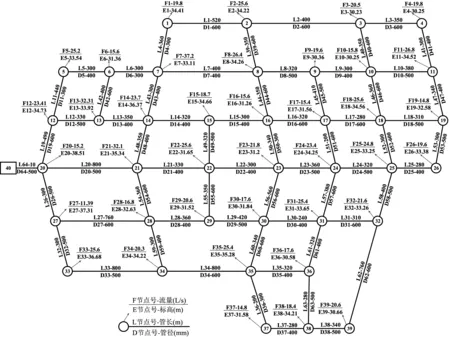
图4 城市供水管网图Fig.4 Map of urban water supply networks

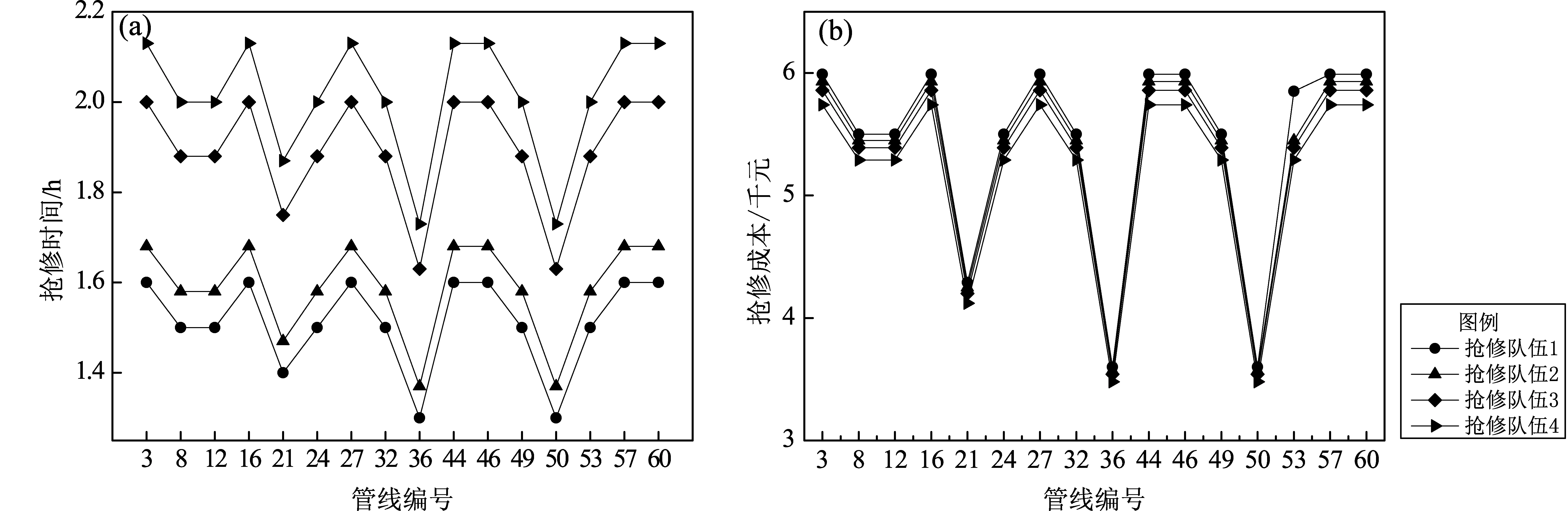
图5 抢修队伍修复不同管线花费的时间(a)和成本(b)Fig.5 Time(a)and cost(b)for rescues teams to repair different pipelines

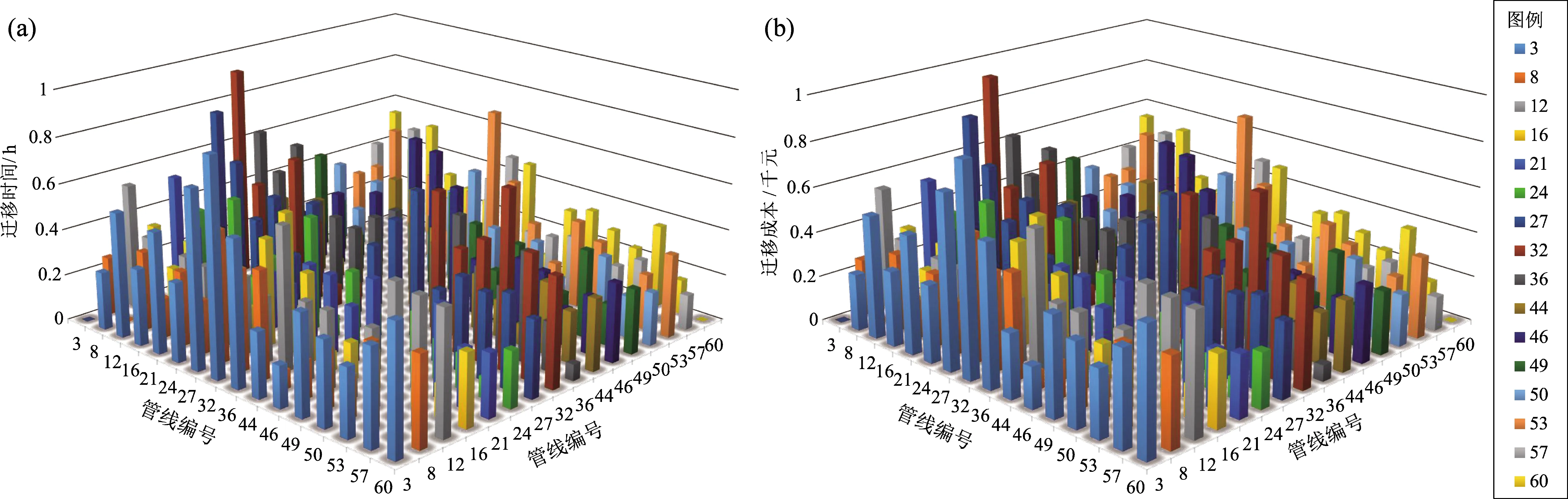
图6 抢修队伍在不同管线间位置迁移的时间(a)和成本(b)Fig.6 Time(a)and cost(b)for rescue teams moving between different pipelines

5.1 震后抢修第一阶段

管网中出现了孤立节点1和39，基于第一阶段抢修策略，优先修复震前管网中与孤立节点相连的管线，结合漏损管网的水力计算程序与管线水力动态重要度指标，计算得到第一阶段爆管管线的抢修顺序和抢修队伍调度方案见表1和表2。由表可知，管线抢修顺序为1-62-38-4，调度用时最短的抢修队伍优先对水力动态重要度高的管线维修。所有爆管管线修复完成后，共花费时间1.88 h，值恢复至0.45。

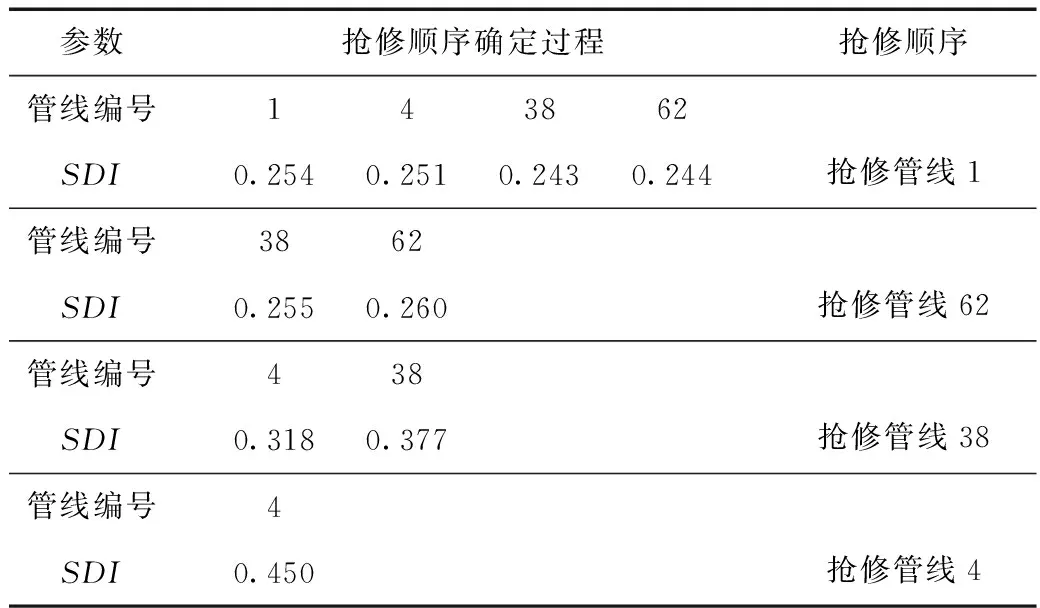
表1 爆管管线的抢修顺序Tab.1 Order of repairing the burst pipe

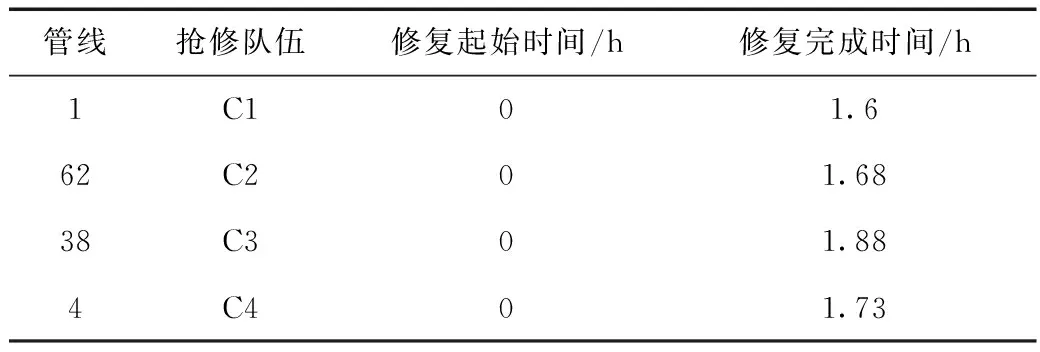
表2 震后第一阶段抢修队伍调度表Tab.2 Schedule of emergency crews in the first stage after the earthquake

5.2 震后抢修第二阶段

爆管管线抢修完毕后，剩余故障管线全部为渗漏破坏，管网抢修进入第二阶段，采用遗传算法分别对成本目标、时间目标和水力恢复指数进行单目标优化，其中，种群大小为100，最大遗传代数为400，交叉概率为0.9，变异概率为0.05。进而基于单目标优化结果进行多目标优化，优化程序采用Matlab实现。单目标及多目标优化结果、各优化方法的抢修调度方案见表3、4。

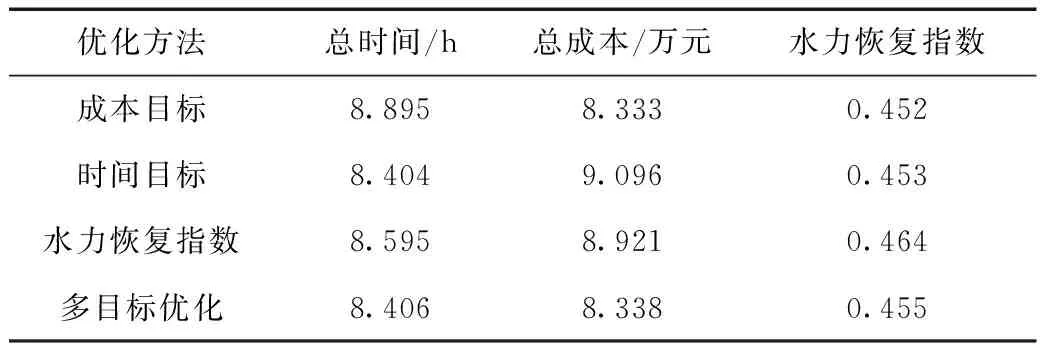
表3 单目标及多目标优化结果Tab.3 Results from the single-objective and multi-objective optimization

本文同时解决了4个不同的优化问题，结合表3和表4可以得出如下结论：不同优化目标获得的管线抢修顺序及抢修队伍调度方案差异较大。基于多目标优化模型计算得到的总时间、总成本及水力恢复指数与对应单目标优化模型的最优结果分别相差0.06%、0.03%、2%。与修复时间单目标方案相比，多目标优化方案在时间仅增加0.06%的同时节约了5.5%的总成本，水力恢复指数提高了0.6%；与修复成本单目标方案相比，多目标优化方案成本增加了0.03%，但时间节约了8.3%，水力恢复指数提高了0.29%；与水力恢复指数单目标优化方案相比，多目标优化方案水力恢复指数仅下降2%，但节约了6.5%的总时间和2.2%的总成本。多目标优化方案虽然不能获得单项最优结果，但综合结果最优。

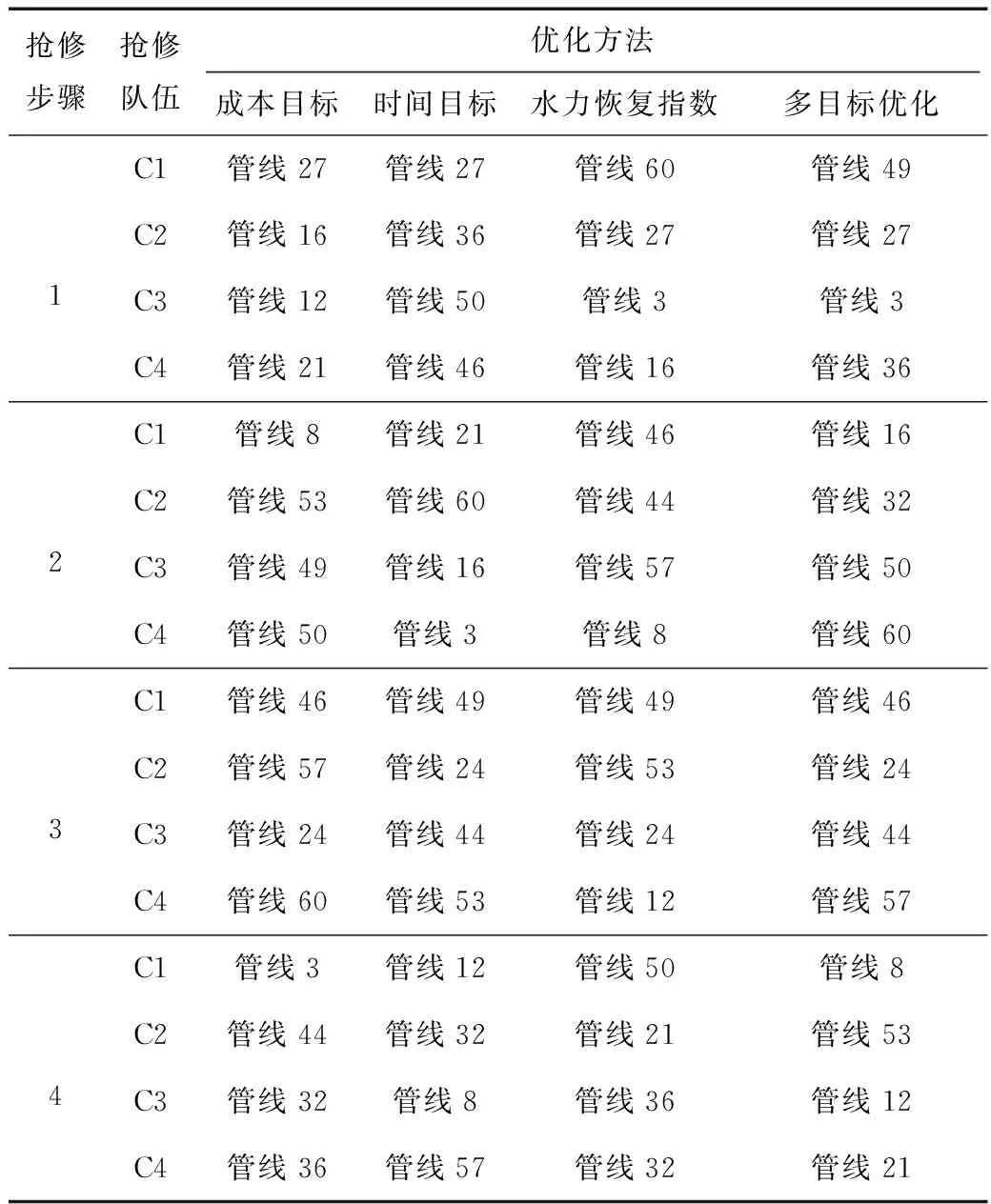
表4 不同优化方法抢修调度方案Tab.4 The emergency repair schedule with different optimization methods

由于震后修复的首要目标是恢复管网水力满意度，表5对比了基于水力恢复指数的最优方案(方案1)与多目标优化方案(方案2)修复过程中值随抢修时间变化的详细过程。由表5可知，方案1中管网值提升幅度较大，管线53修复完成后，管网值为1，恢复至震前供水水平，此时，已完成10根管线修复，所需时间7.97 h；方案2同样在管线53修复完成后，使管网值恢复至1，虽然比方案1多抢修1根管线，但抢修速度较快，所需时间为7.29 h，比方案1提前了40 min。图7给出了两种方案-折线图，由图可知，管网值恢复至1前，方案2每个时间点对应的值均大于方案1，且恢复所用时间更短，值更高，表明方案2的修复调度方案更优。

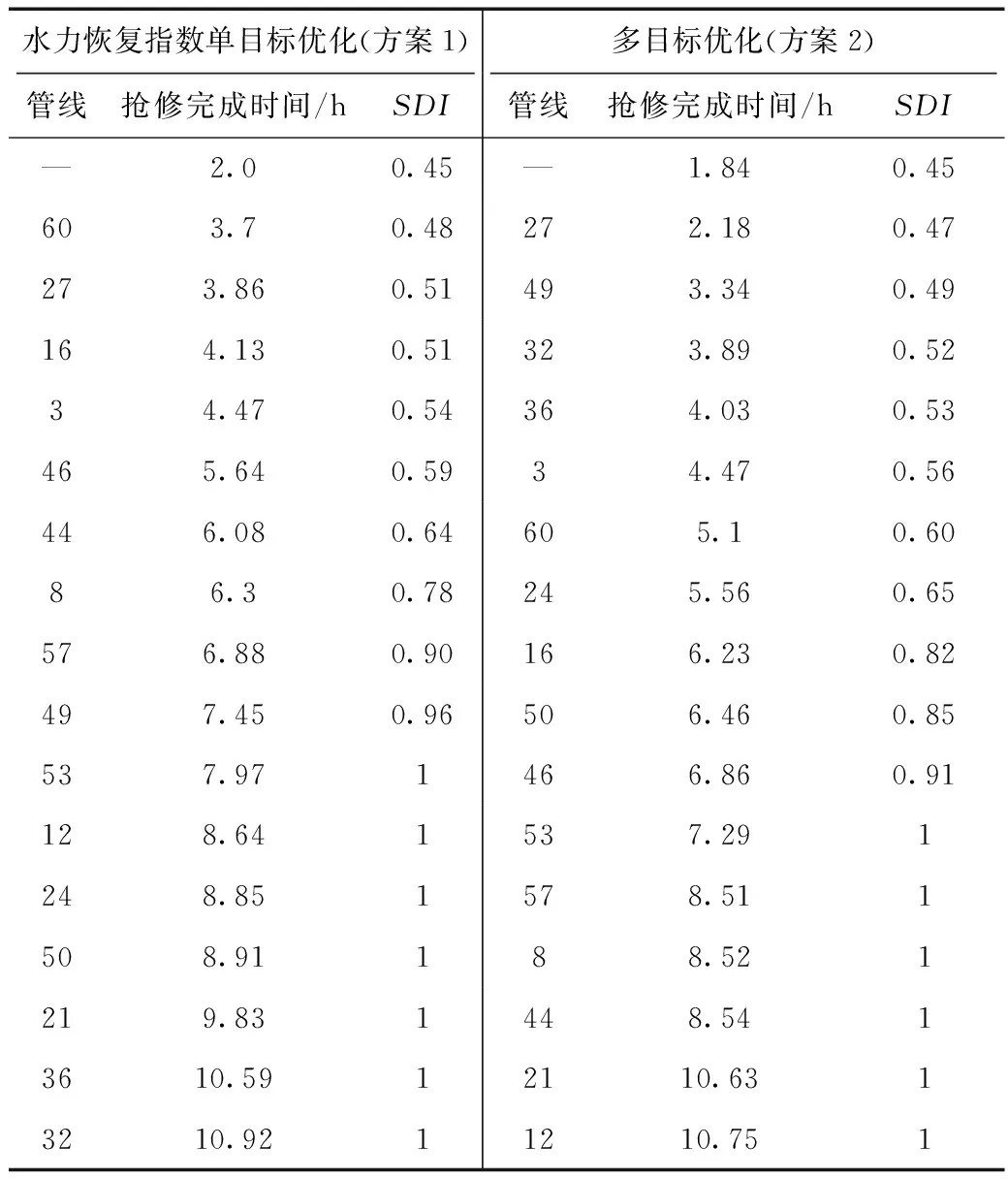
表5 抢修调度方案对应的SDI-t结果Tab.5 SDI-t results corresponding to the emergency repair schedule

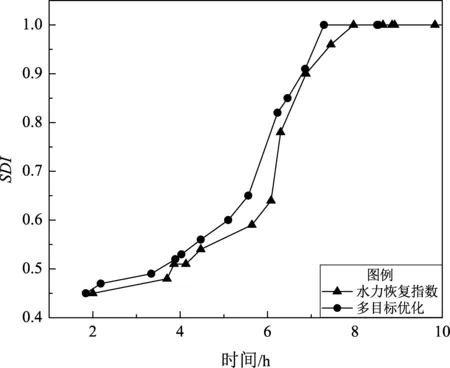
图7 基于水力恢复指数与多目标优化方法的SDI值对比Fig.7 SDI values based on the hydraulic recovery index and the multi-objective optimization

6 结论

本文提出了供水管网震后抢修两阶段优化调度策略，建立并编码实现了抢修队伍多目标优化调度模型，并将其应用于某小型供水管网进行算例分析，得出以下结论：

(1)第一阶段以水力动态重要度作为管线的重要度指标，优先修复爆管管线，保证了尽量多的用户节点供水。

(2)第二阶段以水力静态重要度作为管线的重要度指标修复渗漏管线，不同优化目标获得的管线抢修顺序及抢修队伍调度方案差异较大。基于多目标优化模型计算得到的总时间、总成本及水力恢复指数与对应单目标优化模型的最优结果分别相差0.06%、0.03%、2%。多目标优化方案虽然不能获得单项最优结果，但综合结果最优。

(3)基于多目标优化方案的管网水力满意度比基于水力恢复指数最优方案的管网水力满意度值恢复至1的时间更短，管网韧性指数更高，基于多目标优化的修复调度方案更优。

基于多目标优化的抢修调度方案是一种高效、低成本且能获得较高水力恢复指数的修复方案，可为震后开展供水管网抢修工作提供有力支撑。