基于震害率经验模型分析供水管道地震易损性*

王晓娜，郭恩栋，闫培雷，吴厚礼，金宇航，何润泽

(1.中国地震局工程力学研究所 地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080；2.中国地震局工程力学研究所 地震灾害防治应急管理部重点实验室，黑龙江 哈尔滨 150080)

0 引言

供水管道作为生命线系统的重要组成部分，是维持居民生活用水、医疗用水和消防用水等方面正常运转必不可少的基础设施(杨超，蒋建群，2011)。历史震害表明，地震会导致供水管道破坏而造成巨大的经济财产损失(张振鹏等，2013)。我国作为一个地震多发国家，采用综合手段减轻地震灾害风险是必由之路。地震保险是分散地震灾害风险的重要手段之一，体现为震前预防、震后补偿和救灾减损。然而，地震保险却在供水系统中举步维艰，其中一个重要原因在于缺乏适宜的基于连续地震动参数的供水管道易损性模型，用于分析供水管道在不同强度地震作用下的损失大小，进而确定合理的保险费率和赔付政策(刘如山等，2006)。因此，建立合理的基于连续地震动参数的供水管道地震易损性模型对地震保险至关重要。

国内外供水管道地震易损性研究方法运用较为广泛的是经验统计法和有限元分析法，且得出了不同的易损性模型。如王立功等(1985)基于海城、唐山等城市的供水系统震害经验，综合考虑管材、管径、管道接口等影响因素，给出了管网易损性指数。Liu等(2020)考虑了管道易损性水平和易损性指标之间的随机性和非线性，基于分形理论，建立了供水管道地震易损性分形插值函数模型。何双华等(2012)考虑了供水管网的拓扑位置和水力因素，基于突变级数法并结合网络脆弱性评估方法和相对量化法，给出了供水管网的地震易损性风险等级划分。王书锐(2019)通过对经过CIPP加固前后的DN150球墨铸铁管进行实验研究，结合增量动力分析法，给出了DN150球墨铸铁管基于的地震易损性曲线。Chen等(2014)结合Abaqus有限元建模和Fuzzy数学理论，建立了供水管网地震易损性评估模型。

目前供水管道的研究成果主要是管道地震破坏评估模型和震害率模型，无法满足我国地震保险中用于评估供水系统地震经济损失的基于地震动参数的易损性模型的需要。鉴于此，本文基于供水管道震害率经验统计模型，结合供水管道破坏等级划分，给出了不同材质管道在5种不同破坏等级下发生的概率与地震强度之间的关系，计算出不同地震强度下的损失率，从而更好地评估地震造成的供水管网直接经济损失。

1 震害率经验统计模型

供水管道震害率经验统计模型的核心评估指数是管道震害率(单位：处/10 km)，为此，国内外学者结合历史管道震害资料，综合考虑影响管道地震破坏的内部参数(管材、管径、接口形式等)和外部参数(地震动、场地条件等)，基于统计方法分析得到了管道震害率的估算公式(Shinozuka，1981；Hwang，1998；American Lifeline Alliance，2001；日本水道协会，2009；孙晨雨等，2018)，这些方法以管道单位长度内的破坏处数来反映管道的震害情况(American Lifeline Alliance，2001)。供水管道震害率经验统计模型不仅划分了五种破坏等级，还通过考察并收集大量的国内管道实际震害资料，建立了Ⅵ～Ⅸ度地震烈度下6种管道的震害率模型。

1.1 破坏等级划分

供水管道的地震破坏维修一般以破坏处数为单位，且通常用单位长度内管段破坏处数来衡量管道的破坏程度，故将管道震害率作为破坏等级划分标准依据是合理的。2009年我国颁布的国家标准《生命线工程地震破坏等级划分》(GB/T 24336—2009)规定了供水系统中供水管道的地震破坏等级划分标准，不同破坏等级管道震害率取值见表1。

表1 不同地震破坏等级供水管道震害率λTab.1 Damage rate λ of water supply lines at different earthquake damage levels

1.2 震害率经验统计模型

在众多供水管道震害破坏影响因素中，除了地震强度之外，管材无疑是最大影响因素。因此，研究不同管材供水管道的地震易损性，不仅能在管网建设和改造工程中的管材选择问题上有重要指导意义，也有利于供水管网保险费率的厘定。

郭恩栋等(2012)通过收集大量的2008年汶川8.0地震时供水管道震害资料，结合王东炜(1991)的研究结果，提出了现役地下管道震害率模型，见表2。

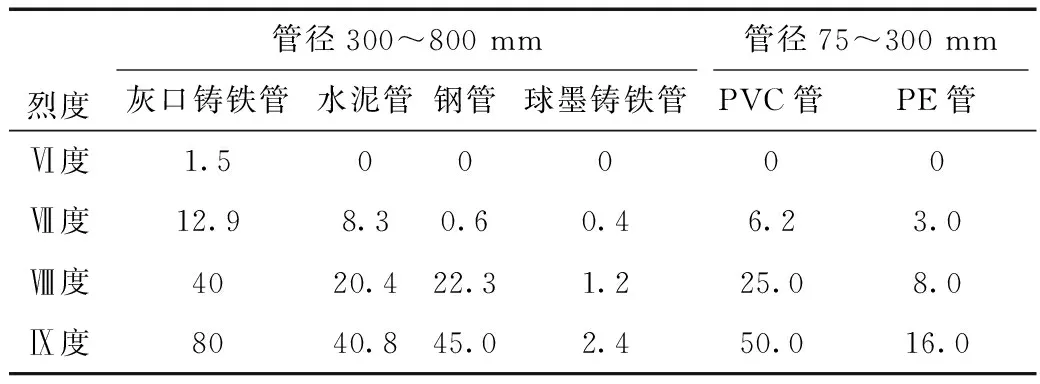
表2 现役地下管道震害率模型Tab.2 Model of seismic damage rate of the active underground pipeline

2 地震易损性评估方法

2.1 地震易损性曲线

假定一定长度管道在地震作用下发生的破坏处数服从离散型泊松分布(国艳，王晓青，2010；刘智等，2013；杨舒云等，2018)，如：

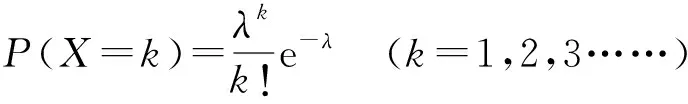
(1)

式中：泊松分布参数为通过经验公式或者大量统计震害资料得到的平均震害率；为管道破坏处数，则(=)为管道发生处破坏的概率。

借助式(1)，并结合表1中破坏等级划分计算供水管道在不同破坏等级发生的概率，即地震易损性矩阵。为了得到平均震害率下某确定管道的易损性曲线，需要将破坏概率转化为某一地震强度下的超越概率：

(2)

式中：为地震强度；为破坏等级，规定越大破坏等级越低；故()为地震强度下的供水管道在破坏等级发生的概率；′()为地震强度下的供水管道在破坏等级的超越概率。

双参数对数正态分布函数(贺思维等，2018)为：

(3)

式中：()为供水管道在第个破坏等级的超越概率；为地震动值；(*)为正态分布函数；和分别为供水管道在第个破坏等级的中位值和对数标准差。

由式(2)可知，在任何地震强度下，基本完好的超越概率均为1，故基本完好的易损性曲线无需考虑。得到超越概率矩阵之后，利用式(3)拟合得到某确定管道平均震害率下的不同破坏等级超越概率与地震强度间的关系。

2.2 地震损失率

本文对不同破环等级发生概率与相应破坏等级损失比中值的乘积进行求和，得到供水管道地震损失率：

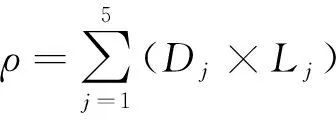
(4)

式中：为管道地震损失率；为管道发生破坏等级的概率，规定越大破坏等级越低；为管道发生破坏等级对应的损失比，规定越大破坏等级越低。

各破坏等级概率由地震易损性曲线可知：基本完好的概率为1与轻微破坏超越概率的差值；轻微破坏的概率为中等破坏的超越概率与轻微破坏的超越概率的差值；中等破坏的概率为严重破坏的超越概率与中等破坏的超越概率的差值；严重破坏的概率为毁坏的超越概率与严重破坏的超越概率的差值；毁坏的概率为毁坏的超越概率。供水管道在不同破坏等级对应的损失比中值见表3。当供水管道破坏等级为基本完好时，表示基本功能不受影响，无需修复，即破坏等级为基本完好时视作没有损失，损失比取为0；当破坏等级为毁坏时，代表损毁严重，不再具有修复价值，需要重建，因此损失比取为100%(李玉芹，2020)。

表3 供水管道在不同破坏等级的损失比(单位：%)Tab.3 Ratio of earthquake damage losses of water supply lines subjected to difterent damage levels(unit：%)

3 地震易损性分析

3.1 易损性曲线

本文以PE管为例，利用供水管道地震易损性评估方法给出相应的易损性曲线。PE管在式(1)中值和值取值见表4、5，由此得到的PE管的地震易损性矩阵和超越概率矩阵分别见表6、7。

表4 PE管在不同地震烈度下的λ值Tab.4 λ-value of PE pipes subjected to different earthquake intensities

表5 PE管在不同破坏等级的k值Tab.5 k-value of PE pipes subjected to different damage levels

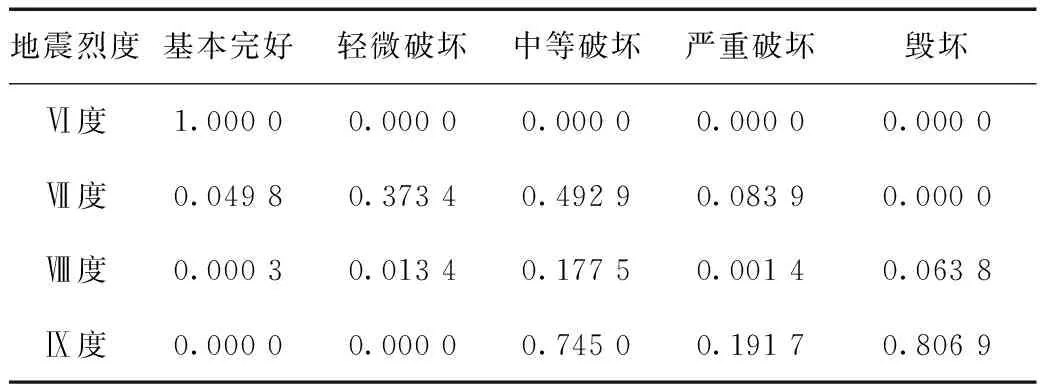
表6 PE管地震易损性矩阵Tab.6 Seismic vulnerability matrix of PE pipes

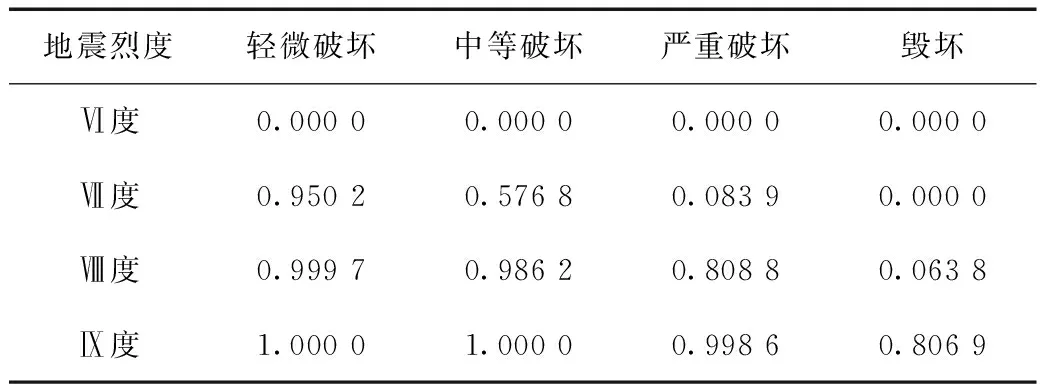
表7 PE管超越概率矩阵Tab.7 Exceedance probability of PE pipes

利用双参数对数正态分布函数对表7进行拟合，得到PE管的地震易损性曲线。同理可得到其他5种管道的地震易损性矩阵和超越概率矩阵，拟合后也可得到各自的易损性曲线及参数。6种管材的供水管道的拟合参数见表8，地震易损性曲线如图1所示。

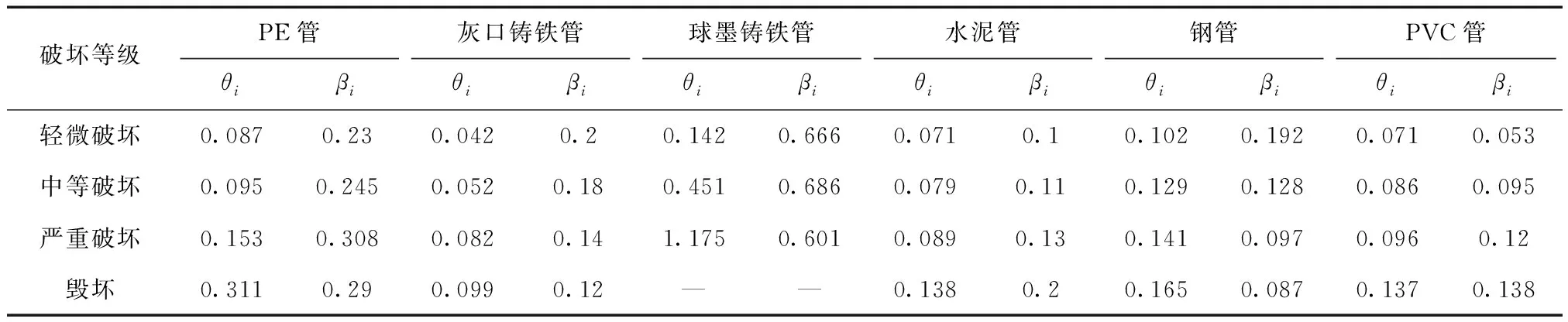
表8 PE管易损性函数中位值θi和对数标准差βiTab.8 Median values and standard deviations of vulnerability function of PE pipes

图1 不同管材供水管道地震易损性曲线Fig.1 Seismic vulnerability curves of different water supply lines

3.2 易损性曲线拟合优度检验

本文采用分布对以上得到的供水管道地震易损性曲线进行拟合优度检验，以易损性矩阵中各破坏等级的超越概率为观测值，以通过双参数对数正态分布拟合得到的各破坏等级的超越概率为理论值，通过统计量式(5)比较观测值和理论值的差异，利用这一比较来评价拟合优度，具体如下：

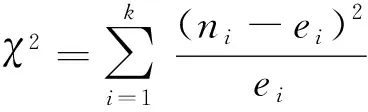
(5)

式中：为观测值数量；为观测值；为理论值；给定显著性水平，则1-， 为分布在概率分布值(1-)处的临界值，=-1为自由度，如果满足：

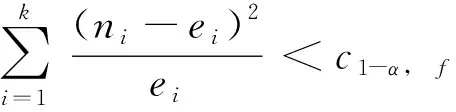
(6)

则说明假定的理论分布在显著性水平下可以接受，反之则认为现有数据不支持该假设分布。要求得到的供水管道地震易损性曲线能通过具有95%置信率的拟合优度检验，故本文取=0.05，则=7.814 1。

由表9可知，PE管地震易损性拟合优度检验结果满足式(6)，同理可对其余5种管材供水管道地震易损性曲线进行拟合优度检验，结果表明本文绘制的6种管材供水管道地震易损性曲线均可通过具有95%置信率的拟合优度检验。

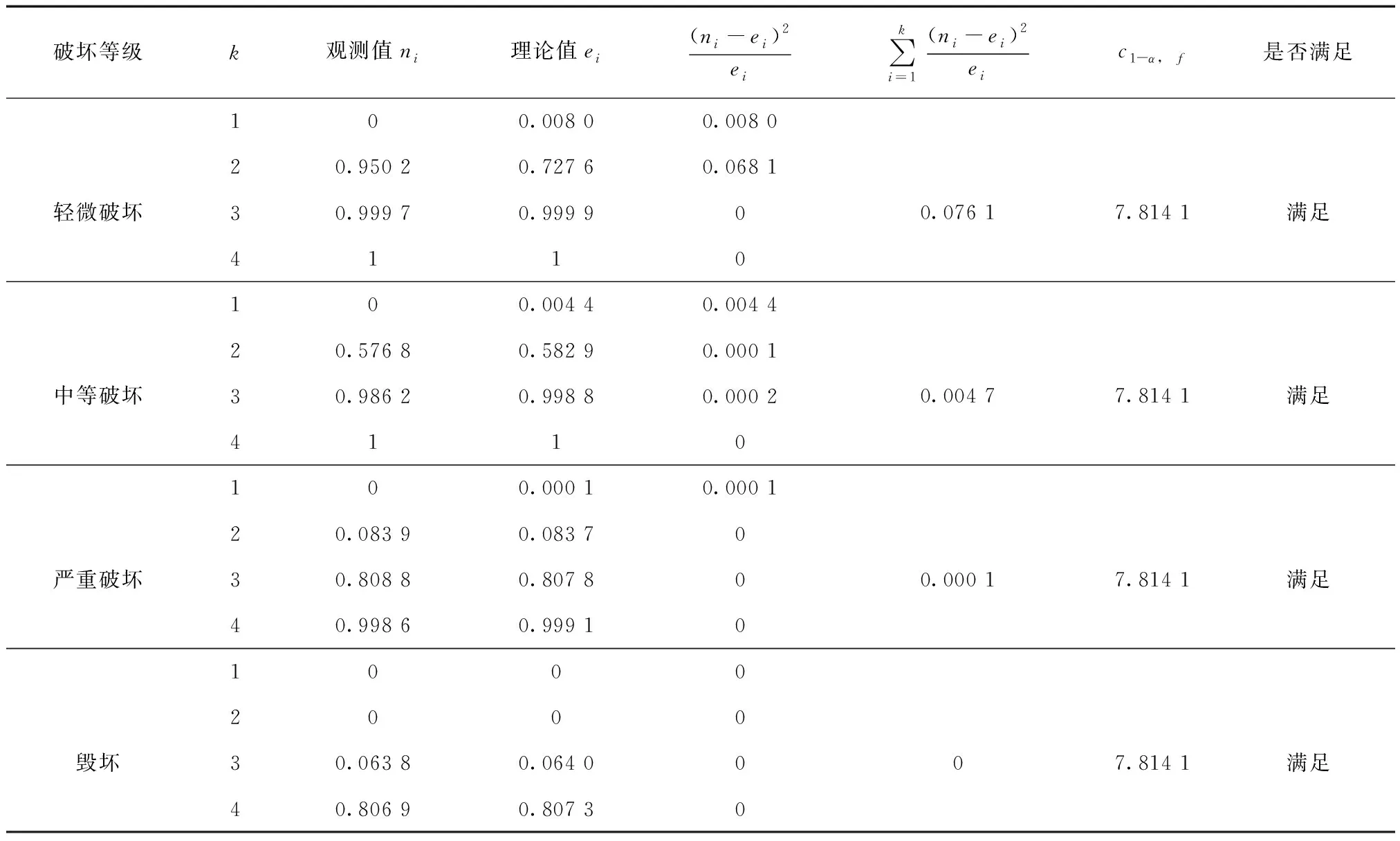
表9 PE管地震易损性曲线拟合优度检验Tab.9 Test of goodness of fit of the seismic vulnerability curve of PE pipes

3.3 损失率比较

求解供水管道损失率除了本文所采用的方法之外，还有孙晨雨等(2019)提出的生命线工程直接经济损失预测改进算法(以下简称“改进算法”)，两种方法不同之处在于前者是基于地震易损性曲线，后者是基于震害率，将震害率和损失比进行线性插值计算。

因此，为了进一步检验本文得到的地震易损性曲线的合理性及准确性，将基于本文绘制的供水管道地震易损性曲线，结合传统损失率求解方法得到的地震损失率和基于震害率直接求解的地震损失率(改进算法)进行比较，如图2所示，并将两种方法得到的Ⅵ～Ⅸ地震烈度下的损失率进行比较，见表10。

图2 两种方法得到的不同管材供水管道地震损失率曲线比较Fig.2 Comparison of curves of the seismic loss rate of different water supply pipes by two mehods

表10 不同地震烈度下两种方法得到的损失率比较Tab.10 Comparison of the loss rates subjected to a certain earthquake intensity by two methods

由图2可知，两种方法得到的地震损失率曲线变化趋势基本相同，且灰口铸铁管、球墨铸铁管和PVC管3种管道的损失率曲线几乎重合。由表10可知，除了在Ⅶ度地震烈度下，两种方法所得球墨铸铁管损失率相差7.8%，钢管损失率相差6%外，其余情况的管道损失率相差均在2%以下。

4 结论

本文基于震害率经验统计模型，结合泊松分布得到了6种管材供水管道连续的地震易损性曲线，并使用基于地震易损性曲线、结合传统损失率求解方法得到了地震损失率。将本文得到的地震损失率和基于震害率所得到的地震损失率进行比较，结果表明两种方法所得结果基本一致，说明本文绘制的供水管道地震易损性曲线合理准确。本文研究结果对管道建设和改造工程中管材的选择具有指导意义，也可为保险行业供水管网的地震经济损失分析提供支撑。

本文研究结果主要是基于2008年汶川8.0地震供水管道的震害资料取得的，对四川省的适用性较好，但推广到我国其它地区具有一定的局限性。除此之外，本文钢质供水管道的易损性结果是基于敷设时间较长、腐蚀较严重的钢管道震害率数据得到的，而没有腐蚀的、新敷设钢管抗震性能会更好。因此，本文的结果在应用到保险等领域时还应该适当考虑敷设时间以及腐蚀程度等因素的影响。