极值点偏移问题的解法探究——从对数平均不等式谈起

梁昱韬

(江苏省苏州中学高二(17)班，215007)

高中导数题中有这么一类题,它们既复杂多变,又有规可循;既形式花哨,又本质归一,这便是极值点偏移问题.此类问题的解决方法多样,本文从对数平均不等式谈起,由浅入深地讨论此类问题的一类解法.

一、千呼万唤始出来,犹抱琵琶半遮面

结论对任意两个不同正实数a,b,恒有不等关系(对数平均不等式)

①

二、纸上得来终觉浅,绝知此事要躬行

我们首先通过一道例题求解,感受应用对数平均不等式解决极值点偏移问题的过程与功效.

例1已知函数f(x)=ex-ax(a≠0).

(1)讨论f(x)零点的个数;

(2)若f(x)有两个零点x1,x2，且x12.

解(1)当a∈(-∞,0)∪{e}时,f(x)有唯一零点;当a∈(0,e)时,f(x)无零点;当a∈(e,+∞)时，f(x)有两个零点.(过程略)

(2)解法1常规解法

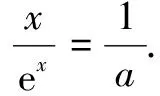
解法2对数平均不等式法

反思比较可见对数平均不等式带来的证明更为简洁、对称、美观. 看似保留双变量，实则通过齐次性隐匿了单变量的身份，这便是该解法的精髓所在.值得一提的是，在高考中对数平均不等式需要证明，此处不再赘述.

三、不识庐山真面目,只缘身在此山中

必须承认,直接应用对数平均不等式远不能解决所有双变量对称齐次形式的问题.因此，需要我们将对数平均不等式进行变式推广.

例2已知函数f(x)=ex-ax2-ax.

解(1)略.

(2)f′(x)=ex-2ax-a，由f′(x1)=f′(x2)=0，得

②

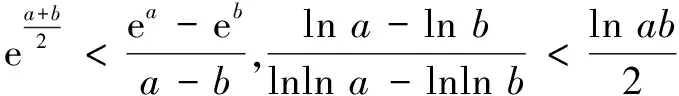
四、山重水复疑无路,柳暗花明又一村

在处理完双变量齐次对称式后，我们不禁疑惑，对于双变量非对称齐次式又该如何解决呢?事实上，纵使对数平均不等式在此处已无用武之地，但其相除、相减的思想是深刻而普遍适用的.下面的例题将展示这种熟悉而惊艳的数学方法，这也是对数平均不等式留给我们的瑰宝.

(1)略;

解(2)由h′(x)=lnx-ax，依题意得lnx1=ax1,lnx2=ax2，于是有

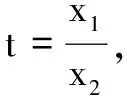
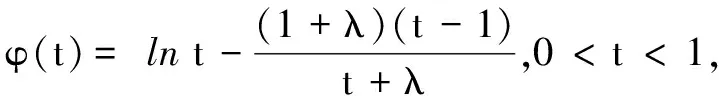
若λ≥1，则φ′(t)>0,φ(t)在(0,1)单调增，得φ(t)<φ(1)=0，符合题意.

若0<λ<1，则当t∈(0,λ2)时，φ′(t)>0,φ(t)单调增;当t∈(λ2,1)时，φ′(t)<0,φ(t)单调减.又φ(1)=0，故φ(t)在(0,1)内不能恒小于0，不合题意.

综上，λ≥1.

授人以鱼不如授人以渔.通过以上探究我们可以发现,在数学学习中不能以背结论的方式解题，而应深刻挖掘每个结论背后所蕴含的数学思想与方法，通过一例掌握一类题，数学能力才能得到快速提高，数学思想的领悟才会变得更深刻.

(指导老师：吴昊)