基于支持向量机算法的岩浆硫化物矿床硫元素预测模型

李猛猛，刘敬党，梁天意，谭 亮，王 刚，朱 玺

1.辽宁工程技术大学矿业学院，辽宁 阜新 123000 2.辽宁省化工地质勘查院有限责任公司，辽宁 锦州 121000 3.中煤科工集团沈阳设计研究院有限公司，沈阳 110015

0 引言

关于岩浆硫化物矿床的研究始于1886年加拿大Sudbury矿床的发现，近半个多世纪以来，中国的金川、加拿大的Voisey’s Bay、澳大利亚的Agnew等矿床的发现进一步将岩浆硫化物矿床的研究达到了空前的火热程度[1]。

岩浆硫化物矿床的形成大多数源于幔源岩浆与地壳的相互作用[2]，硅酸盐岩浆的混入导致早期的硫化物不混溶[3]。岩浆硫化物矿床中的硫化物熔体可以描述为Fe/(Fe+Ni+Cu)显著小于1的FeS-NiS-CuS溶液[4]，是由镁铁质或超镁铁质岩浆中硫化物的分离和聚集以及硅酸盐岩浆中铜元素的分离形成的。主要可分为两大类：一类以富硫化物质量分数>10%的镍和铜为主，另一类以硫化物质量分数<5%的PGE为主[3]。

岩浆硫化物矿床的成矿模型普遍认为主要有两种：岩浆通道堆积模型；深部熔离-多次贯入模型[5]。Naldrett[6]提出了阶段式岩浆镍铜硫化物矿床的成矿模型，主要包括：源岩浆的诞生(地幔熔融)；岩浆的发育(上升到地壳)；岩浆的富化(与地壳的相互作用和早期不混溶硫化物的形成)；岩浆的输送(不混溶硫化物岩浆上升至地壳顶层)；硫化物的生长(岩浆侵位过程中硫化物质量分数的变化)；岩浆对硫化物的滋养(进一步流动的岩浆使硫化物更富集)；完全成熟(岩浆和相关硫化物的冷却和结晶)。建立的岩浆硫化物矿床成矿模型，突显了硫化物的饱和程度和各元素之间亲和性对于研究成矿规律的重要性。Yuan等[7]对塔里木地区玄武岩中的镍、铜和PGE进行了研究，并指出玄武岩中的(Cu/Zr)PM、(Pd/Zr)PM、(Pd/Cu)PM比率极低，从而证明玄武岩中的亲铜、亲硫元素极度耗竭，侧面反映出岩浆在不混溶阶段，硫饱和岩浆吸收了大量的镍、铜等亲铁、亲硫、亲铜元素，这也验证了该地区的岩浆体系在硫饱和前经历了硅酸盐分馏过程。Barenan等[8]的研究表明异常高的Ni/Cu高镍富集硫化物在自然界中十分普遍，橄榄石中也富含镍，硫化物与含橄榄石硅酸盐岩浆之间的平衡源于铁和镍的置换，并用交换系数说明形成它们的各元素之间呈非线性关系。Peter等[9]强调硫化物质量分数的变化与侵入岩的演化有关，对于硫化物岩浆的运移规律、状态研究是分析该类矿床分布规律研究的突破口。前人对于岩浆硫化物矿床成矿模型的建立多是在主量元素、微量元素和同位素数据的基础上进行相关图件的理论分析，根据所处的构造环境进行成矿规律的总结。而在成矿过程中各元素之间所表现的非线性关系多以简单的数学公式进行研究。地质成矿过程作为非线性科学和复杂性理论的代表，在科学快速发展的今天，多学科的相互结合已成为探寻成矿规律的主要手段。

支持向量机(SVM)是20世纪70年代根据统计学习理论提出的一种监督的非参数统计学习方法，有着严格的理论和数学基础，是一种针对小样本情况下新的机器学习方法。SVM不同于传统的基于经验风险最小化原则的学习方法，它是基于结构风险最小化的原则，在解决小样本、非线性及高维问题时表现出很多独特的优势，例如在生物学[10]、医学[11]、生物信息学[12]、模式识别[13]、图像分类[14]和金融[15]等领域应用十分广泛。

本文通过运用SVM算法，基于加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床钻探工程的样品分析数据，综合研究镍、铜元素与硫元素之间的关系，建立以硫元素质量分数为主导的岩浆硫化物矿床的成矿预测模型，并以此作为突破口，探寻岩浆镍铜硫化物矿床的成矿规律。

1 地质背景

加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床于1994年被发现，到目前为止，已开采、查明和推测的矿石储量为1亿t，品位为镍1.94%、铜1%、钴0.11%，是世界上第六大岩浆硫化物矿床聚集地。矿床主要位于Nain省与Churchill省之间Torngat造山带的接触部位，属于裂谷或大陆边缘裂谷环境。矿床的形成主要与沿此部位侵入Nain中元古代镁铁质火成岩系的Voisey’s Bay侵入岩(VBI)有关。Voisey’s Bay侵入岩是Nain深成岩系的一部分，以45°倾向发育于年龄为1.86～1.74 Ga的Tasiuyak片麻岩缝合线东西向延伸的构造区域内，Nain深成岩系由花岗岩质、斜长质、长英质、橄长岩和辉长岩侵入体组成，形成时代为1.34～1.33 Ga[9]。

VBI由一系列花岗岩、斜长岩、橄长岩、橄榄辉长岩及多变橄长岩等组成，形成时代为1.33 Ga。从东到西，由Eastern Deeps、Southeast Extension、Ovoid、Discovery Hill(棕色Enderbitic片麻岩区域)和Reid Brook(黄色Tasiuyak片麻岩区域)等矿区、矿床组成(图1)。矿化由块状、半块状、角砾状和浸染状磁黄铁矿、镍黄铁矿和黄铜矿组成，主要位于靠近岩脉的片麻岩内。半块状硫化物中含有副片麻岩、富铁辉长岩厘米级到米级新鲜-蚀变的镁铁质-超镁铁质岩包裹体，以近水平构造的无矿细粒橄榄辉长岩和强烈挤压角砾岩系列为标志。浸染状硫化物中含有0.50～5.00 cm的副片麻岩包裹体，但不含富铁辉长岩或镁铁质-超镁铁质包裹体。围岩蚀变表现为弱-中等矿化的结构多变橄长岩晕，标志层以硅质矿物、包裹体岩组和硫化物所显示的构造为主。矿体的原生岩浆为高镁玄武质，含有极低的铂族元素和金元素。对矿石的微量元素和铅、钕同位素地球化学分析表明，矿床的形成源于地幔与地壳岩石的相互作用，发育在深部和侵入岩的接触带附近。硫、氧同位素研究表明矿床的形成与局部片麻岩有一定的相互作用。Voisey’Bay镍铜硫化物矿床的形成来源于它所处的管道系统，该系统中经历了多次的岩浆脉冲[6,16]。

关于Voisey’s Bay镍铜硫化物矿床的成因，Peter 等[9]提出Nain火成岩系镁铁质岩浆作为硫饱和熔体离开地幔，受到不同程度的地壳物质混染，硫化物主要在深部熔离，然后以“晶粥”形式贯入成矿。Chusi 等[17]提出Tasiuyak片麻岩的作用是十分重要的，为岩浆提供了足够的硫元素并促使硫化物饱和，而且认为岩浆曾遭受围岩多次的混染，早期是中下地壳太古宙岩石的混染，晚期是在上地壳遭受古元古代Tasiuyak片麻岩的混染。通过对混染作用的研究，认为周围捕虏体对岩浆的影响可能是深入认识岩浆镍铜硫化物矿床形成的重要途径。虽然近些年对岩浆硫化物矿床的成因有着诸多的研究，但统一认为受到岩浆混合作用的影响是形成岩浆硫化物矿床的关键因素。

2 数据来源

通过对加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床资料的综合研究，选取穿过Eastern Deeps岩体中部与边缘的VB95-266和VB96-254两个钻孔33个样品数据进行试验，钻孔深度小于1 km，钻孔位置见图1，样品数据见表1。

所有的样品使用鄂式碎石机破碎至-10目，而后使用碳化钨环磨至-150目。样品采用四酸过程进行分解，测试仪器是Perkin-Elmer电感耦合等离子仪，进行镍、铜元素质量分数的测定，测定限均为0.02×10-6。硫元素质量分数的测定用的是Leco燃烧法，测定限为0.20×10-6。

据文献[9]修编。

图1 Voisey’s Bay矿床地质简图

Fig1 Geological sketch of Voisey’s Bay mining deposits

3 SVM预测模型

3.1 方法原理

SVM算法是一种广泛应用于分类及回归问题的机器学习方法，该算法是基于统计学理论、Vapnik-Chervonenkis dimension(VC维)理论和结构风险最小化原理的基础上建立而成的，依据有限样本信息在模型中的复杂性和学习能力之间探寻最佳方案，以获得最好的泛化性能[14]。针对非线性不可分问题，则通过核函数将数据由低维空间映射到高维空间，进而实现高维可分[18]。

SVM的基础是寻找在线性可分条件下的最优分离超平面，首先给定一个样本集S= {(xi,yi);i= 1,2，…,n,xi∈Rd,yi∈ {+1, -1}}，其中，xi为数据，yi为数据所属的类别。SVM的原始问题可表示为：

yi(ωxi+b)≥1-ξi;

(1)

式中：ω为权重向量；b为偏置向量；ξi为松弛因子；C为惩罚因子[19]，可通过调节该参数实现算法复杂度与分类精度的平衡。通过求Lagrange函数的极值点得到原始问题的最优解。引用Lagrange乘子算法，将上述原始问题转化为对偶形式[20]，表示为：

(2)

式中：Q(α)为最终需要计算出的决策函数；α为Lagrange乘子；αi和αj为α最终确定前的变量值；通过调节αi,αj和C的取值，最终实现算法复杂度与分类精度的平衡。

对于非线性不可分样本，SVM通过非线性映射将样本(xi,xj)映射到核函数K(xi,xj)指引的高维特征空间中，在特征空间中实现内积运算[21]；故在非线性不可分情况下，公式(2)可表示为：

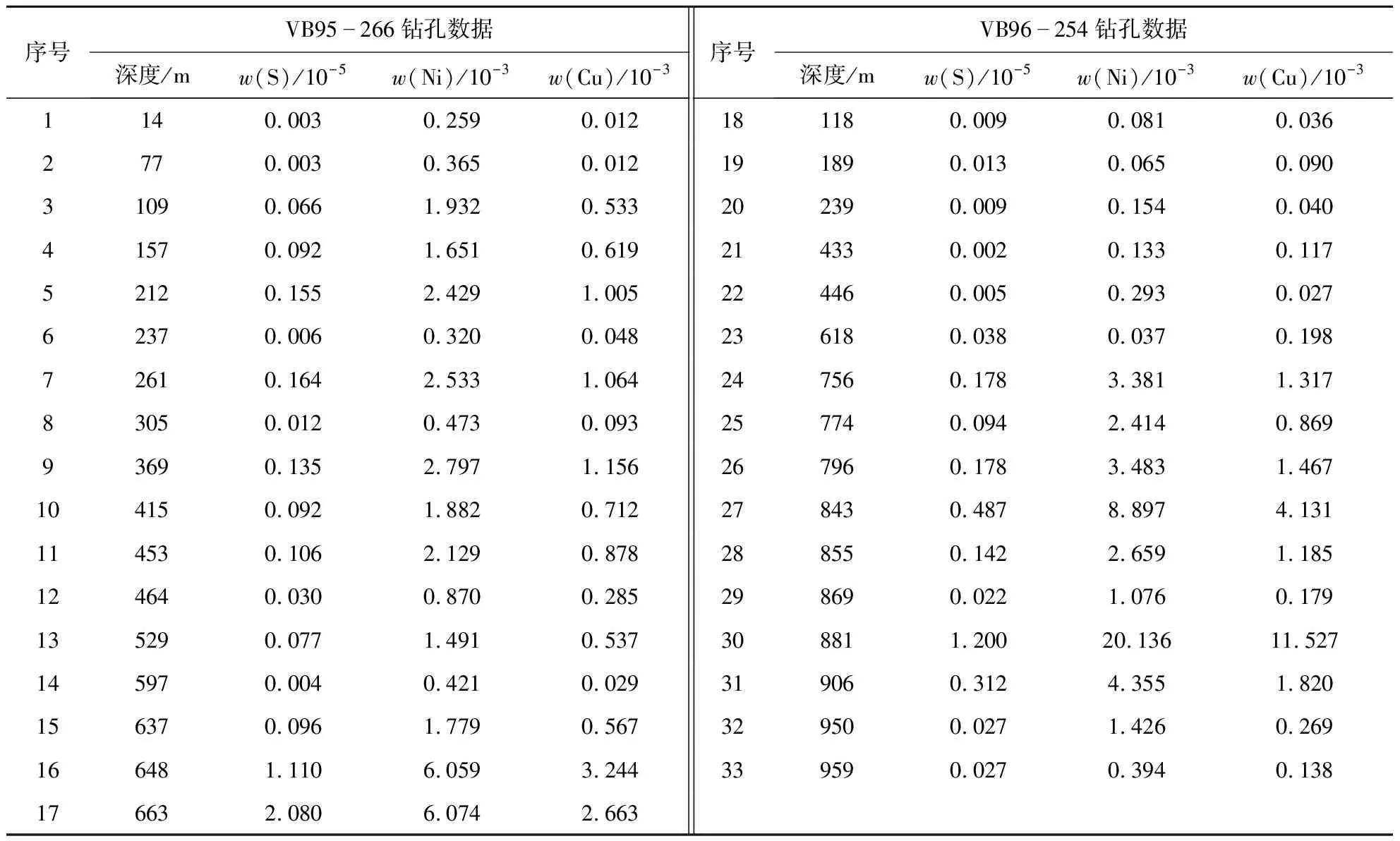
表1 岩心样品分析数据

(3)

常用的核函数K(xi,xj)有多项式核函数、径向基核函数(RBF)及Sigmoid核函数等。对于核函数的选择，样本数据在进行回归估计时都有相应效果最好的核，但在缺少先验知识过程时，多项式核函数无法进行前期的正交化过程，而且该样本数据不满足Sigmoid核函数的半正定条件。RBF主要是分析训练样本距原点距离的实值函数[14]，故本文选择RBF作为SVM分析的核函数，其数学表达式为

(4)

式中：σ为置信范围；γ为间隔。

3.2 预测模型

3.2.1 基本分析

对样品数据进行散点图分析(图2)。图2a中由于标度较大，镍、铜元素质量分数整体上随硫元素质量分数增加呈线性增加；图2b中由于标度较小，数据表现为局部集中，局部集中数据呈非线性状态。

3.2.2 SVM分析

将VB95-266和VB96-254钻孔数据以样本集的形式，通过Matlab软件应用SVM算法进行数值模拟，以镍、铜元素质量分数作为输入值(自变量)，以硫元素质量分数(因变量)作为输出值进行拟合实验(图3)，其中C=1×104，γ=1，探索它们之间的近似解析函数关系和曲线方程，步骤如下：

1)将VB95-266和VB96-254钻孔数据代入公式(1)，以镍、铜元素质量分数作为输入值(自变量x)，以硫元素质量分数(因变量y)作为输出值，将数据转变为样本集的形式。

2)将样本集代入公式(2)，对样本集进行线性、非线性判别。经判别，样本集整体及局部均呈非线性关系。

3)将样本集代入公式(4)，由非线性原样本集转变为线性样本集。

4)将经过RBF转变为线性的样本集代入公式(3)，以硫元素质量分数作为原值，以镍、铜元素质量

a. 将本次研究的所有样本进行投点分析；b. 硫元素质量分数在(0.00～2.00)×10-6区间集中分布的放大图。

图3 SVM网络结构图

分数经SVM计算出的值作为预测值，进行拟合分析。

首先对全部样本集进行SVM拟合分析。全部样本集样品数量为33个，样品位置区间为14～906 m，方差大于9.712×10-7。根据预测值和硫元素原值的偏差曲线(图4)可以看出，所有样本进行统一拟合效果很差，说明镍、铜元素质量分数与硫元素质量分数整体上不具备一定的规律性。

其次根据图2b和结合图2a中>2.00×10-6所示的4 个样本富集区间分别进行拟合测试。硫元素质量分数区间分别为：3.12×10-6～20.80×10-6、1.35×10-6～1.78×10-6、6.60×10-7～10.60×10-7、2.00×10-8～38.00×10-8。之后将4个样本富集区间数据进行合并，再一次进行拟合测试，剔除拟合效果差的试验，将硫元素质量分数区间1.35×10-6～1.78×10-6和6.60×10-7～10.60×10-7合并为6.60×10-7～17.80×10-7(两组样本之间数据空白的区间可能受到样本数量的影响)。最终将拟合效果好的拟合测试结果主要划分为3个阶段，

图4 全部样本集偏差曲线拟合图

以样品位置由深到浅的顺序分别进行描述与分析。

1)硫元素质量分数区间为3.12×10-6～20.80×10-6，样品数量为5个，样品位置区间为648～906 m，方差小于1.44×10-7，预测值和硫元素原值的偏差曲线拟合效果很好(图5a)。该区间硫元素质量分数起伏较大。

2)硫元素质量分数区间为6.60×10-7～17.80×10-7，样本数量为13个，样品位置区间为109～885 m，方差小于1.37×10-9，预测值和硫元素原值的偏差曲线拟合效果很好(图5b)。该区间硫元素

a. 样本区间为3.12×10-6～20.80×10-6；b. 样本区间为6.60×10-7～17.80×10-7；c. 样本区间为2.00×10-8～38.00×10-8。

质量分数起伏较平稳。

3)硫元素质量分数区间为2.00×10-8～38.00×10-8，样品数量为15个，样品位置区间为14～959 m，方差小于1.56×10-10，预测值和硫元素原值的偏差曲线拟合效果很好(图5c)。该区间硫元素质量分数起伏较大。

3.2.3 模型验证

选取VB95-266和VB96-254两个钻孔未进行SVM分析的12个样品数据进行模型验证，钻孔深度小于1 km，样品数据见表2。

以镍、铜元素质量分数作为输入值，经过SVM分析计算硫元素质量分数的计算值(输出值)，通过与硫元素原值对比，误差小于0.71×10-10(表3)。

通过以上对于模型的验证分析，证明该模型效果较好。

4 讨论

基于SVM镍、铜元素质量分数与硫元素质量分数的基本分析和SVM分析，可以看出镍、铜元素在成矿过程中与硫元素之间整体上呈现出无规则的混沌状态，通过分区间的SVM拟合分析，其中的关联又呈现出一定的非线性关系。由于在矿产勘查中样本集只是在探索成矿规律中的小样本事件，无法准确掌握每一个成矿阶段的界限，学者们将分形和混沌理论引用到成矿规律的研究中，借以探索成矿过程中的非线性关系。

为了说明镍、铜元素与硫元素在各成矿阶段时间序列上的复杂性及所处的运动状态，同时也为了验证基于SVM算法建立成矿预测模型的可靠性，本文通过引入分维值和李雅普诺夫指数的相关计算，作为SVM算法准确性的定量评价。

4.1 方法原理

分数维是度量事物复杂性最主要的指标。对于成矿阶段复杂性的研究，本文采用分数维进行相关刻画。由于镍、铜、硫元素质量分数之间无法用尺度来测量，传统的尺码法、小岛法、计盒维数法不适用于文章中分维值的计算，故本文用计算时间序列分维值的G-P法进行分维值的计算[22]。

根据Takens的嵌入相空间原理[23]，硫元素质量分数作为镍、铜元素富集成矿的重要因素，故将各阶段硫元素质量分数值进行相空间重建，将质量分数区间值x1,x2,x3,x4,…重新排列成m维相空间X(t)：

表2 岩心样品验证数据

表3 样品数据数值误差表

X(t)={x(t),x(t+τ),…,x(t+iτ)} 。

(5)

式中：τ为延迟时间；t=0,1,2,…，n。

建立相空间后，我们任给一个小尺寸r，然后设N为(xi,xj)之间距离小于r的数据点数，则相关积分的定义为

(6)

式中：θ(x)为Heaviside函数，当x<0时，θ(x)=0，当x>0时，θ(x)=1，当x=0时所求为自身，无意义。C(r)为标准相关函数，对于较小的r，C(r)表现为r的幂，C(r)∝rD。则分维值为

(7)

李雅普诺夫指数是用来判定一个系统混沌性的，故本文采用李雅普诺夫指数的计算来判别每个成矿阶段的运动状态[24]。

镍、铜元素质量分数对于硫元素质量分数变化(初始条件)的敏感性，是系统运动状态出现混沌的关键特性。将硫元素质量分数代入离散映射描述的系统xn+1=f(xn)，若初始值x1和x2相差d0=x1-x2,经过n次迭代后：

(8)

式中，λ为李雅普诺夫指数。则

(9)

式中：λ<0，体积收缩，运动呈稳定状态；λ=0，运动呈稳定状态；λ>0，运动呈混沌状态。

4.2 阶段划分

4.2.1 硫饱和阶段

SVM预测模型中，在硫元素质量分数区间为3.12×10-6～20.80×10-6的图5a中，不同样品硫元素质量分数差别较大，质量分数较高，偏差曲线起伏明显，主要分布在600 m以下的样品中。根据公式(5)(6)和(7)计算的D=0.35，根据公式(8)和(9)计算的λ>0，处于混沌状态。推测该阶段为硫化物岩浆脱离主岩浆室，进而进入上岩浆室后残留的原始状态。

岩浆硫化物矿床的形成可能受到岩石圈和地幔的交代作用[25]，早期的镁铁质岩浆与硅酸盐岩浆的混合，是岩浆硫化物矿床形成的根本原因[26-27]。

在镁铁质岩浆方面，在富水富硫的岩浆演化初期，橄榄石、斜辉石及尖晶石等开始结晶，呈悬浮状态存在于岩浆中，并随黏度的增加而增加。硫化物岩浆很少能被留存在岩石中，偶在古老火山岩中见到硫化物呈滴液状分布在橄榄石中[28]。镁铁质岩浆中以亲铁性为主逐渐转变为亲硫性，大量吸收铁元素形成硫化铁(磁黄铁矿)，并在岩浆室多处小范围汇聚。在亲铁性作用下，吸收硫、铜、镍元素的岩浆开始活跃；在亲硫性作用下，镍和铜元素在岩浆中开始扩散平衡，最终大量存在于硫化物汇聚的位置；与此同时,在温度、压力的作用下金属元素与硫化物发生置换反应，液态镍黄铁矿、黄铜矿等相继产生，导致镍和铜元素质量分数达到富集，并分布不均，形成富集金属的硫化物岩浆[29]。

在硅酸盐岩浆方面，硅酸盐岩浆中亲铜元素(硫、金等)、亲铁元素(铜、镍、硫、钌、铑等)及亲硫元素(铂、钯等)开始分解为以硫化物为主(图6)，促使在与铁镁质岩浆混合后小面积聚集的硫化物熔体中富含大量的金属元素。对于该方面的分析，从橄榄石的滴液硫化物中发现硅酸盐包裹体可以证明[30-31]。

Ariskin等应用COMAGMAT-5模型分析了在橄榄石结晶累积过程中观察到温度最高为1 289 ℃(Ol+硫化物)，岩浆达到平衡时温度为1 185 ℃(Ol+Opx+硫化物)，最终得到最低温度为1 116 ℃(Pl+Pig+硫化物)，其他矿物相应质量分数见表4[32]。从中也可以说明，岩浆经过混合-平衡阶段温度及组分的变化。

图6 元素亲和性简图

表4 硫化物岩浆平衡时矿物相温度及其他矿物质量分数

加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床中存在很多现象，包括在Oviod矿区中存在一个方黄铜矿富集的区域，铑、铱、锇和钌含量变化均为由外向内增高、磁铁矿粒度差别大，为2～100 cm不等。受到亲和性的作用，铂族金属在矿床中含量分布不均等[33-34]，均是受到镁铁质岩浆与硅酸岩岩浆混合后平衡程度的影响。矿床中铂族元素和金元素的含量低，可能是残留在地幔中的硅酸盐岩浆的硫化物[35]。

4.2.2 硫成矿阶段

SVM预测模型中，在硫元素质量分数区间为6.60×10-7～17.80×10-7的图5b中，不同样品硫元素质量分数差别近乎平稳，偏差曲线呈上凸状态，预测值和硫元素原值的偏差曲线拟合效果很好。该区间样品位于100～900 m不等，除了顶层和底层，分布于钻孔的各个位置。根据公式(5)(6)和(7)计算的D=0.60，根据公式(8)和(9)计算的λ>0，处于混沌状态。推测硫化物岩浆受到温度、压力及围岩侵入等外来因素的影响，在不同的成矿空间时刻改变着硫、镍和铜等元素的质量分数。

受到构造运动的影响，提供了岩浆硫化物矿床的成矿空间。压力迅速减小，围岩(Tasiuyak片麻岩)大量侵入硫化物岩浆[36]，伴随着水和气体的入侵，本已达到平衡的岩浆状态再一次受到侵扰，亲铁性、亲硫性和亲铜性受到限制，铁、硫、铜元素等再次活跃起来，在亲氧性和亲气性元素的参与下再一次达到平衡[37]。

Voisey’s Bay镍铜硫化物矿床硫化物的Se/S值与Tasiuyak片麻岩的全岩样品基本相同，δ13C值相差-24.8%～-18.3%[38]，说明随着时间的积累和干扰因素的增加，在岩浆通道内岩浆的成分发生着快速的变化，在岩浆通道内形成富含金属的硫化物分布不均，呈逐渐减少的趋势，铁、硫和铜元素等会被小周期元素置换(也可能受到催化剂的催化作用)，高碱金属元素质量分数的增加，促使三价铁趋于稳定[39-41]。在高碱金属元素质量分数、水质量分数、氧逸度增加的同时，硫化物饱和硫质量分数也会相应的增加，并达到峰值，但在硫化物岩浆中的增加是有限的[42-43]。经过以上过程促使硫化物岩浆再一次达到平衡，形成岩浆位置由深到浅，硫、铜、镍元素质量分数由多到少的成矿阶段。

4.2.3 硫流失阶段

SVM预测模型中，在硫元素质量分数区间为2.00×10-8～38.00×10-8的图5c中，可以看出不同样品硫元素质量分数区间差别较大，偏差曲线起伏明显，样品位置深度多在400 m以上，根据公式(5)(6)和(7)计算的D=0.94，根据公式(8)和(9)计算的λ=0，处于稳定状态。推测是岩浆硫化物矿床成矿后经过几十亿年的地表作用(空气、水等)和矿石内部的变质作用下，硫、镍、铜元素进一步流失，被带入地表土中，这也说明应用化探方法对于探矿所起到的关键作用。

硫化物岩浆成矿后，矿体在空气和水的侵蚀下，水的扩散成为了硫化物流失的重要载体[44-45]。矿体遭受风化淋滤作用开始氧化，主要受到下几个方面影响：1)角砾岩系列的存在提供了空气和水在矿体中的空间；2)原生硫化物的氧化(黄铜矿、磁铁矿和硫铁矿等)；3)pH值的降低；4)高可溶性次生矿物吸收了大量金属元素等条件促使硫、镍、铜元素流失[46]。

5 结论

1)基于SVM方法对加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床中的2个钻孔数据进行拟合试验，对镍、铜元素质量分数与硫元素质量分数进行相关性分析，建立了基于硫元素质量分数区间的预测模型。根据预测模型计算的结果，将岩浆硫化物矿床的成矿过程划分为3个阶段，分别为硫饱和阶段、硫成矿阶段和硫流失阶段。通过与前人的理论研究进行对比，揭示了该模型的可靠性。

2)根据预测模型计算结果划分的3个阶段，证明了加拿大拉布拉多Voisey’s Bay镍铜硫化物矿床在经过硅酸盐和硫化物岩浆不混溶的阶段后，很可能还存在于岩浆管道周边和底部的浅盆地区，以及其他镁铁质基岩中存在硫富集的地段。同时侧面验证了钻孔地区周边矿床的存在，为下一步找矿工作提供了相关依据。

3)基于SVM方法关于岩浆硫化物矿床建立的预测模型应用性很广，以镍和铜元素质量分数可以计算出硫元素质量分数的大致区间，特别在找矿过程中，样品多为地表或地表浅层样品，硫元素质量分数的测试结果多受到地表因素的影响而缺乏可靠性。根据SVM预测模型计算出硫元素质量分数预测值所在的质量分数区间，可推测出矿床的形成阶段，加深岩浆硫化物矿床的研究，指导隐伏矿床的发现。

致谢：文章建模部分得到了桂林理工大学王玉老师的认真修改，在此表示感谢。