基于双电层模型的频域震电响应数值模拟

韩 丽, 胥铁潇, 金胜昔, 董文宇, 嵇艳鞠

吉林大学仪器科学与电气工程学院，长春 130026

0 引言

地震的孕育和发生过程中常常会出现电磁异常扰动。研究认为地震波到达之前产生的电磁信号是与震源相关的，而与地震波同时到达的电磁信号则与当地的场地条件相关[1-2]。但目前对这些地震电磁信号产生的机制仍存有争议。

许多学者推测双电层动电效应是最有可能的机制之一，这是因为动电效应要求介质是孔隙介质，是普遍存在于地壳表层地层中的[3-7]。动电效应与孔隙流体的运动是密切相关的，通过地震孕育和发生过程中的动电效应研究，进一步了解地震中引发电磁异常现象的机制，对于地震预报和监测、防震减灾都有重要意义[8-9]。

传统的震电响应建模中，电磁部分以确定的地震场为源，采用准静态近似的方式，通过求解电势的泊松方程获得电场[10-17]。这种准静态近似的方式可以降低模拟难度，能一定程度提高计算效率；然而准静态近似在震电响应模拟中会带来数值误差，尤其是在高矿化度条件下，误差特别显著[4]。并且这种方法必须满足准静态近似条件，即模型区域必须在静电近场范围内，频率也位于一个较低的区间范围。

本文基于Maxwell全方程的频域有限差分方法，进行了震电响应的频率电磁响应数值模拟，并分析和讨论在均匀弹性介质中，电导率层状和电导率异常体模型下的震电特征，其中模型均没考虑自由地表影响。

1 基于Maxwell全方程的频域震电响应模拟

有限差分方法是采用数值近似的方法，将原本连续的函数离散化，形成线性方程组，之后借助计算机来进行大规模计算的一种方法。

本次借助频域有限差分方法，可以大大简化在复杂空间中进行波场计算的计算量，在二维空间中将空间分割成一个个网格(图1)。

Ex1--Ex6为网格棱边上x方向的电场分量；Hz1--Hz4为网格面上z方向的磁场分量。

图1 二维频域有限差分图

Fig1 Two dimensional FDFD

在计算时每一个网格单独计算，这样在计算复杂空间模型时，不会因复杂的边界条件而大大增加计算成本。地震波造成动电效应产生电磁波频率较低，此时可以忽略位移电流，将Maxwell方程简化成：

×E=-iωμ0H;

(1)

×H=σE;

(2)

·E=0;

(3)

·H=0。

(4)

式中：ω为角频率；E为垂直极化的横波(PSV)和水平极化的磁场(TM)波产生的电场；H为磁场；i为虚数单位。其他参数参见表1。

与单一电磁场频域有限差分不同的是，在动电效应中，产生的电磁波是由地震波在介质中传播所激发的，因此在场中没有电流源，渗流位移代替电流成为了电磁场的初始条件之一。

本次模拟耦合地震波和电磁(EM)波的理论基础是Pride震电耦合控制方程。为简化方程，我们忽略了地震感应电磁场的反馈，在前半部分以格林函数解析的方式来求解地震Biot方程；而对于电磁部分，不同于传统引入准静态近似的方式，我们将采用Maxwell全方程来求解电磁波场。

表1 介质参数、符号、值和SI单位

考虑二维有限域各向同性的流体饱和多孔介质，通过丢弃电过滤反馈，Pride震电耦合控制如下：

(5)

(6)

(7)

(8)

(9)

×E=-μH。

(10)

式中：v为固相粒子速度；q为平均相对流体速度；τ为应力；ρ=(1-φ)ρs+φρf，为体积密度；ρm=Tρf/φ,为有效的流体密度；P为孔隙流体压力；i和j为变量x或者y的方向；以固相粒子速度v为例，vi,j为vi在j方向的空间偏导数，vj,ji为变量vj在j方向和i方向的空间偏导数之和；变量上方·代表该变量对时间的导数；α、λ和M为弹性模量。α、λ和M由下式给出：

α=1-Kb/Ks；

(11)

(12)

(13)

其余波场参数意义及设置如表1所示。

首先使用格林函数方式求解独立的地震波场结果[16]。其中心思想是在三维空间傅里叶时间-拉普拉斯变换域中建立方程，场量的F(x,t)的时间-拉普拉斯变换：

(14)

式中：t为时间；s为拉普拉斯变换参数，可以选择s=iω将其简化为时间傅里叶变换形式。则其三维空间傅里叶变换为

(15)

式中：kn为波数向量k的第n个笛卡尔向量分量；xn为向量x第n个分量的位置坐标。

以往的震电模拟中使用时域有限差分算法求解。时域有限差分相比频域有限差分算法占用内存更少，可以计算大范围区域的电磁场，但是每一次迭代都要对所有网格全部刷新一遍，计算速度较慢。当计算地震波和电磁波耦合的波场时，电磁波和地震波速度上的巨大差异给计算带来了很大困难。在空间域上，为避免差分算法误差的影响，空间波长要依据地震波波长来确定；在时域上，时间步长又需依据电磁波速度来确定，两者巨大的差距会给结果带来很大的误差。因此本文选择频域有限差分方法来进行计算。

由解耦状态下的电磁场得到电磁控制方程如下：

(16)

(17)

只计算xOy平面上的波场情况，可以将对z方向上的求导结果设置为0，将旋度在直角坐标下分解并简化可得：

(18)

(19)

(20)

式中：qx、qy和Ex、Ey分别为x、y方向的电场分量；Hz、Hy分别为z、y方向的磁场分量。之后再对其进行离散，采用中心差分项代替微分项，可以得到：

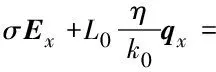
(21)

(22)

(23)

式中，Δx、Δy分别表示在x、y方向的网格步长。

最后对频域差分方程求解，可以解出各个频点的电场值。

2 数值模拟

模型大小均设置为700 m×700 m，网格128×128。此外，源定义在中心网格节点处，接收点定义在网格节点(90, 90)。在水平应力项上加入中心频率为f0= 25 Hz的瑞雷子波作为震源函数，根据格林函数方式[15]计算所得地震渗流速度结果。具体参数设置如表1所示。

在如上设置的全空间模型下，震电响应产生的电场模拟结果如图2所示，可以明显观察出其在全空间模型中的频域波场解。

为了分析复杂介质条件下的震电耦合特性，我们设置一个双层层状介质模型。设置上半层-180～350 m电导率为1×10-2S/m，下半层-350～-180 m电导率为1×10-3S/m(图3)，其他介质参数见表1。由图3可以看出，层状模型和全空间模型中的电场分布不同，可以明显看到电场在分界面的反射和折射现象。

为了模拟现实地质条件的复杂情况，在全空间模型中加入了电导率不同的异常体，大地电导率为1×10-3S/m，异常体电导率为 2 S/m，异常体为设置在x方向140 ～200 m、y方向140 ～200 m处的正方形(图4)，其他介质参数见表1。由图4可以看出，电场在异常体处发生了明显的反常扩散现象，通过图像可以清晰地定位异常体的位置。

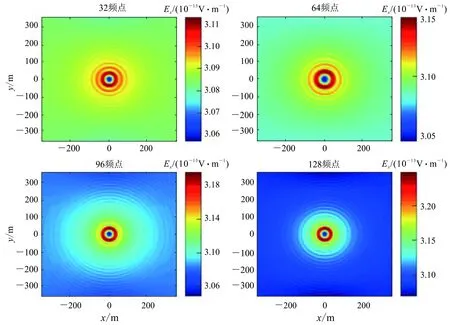
图2 全空间模型的电场频域波场图

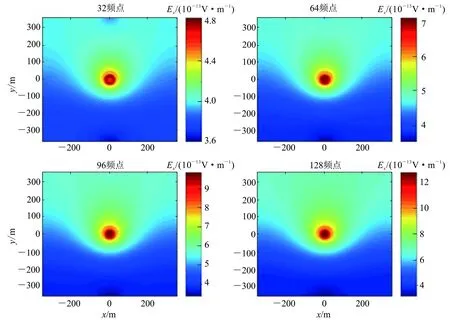
图3 层状模型的电场频域波场图

图4 异常体模型的电场频域波场图

通过层状和异常体的模型与全空间模型的对比，可以看出这种频域有限差分方法可以有效模拟震电响应，并且识别不同介质分界面。

3 结语

本文提出了一种基于Maxwell全方程的频域有限差分方法，模拟分析了以双电层理论为基础的震电耦合效应。在弹性均匀介质中，以电导率双层层状和电导率异常体模型为实验案例，对比全空间模型，分析了震电耦合特性。结果表明本方法能够有效地捕获对比介质界面上地震与电磁波场的反射和透射现象，识别异常位置，突出了地震响应模拟检测地下介质特性的能力。