瞬变电磁法非线性优化反演算法对比
2022-06-22徐正玉付能翼付志红
徐正玉,付能翼,周 洁,付志红
1.重庆大学电气工程学院,重庆 400044 2.科罗拉多矿业学院地球物理系,美国 科罗拉多 80401 3.重庆璀陆探测技术有限公司,重庆 402660
0 引言
瞬变电磁法(transient electromagnetic method,TEM)是利用不接地回线或接地电极向地下发送脉冲电磁场,用接收线圈或电极观测由该脉冲电磁场感应产生的二次场随时间和空间的变化规律来解决有关地质问题的时间域电磁法。目前,该方法已成为浅地表工程地球物理调查的重要方法之一,被广泛应用于工程地质调查、水文地质调查以及环境调查等诸多领域[1-7]。
通过数学物理方法将瞬变电磁二次场信号转换为地层电阻率和深度信息是一个复杂的过程[8-12]。早期地球物理研究人员采用“烟圈”快速成像方法[13-14]。一些线性迭代方法也被用于地球物理数据反演计算中,如高斯-牛顿法、阻尼最小二乘法和自适应正则化反演方法等等[15-19]。上述方法的优点是收敛速度快,计算量较小。与此同时也存在以下不足。例如:“烟圈”快速成像方法近似粗糙,数据处理精度低;在反演过程中,线性迭代方法存在对初始模型依赖性大、反演结果容易陷入局部极小值、灵敏度矩阵计算量大以及对计算机处理器要求高等缺点。
因此,研究人员选择将非线性优化反演算法应用到地球物理反演与成像中并获得成功。1995年,Eberhart等[20]首次提出粒子群优化(PSO)算法,该算法在全局搜索能力和收敛速度方面表现出良好的性能,已被成功用于解决许多领域的问题。Godio、Yuan和Pallero等[21-23]首先将PSO算法应用于电测深数据、大地电磁数据以及其他地球物理方法数据处理。除此之外,其他非线性优化算法也被用于地球物理数据反演。例如:Boschetti等[24]使用遗传算法进行位场数据处理反演;Roy等[25]将蒙特卡罗算法应用于引力场数据和磁场数据反演;Yin等[26]将模拟退火算法应用于航空电磁数据反演。在瞬变电磁数据反演中,Li等[27-28]应用神经网络方法、差分进化算法和PSO算法进行近似一维反演;Xu等[29]将PSO算法应用于TEM数据反演,研究结果表明该算法具有高效的优点。但上述研究内容未考虑随机噪声对PSO算法精度的影响。
2008年,英国剑桥学者Yang[30]提出一种新的智能算法,即萤火虫算法。该算法是一种功能强大的跨学科智能随机算法,已成功应用于许多领域。算法的核心思想来源于萤火虫利用发光的生物学特性进行觅食和求偶的行为。萤火虫算法被提出后,受到众多研究者的关注和研究,并不断得到完善。Abdullah[31]提出一种混合进化萤火虫算法;郝晓莹[32]提出一种自适应步长的萤火虫算法;陈文平[33]提出一种多策略分层学习的萤火虫算法。研究表明萤火虫算法具有良好的搜索能力和优化能力,易于实现,实用性强,参数少,过程简单,被广泛应用于工程和金融等领域。而在地球物理反演与成像中,萤火虫算法的发展非常缓慢。当前,只有Zhou等[34]将萤火虫算法应用到瑞利波数据处理中;王鹏飞[35]将该算法应用于大地电磁数据处理中。
综上所述,PSO算法提出时间早,在地球物理反演中已经发展成熟;而萤火虫算法是近些年来提出的一种新方法,在地球物理资料反演中应用较少。因此,为了比较这两种非线性优化算法的应用效果,本文将PSO算法和萤火虫算法应用于TEM数据反演中。先详细阐述PSO算法和萤火虫算法的原理和求解流程,然后分析了随机噪声对两种算法精度的影响并结合野外瞬变电磁实测数据进行处理,以对比说明两种算法的实际应用效果。
1 非线性反演方法
1.1 粒子群优化算法
PSO算法的核心思想是:将鸟或鱼简化为粒子,粒子的位置代表最优化问题中的可能解,食物的位置代表最优解,所有粒子在一定的规则下,向着最优解位置运动[20]。
在寻优开始时,粒子群优化算法首先在搜索区域范围内随机初始化m个粒子,作为迭代初始值,然后实时更新自己的速度及位置:
(1)
(2)

PSO算法的求解过程(图1)如下:
1)PSO算法参数设置。设定粒子数目和最大迭代次数,确定c1、c2、ω的取值。随机产生每个粒子的初始位置、初始速度以及速度迭代变化的取值范围。

图1 PSO算法计算流程图
2)根据目标函数计算每个粒子的适应度,并根据适应度更新每个粒子的个体最优位置和群体最优位置。算法迭代计算第一次时,个体最优位置就是初始位置,群体最优位置是适应度最好的粒子位置,当最优位置适应度优于迭代前时,更新最优位置,否则保留原位置。
3)判断误差精度或达到最大迭代次数。判断计算结果是否达到误差精度要求或达到最大迭代次数。如否,进行下次迭代,更新粒子速度和位置,并计算新的适应度,再进行步骤2),直到满足终止条件停止迭代,输出结果并保存。
1.2 萤火虫算法
萤火虫算法是模拟自然界中萤火虫发光的生物学特征发展而来的,是基于群体搜索的随机优化算法[8]。标准萤火虫算法的核心思想是,每个萤火虫的位置代表待求解问题的一个解,萤火虫的发光亮度代表待求解问题的目标函数值,目标函数值越好,亮度越强。亮度弱的萤火虫被亮度强的萤火虫吸引,并向其移动。随着迭代的进行,种群中亮度弱的萤火虫不断向比自己更亮的萤火虫移动,最终大多数萤火虫会聚集在最亮的萤火虫附近,最亮的萤火虫的位置就是问题的最优解。
如上所述,萤火虫算法有两个因素,即亮度和吸引度。定义萤火虫的相对亮度为
I=I0·e-γrij。
(3)
式中:I0为萤火虫绝对亮度,与目标函数相关,目标函数越优绝对亮度越大;γ为光吸收系数;rij为萤火虫i和j之间的距离。rij计算公式为
(4)
式中:xi和xj分别为萤火虫i和j在空间中的位置;d为模型参数的数目。萤火虫的吸引度为
(5)
式中:βij为萤火虫i和j之间的吸引度;β0为最大吸引力,通常取1。当微弱的萤火虫移动到最亮的萤火虫时,其位置更新为
(6)
式中:α为步长因子;R为[0, 1]内的随机数;ε为在参数范围内随机生成的位置矢量。
萤火虫算法的求解过程[35](图2)如下:
1)萤火虫算法参数设置。设置萤火虫数目m、β0、γ、α,以及最大迭代次数或搜索精度。
2)随机初始化萤火虫位置,计算目标函数,并将其倒数作为各自绝对亮度。
3)计算群体中萤火虫的相对亮度和吸引度,根据相对亮度决定萤火虫的移动方向。
4)更新萤火虫的空间位置,根据更新后的萤火虫位置重新计算萤火虫的亮度。
5)当满足误差精度或达到最大迭代次数时转到下一步;否则增加迭代次数,转到步骤3)进行下一次迭代搜索。
6)输出全局极值和最优个体解,保存结果。

图2 萤火虫算法计算流程图
2 适应度目标函数构造
通过汉克尔变换和正、余弦变换或G-S逆拉普拉斯变换可以求解水平层状介质磁场强度垂直分量正演响应[29]。构造适应度目标函数为
(7)
式中:N为时间道数目;hcn和hsn为第n个时间道垂直磁场正演计算响应和实测数据响应。定义误差为目标函数,求解最优解就是求目标函数f为最小时的电阻率值。目标函数越小即误差越小,表明正演计算响应与实测数据响应越接近。
3 理论数据处理
3.1 无噪声理论数据反演
首先,选择无噪声理论数据测试PSO算法和萤火虫算法的性能。建立三层和四层理论地电模型。三层地电模型第一、二、三层电阻率(ρ1、ρ2、ρ3)分别为20、100、20 Ω·m,厚度(h1、h2、h3)分别为50、100 m和无限大;四层地电模型第一、二、三、四层电阻率(ρ1、ρ2、ρ3、ρ4)分别为100、20、100、50 Ω·m,厚度(h1、h2、h3、h4)分别为50、100、100 m和无限大。利用余弦变换和汉克尔变换进行三层和四层理论地电模型的正演计算[29],然后采用PSO算法和萤火虫算法对其进行处理。此外,还选择“烟圈”快速成像方法进行比较分析。在PSO算法中,c1=c2=2,ω=0.99k·r3/2+0.1(r3为[0, 1]内的随机数),m=50;在萤火虫算法中,α=0.1,γ=0.8,m=50。两种算法均迭代计算60次。
图3为三层地电模型的反演结果。从图3a可以看出,第二层高阻体的“烟圈”快速成像方法反演结果与理论模型相比误差较大;而PSO算法和萤火虫算法的反演结果与理论模型一致。从图3b可以看出,在前5次迭代中,PSO算法的误差远大于萤火虫算法的误差;但随着迭代计算进行,两种算法的误差均收敛于稳定值且萤火虫算法误差一直小于PSO算法。
图4为四层地电模型的反演结果。从图4a中可以看出,“烟圈”快速成像方法反演结果与理论模型相比具有较大误差,并且只有第一层和第二层的电阻率信息得到客观反映,第三层和第四层效果不明显,深度信息误差大且精度低;而PSO算法和萤火虫算法能较好地反映出理论模型的电阻率和深度信息,但是在电阻率较高的第三层中,两种算法获得的电阻率信息存在一定的误差,且PSO算法误差大于萤火虫算法,而在电阻率较低的第二层和第四层中,两种算法误差较小。从图4b可以看出,在前6次迭代中,萤火虫算法的误差大于PSO算法的误差,但是萤火虫算法的收敛速度比PSO算法快;通过迭代计算,萤火虫算法的误差逐渐低于PSO算法,并趋于稳定值。

a. 反演曲线;b. 目标函数随迭代次数变化曲线。

a. 反演曲线;b. 目标函数随迭代次数变化曲线。
表1和表2给出了两种非线性优化算法的反演结果和相对误差。从表1可以看出:在三层地电模型中,PSO算法对第一层电阻率的反演精度好于萤火虫算法,但随着层数增加,PSO算法误差逐渐大于萤火虫算法;而在四层地电模型中,除了第三层之外,PSO算法的反演精度均优于萤火虫算法。从表2可以看出,PSO算法反演深度的误差整体上大于萤火虫算法。因此,可以说明PSO算法对地层深度信息的反演精度较差。
在算法的计算时间方面,当迭代次数为60次时,PSO算法处理三层地电模型需要6.50 min,萤火虫算法需要48.00 min。在处理四层地电模型时,PSO算法耗时7.60 min,而萤火虫算法耗时约113.20 min。与上述两种算法的计算时间相比,“烟圈”快速成像方法的计算时间几乎可以忽略不计(表3)。
3.2 含噪声理论数据反演
在实际工作中,采集到的信号可能包含各种噪声信号,会导致处理结果不稳定。因此,有必要分析算法的抗噪能力。将5%和10%的高斯随机噪声(图5a)添加到四层理论地电模型中,并使用PSO算法和萤火虫算法进行处理。图5b、c为含噪四层地电模型的反演结果。从图5b可以看出,当添加随机噪声时,PSO算法和萤火虫算法都可以反映理论模型的电阻率和深度信息,但结果逐渐偏离理论模型参数。从图5c可以看出,无论在哪种噪声下,萤火虫算法的目标函数总是可以快速收敛到一个较小的稳定常数,而PSO算法的目标函数值在迭代计算中远远大于萤火虫算法,且噪声越大,目标函数值越大。因此,可以分析得出萤火虫算法的收敛性优于PSO算法。

表1 两种非线性优化算法电阻率反演结果

表2 两种非线性优化算法深度反演结果

表3 算法计算时间对比表

a. 含噪磁场强度垂直分量;b. 含噪反演曲线;c. 目标函数随迭代次数变化曲线。
表4和表5为两种非线性优化算法处理含噪数据的结果和相对误差,可以看出,无论在哪种随机噪声下,萤火虫算法的误差整体上小于PSO算法,这表明萤火虫算法的抗噪能力优于PSO算法。
4 实测数据处理
将PSO算法和萤火虫算法应用于某城市地铁线路岩溶勘察。该项目调查的目的是寻找隧道下方和周围潜在的岩溶分布。 调查区浅表层为第四系覆盖层,地层深部岩性为完整性较好的灰岩。TEM测线约40 m,各测点间距2 m。
图6为瞬变电磁多测道图。从图6可以看出,瞬态电磁信号在1.498 4~6.157 6 ms之间呈现增加趋势,说明是低阻异常体的反映。图7为“烟圈”快速成像方法、PSO算法、萤火虫算法的反演结果。PSO算法和萤火虫算法处理每个测点的数据分别需要5.00和8.50 min。从图7可以看出,与PSO算法和“烟圈”快速成像方法的处理结果相比,萤火虫算法反演得到的低阻异常范围更小,异常细节更加突出,具有较好的分辨率。
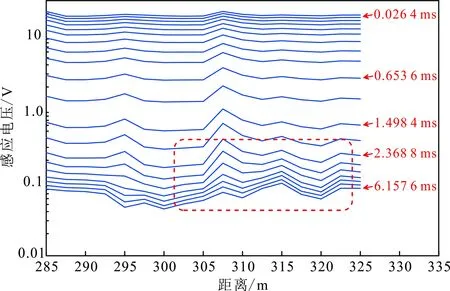
图6 瞬变电磁多测道图

表4 含噪四层地电模型电阻率反演结果

表5 含噪四层地电模型深度反演结果

a. “烟圈”快速成像方法;b. PSO算法;c. 萤火虫算法。
5 结论
本文采用PSO算法和萤火虫算法进行瞬变电磁数据反演,取得以下结论。
1)建立典型的三层和四层地电模型,分析两种算法的收敛特性和抗噪特性。研究结果表明:PSO算法计算效率高,但数据反演精度低,抗噪能力差;萤火虫算法在抗噪性、数据反演精度等方面均优于PSO算法。
2)利用PSO算法和萤火虫算法对岩溶调查实测数据进行反演处理。结果表明:萤火虫算法反演得到的低阻异常体细节较突出,分辨率较高。研究内容为TEM数据反演提供了新的方法和手段。
