基于支持向量机的可控源电磁数据智能识别方法

李 广，丁 迪，石福升，邓居智，肖 晓，陈 辉，何柱石，桂团福

1.江西省防震减灾与工程地质灾害探测工程研究中心(东华理工大学)，南昌 330013 2.有色金属成矿预测与地质环境监测教育部重点实验室(中南大学)，长沙 410083

0 引言

可控源电磁法(controlled-source electromagnetic method，CSEM)利用人工源电磁信号代替天然的交变电磁场作为场源，具有抗干扰能力强、勘探深度较大等优点，近年来被广泛应用于页岩气勘探、金属矿勘探以及工程物探等领域[1-2]。但随着人文活动范围的持续扩大，CSEM数据受人文噪声的干扰越来越严重，因此对观测到的数据进行噪声压制变得越发重要[3-4]。

为改善勘探效果，国内外学者提出了多种方法处理人文噪声干扰。例如：基于时变双边滤波的海洋可控源电磁数据噪声压制方法[5]；基于有理函数滤波的可控源音频大地电磁信号[6]及广域电磁法(wide-field electromagnetic method，WFEM)信号处理方法[7]；基于小波变换(wavelet transform，WT)的瞬变电磁信号去噪方法[8]；基于经验模态分解(empirical mode decomposition, EMD)的激电信号[9]及长偏移距瞬变电磁信号去噪方法[10]；基于字典学习的航空瞬变电磁数据[11]及广域电磁数据去噪方法[3]；基于相关度的激电信号筛选法[9]及基于灰色判别准则的广域电磁数据筛选方法[7]等。其中，数据筛选方法通过一定的评价标准从观测数据中挑选出质量较高的数据，而不必改变信号原有的形态；因此既不会损伤有用信号，也不会引入新的噪声，处理结果可信度高，在实际的数据处理中应用最为广泛。多数情况下，以上列举方法均能够显著地提高数据质量，但其也存在一定的局限性。例如：基于EMD的数据处理方法会因为EMD的模态混叠效应产生一定的误差；基于相关度的数据挑选法需要人工设定阈值，难以实现自动化的批量处理，且该方法要求操作人员具有一定的经验，易造成主观偏差。

近年来，随着人工智能技术的飞速发展，机器学习算法在地球物理领域得到广泛关注。支持向量机(support vector machine, SVM)是众多机器学习算法中的典型代表，它是在统计学习理论的基础上提出的一种模式识别方法，具有良好的泛化能力，特别适合于小样本分类等应用场合[12]。可控源电磁法所使用的信号是周期信号或者变频的多周期信号，每一个周期的时间序列均可以视为一个样本，但有时为了节省成本，可控源电磁信号观测时间较短，观测的样本数量较少，因此利用在小样本情况下具有优异表现的SVM算法对可控源电磁信号进行挑选是极为恰当的。为此，本文尝试将SVM引入CSEM数据筛选，代替传统的基于人工设定阈值的筛选法，以消除人工干预所带来的主观偏差，提高数据筛选的自动化程度与精度。

1 方法原理

可控源电磁数据中的人文噪声主要包括随机噪声、冲击类噪声以及基线漂移干扰等。其中：随机噪声幅度较小，多数情况下，通过多个周期的数据叠加并取平均值可以较好地压制随机噪声的影响；冲击类噪声包括脉冲噪声、方波噪声等，它们具有幅度大、能量强等特点，是一类对可控源信号的信噪比具有较大影响且现有方法难以去除的噪声；基线漂移干扰是可控源电磁数据中极为常见的一种持续性低频干扰，往往会造成视电阻率低频部分严重畸变。现有的文献[1,3]表明，利用互补集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD)可以较好地校正基线漂移。本文基于可控源电磁信号周期性的特征，结合CEEMD与SVM，提出了压制可控源强噪声的CEEMD-SVM方法，即在CEEMD处理之后，采用SVM识别出受到脉冲、方波等噪声污染的片段并予以丢弃，达到消除噪声的目的。

1.1 CEEMD

互补集合经验模态分解由经验模态分解和集合经验模态分解(ensemble EMD，EEMD)改进而来。集合经验模态分解通过给待分解数据添加白噪声的方式，较好地克服了经验模态分解的模态混叠问题，但加入的白噪声会对原始数据造成一定的污染。互补集合经验模态分解则通过添加成对且互补的白噪声，有效地消除了添加白噪声的影响。EMD以及CEEMD等算法均被用于可控源电磁数据的基线漂移校正，限于篇幅，本文对CEEMD的原理部分不再赘述，详情可以查阅文献[3,13]。

1.2 支持向量机

支持向量机是由前苏联学者Vapnik最早提出的一种基于统计学习理论的新型学习机，它是一种二类分类模型，是定义在特征空间上的间隔最大的线性分类器[14-15]。SVM目前已被应用于大地电磁信噪识别[16]、地震体波震相的自动识别与拾取[17]、地震事件分类[18]和岩性识别[19]等领域。假定一个特征空间上的训练数据集Q={(x1,y1),(x2,y2),...，(xN,yN)}, 其中xi为第i个特征向量[12]，也称为样本，yi为xi的类标记，xi∈Rn,yi∈{-1,1}，i=1,2,...,N。支持向量机的学习目标是在特征空间中找到一个分离超平面，能将实例分成不同的类。分离超平面(w,b)对应于方程[20-21]：

w·x+b=0。

(1)

式中：w为超平面的一个法向量；b为截距，用来确定超平面的具体位置。对于给定的训练数据集Q和超平面(w,b),定义超平面(w,b)关于样本点(xi,yi)的函数间隔为

ξi=yi(w·xi+b)。

(2)

函数间隔ξ的取值并不影响最优化问题的解，本文取ξ=1。一般地，将寻找最优超平面的问题转化为最优化问题

且满足

yi(w·xi+b)-1≥0,i=1,2,…,N。

(3)

这是一个凸二次规划问题，如果求出约束最优化问题式(3)的解w*,b*,那么就可以得到最大间隔分离超平面。应用拉格朗日对偶性，通过求解对偶问题可得到原始问题的最优解。构建拉格朗日函数，对每一个不等式约束，引进拉格朗日乘子αi≥0,i=1,2,...,N，定义拉格朗日函数为

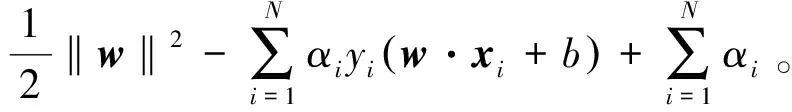
(4)

式中，α=(α1,α2,…,αN)T为拉格朗日乘子向量。

根据拉格朗日对偶性，原始问题的对偶问题是极大极小值问题：

(5)

所以，为了得到对偶问题的解，需要先求L(w,b,α)对w,b的极小，再求对α的极大。

求解得：

(6)

(7)

将式(6) 及式(7)代入拉格朗日函数式(4),即得

(8)

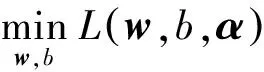
且满足

(9)

对线性可分的训练数据集，求得对偶性最优化问题，其中，式(9)中的α解为α*=(α1*,α2*,…,αN*)T，可以由α*求得原始最优化问题，对(w,b)的解w*,b*，有:

(10)

(11)

由此可知，分离超平面可以写成

(12)

求得相应的分离超平面后，再利用高质量信号与低信噪比信号之间的参数差异，将高质量信号分为正类，低信噪比信号分为负类，将二者分离，达到噪声压制的效果。

1.3 特征参数

特征参数指在信号筛选时，能够评价信号质量或者衡量受噪声污染程度的指标。本文采用了4个特征参数，包括观测信号的最大值、样本熵、相关度及分形盒维数。

1.3.1 最大值

可控源电磁信号为多周期的时间序列，当没有受到噪声污染时，每一个样本其幅度的最大值都是相同的。当某一个样本受到脉冲等强冲击类噪声污染时，其最大值明显大于其他样本，因此最大值可以用于识别受到脉冲等冲击类噪声污染的样本。

1.3.2 样本熵

样本熵(sample entropy，Es)在定义上与近似熵十分接近。两者均通过测量信号中生成新模式的可能性来比较时间序列的复杂性。与近似熵相比，样本熵具有两个优点：一是样本熵的计算可以脱离对数据长度的依赖，二是样本熵比近似熵有更强的一致性。样本熵的值越小，序列的相似程度越高；样本熵的值越大，样本的序列越复杂。目前，样本熵已经被应用于大地电磁信噪辨识[22]以及生物医学信号分析[23]等多个领域的研究中。其定义如下：

1)设原始数据为{xi}={x1,x2, ...,xn}，长度为n。预先给定嵌入维数m和相似容限r，依据原始信号重构一个m维向量X(i)=[xi,xi+1, ...,xi+m-1]。

2)定义x(i)与x(j)间的距离dij为两者对应元素差值绝对值的最大值，即

dij=d[x(i),x(j)]=
max[|x(i+k)-x(j+k)|] 。

(13)

(14)

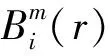
(15)

6)理论上，原始序列的样本熵定义为

(16)

当n为有限数时，上式可表示为

ES(m,r,n)=lnBm(r)-lnBm+1(r)。

(17)

1.3.3 相关度

利用发送信号与观测信号时间域波形的因果关系，引入相关度分析进行激电信号的筛选[1]。但计算时间域波形的相关度时，时间序列的相位需要严格同步，操作起来多有不便。CSEM法使用的信号为周期信号，并且信号稳定度很高，同一次发射的信号，只要数据长度相同，不管相位如何变化，其频谱都是相同的。因此，本文通过转换到频率域进行归一化互相关度分析解决上述困难。对于采样点长度为N的观测信号频谱序列Rλ及相同长度的发送信号频谱序列Tλ，二者的归一化互相关度(normalized cross-correlation,CNC)可利用Pearson相关系数[3,9]表示：

(18)

1.3.4 分形盒维数

本文采用的第4个参数是分形盒维数(fractal box dimension,DFB)。分形理论由美籍法国科学家Mandelbrot B创立[24]，该理论用分形维数来度量不规则程度，揭示自相似特性，是一种能够刻画非线性系统行为的数字特征的参数。其核心思想是以一定尺寸的栅格来覆盖目标并记录所用栅格的数目，然后拟合出栅格尺寸与所用栅格数目之间的曲线，最后以拟合曲线的斜率表征目标的不规则度[25]。目前，分形盒维数已被广泛应用于裂隙多孔介质运输特性的评估[26]、微震及爆破事件的模式识别[27]和大地电磁信噪辨识[16,22]等领域。假设栅格的尺寸为ε，X是Rn的一个非空有界子集，M(X,ε)是实现目标X全覆盖所用的栅格数目，则目标X的分形盒维数可表示为

(19)

1.4 数据处理流程

本文所提的可控源电磁数据处理方法流程如图1所示。首先，导入观测到的实测数据；其次，利用CEEMD去除实测数据中的基线漂移噪声；随后，对时间序列进行分段(每一个时间序列片段即为一个样本，其长度为一个周期的时间序列)，并计算每一个样本的特征参数；最后，将样本的特征参数作为SVM的输入，利用SVM进行分类，筛选出高质量的时间序列。

图1 数据处理流程图

2 合成数据测试

2.1 样本库建立

样本库是SVM准确识别高质量信号的依据，良好的样本库应该包含有各种类型的高质量样本以及低信噪比样本。为使得样本库足够完善，同时为了剖析不同CSEM信号与噪声的特征，我们对不同类型的样本进行标记、分类，制作成样本库。样本库中包含高质量的CSEM信号以及受到方波噪声、脉冲噪声和基线漂移噪声等最为典型噪声污染的信号。每种类型各含有50个样本，共计200个。

分别计算每个样本的最大值、样本熵、相关度以及分形盒维数，并用这些参数来替换样本本身，用SVM对其进行分类。如图2所示，SVM将200个样本准确地分为2类，即高质量信号样本(类别标签1.0)和含噪声样本(类别标签2.0)。值得注意的是，如图2a和c所示，所有高质量信号样本的最大值都小于含噪声样本且都具有很高的相关度值，说明高质量样本的相关度都很高。但高的相关度值并不总意味着高质量，因为大多数有尖峰的样本和少量被方波噪声和基线漂移干扰污染的样本也具有非常高的相关度，这说明依靠相关度一个参数并不能准确识别所有的高质量信号样本，结合最大值这一特征则能够显著改善识别效果。如图2b和d所示，受方波噪声和基线漂移干扰污染的大多数样本的样本熵与分形盒维数显著大于高质量信号样本。因此，分形盒维数、样本熵可以识别被方波噪声或基线漂移噪声污染的样本，消除相关度可能无法准确识别这些样本所造成的误差。

2.2 数据合成

如图3所示：蓝色信号为一组高质量信号，为防止与其他信号重叠，便于直观显示，该信号整体向下平移了40 mV；黑色信号是添加有多种类型强噪声的合成信号；绿色信号为CEEMD提取的基线漂移噪声；红色信号是去除基线漂移后获得的信号。显然经过CEEMD处理后基线漂移现象得到明显改善，但正弦波、方波和三角波等噪声仍然严重影响数据质量，因此须进行下一步处理。

2.3 支持向量机智能识别挑选

对于去除基线漂移后的信号，首先根据信号的周期进行分段，并分别计算每一个片段的最大值、样本熵、相关度以及分形盒维数4个特征参数；然后将特征参数输入到SVM中进行信号的识别筛选。如图4所示，蓝色的点代表含噪片段，红色的点代表高质量片段。图4a中，高质量信号幅值分布相对稳定，代表信号不含强噪声，而含噪片段明显分布离散；图4b对应每个片段的样本熵，高质量片段所得样本熵几乎处在同一水平线上，而含噪片段则相对更加离散；图4c为相关度，可见高质量片段样本趋近于1，含噪片段样本偏离1，表示高质量信号相关度接近1；图4d为分形盒维数，可见高质量片段分形盒维数值趋于同一水平，且高于含噪片段。

如图5所示，SVM识别出来的强干扰段每一个周期均受到了方波、脉冲等强噪声的污染(图5a)，经过筛选，添加的噪声被消除(图5b)，未受到噪声污染的数据被筛选出来，留下的高质量段则不存在强噪声(图5c)。经过人工复核，SVM信噪识别的准确率为100%。需要提及的是，本例中的噪声幅度均大于其余有效信号，利用常规的阈值筛选法设定精确的阈值，也能准确地挑选出高质量信号。然而，实际情况中，不同的观测信号，其阈值并非固定不变，常规的阈值法需要操作人员通过多次试探才能找到最佳的阈值，因此，常规的阈值法无法实现自动化的批量处理。此外，通过多次试探获得最佳阈值的过程不仅耗时较长，还会因不同的操作人员设定不同的阈值得到不同的处理结果，造成主观偏差。

a. 最大值分类效果；b. 样本熵分类效果；c. 相关度分类效果；d. 分形盒维数分类效果。类别标签1.0表示高质量信号样本，2.0表示含噪声样本。

图3 CEEMD校正基线漂移效果

为定量评估本方法的去噪效果，对7个主频进行了误差分析，表1为图6中信号去噪前后的误差统计。由表1的统计数据可知：加入噪声后信号的幅值与真实值的误差最高达到35.98%，其他频点误差大小也在1.12%～11.94%之间；经过CEEMD去噪处理之后最大误差绝对值达到7.51%，其他频点误差绝对值在0.12%～4.83%之间；再经过SVM识别筛选后，除0.75 Hz一个频点外，其余频点误差均小于1.00 %。合成数据处理结果充分说明了本文所提方法的可靠性与有效性。

分别对原始信号、加噪信号和处理后的信号进行快速傅里叶变换，得到的频谱见图6。由图6分析可知，加入噪声后大部分的频点受到了污染，低频部分受污染情况尤为突出。经过所提方法处理后，频谱曲线被校正，其形态与原始信号的频谱差异较小。

图4 最大值(a)、样本熵(b)、相关度(c), 以及分形盒维数(d)区分效果

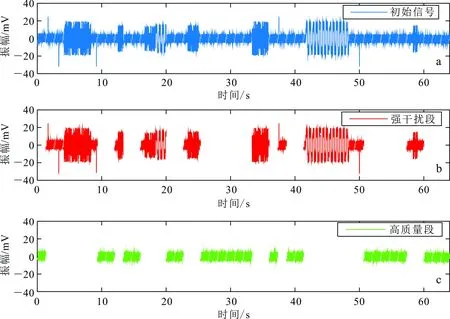
图5 合成信号SVM处理前后的时域图对比

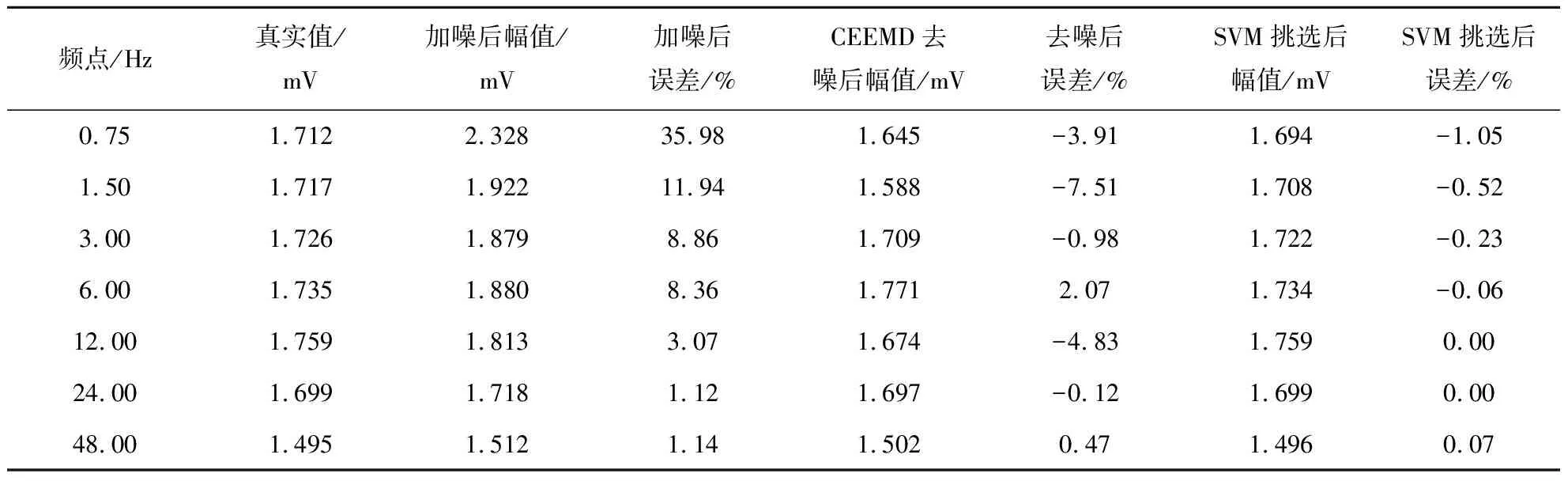
表1 去噪前后有效频点幅度误差统计

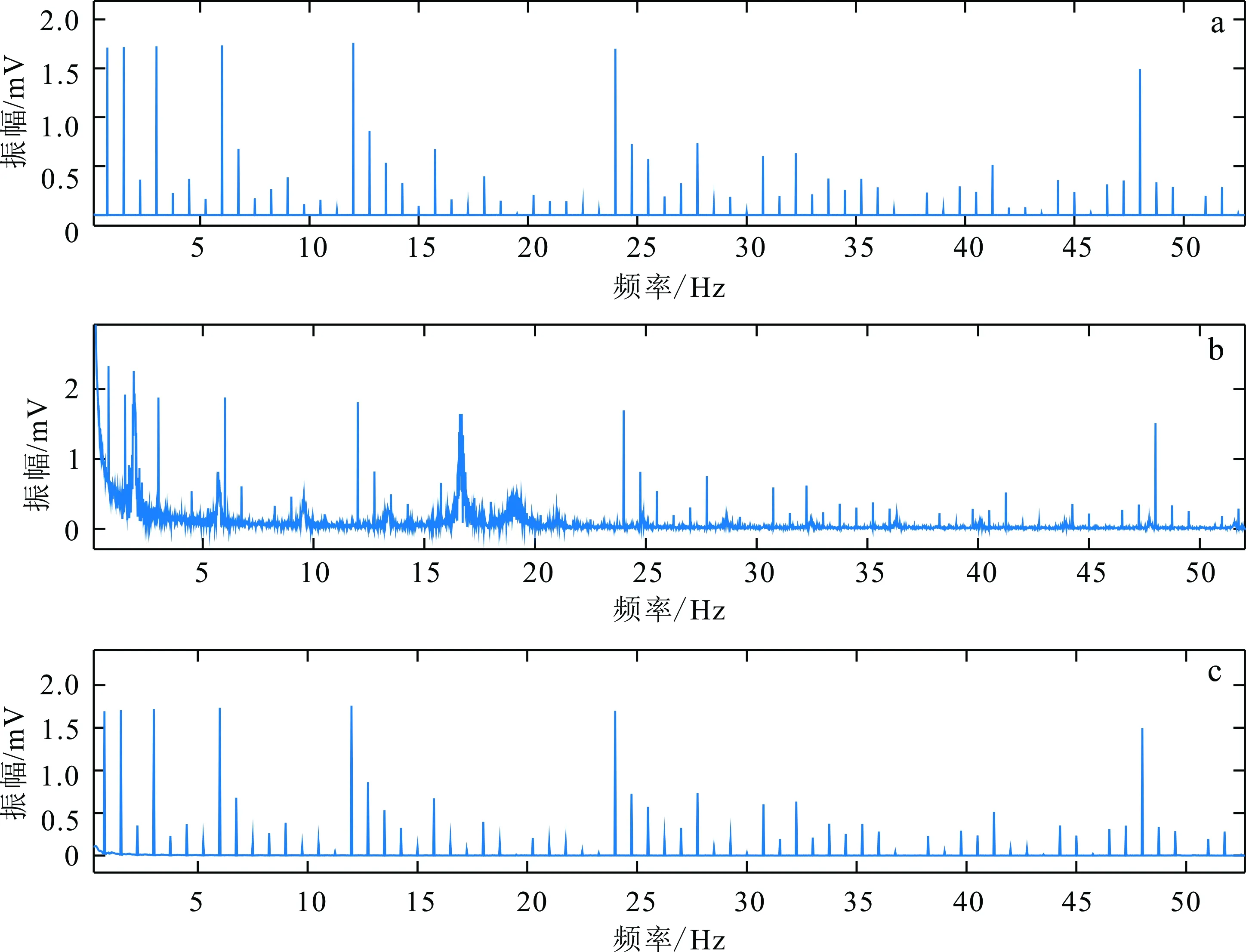
a. 原始信号; b. 加噪后; c. 处理后。

3 实际案例分析

3.1 时间域

在四川省会东县城郊进行广域电磁法勘探时，由于观测点距离县城较近，采集到的数据受到了强烈的人文噪声污染。为提高数据质量，应用本文提出的CEEMD-SVM方法对观测数据进行处理。

如图7所示：该测点采集的信号在前30 s受到了严重的人文噪声污染，75 s和85 s前后的信号也受到了严重的干扰，60 s和95 s附近还有零星的强干扰(图7a)；SVM准确识别出了所有的强噪声片段，仅有55 s处个别噪声较弱的片段没有被识别出来(图7b、c)；相关度法的识别效果明显不如SVM，60 s和95 s附近的强干扰片段(图7b中已识别)以及55 s处的弱干扰片段均没有被识别出来(图7d)。

如图8所示，与人工标记的实际分类结果相比可知，SVM的识别准确率达到94.79%。尽管有少数噪声幅度较弱的样本没有被识别出来，但由于噪声幅度弱，且高质量样本数据占比很高，这些含有弱噪声的样本对最终的结果影响不大。经过对四川会

a. 初始信号; b. SVM识别出的强干扰段; c. SVM识别出的高质量段；d. 相关度法识别出的高质量段。

类别标签1.0表示分类结果为高质量信号样本，2.0表示分类结果为含噪样本；蓝色圈为人工标记的实际分类结果，红色星号为SVM预测的分类结果。

图8 实测点L1-3时间序列SVM分类与人工标记结果对比

Fig.8 Comparison of SVM classification and manual labeling results for real site L1-3

东县工区多个数据进行处理，我们发现SVM的平均识别准确率在92.00%以上。如图7d所示，将相关度的阈值设定为0.91时，使用常规的数据筛选法也得到了良好的结果，筛选精度为92.71%。然而，得到0.91这一精确的阈值，需要经过多次尝试，且不论设定阈值多少，其精度均无法超过本文提出的CEEMD-SVM方法，从而说明了CEEMD-SVM方法的优越性。

3.2 视电阻率

为进一步评价信号处理结果的可靠性，对处理前后的CSEM数据进行了广域电磁视电阻率计算[28]，并与基于相关度的挑选法[9,29]进行对比，结果如图9所示。其中：图9a和f所示测点的视电阻率曲线出现严重畸变，视电阻率随频率的变化而剧烈波动；图9b和e所示测点视电阻率也有较明显的畸变，应用本文提出的CEEMD-SVM方法处理后，视电阻率曲线均得到显著改善，连续性大为提高；图9c和d所示测点的信号未受强噪音污染，处理前后的视电阻率曲线无明显变化，也就是说，CEEMD-SVM法既适用于有噪声的数据，也适用于无噪声的数据，因为它极大地提高了含噪信号的质量，并且不降低无噪信号的质量。基于相关度的挑选法也能够显著的提高数据质量，且多数情况下其结果与本文所提方法的结果一致性较好，从而说明CEEMD-SVM法处理结果可信度高。但由图9b和f所示测点处理结果可知，在视电阻率曲线的低频段部分，CEEMD-SVM法优于相关度挑选法;这是因为基于人工设定阈值的相关度挑选法仅考虑了发送信号与观测信号之间的相关度，依靠单一的参数得到的结果其可靠性显然具有较大的提升空间。此外，相关度挑选法需要操作人员有一定的经验，否则可能造成一定的主观偏差。

图9 四川会东县L1测线6个观测点处理前后的视电阻率曲线

4 结论与建议

1)本文基于可控源电磁信号周期性的特征，结合CEEMD与SVM，提出了压制可控源强噪声的CEEMD-SVM方法。其能够从受到强人文噪声污染的数据中准确地挑选出高质量的信号，有利于实测数据的批量化、自动化处理，减少了传统的基于人工设定阈值所带来的主观误差，降低了数据处理操作的复杂性与工作量。

2) CEEMD-SVM方法考虑了最大值、样本熵、相关度以及分形盒维数等4个参数，与传统的基于单一的相关度挑选方法相比，结果的可靠性更高。

3) CEEMD-SVM方法不会对高质量数据造成影响，其既适用于含噪数据，也适用于无噪数据，适用性较好。

4)可控源电磁法面对的人文噪声纷繁复杂，通常单一的信号处理方法都存在一定的局限性。当样本受到持续性的强冲击噪声污染时，数据筛选类的方法可能难以获得满意的结果。此外，在处理实测数据时，少数噪声较弱的样本没有识别出来，本文所提的CEEMD-SVM方法其识别精度并不能达到100%，识别精度仍有一定的提升空间。此外CEEMD-SVM方法仅识别出了受到强噪声污染的时间序列片段，没有识别出噪声的类型。根据噪声的特点，采取合适的信噪分离措施，如字典学习或者深度学习去噪等，可以保留更多周期的时间序列，并进一步提升数据质量，这是值得进一步研究的重要方向。