概率论与数理统计中“二项分布”的教学设计
2022-06-22王燕飞薛冬梅
王燕飞,薛冬梅
(吉林化工学院 理学院,吉林 吉林 132022)
自2014年习近平总书记在全国高校思想政治工作会议发表重要讲话以来,课程思政建设已经逐步深入人心。教育应以“立德树人”为本,培养有德、有志、有义、有信的人。概率论与数理统计是一门研究随机现象客观规律性的数学课程,具有独特的思想方法,广泛应用于生产生活中各个领域,也是高等院校一门重要数学基础课。教师应当以概率论与数理统计知识为载体,将思政元素和理念融入日常教学活动中,对教学过程、教学内容等进行重新整合和设计[1]。在以往的文献中多数是针对该课程思政元素融合的宏观设计和引领[2-7],而在具体的课程内容上,如何细致入微地融入思政元素是值得探究的。在概率统计理论与应用的研究发展史上,“二项分布”被认为是一种具有绝对统治性质的概率分布之一,且由于其应用的重要性和广泛性备受学者关注。在课程中起到了承上启下的作用,它既是前面所介绍的离散型随机变量中最常见的分布类型之一,又与后续另一离散型分布泊松分布及连续型分布正态分布有着密切联系,另外,在大数定律和中心极限定理这两个核心理论中,二项分布也占据重要地位。为此,从融入课程思政元素的角度,对“二项分布”知识点进行精心地教学设计,力图为教师讲解提供崭新的思路和启发。
一、教学目标
深刻理解二项分布的产生背景和概念,明确(0-1)分布是二项分布的特殊情况。掌握通过判别伯努利概型的方法和技巧,从而明确二项分布的随机变量取值概率的求解计算。培养学生从概率的角度分析实际问题,并利用概率知识解决问题的能力。
二、学情分析
学生初步掌握了离散型随机变量的概念及其分布列和分布律的表达形式。具备一定的归纳、抽象能力。但不足点是:对于分析和解决实际背景问题的能力相对薄弱,概率思维的运用及数学建模能力有待提高。
三、教学重点及难点
(一)教学重点
二项分布的判定、服从二项分布的随机变量的引入、利用二项分布求解实际问题。
(二)教学难点
伯努利概型的理解及判别技巧、二项分布中的两个参数的确定、用随机变量表示随机事件。
四、教学方法的设计
首先,提出女排比赛问题,引发学生思考,调动积极性进入“二项分布”的学习。并将这个案例贯穿教学全过程,通过解决女排比赛问题,由浅入深介绍“伯努利试验”“n重伯努利概型”“二项分布”及“(0-1)分布”的概念。其次,利用计算机程序画出二项分布取值概率的图像,直观理解概念,增强学生学习兴趣。另外,在案例分析过程中,从“二项分布”和“穷举法”两种思路求解,比较分析,开阔学生思路。最后,通过“二项分布”知识点的思维导图总结相关知识点的关系。
五、教学过程设计
(一)课程引入
那么,请同学们思考问题:如果中国和塞尔维亚女排再次交锋,获胜的概率有多大呢?
事实上,可以利用概率方法解决这个问题,为此,需要学习一种新的概率模型和概率分布。
(二)伯努利试验和n重伯努利试验
在世界上存在两种结果的事物有很多,比如:围棋的棋子是黑色或者白色、硬币的图案是正面或者反面、一场足球比赛有胜有负、抽检的产品是合格品或是次品、一门考试结果是及格或者不及格等等。在哲学中,辩证唯物主义认为事物总是有两面性的,它们既对立又统一。
在概率论与数理统计中,这样只有两种结果的随机试验我们称为伯努利试验[9]。而具有独立性、重复性(每次试验在相同条件下进行)的n次伯努利试验称为n重伯努利试验(或n重伯努利概型)。具有如下特征:

3.独立地重复进行n次试验。
其中,n次试验相互独立指的是各次试验的结果为何相互之间没有影响。“独立性”也是n重伯努利试验最重要的特征。
这类概率模型在生活中应用较为广泛,比如:一名特种兵在相同地点使用同一手枪多次射击打靶试验;一批产品有放回地抽检100件;奥运会乒乓球单打淘汰赛两名选手对打7局,每局只有胜负2个结果,且7局之间结果相互独立。这些都符合n重伯努利试验。
(三)二项分布
1.定义:在n重伯努利试验中,通常比较关心其中的一个结果(不妨设为A)发生的次数,设为随机变量X,则X的概率分布称为二项分布,记作X~B(n,p)[10]。此时X取值的概率为
(1)
注:(Ⅰ)二项分布的名称主要来源于其概率结果为二项式定理的展开式。缩写代表字母B既是伯努利(Bernoulli)名字开头,也是二项(binomial)的开头字母,而“bino”在计算机中代表二项的。在Matlab中提供了binopdf、binocdf和binoinv等语句分别用于求解二项分布的取值概率、累积取值概率和满足概率的左邻界值;
(Ⅱ)参数n为独立试验的次数,p为一次伯努利试验中A发生的概率值,k为在n次试验中A发生的次数X的取值。在具体的实际问题中,要注意如何判断是否为二项分布,重要的就是将问题背景中的量抽象成模型中的参数,即哪些是事件A,概率p,试验次数n及发生的次数X。这需要学生多次练习并熟练掌握;

2.推导
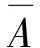

3.分布律图像
以参数n=100,p=0.03的二项分布B(100,0.03)为例,利用Matlab中的binopdf语句或者EXCEL中的BINOM.DIST.RANGE语句,均可求得随机变量X各个取值的概率,并画出柱状图,如图1所示。

X的取值
从分布律图像中不难发现,纵坐标的取值概率大致呈中间高两边低的拱形趋势,这一结果使得后来的学者研究出了二项分布与其他分布诸如泊松分布、正态分布之间的关系。这些内容在后续课程中再陆续介绍。
(四)人物介绍
雅各布·伯努利(1654-1705年),瑞士数学家,天文学家,是声望显赫的科学世家伯努利家族中的佼佼者。1699年,成为巴黎科学院院士。1701年成为柏林科学院会员。
众多的数学研究成果以“伯努利”命名。比如:1694年的伯努利双纽线,1695年的伯努利微分方程等。而他在概率论方面所做出的研究成果是其对数学领域最重要的贡献。他把一生所研究的成果最终著成不朽之作,这就是1713年出版的《猜度术》,提出了有史以来的第一个大数定律——伯努利大数定律。其主要表明的结果就是频率与概率接近关系,使得概率的统计定义具备理论依据。这一结果在概率论发展画卷上也是色彩亮丽的一笔,其影响及其深远。
(五)案例分析:女排比赛
下面从概率的思维角度分析两国交战的情况。根据数据统计,中国女排与塞尔维亚女排历史交锋共19次,总比分为43:37。则对于每局对决,中国女排获胜的概率约为0.54,输掉的概率约为0.46。赛制为五局三胜,那么中国女排最终取得胜利的概率有多大呢?

2.问题求解:解法一:利用二项分布计算。
假设随机变量X为在总局数为5局比赛时中国女排的获胜次数,则X~B(5,0,54)。根据5局3胜制,要想最终取得胜利,至少赢得3局,即获胜的局数分别可能为3、4、5。假设事件C={女排赢得比赛胜利},则
由此,计算出了中国女排最终战胜塞尔维亚女排的概率约为0.57。
这种方法简单易求,但有的结果或许和的直觉想法有出入。比如,如果前三局比赛都获胜了,实际情况是我们不需要再打后两局了,如此看来,获胜5局的情况是不存在的。那么,这种求解方法正确吗?下面不妨利用常规思路再求解一下,比较二者结果是否一致。
解法二:穷举法。
考虑实际比赛中,女排最终获胜的所有可能情况共10种,具体情况见下表1。

表1 女排最终取胜的实际比赛可能情况统计表
由于各局比赛结果相互独立,则可得:
3.思考问题:为何两种方法考虑角度不同,所得结果却是一样的?
分析:按照解法一中在5局比赛中获胜局数分别为3、4、5时考察所有比赛的情况,对比解法二中的实际比赛局数。具体见表2。

表2 两种解法的比赛情况对比表

即解法一和解法二是一致的。

当获胜局数为5局时,实际比赛局数为5局共6种情况,对比表1和表2完全相同。因此,尽管考虑的角度不同,两种方法都可以用来就解,所得结果是一致的。而相比穷举法,利用二项分布求解起来直观简便,何尝不用。因而,此类问题不需要再费尽精力一一考虑所有可能情况,直接利用二项分布求解即可。

伯努利试验体现的是一次试验只有两个结果。而人生中很多事都不是只有胜和负这两种结果,自古以来不以成败论英雄,重要的是为了心中的理想努力奋斗过。青春的意义正是如此,每个人都应该有一个长远的目标,并脚踏实地为之刻苦拼搏。能够淡定的收获战果,也应该同样坦然的接收失败,并在失败中总结教训,不断进取!希望同学们能发愤图强,励精图治,报效祖国!
5.问题拓展:同学们可以课下查阅资料,用概率方法分析中国女排和另一个世界强队美国女排的对决情况,考虑中国女排获胜的概率有多大?
通过以上思维导图总结,如图2比较容易理解“伯努利试验”和“n重伯努利试验”的主要特征及其与“(0-1)分布”和“二项分布”之间的密切关系。

图2 知识梳理的思维导图
六、教学创新点
本文针对“二项分布”这一知识点,对教学过程进行设计。主要创新点包括:
1.从“女排比赛”问题引入,引起学生学习兴趣;
2.在案例分析求解过程中,通过两种方法的比较研究,拓宽思路,培养学生的概率思维能力;
3.利用Matlab数学软件画出二项分布律的图像,更加直观,同时为后续课程“泊松分布”及“正态分布”的学习做好铺垫。另外,通过数学软件的操作,使得学生对于知识的理解更加深刻;
4.对于数学家伯努利的介绍,开阔了学生视野,培养学术研究素养;
5.解析“女排精神”,恰当融入“思政元素”,引领学生树立正确的人生观和价值观;
6.利用思维导图总结,使得学生深刻理解各概念之间的关系,直观明确。
七、教学反思
通过“女排比赛”问题,使得学生对于“二项分布”“(0-1)分布”“伯努利试验”及“n重伯努利试验”理解透彻。利用数学软件操作,启发思考问题和思政引领等方式,学生表现出较高的积极性和较大的情感投入,通过提问和互动表明学生已经获得良好的学习效果,达到了本节的教学目标。
