基于内聚力模型的含畸形骨料混凝土单轴受拉细观模拟研究
2022-06-22张小飞肖天培
张小飞,田 羽,覃 培,肖天培,吴 健
(1.广西大学土木建筑工程学院,广西 南宁 530004;2.中国电建集团北京勘测设计研究院有限公司,北京 100024)
0 引 言
混凝土是目前最主要的工程材料之一,是一种由胶凝材料、骨料、水及外加剂按一定比例组成的多相混合材料。自19世纪20年代波特兰水泥问世后,混凝土发展至今已有200年,人们对其性能的研究从未间断,随着科技的不断创新与发展,有关混凝土的研究已从传统的宏观分析发展到宏观、细观、微观分析多种途径和方法。张楚汉等[1]认为混凝土从宏观,再到细观乃至微观是一个息息相关的整体,只有对混凝土在不同尺度下的损伤演化机理进行研究,从整体到局部、从宏观到微观,才能进一步了解混凝土的变形力学性能。
基于各类有限元软件的数值模拟作为一种新研究途径,目前被广泛应用混凝土细观层面的模拟研究,学者们提出了诸如格构模型[2]、随机骨料模型[3]、M-H模型[4-5]、随机力学模型[6]等一系列细观模型,虽然这些细观模型能较好地模拟出裂缝的损伤扩展情况,但对网格的敏感性大且计算难以收敛[7]。
近些年来在有关混凝土裂纹扩展方面的研究中,一种名为内聚力模型的细观力学模型开始被学者们所关注,其主要是将混凝土划分为三相:砂浆、骨料以及骨料与砂浆组成的粘结面,骨料和砂浆为实体单元,骨料-砂浆粘接面为内聚力单元,采用牵引力分离准则对内聚力单元的损伤及破坏过程进行判定[8-9],其优点在于不仅支持多条裂纹的扩展,同时可以避免裂纹尖端的应力奇异性,计算易于收敛。
目前基于内聚力单元的细观力学模型已开展了一系列相关研究,其中主要有:对骨料形状及占比的研究[7,10]、骨料-砂浆粘结面力学性能的研究[8]、骨料的随机分布形式的研究[11]等,以上研究不乏对骨料形状的研究,但均将骨料考虑为优质骨料,有关畸形(针状)骨料对混凝土整体力学性能影响的研究较为缺乏[12]。
本文基于内聚力模型的模拟计算方法,选取了骨料的长宽比、骨料在混凝土中的占比、骨料在混凝土中所处的级配作为变量,对含畸形骨料的二级配混凝土在单轴拉伸下的损伤与破坏过程进行系统的模拟计算,研究含畸形骨料混凝土在单轴受拉时细观与宏观间的响应与关联,并进一步探究3个变量对混凝土性能的影响程度。

图1 骨料投放流程
1 内聚力模型的生成
1.1 模型的生成
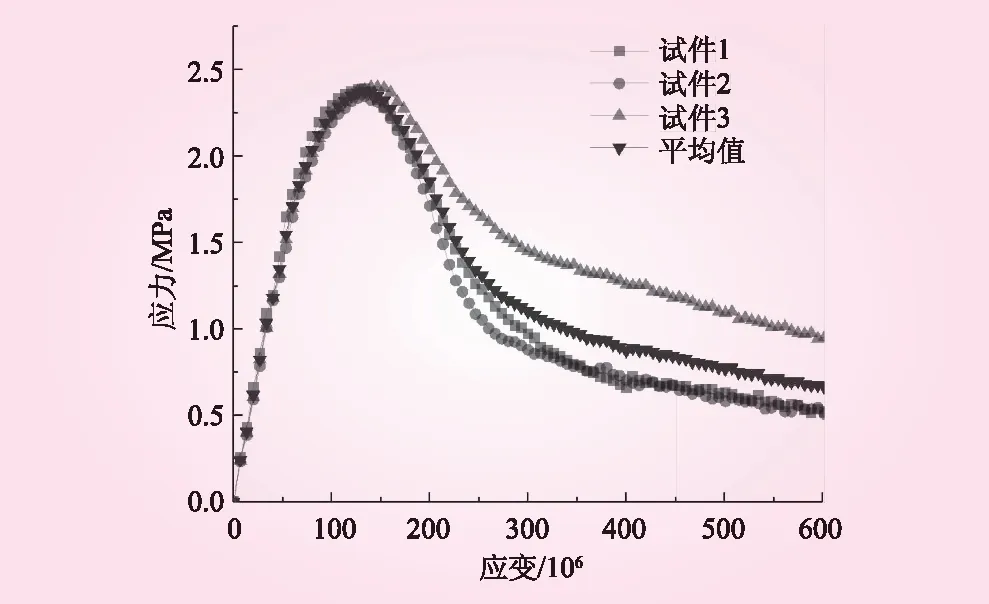
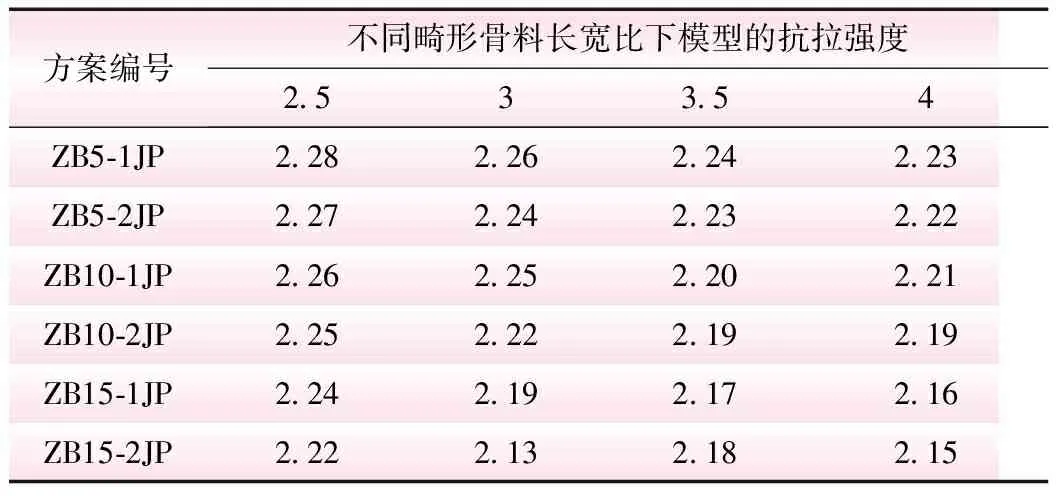
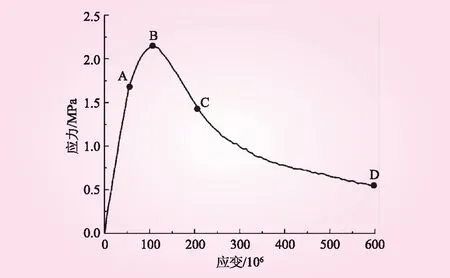
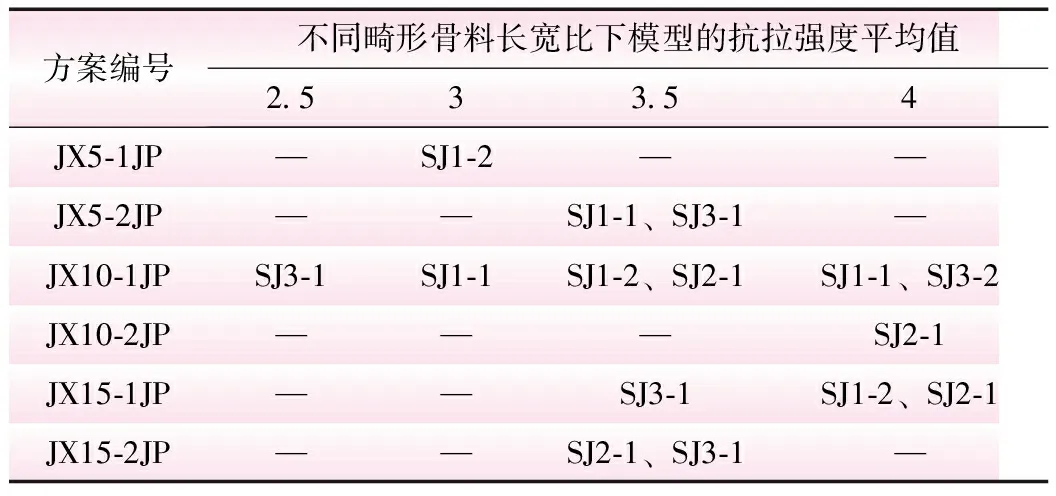
基于内聚力模型理论,本文将混凝土考虑为砂浆、骨料及骨料-砂浆组成的粘结面,其中对于直径小于5 mm的细骨料视作砂浆。针对混凝土在三维中的骨料分布如何向二维进行转换,瓦拉文[13]提出了一种转换公式,基于该公式可以将随机骨料模型应用于二维平面的模拟。瓦拉文公式提出在二维平面的指定范围内含有骨料颗粒直径D (1) 式中,Pc为各级配骨料在二维平面中出现的概率;Pk为骨料占二维截面面积的百分比;Dmax为最大骨料的颗粒直径;D0为某一级配骨料的颗粒直径。 骨料生成方法主要参考文献[14]的公式。其中,优质骨料主要通过极坐标随机生成每个骨料顶点的极半径和极角,表达式为[14] (2) 式中,R为骨料第i个顶点的极半径;r为某级配下骨料的代表粒径;alpha为骨料第i个顶点的极角;i为骨料的第i个顶点;n为骨料边数,取5~12之间的随机数。 对式(2)进行改进,用以生成畸形(针形)骨料,该表达式为 (3) 式中,a为控制畸形骨料长、短边比例的系数;b为基于旋转中心的转动角度,取值范围为0~π。 根据式(1)~式(3),可分别生成优质骨料和畸形骨料的骨料库,在确定二维混凝土模型的尺寸、骨料的级配及各级配骨料占比后即可进行投放,具体的投放流程见图1[14]。 1.2.1 实体单元本构 本文的骨料及砂浆均采用实体单元进行模拟,采用线弹性本构关系,单元类型选用平面应力三角形单元进行划分网格。 1.2.2 内聚力单元本构 在通常情况下混凝土受外荷载会产生随机的裂纹扩展,在骨料内部、骨料-砂浆粘结面及砂浆内部均有可能开裂,为保证模型更切合实际,本文的骨料-砂浆粘结面、骨料内部及砂浆内部单元均采用内聚力单元来模拟。内聚力单元模型主要假设在混凝土产生裂纹前,在其真实的裂纹尖端周围存在一个断裂过程区,该区域处于一个“断而未断”的阶段,该区域的损伤演化采用牵引力分离准则来表示,用单元张开的位移与应力之间的关系来描述单元从初始损伤直至最终破坏的过程。目前常用的牵引力分离准则有双线型、梯型、指数型等[15],本文采用双线型牵引力分离准则来模拟混凝土的断裂。 表1 材料参数 混凝土在单轴受拉情况下主要发生以I型断裂为主,同时伴有II型断裂的混合型断裂,因此,采用平方名义应力准则能更为准确地描述单元的起始损伤,其公式为[14] (4) 内聚力单元的损伤演化选取适用于I、II混合型断裂模式的Benzeggagh-Kenane(B-K)断裂准则,即 (5) 建立好模型后,首先进行参数校调。采用王仲华等[16]以石灰岩作为骨料的28 d龄期二级配混凝土试验成果,以抗拉强度及抗拉弹性模量为指标对数值模型进行参数标定,该试验所得二级配混凝土抗拉强度平均值为2.36 MPa,抗拉弹性模量为37.7 GPa。采用试错法不断修正单元材料参数直至与物理试验结果相吻合,为后续探究不同掺量畸形骨料对二级配混凝土抗拉强度的影响作参照。共创建3组150 mm×150 mm的二级配混凝土试件作为参数校调对象,根据3组试件模拟结果的平均值视为最终校调结果。 试件采用位移加载方式,选取试件顶部节点施加位移荷载;约束方式采用位移约束,对试件底部节点施加竖向位移约束,并对底部中心节点施加水平位移约束。参校调后的材料参数见表1。 图2给出了模型参数校调后3个二级配混凝土试件的单轴拉伸应力-应变曲线,3个试件的抗拉强度最大值分别为2.39、2.35、2.40 MPa,抗拉强度平均峰值应力为2.37 MPa,抗拉弹性模量为35.75、35.2、35.4 GPa,平均值为35.5 GPa,相比试验数据[16],抗拉弹性模量最大误差为5.8%;抗拉强度平均值最大误差不超过0.04%,表明本文模型的参数校调取得了良好的效果。 图2 单轴拉伸应力应变曲线 2 二级配含畸形骨料混凝土单轴受拉细观模拟 建立含畸形骨料混凝土模型方案,主要思路为对混凝土某一级配中的优质骨料根据占比,将其替换为相同占比的畸形骨料。选取Ck分别为2.5、3、3.5、4,Zb分别为5%、10%、15%,Jp分别为1、2作为变量,建立24种模型方案,每种方案建立3个模拟试件,求解后取其平均值作为该方案的最终模拟结果。 24种模型方案的抗拉强度平均值见表2。 为分析试件的单轴受拉全过程,选取方案“Ck=3.5、Zb=10%、Jp=1”第1个试件为例进行分析,单轴拉伸应力-应变曲线见图3,其中选取了A、B、C、D等4个具有代表性的特征点,分别对应图4的4个损伤演化阶段。 由图4可知: (1)阶段A。由于骨料和砂浆在力学性能上的差异性,导致骨料-砂浆表面单元已经开始产生损伤,聚集出了类似“枣核状”的微裂纹,这些微裂纹扩展方向大致与荷载施加的方向呈90°,此时混凝土还处于弹性阶段,并未发现存在骨料内部发生损伤。 表2 各模型方案抗拉强度平均值 MPa 图3 单轴拉伸应力-应变曲线 图4 各阶段损伤演化示意 (2)阶段B。该阶段骨料-砂浆交界面的微裂纹逐渐向周围砂浆区域扩展的趋势,在混凝土内部形成了一条较为连续的微裂纹带,在微裂纹带的扩展路径上发现了两颗畸形骨料产生了损伤,主要集中在骨料的端部,并且有将骨料折断的趋势。 (3)阶段C。该阶段混凝土内部已大致形成一条主裂纹带,有部分受损单元完全失效而被删除,这也象征着微裂纹逐渐发展成熟,即将形成宏观上的裂纹带。此时左边受损的骨料的裂纹继续扩展,导致其相邻的一颗骨料也受到损伤。 (4)阶段D。该阶段混凝土内部已形成了一条宏观裂纹带,此时裂纹带附近的大部分受损伤单元已完全失效,其扩展方向大致与所受荷载的方向垂直。观察图中的受损骨料局部图可以发现,左边的两颗骨料已完全产生断裂,最右边的一颗相较之前有进一步断裂的趋势,但仍处于损伤阶段。 为分析畸形骨料各变量对混凝土性能的影响情况,将各模型方案中骨料的破碎情况(指骨料内部单元完全失效的情况)进行了统计分析,各方案试件均未发现优质多边形骨料发生破碎,畸形骨料破碎结果见表3。 表3 各模型方案抗拉强度平均值 MPa 由表3可知,畸形骨料的破碎情况展现出一定的规律性,当Ck越大、Zb越大、Jp越小时,产生骨料破碎试件的个数越多,但单个试件中骨料破碎的个数并未有明显的增加。这主要是由于:当Ck越大时,畸形骨料的棱角更为鲜明,其尖端部位在受拉过程中更容易产生损伤破碎;当Zb越大时,混凝土内部含畸形骨料的个数就越多,因此更容易产生畸形骨料破碎;而随着Jp的增大,骨料破碎的几率呈现出降低的趋势,原因可能在于畸形骨料的尺寸越大,所能承受的荷载就越大,更不容易产生断裂。 为进一步探究Ck、Zb、Jp这3个变量对二级配混凝土抗拉强度的影响权重,根据表2统计的各模型方案模拟结果,以Ck、Zb及Jp作为自变量,抗拉强度为因变量,进行多元线性回归分析,得到回归方程为 y=2.433-0.039x1-0.007x2-0.017x3 (6) 式中,y为二级配混凝土的抗拉强度;x1为畸形骨料的长宽比Ck;x2为畸形骨料的占比Zb;x3为畸形骨料的级配Jp。 由式(6)可知,3个自变量对二级配混凝土抗拉强度的影响权重表现为Ck>Jp>Zb。 本文从细观力学的角度出发,选取了畸形骨料的长宽比Ck、畸形骨料在混凝土中的占比Zb、畸形骨料在混凝土中所处的级配Jp作为变量,探究3个变量对二级配混凝土抗拉性能的影响。得出以下主要结论: (1)Ck、Zb、Jp3个变量对二级配混凝土的抗拉强度均产生一定程度的影响,大致表现为Ck越大、Zb越高、Jp越大时,混凝土的抗拉强度越低。 (2)对二级配含畸形骨料配混凝土各模型方案的骨料破碎情况进行了统计分析,结果表明Ck越大、Zb越高、Jp越小时,产生骨料破碎试件的个数越多,同时在统计中发现破坏的骨料均为畸形骨料。 (3)根据各模型方案模拟结果建立的多元线性回归方程,畸形骨料的3个变量(Ck、Zb、Jp)与混凝土抗拉强度之间呈现负相关,且影响权重表现为Ck>Jp>Zb。因此,在混凝土的配制中若中存在针状骨料,建议应首先考虑对针状骨料长宽比的控制,同时应尽量减少在大级配骨料中的针状骨料占比。1.2 本构关系的选取
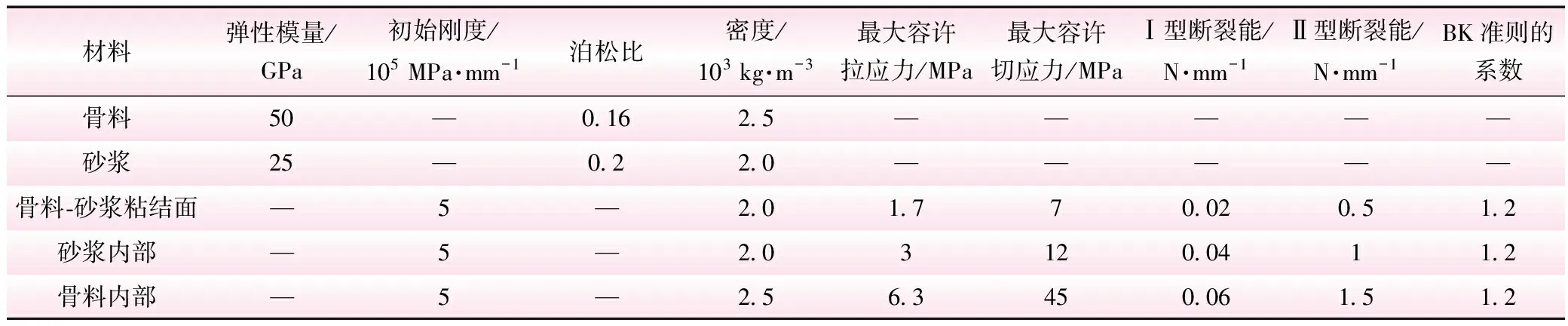

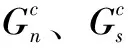
1.3 模型参数校调
2.1 含畸形骨料混凝土模型方案
2.2 抗拉强度结果分析
2.3 单轴受拉全过程分析

2.4 骨料破碎情况分析
2.5 多元线性回归分析
3 结 论
