考虑裂纹闭合影响的岩石变形破坏过程模拟研究

2022-06-22陈文富

水力发电 2022年5期

彭勇，陈文富

(1.中国电建集团贵州电力设计研究院有限责任公司，贵州贵阳 550081；2.贵州鑫达建设工程质量检测有限公司，贵州贵阳 550081)

0 引言

岩石本身具有非均一性、各向异性、非连续性，固其结构特性较为复杂多变，进而导致其多样的变形破坏模式和错综复杂的力学性质。岩石的本构关系涉及到岩石的变形破坏机理，然而目前研究并没有实质性的进展。损伤理论有助于揭示岩石破坏机理，结合损伤理论的本构模型研究也取得了一定的突破，但仍需向全方位发展，而不仅仅是基于小细节上的改动，特别是针对裂纹扩展情况，使其适用于实际岩石工程。

目前，关于岩石损伤本构模型的研究多数从微观角度，假定岩石的微元强度符合某种概率分布函数，进而推导损伤演化关系，基于某种强度准则构建损伤本构模型，此类研究已取得了一定进展[1- 4]。较为常用的几种概率分布函数，包括Weibull分布、正态分布、对数正态分布、幂函数分布和指数函数分布，基于这些分布参数建立的损伤本构模型多数不具备通用性，无法反应不同围压下的试验情况[5]。如Weibull分布函数并不适用于准脆性材料，这是因为准脆性材料具有尺寸效应，若材料是一种准脆性岩石，那么建立损伤本构模型时依托Weibull分布函数就会存在纰漏。此外，正态分布具有两头低、中间高的特征，若使岩石的微元强度服从该分布，可能导致岩石强度参数值出现负数，因此依托正态分布函数构建损伤本构模型也有明显缺陷。基于对数正态分布、幂函数分布和指数函数分布建立的本构模型亦存在较为明显缺陷，未考虑岩体内部初始裂纹，以及岩体变形过程中裂纹逐渐扩展这一动态现象。

本文为建立一种适用范围更广、考虑裂纹扩展情况的损伤本构模型，在现有研究基础上，假设岩石微元强度服从Harris分布函数，并考虑裂纹扩展情况，进而引入裂纹闭合系数，建立考虑Harris分布和裂纹闭合效应的岩石损伤本构模型，提出了Harris分布参数的确定方法，并基于室内试验得出的粉砂岩应力应变数据及参考相关文献的岩石数据对本文模型进行了双重验证。

1 岩石损伤模型的建立

首先，基于J.Lemaitre应变等价理论，构建损伤本构模型，表示如下

[σ*]=[σ]/(1-hD)=[E][ε]/(1-hD)

(1)

式中，[E]为岩石材料弹性矩阵；[σ*]为有效应力矩阵；[σ]为名义应力矩阵；[ε]为应变矩阵；D为岩石的损伤变量；h为裂纹闭合系数，取值范围0≤h≤1。

若岩石破坏前的微元强度表现为线弹性特征，且认定为符合虎克定律，则式(1)可改写为[6-7]

[ε]=[E][σ*]=[E][σ]/(1-hD)

(2)

据文献[8]可知，依托Harris分布函数，该函数具有衰减特性，公式如下

(3)

式中，F为自变量；S为因变量；a、b为大于0的模型参数。

假若将Harris概率分布函数作为岩石微元强度服从的一种准则，只需基于式(3)，求自变量F的导数，即可得出岩石微元强度的概率密度函数，用p(F)表示，即

(4)

将p(F)作为损伤变量D，可得岩石的损伤演化方程为

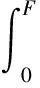
(5)

联立式(4)、(5)可得

(6)

由式(6)可知，由于p(F)>0，损伤演化方程具有单调递增的特性。2种极端情况：当F=0时，D=0，对应没有损失的完整岩石；当F趋向于无穷大时，D=1，对应岩石完全破坏，不再有承载能力。

三轴压缩情况下，只需联立式(2)、(6)，即可获得三轴情况下的损伤统计本构模型，即

(7)

式中，σ1为最大主应力；E为弹性模量；ε1为轴向应变；σ3为围压；μ为泊松比。

由于岩石屈服准则多样性且形式复杂，如若将轴向应力作为微元强度，则不利于岩石损伤模型的建立及求解，其求解形式将十分复杂，推广应用较难；如若将轴向应变作为微元强度，相比较而言，模型表达式更为简易、方便求解。因此，微元强度选取轴向应变，即令F=ε1，则根据式(7)可得岩石损伤本构模型，即

(8)

2 分布参数的确定方法

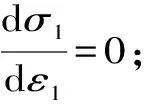
(9)

由条件②可得

(10)

由式(9)、(10)可以求出参数a与b，即

(11)

(12)

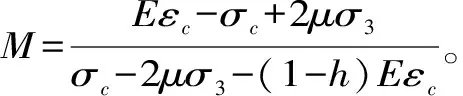
联立式(11)、(12)代入式(8)，构建了考虑裂纹闭合效应的岩石损伤本构模型，该模型包含了Harris分布函数的参数a与b。

3 岩石室内试验

试验材料主要为粉砂岩，试验采用伺服控制岩石三轴压力试验仪器，围压σ3设定为0、5、10、20 MPa。岩石应力-应变曲线见图1。经过观察，岩石破坏形式有共轭剪切、张剪破裂并存、以剪切破坏为主3种。岩石各参数与围压的关系见图2。从图2可知，岩石峰值应力、峰值应变和残余强度均随围压的增加而增大，三者与围压的拟合均呈较好的线性关系。此外，低围压下粉砂岩表现为较强脆性，高围压下表现为较强塑性。高围压下岩样的残余承载能力越强，残余强度与峰值应力之比越来越大。无围压时，比值约为0.17；围压为10 MPa时，比值约为0.44；围压为10 MPa时，比值约为0.63；而围压为20 MPa时，比值约为0.8。

图1 不同围压下的应力-应变关系

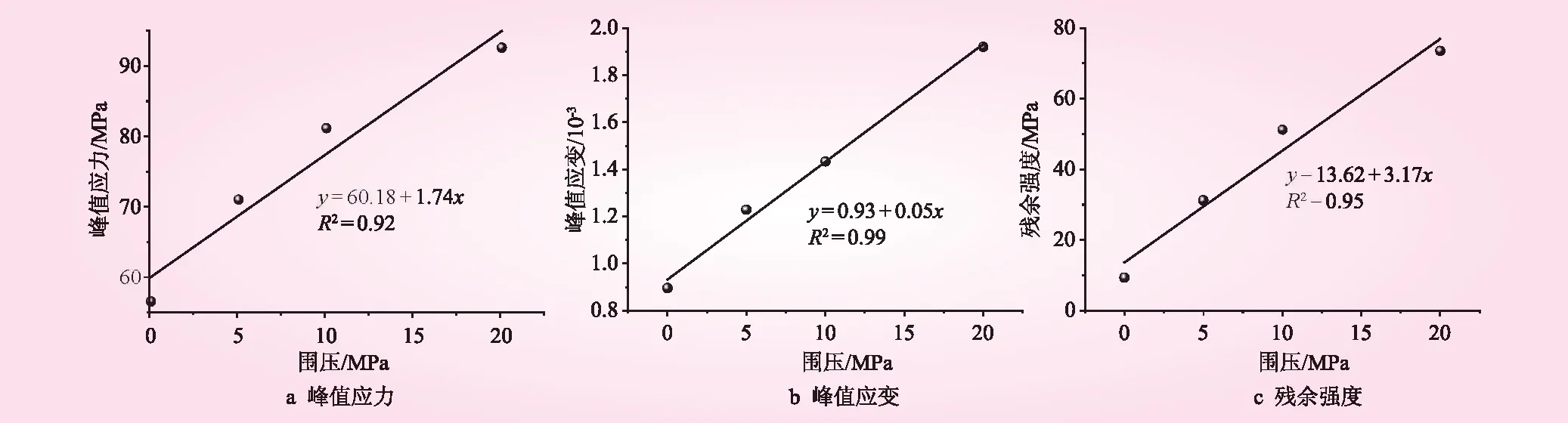
图2 岩石各参数与围压的关系

依据试验曲线获取本文提出模型曲线。图3为粉砂岩的试验曲线与模型曲线对比结果。从图3可知，各围压下的试验曲线与模型曲线吻合度均较好，峰前部分两者相似度更甚，峰后匹配效果较峰前差，预测的残余强度整体高于试验获得的残余强度；此外，本文提出的模型能够一定程度反映峰后的脆延转换特性，表明本文提出的模型适用于描述粉砂岩的变形破坏特征。

4 工程实例与模型的进一步验证

为说明本文提出模型是否适用其他岩性，本文采用参考文献[9]的岩石三轴压缩试验数据，提出试验曲线数据，获取4种围压下的数据对比验证。表1为4种围压下的模型参数。

表1 不同围压下本文模型的参数

裂纹闭合系数值较难确定，本文选定不同的h值，如当h=0.8、0.85、0.9和1时，得出不同裂纹闭合系数下的本构方程。很明显，当h=1时，建立的本构方程即为前人研究的未考虑裂纹闭合效应的岩石损伤本构方程，故本文模型能够选用不同的模型曲线进行拟合。

试验曲线与理论模型曲线比较见图4。从图4可以看出，试验曲线与理论曲线拟合效果较好。特别指出的是，峰前阶段的试验曲线部分与理论曲线部分基本重合，峰后阶段也具有相当的匹配程度，说明本文模型是合理和可行的。基于提出模型获取的应力-应变曲线能够完全呈现峰前岩石的应力-应变关系和一定程度反映峰后的破坏过程曲线，一定程度上也反映了岩石的应变软化特性。h值可有效调节应力-应变曲线，峰值前，h值对曲线影响不大，峰值后影响较为明显。岩石的残余强度随着h的减小而增大，然而当h值更大时，更能反映岩石的脆性特征，h=0.9时，试验曲线与理论曲线的重合度最高。因此，选定不同的h值可以获取更为广泛的损伤本构模型曲线，进而取得更好的模拟效果。

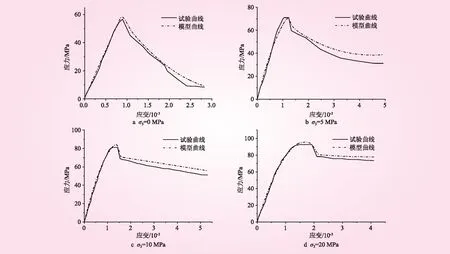
图3 粉砂岩的试验曲线与模型曲线对比

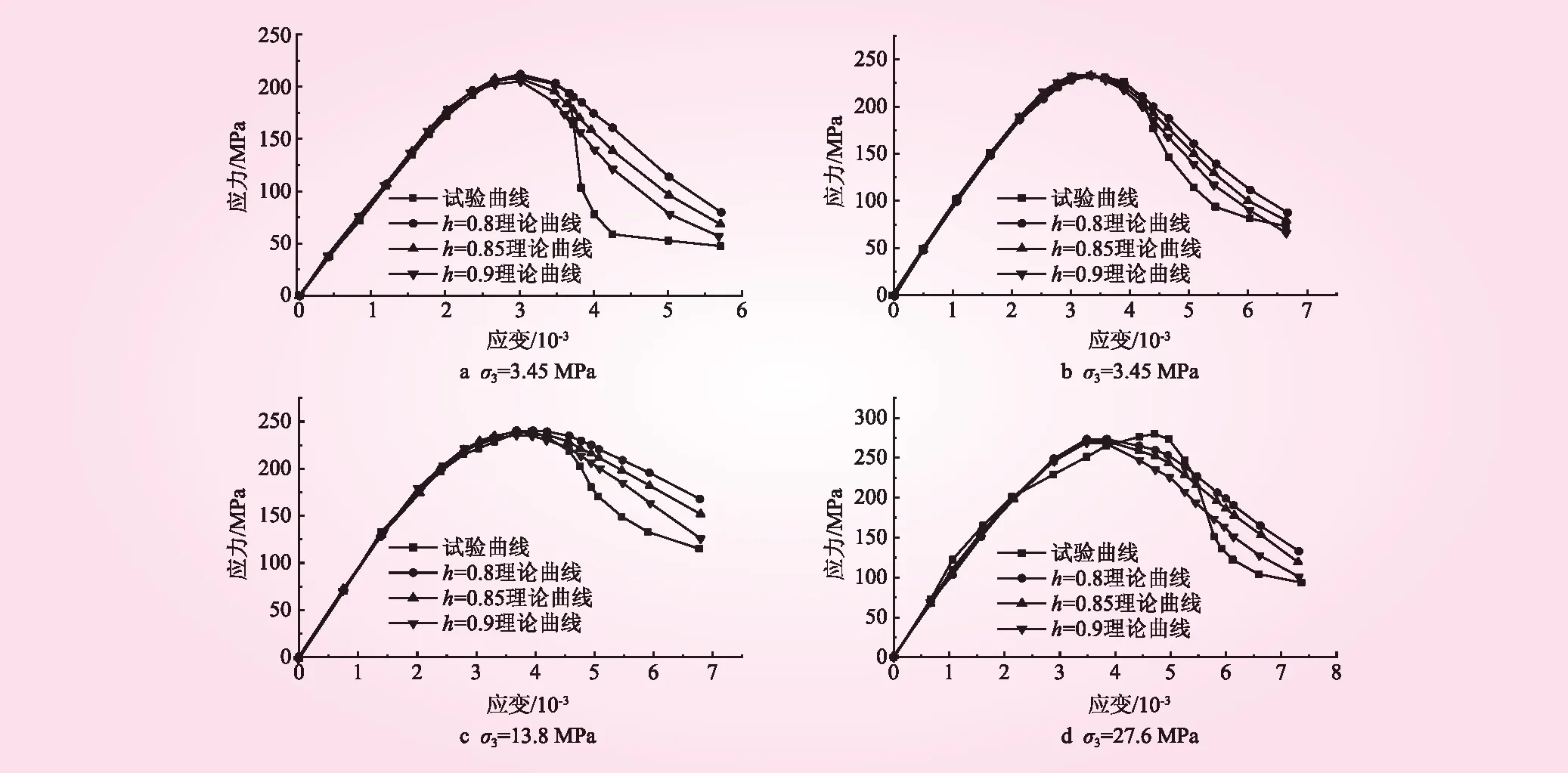
图4 试验曲线与理论曲线的比较

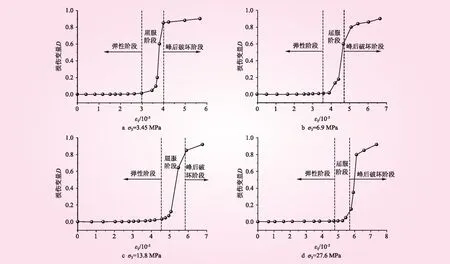
图5 不同围压下的损伤演化曲线

将表1中的Harris分布参数值代入式(6)获取损伤演化曲线，见图5。从图5可以看出，损伤演化曲线大致呈现“S”形，是一个递增的过程。损伤演化曲线初始阶段对应岩石破坏过程的弹性阶段，损伤变量很小，其值近乎为0，曲线趋于水平；曲线中间阶段对应于屈服阶段，该阶段维持时间较短，曲线斜率迅速增加；末端曲线又趋于水平，对应于峰后破坏阶段，曲线斜率迅速降低，曲线趋于水平。