耦合数值降雨信息的径流预报方法对比

牟时宇，朱艳军，杨冬梅，曲 田

(国能大渡河流域水电开发有限公司，四川 成都 610041)

径流预报作为防洪减灾的“参谋”，为梯级水电站的优化调度、风险管控、水资源综合利用提供重要保障。传统的过程驱动径流预报理论，经历了由具有系统理论的黑箱模型到概念性模型再到具有物理成因的分布式水文模型的发展过程[1-2]，期间涌现了斯坦福模型、新安江模型、SHE模型、SWAT模型等经典水文模型。近年来，随着人工智能和数据驱动统计技术的快速发展，数据驱动模型因其开发速度快、易于实时实现、比基于物理基础的水文模型所需信息少等优点，在水文建模和预测、水文规律挖掘中得到广泛应用[3-5]。不论是过程驱动还是数据驱动模型，由于其所考虑的因素、对水文过程概化的方式以及结构组成的不同，均无法普遍适用于复杂的流域水文系统[6]。针对某一特定流域，如何选择最适合的模型结构和模型参数，是水文模拟和径流预报的关键[7]。

基于落地雨的传统水文预报方法，由于流域汇流时间本身的限制，难以完全满足流域防洪调度决策、洪水资源化利用的要求。现代数值天气预报技术的出现，为提前并可靠地预测河川径流提供了重要支撑[8]。耦合数值降雨预报信息的水文预报已成为提高流域来水预报精度和延长预见期的主要途径。大渡河上游属川西高原气候区，植被尚好，属蓄满产流方式。本文以大渡河上游丹巴断面为研究对象，分别应用新安江-融雪径流预报模型、基于预报总误差分析途径的概率预报模型、多因子最近邻抽样回归模型3种径流预报方法，耦合“智能网格”数值天气预报产品，对比不同模型日径流预报效果，优化流域径流预报方案，为梯级水电站精细化调度提供更为丰富的决策支持信息，为其他相似流域的水资源配置、洪水风险管理提供借鉴。

1 模型与方法

1.1 新安江-融雪径流预报耦合模型

新安江(XAJ)模型是以蓄满产流为理论基础的、适用于湿润和半湿润地区的概念性模型。在实际径流模拟中，新安江模型的设计结构通常呈分散性，即将流域划分为一组子流域以捕捉降雨和下垫面的空间异质性。各子流域的径流模拟主要包括蒸散发、产流、分水源、汇流四个部分[9]，其水量平衡可表示为

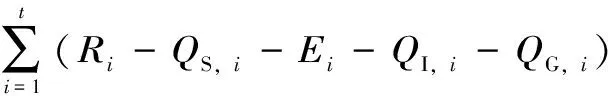
(1)

式中，Wt为流域平均张力水蓄量；St为流域平均自由水蓄量；W0、S0分别为初始张力水、自由水蓄量；R为产流量；E为蒸发量；QS、QI、QG分别为地表径流、壤中流、地下径流。

考虑到大渡河流域上游高山区覆盖有一定面积的积雪，3月～5月河川径流受融雪和冰川补给，引入度-日因子法[10]。在现有新安江模型产流模块中加入融雪径流计算，构建新安江-融雪径流预报耦合模型(XAJ-DDF)。其中，由于气温升高而导致的积雪消融量Mt采用度日因子法计算

Mt=DDF(T-T0)

(2)

式中，DDF为度日因子；T为气温指标，可为日平均气温或日最高(低)气温；T0为基础温度，常取值为0 ℃。

1.2 基于预报总误差分析途径的概率预报模型

基于预报总误差分析途径的概率预报模型分为水文不确定性处理器(HUP)、模型条件处理器(MCP)和误差异分布概率预报模型(EHDA)3种途径。其中，HUP通过分析新安江模型的模拟结果与实测序列的误差，利用贝叶斯理论估计预报变量的后验分布；MCP采用正态分位数转换技术，推求预测变量的分布函数；EHDA首先分析不同量级流量对应的预报误差的异分布性，并在此基础上，采用随机变量函数的概率分布推导方法推求预报变量的条件概率分布，实现径流概率预报[11-12]。

若将Y和M分别记为预报变量的真实值及确定性预报值(新安江模型预报结果)，则预报变量的条件概率分布为

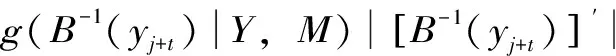
(3)

式中，yj+t为(j+t)时刻的预报变量；mj+t为(j+t)时刻的确定性预报值；g(·)为预报误差的后验分布函数；B为预报变量与预报误差的对应关系。据此流量预报条件分布函数，可获得流量的预报倾向值(50%概率对应的分位点，即中位数)和任一置信水平下的流量预报区间。

1.3 多因子最近邻抽样回归模型

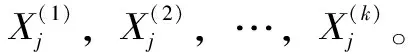
(4)

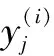
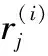
(5)

式中，Xps为降雨特征指标；Xqs为径流特征指标。

1.4 模型评价指标

本研究选取洪峰相对误差、洪峰滞时、径流深相对误差以及Nash效率系数作为预报方案评价指标，Nash效率系数

(6)

式中，Qm，i为模拟/预报流量；Qi为实测流量。

2 模型应用

2.1 研究区域与资料

丹巴是大渡河干流重要水文站，其控制区域降雨集中在6月～9月，多年平均径流量为400～500 mm，其径流的变化情况较大程度上直接反映了河源区的流量变化。本研究选取大渡河丹巴以上流域为研究对象，实测资料来源于流域内日部、一林场、绰斯甲、大金等10个水文站2009年～2020年逐日流量资料序列，以及班玛、阿坝、灯塔等25个雨量站同期逐日降雨资料序列，其站点分布如图1所示。

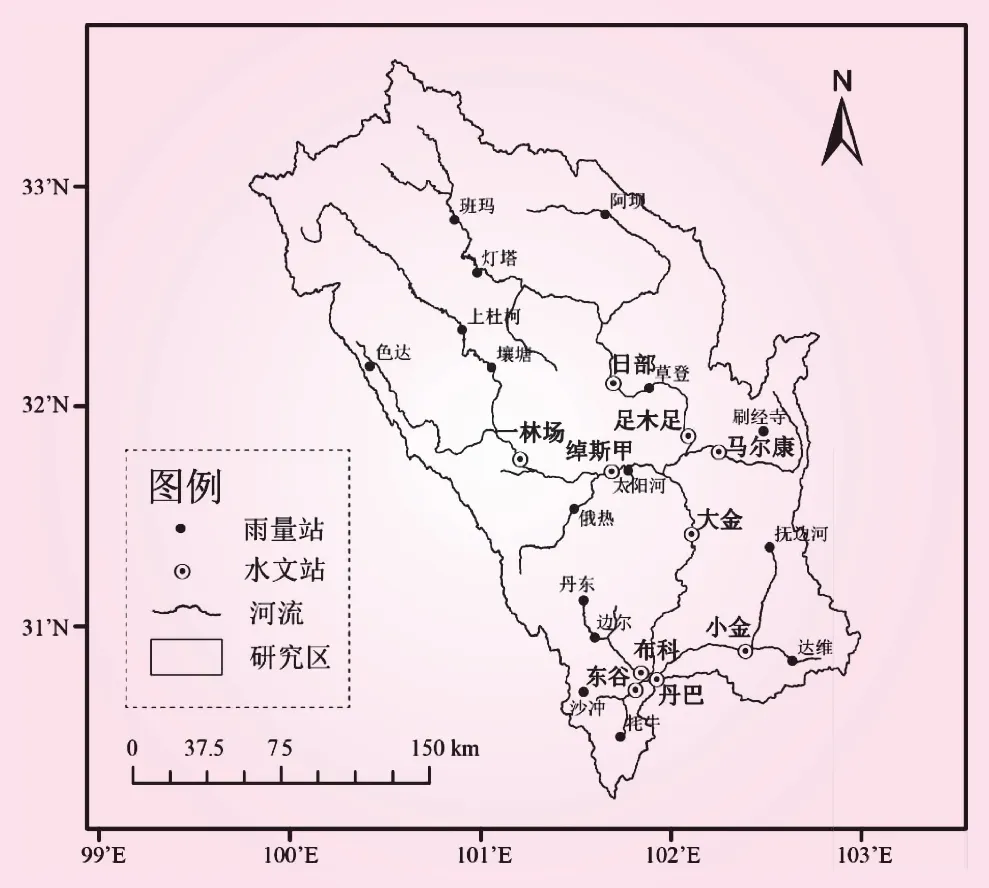
图1 大渡河丹巴以上流域站点分布示意

预报降雨资料来源于“智能网格预报”数值预报产品，是基于我国气象预报服务统一数据源的“一张网”网格预报业务，空间分辨率为5 km×5 km，可实现逐3 h发布未来7 d的天气预报。基于2019年6月～10月实测降雨数据，采用模糊评分、TS评分、预报偏差检验[14]等多种指标综合评估该产品的预报能力，结果表明智能网格预报在流域上游对大雨和暴雨具有较好的预报精度，对中雨以下量级容易出现偏大的情况，总体表现较优，正确率达到91%。通过协-克里金插值获得模型降雨输入，可为径流预报提供稳定、可靠的数值降雨预报信息。

2.2 模型构建

2.2.1 XAJ-DDF模型的率定

考虑到研究区地形、下垫面条件的空间异质性，将丹巴以上流域划分为10个子单元，分别进行产汇流计算；大渡河流域同时具有高山峡谷、草甸、冰雪冻土等多类地形地貌，产汇流机制复杂，降雨和径流量存在明显的季节变化特征，难以用单一结构模型模拟天然径流过程。为此，将全年划分为12月～3月的退水期(考虑融雪)，4月～5月的过渡期(考虑融雪)，6月～8月的夏季汛期和9月～11月的秋季汛期，对不同季节的降雨采用不同参数驱动XAJ-DDF模型以获取出口断面的流量过程，从而提高预报精度。选择2009年～2016年为率定期，2017年～2019年为检验期，运用动态系统微分响应法[15]降低面降雨量(雪水当量)输入的不确定性，以校正模拟的径流过程。率定期和检验期日径流过程的模拟精度见表1。

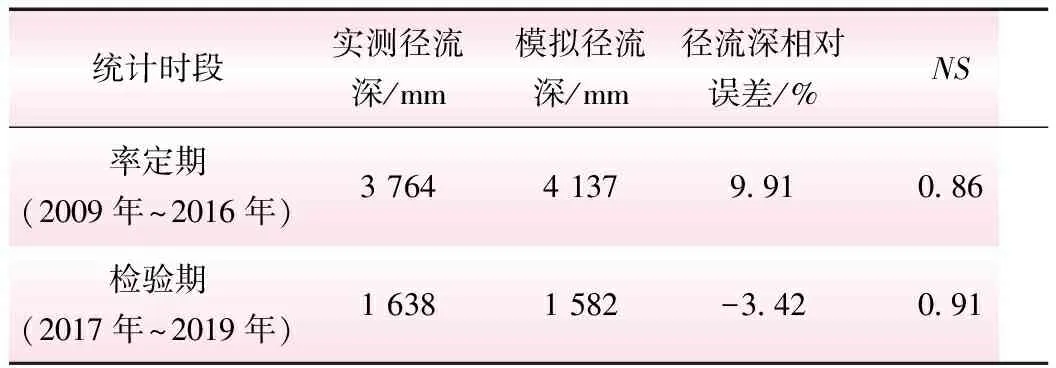
表1 新安江-融雪径流预报耦合模型日径流过程精度统计

结果表明：分季节XAJ-DDF模型在率定期和检验期的径流深相对误差都低于10%，平均NS在0.85以上，在丹巴以上流域具有较好的适用性。

2.2.2 基于预报总误差分析途径的概率预报模型的优选

基于率定期(2009年～2016年)XAJ-DDF模型预报结果，分别采用HUP、MCP和EHDA 3种概率预报模型进行丹巴以上区域径流概率预报。其中，流量的预报推荐值(50%概率对应的分位点，Q50)结果见表2。

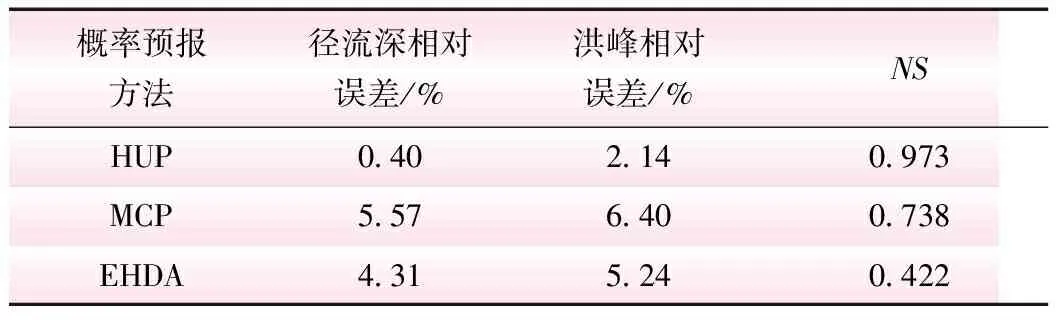
表2 率定期丹巴HUP、MCP、EHDA径流概率预报结果(Q50)

从表2中可以看出，HUP模型预报径流深和洪峰误差均小于3%，确定性系数达到0.973，径流模拟精度高，相比于MCP和EHDA模型，更适合大渡河丹巴以上流域径流概率预报；故，选定HUP模型进行研究区概率预报。

2.2.3 多因子NNBR模型的优选

针对研究区在涨水、退水阶段的产流汇流特性，考虑前期降雨滞时长度的不同，分别构建只考虑前1 d降雨的短降雨滞时模式和考虑3 d降雨的长降雨滞时模式。前者以退水期预报为主，后者以涨水期预报为主，且两种模式可根据前期特征矢量数据进行自适应切换。

根据流域雨量站点分布特征，将其分为5个子区域，以实现输入因子的降维。根据输入因子和输出形式的不同，设计了共10种预报方案，使用2008年～2016年(训练期)的历史数据构建样本集， 2017年～2019年(检验期)不同方案的相似性预报结果如表3所示。

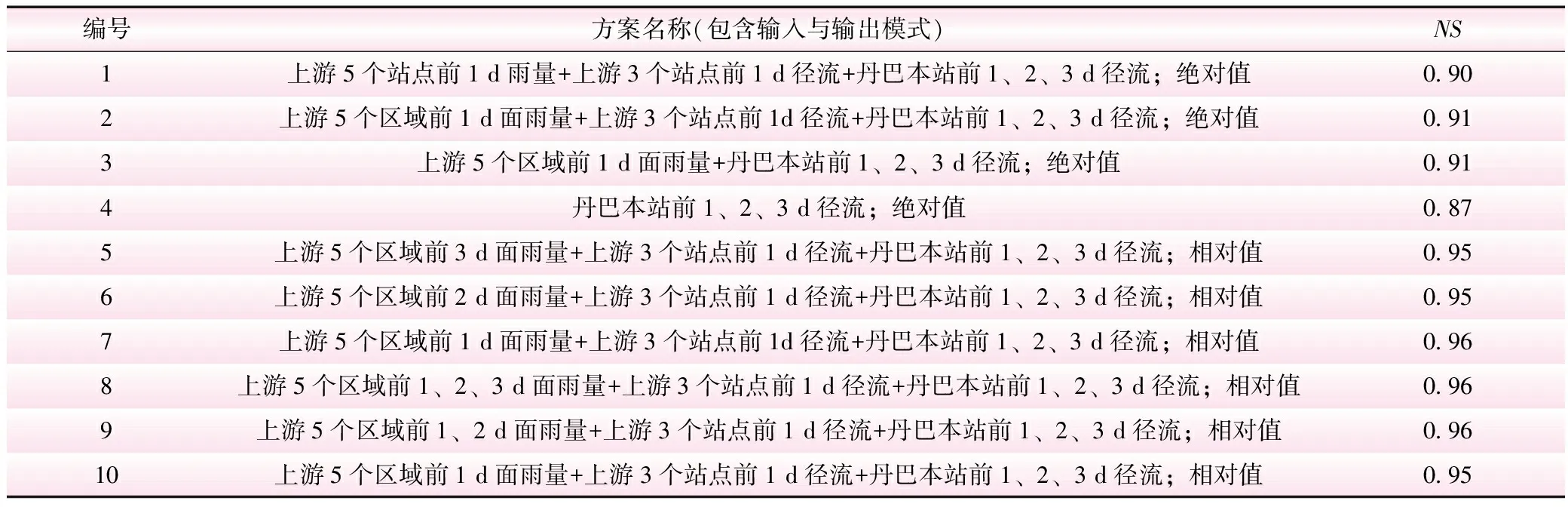
表3 检验期不同预报方案的预报精度评价

结果表明：采用面雨量输入的预报效果优于点雨量输入，采用相对值输出的预报效果优于绝对值输出。方案7～9的NS均为0.96，预报精度最高，进一步采用均方根误差(RMSE)评价3种方案的预报精度，对比可知方案9的RMSE最低，为127.6 m3/s。故，选取方案9作为多因子最近邻抽样回归模型的预报方案。

3 预报结果对比与分析

3.1 汛期预报结果对比

基于2020年5月1日～2020年10月31日逐日滚动更新未来7d的智能网格降水预报数据，检验3种模型的日径流过程滚动预报精度，分别对比3种模型在1、3、7 d预见期下的预报精度，如图2所示，表4给出了不同预见期下的预报精度统计结果。

从图2可以看出，3种模型得到的汛期流量过程与实测资料一致，说明各个模型均能较好地反映研究区的产汇流规律；由表4的统计结果可知，在1、3 d预见期下，3种模型模拟的径流深、洪峰相对误差都小于10%，洪峰滞时小于2 d，NS均在0.8以上；在7 d预见期下，HUP和多因子NNBR模型对径流量预报效果较好，而多因子NNBR受历史样本代表性的局限，对洪峰流量的预报误差较大，容易低估洪水风险。综合径流深相对误差、洪峰相对误差、NS多个指标，HUP模型在汛期表现最优且较为稳定，其提供的预报推荐值Q50的精度整体要优于初始XAJ-DDF模型结果，伴随估计结果的90%置信区间覆盖率较高(92%)，且离散度在0.27以内，可为决策人员明晰洪水风险提供依据。

3.2 枯期预报结果对比

基于2020年11月1日～2021年3月1日逐日滚动更新未来7 d的智能网格降水预报数据，检验3种模型的日径流过程滚动预报精度，分别对比3种模型在1、3、7 d预见期下的预报精度，如图3所示，表5给出了不同预见期下的预报精度统计结果。

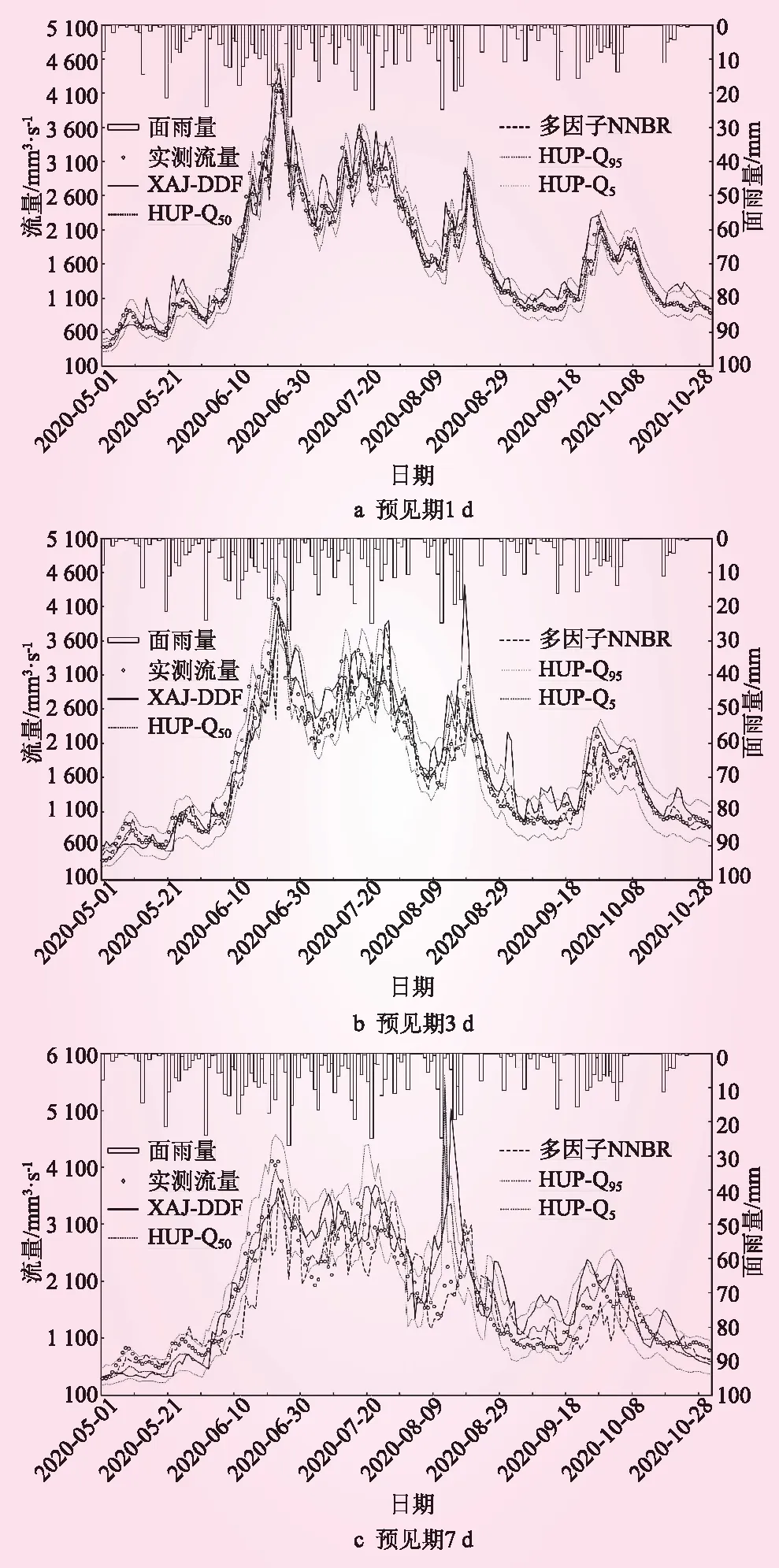
图2 不同预见期下3种预报方法在汛期的径流预报结果

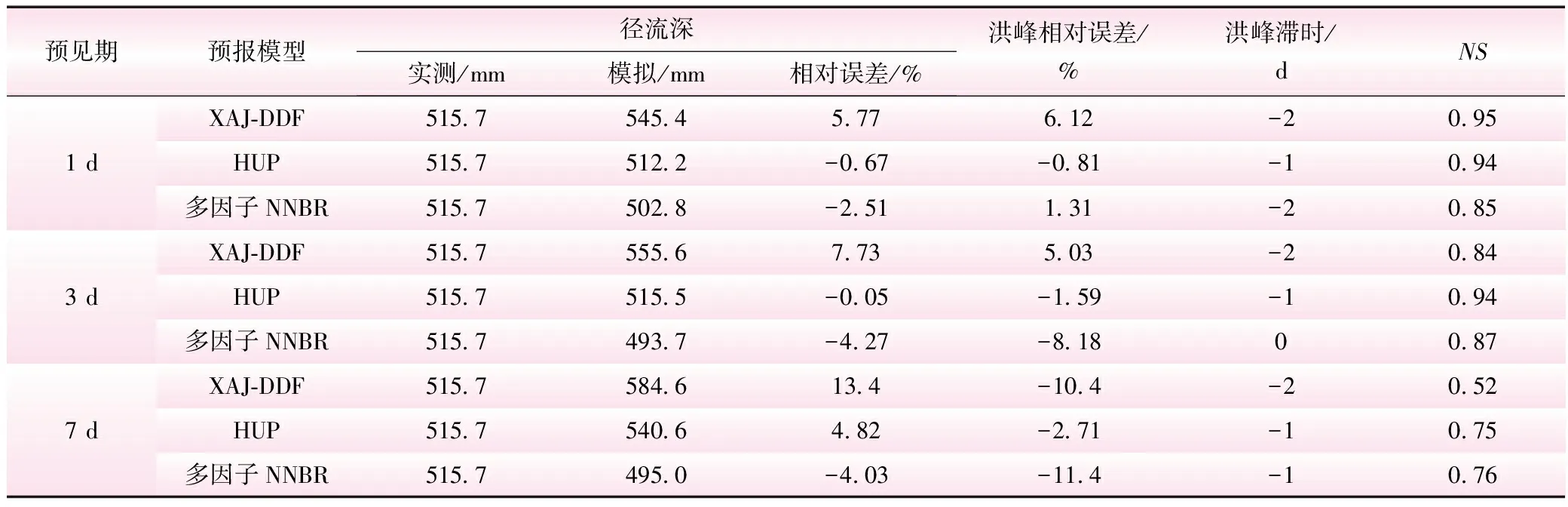
表4 不同预见期下3种预报方法在汛期的预报精度统计

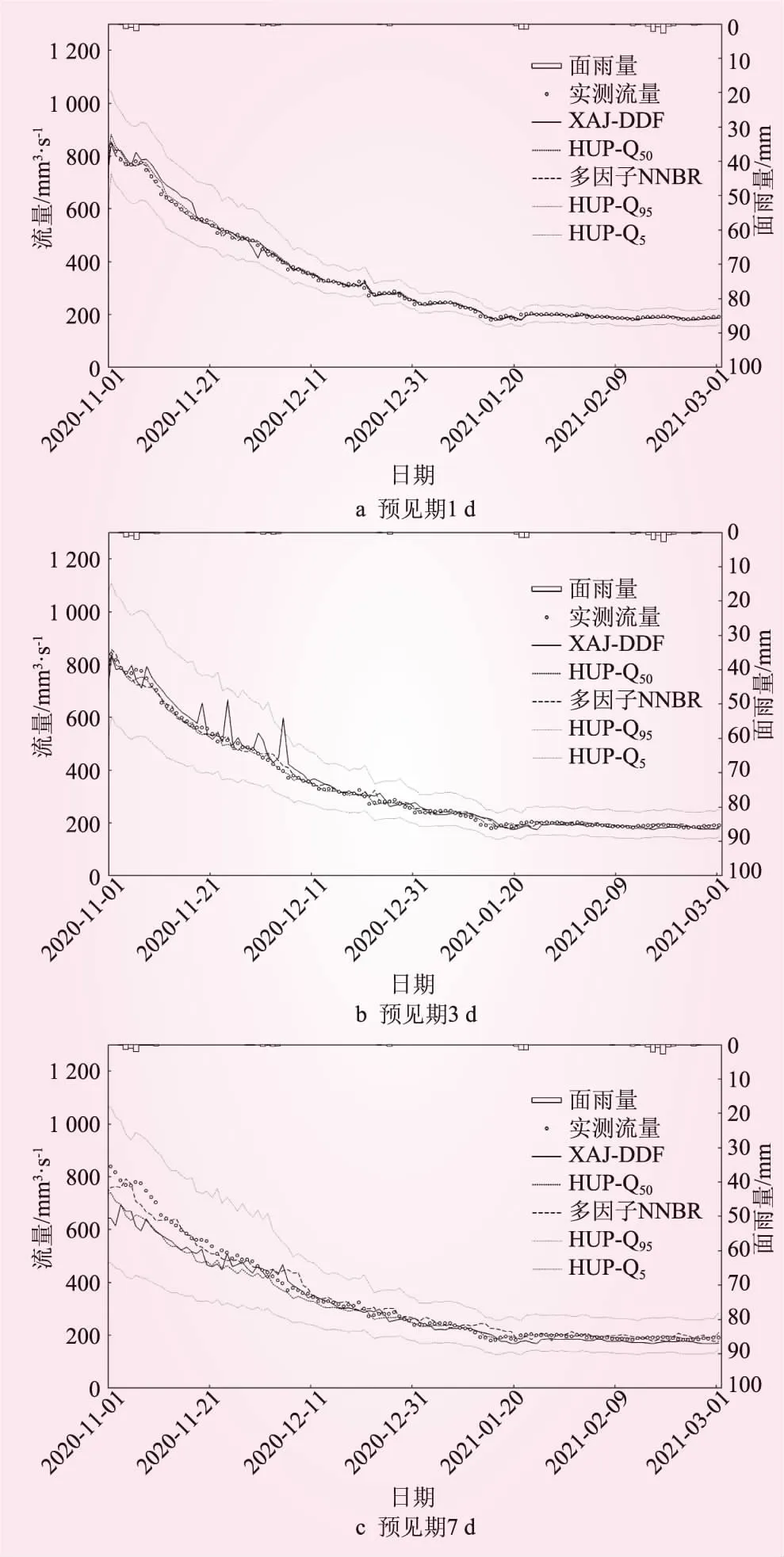
图3 不同预见期下3种预报方法在枯期的径流预报结果

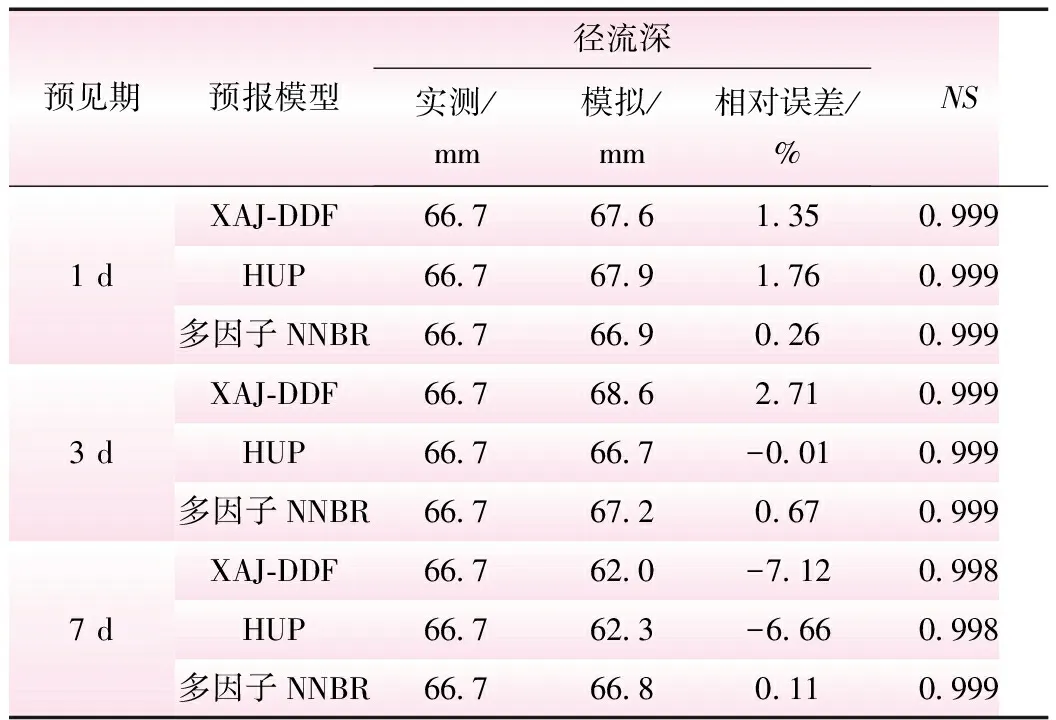
表5 不同预见期下3种预报方法在枯期的预报精度统计

结果表明，3种模型在枯水期的预报精度较好，无论处于何种预见期，径流深相对误差均小于10%，NS接近1。在7 d预见期下，XAJ-DDF和HUP模型在退水初期退水速度偏快，使其预报值偏小。因此，综合径流深相对误差和NS两个指标，多因子NNBR预报精度最高，因其充分挖掘了退水期历史样本的变化规律，对退水期的流量波动把握更准。

4 结 论

以大渡河丹巴以上区域2009年～2019年的实测降雨、径流资料为基础，应用新安江-融雪径流预报模型、基于预报总误差分析途径的概率预报模型、多因子最近邻抽样回归模型3种径流预报方法模拟流域出口断面日径流过程，并引入数值降雨预报信息，分汛期和枯期，分别比较3种模型在1、3、7 d三种预见期下的日径流预报精度。结果表明：

(1) HUP模型在汛期表现最优且较为稳定，其提供的预报推荐值Q50的精度整体要优于初始XAJ-DDF模型结果；而且伴随着估计结果的90%置信水平下的预报区间信息为决策人员明晰洪水风险提供依据。

(2)3种模型在枯水期的预报精度均较好，综合径流深相对误差和NS两个指标，多因子NNBR预报精度最高，对退水特征把握最准。故推荐HUP模型进行丹巴以上流域汛期径流预报，多因子NNBR模型进行枯期径流预报。实际预报中，应依据指定需求动态选择预报方案，必要时可将3种模型的预报结果融合，以提升流域预报水平。