不同边界约束对锚杆锚固段承载特征的影响

李怀珍，贺 炫

（河南理工大学 安全科学与工程学院，河南 焦作 454000）

我国每年新掘进巷道总长达12 000 km[1]，目前巷道围岩主要采用锚杆支护方式[2]，掌握锚杆锚固段承载特征是进行锚固支护设计的基础，也是加强煤层巷道围岩控制和煤矿安全高效生产的前提和保障。因此，许多学者开展了锚杆承载特征相关研究工作。在锚杆承载能力大小计算方面，基于破裂面形状和不同准则推导出锚杆（索）极限抗拔力计算公式，同时研究了锚杆外形参数、锚固剂弹性模量等因素对锚杆锚固性能的影响[3-10]；在界面剪应力分布规律方面，推导出了界面剪应力分布特征及其解析表达式[11-16]；在锚杆承载特征影响因素方面，开展了不同加载方式、动态挠动对载荷传递规律和锚固承载结构稳定性影响研究，取得不少研究成果[17-21]，为巷道锚固支护理论和技术提供了有力支撑。受煤巷围岩条件复杂多变、测点布置和数据测取困难等因素影响，室内张拉试验研究方法被广泛采用。由于研究侧重点和工程背景不同，以往试件轴向加载时边界约束条件可划归以下4 类：第1 类为顶端固定且侧向约束[22-24]；第2 类为顶端被固定侧向不受约束[25-27]；第3 类为底端固定且受侧向约束[28-29]；第4 类为底端固定侧向不受约束[7,19,21,30]。以往研究成果表明，不同边界约束条件下锚杆承载特征差异较大；煤巷支护中的锚杆要经历安装预紧、锚杆-围岩协调变形、采掘挠动等多个锚固支护时段，其承载状态和围岩边界约束条件明显不同。为此，基于煤巷围岩锚杆不同承载状态和围岩边界约束条件开展锚杆承载特征对比研究。

1 煤巷围岩锚固单元体承载状态分析

巷道开挖后须立即进行锚杆锚固支护，巷道围岩锚固支护情况和锚固单元体[31]示意图如图1。

图1 煤巷围岩锚固单元体示意图Fig.1 Schematic diagram of anchoring unit in surrounding rock of coal roadway

以非全长树脂黏结锚固锚杆为例进行锚固单元体承载状态分析。锚杆在张拉预紧时，主要通过锚杆钻机对螺母施加扭矩完成初始安装，锚杆自由段受张拉作用发生变形而产生预紧力。锚杆锚固段借助锚固剂锚固于深部稳定岩层中，锚杆外端通过螺母、垫板和锚网把轴力传递并扩散至浅部围岩表面产生预应力，防止浅部围岩破碎而降低强度，从而保证巷道围岩安全稳定。以巷道顶板锚固围岩为例，对锚固单元体进行受力分析，锚杆张拉预紧时轴向承载，同时锚固单元体承受侧向约束和一定围岩压力。锚固单元体及锚固支护构件受力分析如图2，巷道帮部锚固单元体与此类似。

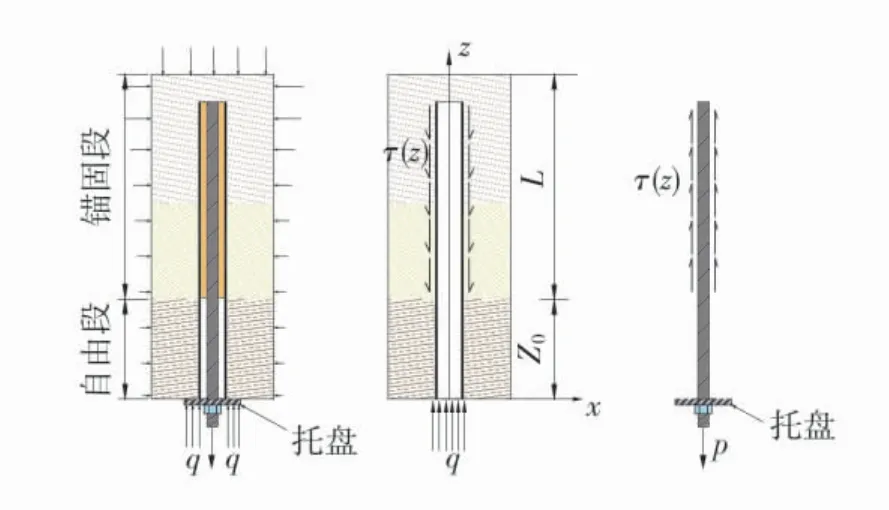
图2 张拉预紧工况顶板锚固单元体受力分析图Fig.2 Stress analysis diagram of roof anchoring unit during bolt tensioning and pre-tensioning

锚杆安装完毕后，随着围岩应力的不断调整，锚杆与围岩发生协调变形，煤帮围岩出现裂纹扩展甚至破碎，顶板产生裂隙甚至离层。由于煤巷浅部围岩破碎变形大于深部，锚网和垫板受浅部围岩变形破坏和扩容作用，通过螺母把力传递给锚杆，即锚杆-围岩协调变形期间锚杆被动轴向承载，锚固单元体由底端和侧面提供反力，取巷道帮部围岩锚固单元体为例进行分析，受力分析如图3。

图3 围岩-锚杆协调变形工况煤帮锚固单元体受力分析图Fig.3 Stress analysis diagrams of coal wall anchoring unit in the period of surrounding rock-bolt coordinated deformation

2 数值模拟方案

1）网格划分。基于巷道围岩锚固单元体锚杆张拉预紧和围岩-锚杆协调变形2 种承载状态分别建模。为简化模型网格，仅取锚杆锚固段的锚固剂、锚杆和围岩进行网格划分。整个模型网格共划分为100 800 个单元，模型几何尺寸、材料分组、网格划分情况如图4。

图4 数值计算模型网格划分Fig.4 Mesh generation of numerical calculation model

2）边界约束设置。数值计算模型边界约束示意图如图5。锚杆在张拉预紧安装时，锚固单元体顶端承受垫板、锚网等约束，虽然数值计算模型仅选取锚固段，同样可视锚固段顶端受固定约束，侧向承受围岩约束及一定围压，数值计算模型边界约束条件如图5（a）。锚杆与围岩协调变形期间，锚杆自由段承受张拉载荷，锚固段为稳定围岩，其侧向同样承受一定围压和侧向约束，锚固底端可视为固定约束，数值计算模型边界约束条件如图5（c）。为开展对比分析研究，同时构建顶端固定无侧向约束、底端固定无侧向约束数值计算模型，如图5（b）和图5（d）。

图5 数值计算模型边界约束示意图Fig.5 Diagrams of numerical calculation model

3）参数设定。对以上4 种边界约束数值模型进行轴向加载数值计算，载荷大小取60、90、120 kN 3个等级，经过多次调试，设置30 000 时步为收敛条件停止数值运算，此时最大不平衡力低于10 N，相对于张拉载荷不足1/10 000。数值计算中主要参数赋值见表1。

表1 数值计算参数列表Table 1 Numerical calculation parameters list

3 不同边界约束对锚杆轴力分布规律的影响

同边界约束条件下锚杆轴力分布曲线如图6，相同载荷不同边界约束条件下锚杆轴力分布曲线如图7。

图6 不同边界约束条件下锚杆轴力分布曲线Fig.6 Distribution curves of axial force of bolt with different boundary constraints

图7 相同载荷不同边界约束条件下锚杆轴力分布曲线Fig.7 Axial force distribution curves of bolt under the same load and different boundary constraints

由图6 可知，同一边界约束条件下，虽然载荷等级不同，但锚杆轴力沿锚固长度方向分布规律相对一致且均为单调递减，锚杆轴力最大值位于锚固始端，由此可知煤巷围岩支护中的锚杆在锚固外端最容易被拉断；同时，不同边界约束条件下锚杆轴力沿锚固长度方向递减规律不尽相同。顶端固定侧向约束条件下锚杆轴力呈幂函数快速递减，在1/2 锚固深度时轴力递减明显变缓且数值接近0，如图6（a）；顶端固定无侧向约束边界条件下锚杆轴力在锚固外端3 cm 内递减较慢，随后接近单条线性递减，如图6（b）；底端固定侧向约束锚杆轴力在锚固初始端5 cm 内递减缓慢，随后沿锚固长度呈幂函数递减，如图6（c）；底端固定无侧向约束锚杆轴力沿锚固长度开始几乎呈线性递减，在锚固底端10 cm 内递减迅速，如图6（d）；基于前文对煤巷围岩锚固单元体承载状态分析和图6（a）和图6（c）可知，锚杆在预紧安装时轴力沿锚固长度呈幂函数快速递减，锚杆-围岩协调变形期间锚杆轴力在锚固起始段5 cm 范围内轴力递减较缓，随后呈幂函数快速递减。因此，张拉预紧力在达到围岩表面预应力要求后不能过大，同时也可以考虑锚固始端增粗的变直径锚杆。

由图7 可知，顶端固定有侧向约束条件下，锚杆轴力衰减最快，其次为底端固定侧向约束锚杆轴力衰减较快，说明侧向约束对锚杆轴力衰减影响较大。顶端固定无侧向约束边界条件下，锚杆轴力呈线性缓慢衰减，锚固段尾端锚杆轴力较小。底端固定无侧向约束条件下，锚杆轴力衰减最慢，但在锚固段尾部呈快速递减趋势，锚杆底端轴力不接近0 且数值较大。由此可知，当巷道埋深大或围岩应力较大情况下可视锚固段施加了较高围压的侧向约束，一定程度会降低有效锚固长度。

4 不同边界约束对界面剪应力分布规律的影响

4.1 锚杆-锚固剂界面剪应力分布规律

锚固段锚杆和锚固剂的剪应力分布云图如图8，锚杆-锚固剂界面剪应力沿锚固长度分布曲线如图9，相同载荷不同边界约束条件下锚杆-锚固剂界面剪应力分布曲线如图10。

图8 锚固段锚杆和锚固剂的剪应力分布云图Fig.8 Shear stress distribution of anchoring agent and bolt

图9 锚杆-锚固剂界面剪应力沿锚固长度分布曲线Fig.9 Distribution curves of interfacial shear stress between bolt and anchorage agent

图10 相同载荷不同边界约束条件下锚杆-锚固剂界面剪应力分布曲线Fig.10 Distribution curves of interfacial shear stress under the same load and different boundary constraints

由图8 可知，在锚固起始段，锚杆杆体表面和锚固剂环厚内侧均出现剪应力集中现象，并且剪应力集中部位主要分布在距外端口2 cm 处，锚杆杆体剪应力与锚固剂内侧剪应力集中部位可以相互验证。

由图9 可知，相同边界约束条件下不同载荷等级锚杆-锚固剂界面剪应力分布规律基本相同，不同边界约束条件下锚杆-锚固剂界面剪应力分布规律差异较大。顶端固定侧向约束条件下锚杆-锚固剂界面剪应力在距离锚固外端口2 cm 处出现峰值，顶端固定无侧向约束条件下剪应力峰值出现在5 cm 处，底端固定侧向约束条件下，界面剪应力峰值在轴向载荷为60 kN 和90 kN 时出现在距离锚固外端9 cm 处，载荷增加至120 kN 时则出现在距离锚固外端10 cm 处，即随锚杆轴向载荷增加峰值内移。底端固定无侧向约束条件下，界面剪应力在锚固深度35 cm 以内数值不大且相对稳定，在锚固底部10 cm 范围内出现应力集中，在锚杆轴向载荷为60 kN和90 kN 时剪应力峰值出现在距离底端3 cm 处，载荷增加至120 kN 时则出现在锚孔最底端。

由图10 可知，不同边界约束对锚杆-锚固剂界面剪应力分布影响显著，曲线形状截然不同，随着载荷的增加各曲线峰值均呈递增趋势，但分布规律基本相同。顶端固定侧向约束条件下为单峰曲线，峰值靠近锚固起始端，峰值最大接近24 MPa，峰值后剪应力呈幂函数衰减。顶端固定无侧向约束条件下，曲线为单峰曲线，峰值距锚固外端5 cm，峰值大小11 MPa。底端固定侧向约束条件下，剪应力分布曲线为单峰曲线，峰值距锚固外端10 cm，峰值大小接近11.5 MPa。底端固定无侧向约束条件下，剪应力在锚固底端口附近出现最大值，峰值大小达19.75 MPa。

4.2 第1 界面与第2 界面剪应力对比分析

锚固单元体为“三体两面”结构，“三体”分别指围岩、锚固剂和锚杆，“两面”分别指锚杆-锚固剂界面和围岩-锚固剂界面（下文分别简称第1 界面和第2 界面）。绘制了轴向载荷为90 kN 的第1 和第2界面剪应力分布规律对比图如图11。

图11 第1 和第2 界面剪应力分布规律对比图（p=90 kN）Fig.11 Comparison of shear stress at the first and second interfaces（p=90 kN）

由图11 可知，顶端固定有、无侧向约束2 种条件下第2 界面剪应力分布规律基本相同，底端固定有、无侧向约束2 种边界条件下第2 界面剪应力分布规律与顶端固定明显不同。另外，底端固定侧向约束边界条件下第1、第2 两界面剪应力分布规律基本一致外，其他3 种边界约束方式第1、第2 界面剪应力分布规律明显不同。顶端固定时无论有没有侧向约束，第1 界面剪应力均在锚固外端口附近出现剪应力集中，且无侧向约束时剪应力峰值位置更远离锚固外端口，第2 界面剪应力在锚固外端口即出现峰值。顶端固定有侧向约束时，2 个剪应力峰值均较大，底端固定侧向约束时两界面峰值较小且第2界面剪应力峰值小于第1 界面剪应力峰值，说明锚杆-围岩协调变形时段，如果两界面抗剪强度相同条件下第1 界面更容易发生滑移脱黏。由于工程现场受围岩性质、锚杆外形参数、钻孔施工质量、锚固剂材质性能等因素影响，2 个界面抗剪强度不一，因此，锚固支护在张拉预紧、锚杆-围岩协调变形等不同时段发生锚杆锚固失效的模式不尽相同。

结合以上分析可知，由于边界约束条件不同，锚固单元体第1、第2 2 个界面剪应力分布规律、峰值大小和位置明显不同相同，所以，以不同边界约束条件得到的2 个界面剪应力分布存在较大差异。同时，受多种因素影响，第1 和第2 2 个界面的抗剪强度不一样，以致在锚固支护不同时段发生的锚杆锚固失效模式和类型多种多样，需要结合工程地质条件和施工工艺进行综合分析。

5 结 论

1）煤巷围岩锚固支护体系中，非全长黏结锚杆前期经历的张拉预紧承载和锚杆-围岩协调变形承载2 种状态，可分别对应顶端固定侧向约束锚固单元体、底端固定侧向约束锚固单元体中的锚杆轴向张拉状态。

2）不同边界约束条件下，锚固单元体锚杆轴力沿锚固长度方向均呈递减规律分布。顶端固定侧向约束条件下锚杆轴力呈幂函数快速递减，在锚固长度1/2 时轴力递减明显变缓且数值接近0。底端固定侧向约束锚杆轴力在锚固初始端5 cm 内递减缓慢，随后沿锚固长度呈幂函数递减。无论顶端固定还是底端固定，有侧向约束条件下锚杆轴力衰减速度较无侧向约束条件下轴力衰减迅速。

3）不同边界约束条件下第1 界面剪应力分布规律明显不同。顶端固定有侧向约束条件下第一界面剪应力峰值大于底端固定有侧向约束边界条件对应值，顶端固定侧向约束条件下第1 界面剪应力在锚固外端口2 cm 处出现峰值，底端固定侧向约束条件下第1 界面剪应力峰值位于距锚固外端9～10 cm处，随锚杆轴向载荷增加峰值呈内移趋势。

4）不同边界约束条件下第2 界面剪应力分布曲线差异明显。顶端固定有侧向约束条件下第2 界面剪应力峰值位于锚孔外端口，底端固定侧向约束条件下第2 界面剪应力峰值位于距锚固外端口8 cm处，其峰值低于第1 界面剪应力峰值。

5）相同边界约束条件下，锚固单元体第1、第2界面剪应力分布曲线形态各异，其峰值大小和位置也不尽相同。同时，受多种因素影响2 个界面抗剪强度不同，以致锚固支护不同时段发生的锚杆锚固失效模式具备多样性。