基于非平稳随机场的水泥土堤坝边坡可靠度分析

杨亮 刘辉 章荣军 郑俊杰

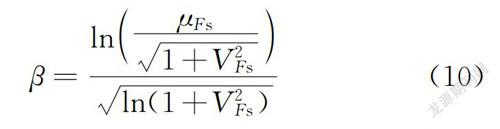
摘 要：采用水泥固化疏浚淤泥作為堤坝填料往往会使堤坝土体参数具有较高的变异性;同时，在水泥土堤坝填筑过程中，通常设置水平排水板加速土体排水固结，这使得主固结完成后水泥土强度随排水板位置呈现一定空间变化趋势，通常的平稳或准平稳随机场模型很难表征这一趋势。为此，提出一种不排水抗剪强度垂直排水板方向衰减的非平稳随机场模型，并以水泥土堤坝边坡为例，结合强度折减法和蒙特卡洛模拟，对比提出的非平稳随机场模型和传统平稳随机场模型、深度趋势非平稳随机场模型对边坡安全系数和滑动面分布的影响，讨论模型中趋势参数对可靠度的影响。结果表明：平稳随机场模型及深度趋势非平稳随机场模型的计算结果偏于危险，提出的非平稳随机场模型既能考虑土体不排水抗剪强度沿深度方向的趋势项与随机波动项，又能考虑其沿垂直排水板方向的衰减趋势，与现有研究符合较好。

关键词：非平稳随机场;水泥土边坡;可靠度分析;不排水抗剪强度;堤坝

中图分类号：TU457 文献标志码：A 文章编号：2096-6717（2022）05-0078-09

收稿日期：2021-07-05

基金项目：国家自然科学基金（51978303）

作者简介：杨亮（1998- ），男，主要从事岩土工程研究，E-mail：yangliang0815@hust.edu.cn。

章荣军（通信作者），男，教授，博士生导师，E-mail：ce_zhangrj@hust.edu.cn。

Received：2021-07-05

Foundation items：National Natural Science Foundation of China （No. 51978303）

Author brief：YANG Liang （1998- ）， main research interests： geotechnical engineering， E-mail： yangliang0815@hust.edu.cn.

ZHANG Rongjun （corresponding author）， professor， doctorial supervisor， E-mail： ce_zhangrj@hust.edu.cn.

Reliability analysis of embankment slope in cement-mixed soil with non-stationary random field

YANG Liang， LIU Hui， ZHANG Rongjun， ZHENG Junjie

（Institute of Geotechnical and Underground Engineering， Huazhong University of Science and Technology， Wuhan 400074， P. R. China）

Abstract：The soil properties of embankment slope filled with cement solidified dredged sludge commonly feature high variability. Meanwhile， in construction process of cement-mixed embankment， horizontal drainage plate is generally used to accelerate the consolidation of cement-mixed soil， which makes the soil strength show a spatial distribution trend at the vertical direction （perpendicular to the drainage plate） after the primary consolidation finished. The traditional stationary or quasi-stationary random field model cannot well characterize this trend. This paper proposes a non-stationary model to characterize the attenuation trend of soil strength along the normal direction of drainage plate. The strength reduction method and Monte Carlo simulation are combined to evaluate the reliability of slope， and the proposed model is compared with two existing models （i.e.， traditional stationary random field model and depth trend non-stationary random model）. The influence of different random filed models on safety factor and slip surface are investigated， and the impact of trend parameters in the proposed model on slope reliability are discussed. The results show that the stationary random field model and depth trend non-stationary random field model may overestimate the reliability of embankment slope， and the proposed non-stationary random field model can consider both the trend term and random fluctuation term in vertical direction and the attenuation trend in normal direction of drainage plate， which is in good agreement with the existing research.

Keywords：non-stationary random field; cement-mixed soil slope; reliability analysis; undrained shear strength; embankment

为了处置大量的河湖疏浚淤泥，一种理想的做法是采用水泥固化高含水率泥浆，再结合真空预压、堆载预压等多种方式将水泥土作为工程（如堤坝）填料，但由于疏浚淤泥杂质众多、施工过程中搅拌不匀、养护条件不一等多种因素，疏浚淤泥固化处理后形成的水泥土堤坝边坡材料参数分布存在较大变异性。

在固化淤泥堤坝填筑过程中，常采用真空预压加速土体固结，需要在堤坝土体内铺设多层水平排水板，针对这种条件下堤坝土体内抗剪强度的分布规律，学者们已开展相关试验研究。周洋等通过试验发现，仅铺设水平排水板时，垂直于水平排水板方向，距离越远土体含水率越高，并且从土体含水率分布情况来看，仅铺设水平排水板的效果要优于仅铺设竖向排水板的效果;张文彬等发现，随着离排水板距离的增加，土体的十字板抗剪强度逐渐减小;高会强发现，铺设水平排水板时，加固后土体表层和靠近排水板的土体强度较高，而远离排水板的土体强度很低，铺设竖向排水板时，随着深度的增加，十字板抗剪强度呈线性增加趋势。根据已有的试验结果可知，在堤坝内铺设水平排水板会使土体的强度特性分布受到影响，且一般的规律是：在一定范围内，距离排水板越远，含水率越高，土体强度越低。

为了描述土体参数的空间分布变异性并进行可靠度分析，常采用平稳随机场模型。所谓平稳随机场即认为土体参数的均值、标准差等统计特征沿埋深保持不变，参数之间的空间相关性只与两点之间的相对距离相关而与其绝对距离无关。这种模型很难表征排水板固结带来的土体强度空间变化趋势。相对于平稳随机场，也有学者提出了非平稳随机场分析模型，在非平稳随机场的表征过程中，土体参数离散变量一般可视为趋势项、残余项与波动分量的多项式，以此表征土体参数在水平方向上的波动性和埋深方向上的趋势性，许多学者展开了相关研究，提出了非平稳随机场的表征方法与趋势项及残余项的处理方法。蒋水华等综合分析了两种非平稳随机场模型的特征：1）采取去趋势分析方法，将土体参数模拟为某一平稳随机场，再基于该平稳随机场，进一步考虑土体参数随埋深的变化趋势分量的影响，从而实现对土体参数二维非平稳随机场的表征，该方法所得非平稳随机场的均值与标准差均随埋深而变化，但其变异系数保持不变;2）取趋势项为趋势分量与土体重度和埋深的乘积，残余项为地表处土体参数值，继而将趋势分量参数模拟为服从某一分布的平稳随机场，忽略残余项的不确定性，得到二维非平稳随机场，该方法所得土体参数的均值、标准差与变异系数均随埋深而变化;在此基础上，Li等提出了一种新的二维非平稳随机场表征方法，验证了所提方法的可行性，系统比较了所提方法与现有二维非平稳随机场与随机场的区别，该方法的优势在于能够同时考虑趋势分量与波动分量的不确定性。豆红强等通过去趋势分析方法，将饱和渗透系数均值视为随埋深递减的线性函数，残余项为地表处平均饱和渗透系数，趋势分量为饱和渗透系数随埋深的变化梯度，建立了表征土体饱和渗透系数变异性的一维非平稳随机场模型，并探讨了土体饱和渗透系数的空间变异性对边坡可靠度的影响。Li等通过不排水抗剪强度、有效竖向应力和黏土超固结比（OCR）之间的经验关系，研究了不排水剪切强度随埋深的变化趋势，在此基础上得到了趋势项随埋深变化的二维非平稳随机场。Shu等取残余项为泥水分界线处的不排水剪切强度，取趋势项为埋深的线性函数，且趋势项与残余项满足对数正态分布，建立了不排水剪切强度的二维非平稳随机场，讨论了自相关距离对深海基础平均承载力与破坏机理的影响;Wu等取趋势项为地表处非零且随埋深线性变化的不排水剪切强度均值，保持变异系数不变，通过高斯平稳随机场的转换与映射，得到了不排水剪切强度的二维非平稳随机场表征，研究了变异系数、分布函数、垂直自相关距离等因素对土体承载力的影响。

基于上述垂直排水板方向强度衰减的一般规律及非平稳随机场相关理论，笔者提出一种水泥土堤坝内垂直排水板方向的不排水抗剪强度随距离衰减的非平稳随机场模型，该模型既能表征土体抗剪强度沿埋深方向增加的趋势，又能考虑垂直排水板方向的强度衰减。在此基础上，给出土体参数三维非平稳随机场模拟计算方法流程，并分析了土体参数非平稳分布特征对边坡可靠度的影响。

1 不排水抗剪强度非平稳随机场模型

1.1 深度趋势随机场

土体参数的空间变异性一般由趋势项和随机波动项联合表征。以无侧限抗压强度随机场为例，试验值q沿深度方向的不平穩特征可表示为

q（h）=t（h）+ω（1）

式中：h为土体埋深;t（h）为与埋深有关的趋势项，一般取相应深度下土体参数的均值;ω为随机波动项，用来描述土体空间内土体参数大小无趋势的随机波动特征，其均值和标准差与埋深无关。通常，土体的无侧限抗压强度随深度增加而增加。简单起见，用线性函数描述土体无侧限抗压强度随深度的变化关系，即

q=q+b·σ′=q+γ·h·b（2）

式中：q为地表土体的无侧限抗压强度（地表UCT试验值）;b为无侧限抗压强度随埋深增加的速率;σ′=γh，为竖向有效应力，γ为土体重度。参考文献[10]的做法，采用去趋势分析方法，首先用一均值为μ、标准差为σ的对数正态平稳随机场模拟q，再在此基础上叠加一个沿埋深线性增加的趋势分量，最终得到三维深度趋势非平稳随机场

q=q（x，y，z）+γ·h·b（3）

1.2 垂直排水板不排水抗剪强度衰减非平稳随机场模型 基于已有的试验研究，可假设土体在排水固结后，抗剪强度与其离排水板的距离线性相关，此时土体随机场可表示为

q（x，y，z）

=q+γ·h·b-d（x，z）·b·exp[ω（x，y，z）]（4）

式中：q、b的含义同前所述，只是此处q为均值，为μ、标准差为σ的随机变量;d（x，z）为土体空间内一点与排水板的垂直距离（排水板沿y方向铺设）;b为垂直排水板方向的趋势项;exp[ω（x，y，z）]为随机波动项。

如图1所示，P为三维空间中截取的某一x-z平面内一点，因排水板（铺设）方向平行于y轴方向，故点P垂直排水板距离d（指距离最近的排水板）只与点P的x、z坐标有关，而与x-z平面所处的位置（y坐标）无关，表示为d（x，z）。

2 算例分析

2.1 算例描述

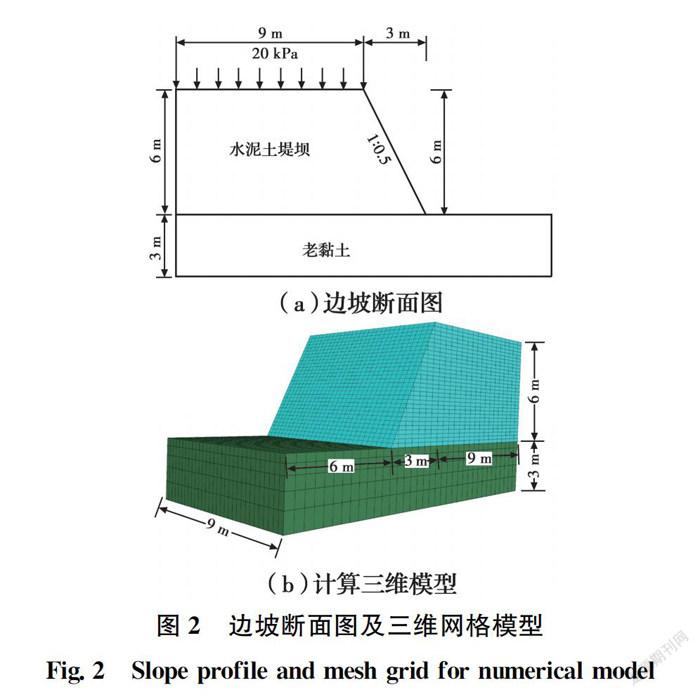
算例为一高陡水泥土堤坝边坡，斜坡高度6 m，坡度1∶0.5，堤坝顶面宽度为18 m，堤坝顶面作用20 kPa的交通荷载（假设为均匀分布）。为了提高计算效率，取半结构进行建模分析，模型断面图和三维网格图如图2所示。

2.2 材料参数取值

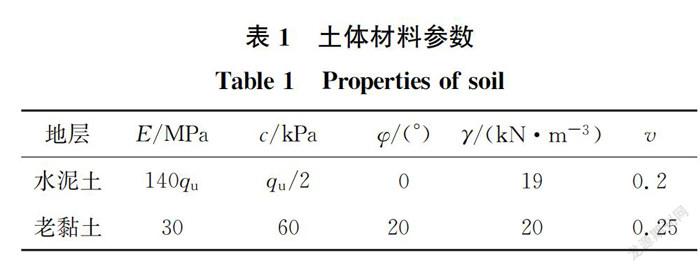
参照Zhang等、Lee等的研究，认为水泥土堤坝边坡无侧限抗压强度服从对数正态分布，固化淤泥形成的水泥土模量E与无侧限抗压强度q呈正比关系，E/q=135～140。考虑到固化淤泥形成的水泥土材料渗透系数很低，参考Liu等的做法，假定主固结完成后水泥土堤坝为完全不排水条件，采用内摩擦角为0的Mohr-Coulomb模型来模拟固化淤泥形成的水泥土，取不排水抗剪强度c=q/2、E/q=140。相应地，堤坝地基土体为老黏土，相关材料参数见表1。

为了探究垂直排水板衰减非平稳随机场模型的可行性，采用3种随机场模型模拟水泥土堤坝部分对比计算结果，下部老黏土采用一般的平稳随机场模型。

模型1为平稳随机场模型，采用地表处的UCT试验均值μ=86 kPa，不考虑其趋势变化，UCT试验值空间随机场采用对数正态分布，变异系数COV=0.3。采用高斯型自相关函数，三维空间内水平、竖向相关距离分别取为38、3.8 m。

模型2为深度趋势随机场模型，三维空间随机场生成公式为

q（x，y，z）=q（x，y，z）+γ·（6-z）·b（5）

式中：q（x，y，z）为对数正态分布的平稳随机场，离散取值同上。土体趋势分量参数b随深度变化，参照蒋水华的统计结果，取b=0.2，为定值。不排水抗剪强度的均值和标准差分别为

μ（h）=μ+γhb

σ（h）=σ（6）

模型3为垂直排水板衰减非平稳随机场模型，在模型计算时，认为排水板附近土体的抗剪强度不断减小。同时，采用静力计算，不考虑排水带来的渗透固结作用，也不考虑排水板自身对土体强度分布的影响。此时，三维空间随机场生成模型为

q（x，y，z）=q+γ·（6-z）·b-

d（x，z）·b·exp[w（x，y，z）]（7）

式中：q为对数正态分布的随机变量，μ=86 kPa，变异系数COV=0.3;趋势参数b=0.2，为定值;b为因真空预压排水固结导致的q随距排水板距离衰减趋势项（排水板處最大），理论上与施工条件有关，参考b的取值结果，考虑其随机性，取b为对数正态分布的随机变量，均值μ=2.0，变异系数COV=0.3;exp[w（x，y，z）]为随机波动项，w（x，y，z）取为均值μ=0、标准差σ=0.3的正态分布随机场，水平、竖向相关距离分别取38、3.8 m。不排水抗剪强度的均值和标准差分别为

μ（h）=μ+γhb+dμ

σ（h）=σ+dexp（σ）

{（μ+σ）[exp（σ）-1]+σ}（8）

2.3 水泥土堤坝边坡可靠度计算分析流程

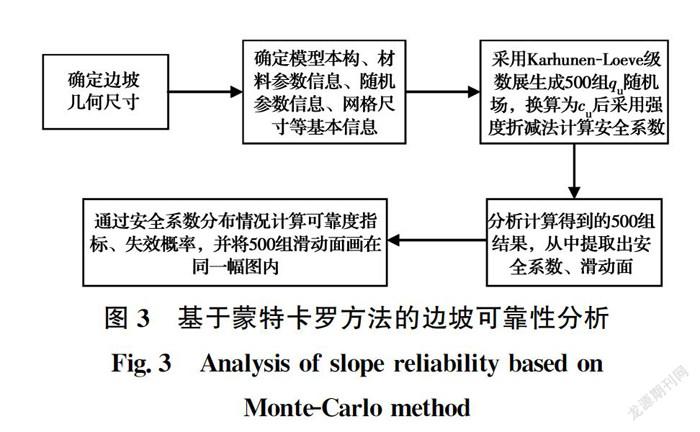
采用Karhunen-Loeve级数展开法离散随机场，每一工况生成500次随机场，结合蒙特卡洛模拟和强度折减法分析堤坝边坡失效概率，主要分析计算流程如图3所示，其中，强度折减法将边坡安全系数定义为使边坡刚好达到临界破坏状态时对其强度的折减程度。采用Mohr-Coulomb破坏准则时，其折减的强度参数是黏聚力c和内摩擦角φ（对于本例的不排水条件，仅折减黏聚力c），一般通过二分法迭代计算，通过不断扩大（或缩小）折减值，直至折减系数的上下限满足精度要求，将安全系数F定义为初始黏聚力c和破坏时的黏聚力c之比，即F=c/c。

随后统计一个工况内500组随机场模型计算结果，可得到安全系数的分布，并借此计算可靠指标、失效概率。

若安全系数的分布呈正态分布，则可靠指标

β=μ-1σ（9）

当安全系数呈对数正态分布时

β=lnμ1+Vln（1+V）（10）

式中：β为可靠指标;μ为500组安全系数均值;σ为500组安全系数标准差，V=σ /μ。利用可靠指标β与失效概率P之间的数学关系，可以用式（11）计算出可靠指标。

P=1-Φ（β）（11）

3 3种随机场模型对比

3.1 3种随机场模型实现情况对比

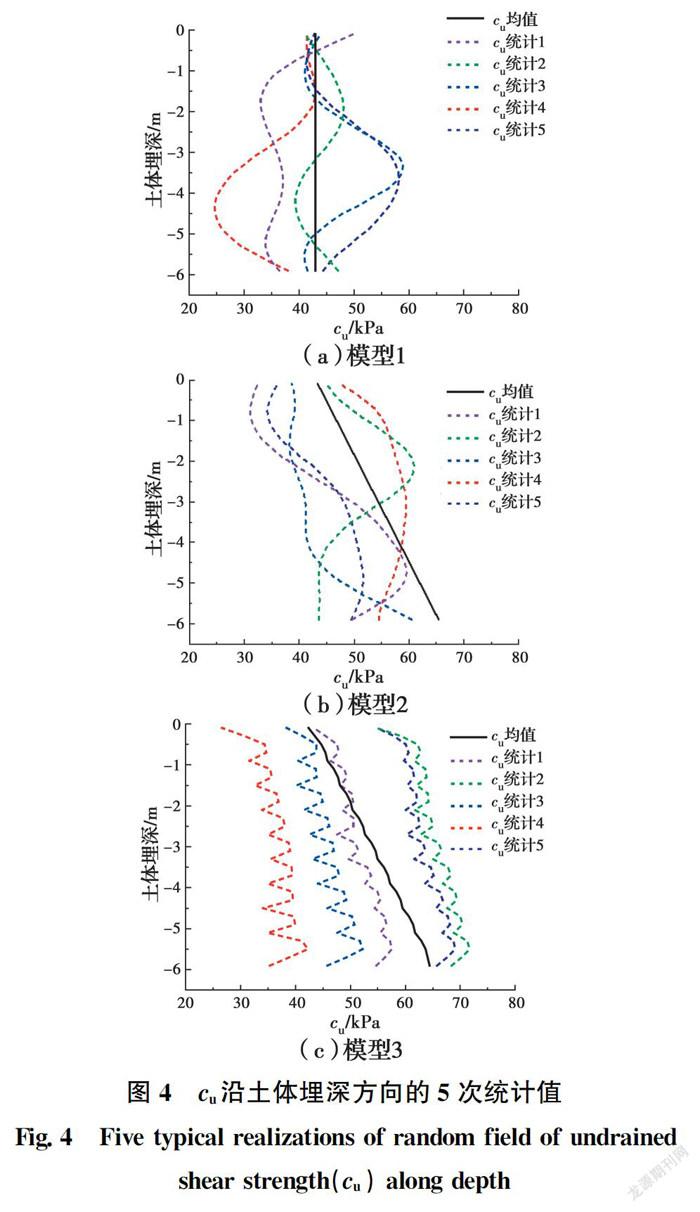
图4为3个模型堤坝土部分同一竖线上（参考图5（a）、（b），y=0平面上、x=3.6 m这条线）不同c的统计值（c=q/2）。可以看出，对于模型1，c大小随深度并无明显增加趋势，但沿深度呈现出随机波动趋势，且波动幅度较大。模型2呈现出c均值随深度增加的趋势，能够在一定程度上表征土体的非平稳特征。

模型3则表现出了沿深度增加和周期性波动的趋势，波动幅度明显小于模型1和模型2。这种周期性波动的原因是：土体不排水抗剪强度c沿深度方向有增加的趋势，但由于排水板加速局部的排水固结，使得局部强度最高，局部强度最大值即为排水板铺设位置，远离排水板则强度减小。这一效果与前述试验规律基本一致，且随着深度的增加，波动幅度增大，说明模型3的c均值沿深度方向增加。

图5为模型3三维网格不排水抗剪强度c分布结果，采用局部平均方法得到，图5（b）、（c）分别为三维模型的两方向上的断面，排水板铺设方向平行于边坡横截面，其横截面分布在三维边坡内的铺设点为图5（b）中的白点，可以看出，排水板四周土体的强度最高，随着离排水板距离的增加，土体强度逐渐降低，也基本符合前文所述研究规律。在平行于排水板方向，边坡横截面上，不排水抗剪强度c分布则近似于深度趋势随机场，在深度方向上呈增大的趋势，波动性亦很强。

3.2 3种随机场模型计算结果对比

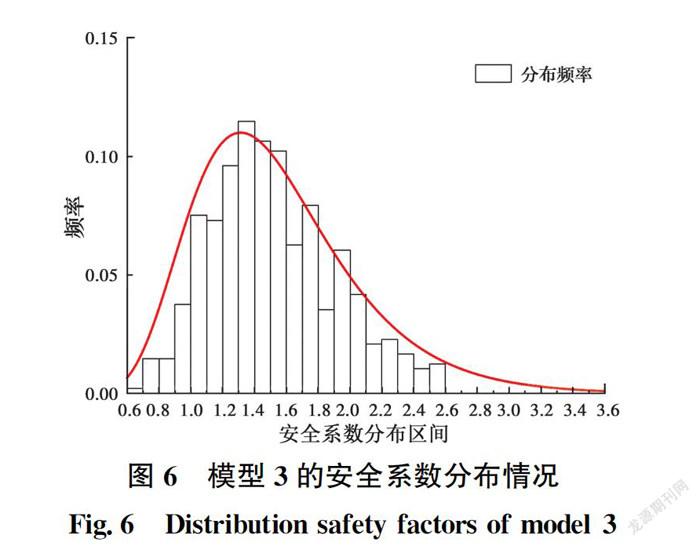
对上述3种典型工况分别进行500组蒙特卡洛模拟，利用强度折减法得出500组安全系数，模型3的安全系数分布情况如图6所示，对分布情况进行K-S检验发现，采用对数正态分布拟合时，其p=1，说明对数正态分布符合较好。经检验，其他工況安全系数分布同样符合对数正态分布。

模型1、模型2、模型3分别对应的可靠指标为1.34、2.79、1.30。从式（5）可见，模型2深度趋势模型的各项均为正，强度不存在衰减，理论上是“最安全”的工况，结果也验证了这一点。

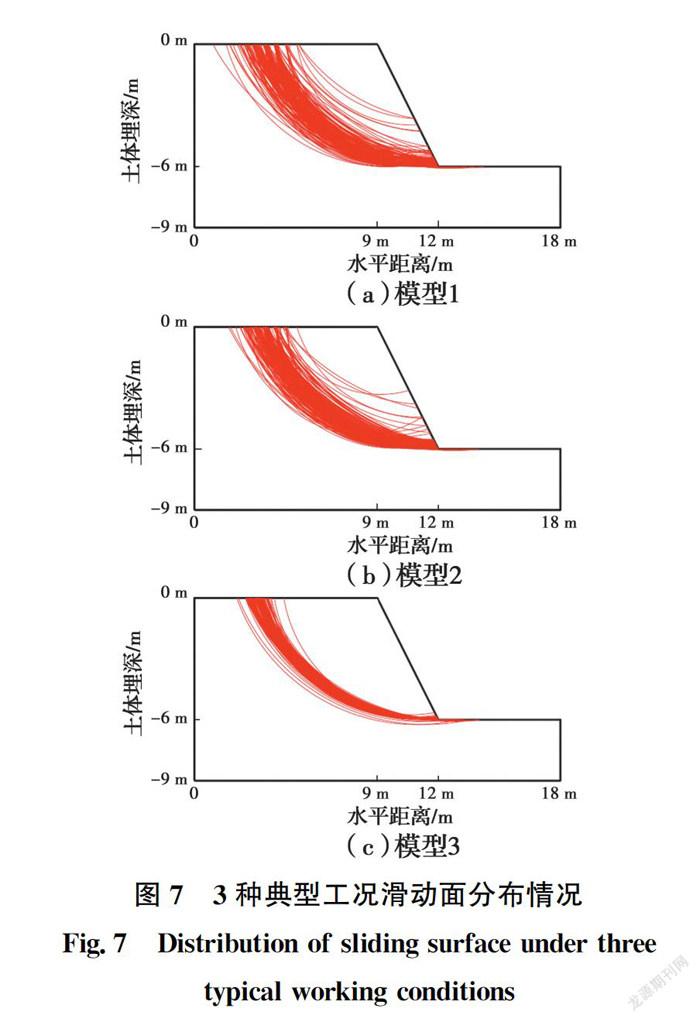
参考李剑等的做法，选取边坡达到极限状态时所有垂线上最大剪应变增量的位置，通过最小二乘法拟合圆弧滑动面，3种典型工况的滑动面分布结果如图7所示。3种典型工况的边坡滑动面都主要发生在水泥土堤坝土体内，但模型1、模型2的离散性更强，滑动面顶端与坡顶距离不一，滑动体体积也差距较大，模型3的滑动面则主要为从坡底贯穿坡顶的滑动面，分布集中。

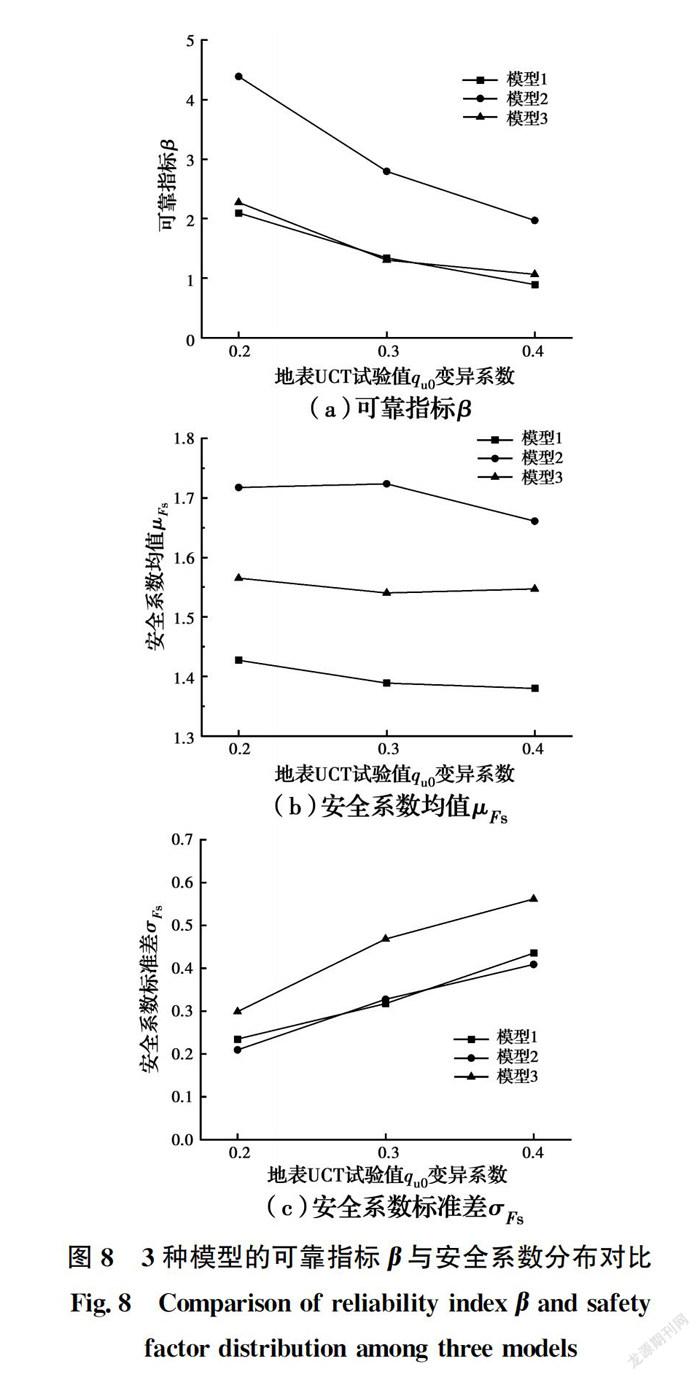
为了探究地表UCT实验值q的变异系数对模型结果的影响，分别对3种模型加算COV=0.2、0.4的工况，其最终结果如图8所示，随着变异系数的增加，3种模型计算得到的安全系数标准差增大，而安全系数均值变化不明显，导致可靠指标均减小。3种工况的安全系数均值μ分别为1.39、1.70、1.55。若仅考虑安全系数均值μ，3种工况均能满足规范要求，但可靠度仅模型2（深度趋势）能满足，并且模型3的安全系数离散程度高，变异性强，采用确定性分析或者平稳随机场模型偏于危险，讨论模型3随机分布情况就显得更为重要。

3.3 趋势参数b对安全系数分布的影响

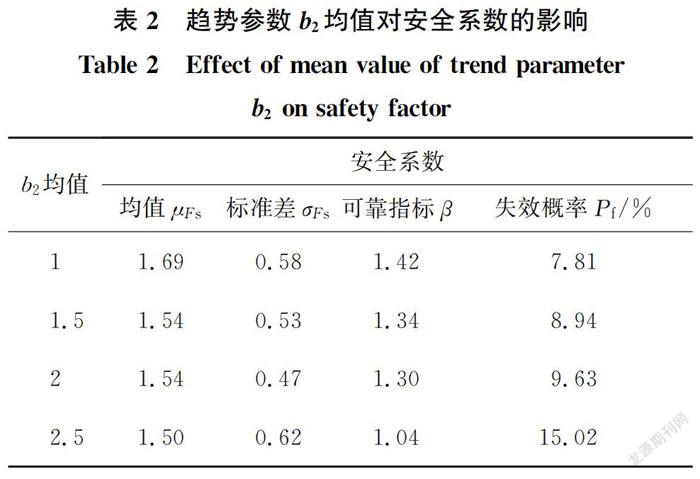
为了探究模型3中趋势参数b对安全系数分布的影响，分别单独取随机场离散公式（7）中b均值为1、1.5、2.5，b变异系数为0.1、0.2、0.4，其他参数保持不变，共6种工况，将其计算结果分别汇总于表2、表3，并与基础工况（b均值为2、变异系数为0.3）对比。从表中可以看出，无论是提高b的均值还是变异系数，最终都表现出可靠指标降低，失效概率增大的趋势。其中，b均值的增加带来式（7）中最终强度的减小，安全系数均值μ减小，标准差σ增大，变异性增强;b变异系数增大，安全系数均值μ基本未改变，但安全系数标准差σ增大，变异性增强。

4 结论

结合强度折减法、蒙特卡洛模拟方法，比较了3种随机场模型对水泥土堤坝边坡的失效风险和滑动面位置的影响，得到以下结论：

1）对于水泥土边坡的可靠度分析问题，采用平稳随机场或深度趋势随机场可能会高估边坡的可靠度，使计算结果偏于危险;即便是安全系数均值满足规范要求，但其标准差过大，最终的可靠指标并不能满足工程要求。

2）提出的不排水抗剪强度垂直排水板衰减非平稳模型既能考虑沿深度方向的趋势项，又能考虑垂直排水板方向的衰减趋势，综合表现为沿深度方向的近似周期性波动，与现有研究符合较好。在该模型中，趋势参数b对随机场模型的影响较大，当其值和标准差增加，最终都将降低计算模型的可靠指标，失效概率增大。

3）提出的不排水抗剪强度垂直排水板衰减非平稳模型的边坡破坏形式较为集中，大部分破坏面集中在堤坝土土体内，且多为从坡底贯穿坡顶的滑动面。

参考文献：

[1] GRIFFITHS D V， HUANG J S， FENTON G A. Influence of spatial variability on slope reliability using 2-D random fields [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2009， 135（10）： 1367-1378.

[2] PHOON K K， KULHAWY F H. Characterization of geotechnical variability [J]. Canadian Geotechnical Journal， 1999， 36（4）： 612-624.

[3] 张明， 赵有明. 基于随机场理论的吹填土土性参数空间变异性[J]. 中国港湾建设， 2012， 32（3）： 7-9， 21.

ZHANG M， ZHAO Y M. Spatial variability of property parameters of dredged fill based on random field theory [J]. China Harbour Engineering， 2012， 32（3）： 7-9， 21. （in Chinese）

[4] 周洋， 蒲诃夫， 李展毅， 等. 水平排水板-真空预压联合处理高含水率疏浚淤泥模型试验研究[J]. 岩石力学与工程学报， 2019， 38（Sup1）： 3246-3251.

ZHOU Y， PU H F， LI Z Y， et al. Experimental investigations on treatment of dredged slurry by vacuum-assisted prefabricated horizontal drains [J]. Chinese Journal of Rock Mechanics and Engineering， 2019， 38（Sup1）： 3246-3251. （in Chinese）

[5] 张文彬， 王贤奔， 谢锦波， 等. 水平排水板真空预压法处理吹填流泥试验研究[J]. 水运工程， 2016（7）： 122-127.

ZHANG W B， WANG X B， XIE J B， et al. Experimental study on dredger fill flow mud improved by vacuum preloading method employing horizontal drains [J]. Port & Waterway Engineering， 2016（7）： 122-127. （in Chinese）

[6] 高會强. 真空预压下塑料排水板有效影响范围的研究分析[D]. 广州： 华南理工大学， 2017.

GAO H Q. Study on the effective range of plastic vertical drain under vacuum preloading [D]. Guangzhou： South China University of Technology， 2017. （in Chinese）

[7] 曹宇春. 固结后软黏土不排水抗剪强度简化计算方法比较[J]. 土木工程学报， 2014， 47（10）： 107-116.

CAO Y C. A comparison of simplified calculation methods of undrained shear strength of soft clays after consolidation [J]. China Civil Engineering Journal， 2014， 47（10）： 107-116. （in Chinese）

[8] 蒋水华， 李典庆， 周创兵， 等. 考虑参数空间变异性的非饱和土坡可靠度分析[J]. 岩土力学， 2014， 35（9）： 2569-2578.

JIANG S H， LI D Q， ZHOU C B，et al. Reliability analysis of unsaturated slope considering spatial variability [J]. Rock and Soil Mechanics， 2014， 35（9）： 2569-2578. （in Chinese）

[9] 郑俊杰， 乔雅晴， 章荣军. 被动加固区参數变异性对软土深基坑变形行为的影响[J]. 土木与环境工程学报（中英文）， 2019， 41（6）： 1-8.

ZHENG J J， QIAO Y Q， ZHANG R J. Effect of spatial variability of engineering properties on holistic performance of passive zone improvement for deep excavation in soft soil [J]. Journal of Civil and Environmental Engineering， 2019， 41（6）： 1-8. （in Chinese）

[10] 蒋水华， 曾绍慧， 杨建华， 等. 不排水抗剪强度非平稳随机场模拟及边坡可靠度分析[J]. 岩土力学， 2018， 39（3）： 1071-1081.

JIANG S H， ZENG S H， YANG J H， et al. Slope reliability analysis by simulation of non-stationary random field of undrained shear strength [J]. Rock and Soil Mechanics， 2018， 39（3）： 1071-1081. （in Chinese）

[11] GRIFFITHS D V， HUANG J， FENTON G A. Probabilistic slope stability analysis using RFEM with non-stationary random fields [C]//Geotechnical Safety and Risk V， 2015： 704-709.

[12] 祁小辉， 李典庆， 周创兵， 等. 考虑不排水抗剪强度空间变异性的条形基础极限承载力随机分析[J]. 岩土工程学报， 2014， 36（6）： 1095-1105.

QI X H， LI D Q， ZHOU C B， et al. Stochastic analysis of ultimate bearing capacity of strip footing considering spatial variability of undrained shear strength [J]. Chinese Journal of Geotechnical Engineering， 2014， 36（6）： 1095-1105. （in Chinese）

[13] LI D Q， QI X H， PHOON K K， et al. Effect of spatially variable shear strength parameters with linearly increasing mean trend on reliability of infinite slopes [J]. Structural Safety， 2014， 49： 45-55.

[14] 豆红强， 王浩. 非平稳随机场下饱和渗透系数空间变异性的无限长边坡稳定概率分析[J]. 土木工程学报， 2017， 50（8）： 105-113， 128.

DOU H Q， WANG H. Probabilistic analysis of spatial variability of saturated hydraulic conductivity on infinite slope based on the non-stationary random field [J]. China Civil Engineering Journal， 2017， 50（8）： 105-113， 128. （in Chinese）

[15] LI D Q， QI X H， CAO Z J， et al. Reliability analysis of strip footing considering spatially variable undrained shear strength that linearly increases with depth [J]. Soils and Foundations， 2015， 55（4）： 866-880.

[16] SHU S， GAO Y F， WU Y X， et al. Bearing capacity and reliability analysis of spudcan foundations embedded at various depths based on the non-stationary random finite element method [J]. Applied Ocean Research， 2020， 100： 102182.

[17] WU Y X， ZHOU X H， GAO Y F， et al. Effect of soil variability on bearing capacity accounting for non-stationary characteristics of undrained shear strength [J]. Computers and Geotechnics， 2019， 110： 199-210.

[18] ZHANG R J， HASAN M S M S， ZHENG J J， et al. Effect of spatial variability of engineering properties on stability of a CSMC embankment [J]. Marine Georesources & Geotechnology， 2018， 36（1）： 91-99.

[19] LEE F H， LEE Y， CHEW S H， et al. Strength and modulus of marine clay-cement mixes [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2005， 131（2）： 178-186.

[20] LIU Y， CHEN E J， QUEK S T， et al. Effect of spatial variation of strength and modulus on the lateral compression response of cement-admixed clay slab [J]. Géotechnique， 2015， 65（10）： 851-865.

[21] 瞿秀祥， 林杭， 王敏， 等. FLAC V边坡稳定剪切强度折减法的多线程并行算法[J]. 铁道科学与工程学报， 2018， 15（7）： 1693-1699.

QU X X， LIN H， WANG M， et al. Study on the slope stability shear strength reduction method based on the multi-thread parallel computing technology in the FLAC V software [J]. Journal of Railway Science and Engineering， 2018， 15（7）： 1693-1699. （in Chinese）

[22] 李劍， 陈善雄， 余飞. 基于最大剪应变增量的边坡潜在滑动面搜索[J]. 岩土力学， 2013， 34（Sup1）： 371-378.

LI J， CHEN S X， YU F. A method for searching potential failure surface of slope based on maximum shear strain increment [J]. Rock and Soil Mechanics， 2013， 34（Sup1）： 371-378. （in Chinese）

[23] 水利水电工程边坡设计规范： SL 386—2007 [S]. 北京： 中国水利水电出版社， 2007.

Design code for engineered slopes in water resources and hydropower projects： SL 386-2007 [S]. Beijing： China Water & Power Press， 2007. （in Chinese）

[24] 公路工程结构可靠度设计统一标准： JTG 2120—2020 [S].北京： 人民交通出版社， 2020.

Unified standard for reliability design of highway engineering structures： JTG 2120-2020 [S]. Beijing： China Communications Press， 2020. （in Chinese）

[25] 公路路基设计规范： JTG D30—2015 [S]. 北京： 人民交通出版社， 2015.

Specifications for design of highway subgrades： JTG D30-2015 [S]. Beijing： China Communications Press， 2015. （in Chinese）

（编辑 胡玲）