一类笛卡儿积图中可去边的研究

马云凤

（闽南师范大学数学与统计学院,福建 漳州 363000）

记图G的顶点集和边集分别为V(G)和E(G).设M是E(G)的一个子集，若该边子集中的任意两条边在图G中均不相邻，则称M为图G的匹配.若匹配M的某条边与顶点v关联，则称顶点v是M饱和的.若图G的每个顶点均为M饱和的，则称M为图G的完美匹配.引入匹配覆盖图的定义：若图G为有两个以上顶点的连通图，并且其任意一条边都属于某个完美匹配，则称图G为匹配覆盖图.图G为匹配覆盖图，e为G中一条边，若G-e仍为匹配覆盖图，则e为图G的可去边.

假设k是一个满足的整数，图G是一个有完美匹配的连通图，若图G中任意包含k条边的匹配都属于一个完美匹配，则称图G是k-可扩图.匹配覆盖图显然就是1-可扩图.容易看出对于2-可扩图，所有的边都是可去边.1992年，Györi 等[1]证明了若G1是一个k-可扩图,G2是一个l-可扩图，则它们的笛卡儿乘积图G1×G2是(k+l+1)-可扩图，其中；若G1是一个k-可扩图，G2是一个连通图，则它们的笛卡儿乘积图G1×G2是(k+1)-可扩图，其中1≤k≤一个顶点数至少为2m+2n+2 的有完美匹配的连通图被称为E(m,n)的，如果对于任意两个无公共边的匹配M和N，存在完美匹配F满足M⊆F且N∩F=∅，其中|M|=m，|N|=n.注意到图G是m-可扩的当且仅当它是E(m,0)的.2017年Aldred 等[2]证明了若m≥0 且G是E(m,1)的，则G×P2是E(m+1,0)和E(m,2)的.2-可扩的二部图，称为brace；三连通双临界图，称为brick，其中，双临界图是指去掉任意两个顶点后存在完美匹配的图.1983年Lovász[3]证明了每个brick（除K4和Cˉ6)都有一条可去边.1999年Lucchesi 等[4]证明了每个brick（除K4和Cˉ6）至少有Δ-2 条可去边，其中Δ是图的最大度.2015年，Carvalho等[5]证明了在顶点数至少为六的brace中，每一条边都为可去边.

设图G的顶点集V(G)={v1,v2,…,vn}，G1,G2,…,Gl是l个与G同构的图，其顶点集分别为{v11,v21,…,vn1},{v12,v22,…,vn2},…,{v1l,v2l,…,vnl}，图H=G×Pl是将G1,G2,…,Gl用边v1iv1,i+1,v2iv2,i+1,…,vnivn,i+1,i=1,…,l-1连接得到.记[l]=1,…,l-1.若图G为有完美匹配的图，取其一个完美匹配，记为M，M在图Gi中的限制，记为Mi（即M与Gi的交为Mi），i∈[l].对于任一有完美匹配的连通图G（δ(G)≥2）和包含l个顶点的路Pl（l≥4），证明了它们的笛卡儿乘积图G×Pl为匹配覆盖图，且每条边都是可去边，其中δ(G)是图G的最小度.

1 主要结论与证明

定理1设图G为有完美匹配的连通图，且δ(G)≥2，Pl为包含l个顶点的路（l≥4），则图G×Pl为匹配覆盖图.

证明下面将根据l的奇偶性进行分类讨论.

情况1l为偶数，设l=2m.

设E其结构如图1所示.

图1 Ea和Eb的结构Fig.1 The structure of Ea and Eb

情况1.1e∈Ea，容易验证Ea是图G×P2m的完美匹配，并且e∈Ea.

情况1.2e∈Eb，不妨设e=vs,2ivs,2i+1,容易验证Mb=(Ea-E[G2i-1,G2i]-E[G2i+1,G2i+2]) ∪M2i-1∪E[G2i,G2i+1]∪M2i+2是图G×P2m的完美匹配，并且e∈Mb.

情况1.3e∈不妨设e=vs,2ivt,2i，容易验证是图G×P2m的完美匹配，并且e∈Mc.

所以，G×P2m中任意一条边都属于某个完美匹配.

情况2l为奇数，设l=2m+1.

Ea和Eb的定义同上.记Eb*=Eb∪E[G2m,G2m+1]，则根据G×P2m+1的对称性可知，Ea和Eb*这两类边有类似的结构，E(G2m+1)和这两类边有类似的结构，因此，根据e在G×P2m+1的位置，可以只考虑以下3种情况.

情况2.1e∈Ea，容易验证Ea∪M2m+1是图G×P2m+1的完美匹配，并且e∈Ea∪M2m+1.

情况2.2e∈不妨设e=vs,2ivt,2i，容易验证Mc∪M2m+1是图G×P2m+1的完美匹配，并且e∈Mc∪M2m+1.

情况2.3e∈不妨设e=vs,2i-1vt,2i-1，同理，容易验证Mc∪M2m+1是图G×P2m+1的完美匹配，并且e∈Mc∪M2m+1.

所以，G×P2m+1中任意一条边都属于某个完美匹配.

综上所述，G×Pl中任意一条边都属于某个完美匹配,即G×Pl为匹配覆盖图.

定理2设图G为有完美匹配的连通图，且δ(G)≥2，Pl为包含l个顶点的路（l≥4），则图G×Pl的每条边都是可去边.

证明只需证明对∀e′∈E(G×Pl)，G×Pl-e′中任意一条边都属于某个完美匹配.下面将根据l的奇偶性进行分类讨论.本定理的证明中出现的Ea、Eb、Eb*、Mb、Mc皆如定理一中证明所定义.

情况1l为偶数，设l=2m.

当l为偶数，根据e在G×P2m-e′的位置，可以只考虑以下3种情况.

情况1.1e∈Ea，若e′∉Ea，容易验证Ea是图G×P2m-e′的完美匹配，并且e∈Ea.否则，e′∈Ea，不妨设e′=vj,2i-1vj,2i且vk∈NG(vj)，则C1=vj,2i-1vj,2ivk,2ivk,2i-1vj,2i-1是一个Ea交错圈，容易验证E(C1)ΔEa是图G×P2me′的完美匹配，并且e∈E(C1)ΔEa.

情况1.2e∈Eb，不妨设e=vs,2ivs,2i+1，若e′∉Mb，容易验证Mb是G×P2m-e′的完美匹配，且e∈Mb；否则，e′∈Mb=(Ea-E[G2i-1,G2i]-E[G2i+1,G2i+2]) ∪M2i-1∪E[G2i,G2i+1]∪M2i+2，即e′∈(Ea-E[ ]

G2i-1,G2i-E[G2i+1,G2i+2])∪E[G2i,G2i+1]或e′∈M2i-1∪M2i+2.

情况ae′∈(Ea-E[G2i-1,G2i]-E[G2i+1,G2i+2]) ∪E[G2i,G2i+1]，则根据本定理情况1.1 的方法，G×P2me′存在完美匹配包含e.

情况be′∈M2i-1∪M2i+2，不妨设e′∈M2i+2且e′=vj,2i+2vk,2i+2，则C2=vj,2ivj,2i+1vj,2i+2vk,2i+2vk,2i+1vk,2ivj,2i是一个Mb交错圈.若e∉C2，容易验证E(C2)ΔMb是图G×P2m-e′的完美匹配，并且e∈E(C2)ΔMb（局部结构如图2所示）.否则，e∈C2，不妨设e=vk,2ivk,2i+1（即s=k），由于δ(G)≥2，所以存 在 顶点vl∈NG(vk).令C3=vk,2i-1vk,2ivk,2i+1vk,2i+2vl,2i+2vl,2i+1vl,2ivl,2i-1vk,2i-1，显然C3是一个Ea交错圈，容易验证E(C3)ΔEa是图G×P2me′的完美匹配，并且e∈E(C3)ΔEa（局部结构如图3所示）.

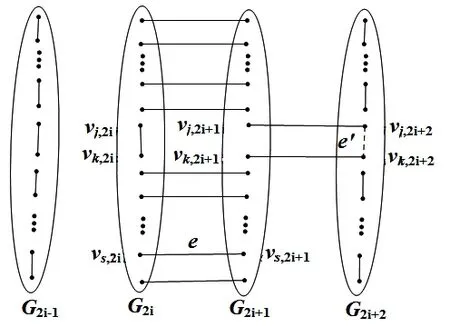
图2 E(C2)ΔMb的局部结构Fig.2 Part of E(C2)ΔMb

图3 E(C3)ΔEa的局部结构Fig.3 Part of E(C3)ΔEa

情况1.3e∈不妨设e=vs,2ivt,2i.若e′∉Mc，容易验证Mc是G×P2m-e′的完美匹配，并且e∈Mc.否则，e′∈Mc=(Ea-{vs,2i-1vs,2i,vt,2i-1vt,2i}) ∪{vs,2i-1vt,2i-1,vs,2ivt,2i}，即e′∈Ea-{vs,2i-1vs,2i,vt,2i-1vt,2i}或e′∈{vs,2i-1vt,2i-1,vs,2ivt,2i}.

情况ce′∈Ea-{vs,2i-1vs,2i,vt,2i-1vt,2i}，则根据本定理情况1.1的方法，G×P2m-e′存在完美匹配包含e.

情况de′∈{vs,2i-1vt,2i-1,vs,2ivt,2i}，又因为e′≠e，所以e′=vs,2i-1vt,2i-1,i∈[m].当i∈[m-1]时，由于δ(G)≥2，l≥4，所以存在顶点vj∈NG(vs),vk∈NG(vt).令C4=vj,2i-1vj,2ivj,2i+1vj,2i+2vs,2i+2vs,2i+1vt,2i+1vt,2i+2vk,2i+2vk,2i+1vk,2i vk,2i-1vt,2i-1vt,2ivs,2ivs,2i-1vj,2i-1，显然C4是一个Ea交错圈，容易验证E(C4)ΔEa是图G×P2m-e′的完美匹配，并且e∈E(C4)ΔEa（局部结构如图4所示）.当i=m时，有e′=vs,2m-1vt,2m-1，e=vs,2mvt,2m，同 时，C5=vs,2m-3vs,2m-2vs,2im-1vs,2mvt,2mvt,2m-1vt,2m-2vt,2m-3vs,2m-3是一个Ea交错圈，容易验证E(C5)ΔEa是图G×P2m-e′的完美匹配，并且e∈E(C5)ΔEa（局部结构如图5所示）.

图4 E(C4)ΔEa的局部结构Fig.4 Part of E(C4)ΔEa

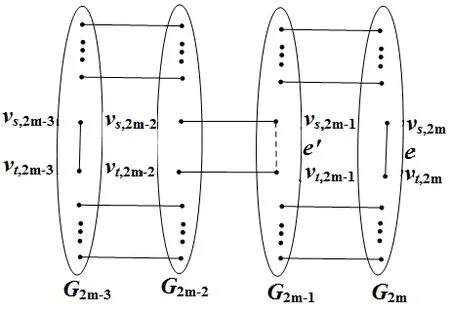
图5 E(C5)ΔEa的局部结构Fig.5 Part of E(C5)ΔEa

所以，对∀e′∈E(G×P2m)，G×P2m-e′中任意一条边都属于某个完美匹配.

情况2m为奇数，设l=2m+1.

首先考虑l≥7 的情况.在定理1 的证明过程中，当l为奇数时，根据e在G×P2m+1的位置，只考虑了和这三种情况.根据G×P2m+1的对称性可知，E(G2m) 和这两类边有类似的结构，E(G2m-1)和这两类边有类似的结构.因此，可以只考虑和这三种情况.在以上任一种情况中，若e′∈E(G2m+1)，根据本定理情况1.2 中情况b 的方法（局部结构类似于图2所示），G×P2m+1-e′存在完美匹配包含e.否则e′∉E(G2m+1)，即e′∈E[G2m,G2m+1]或e′∈E(G×P2m).当e′∈E[G2m,G2m+1]时，显然G×P2m+1-e′存在完美匹配包含e.当e′∈E(G×P2m)时，根据l为偶数时的结论，G×P2m-e′存在完美匹配包含e，则G×P2m+1-e′存在完美匹配包含e.

其次考虑l=5 的情况.此时E(G2m-1)=E(G3)，结合l≥7 的证明可知，需要考虑e∈Ea和e∈E(G1)∪E(G2)∪E(G3)的情况.e∈Ea和e∈E(G1)∪E(G2)的情况同l≥7，只需考虑e∈E(G3).设e=vs,3vt,3，根据定理一情况2.3，容易验证是G×P5的完美匹配，并且e∈Mc∪M5.若e′∉Mc∪M5，显然G×P5-e′存在完美匹配包含e.否则，e′∈Mc∪M5，即e′∈Mc或e′∈M5.

情况2.1e′∈Mc，根据l为偶数时的结论，G×P4-e′存在完美匹配包含e，则G×P5-e′存在完美匹配包含e.

情况2.2e′∈M5，若e′=vk,5vs,5（或e′=vj,5vt,5），其中vk,5是vs,5的异于vt,5的邻点（或vj,5是vt,5的异于vs,5的邻点），容易验证是G×P2m+1-e′的完美匹配，并且e∈M′（如图6所示）.否则，e′∈M5-vk,5vs,5-vj,5vt,5，根据本定理情况1.2中情况b的方法（局部结构类似于图2所示），G×P2m+1-e′存在完美匹配包含e.

图6 M′的结构Fig.6 The structure of M′

所以，对∀e′∈E(G×P2m+1)，G×P2m+1-e′中任意一条边都属于某个完美匹配.

综上所述，对∀e′∈E(G×Pl)，G×Pl-e′中任意一条边都属于某个完美匹配，即该图的每一条边都是可去边.

注根据E(1,1)的定义，定理2 可以叙述为：对于任一有完美匹配的连通图G（δ(G)≥2）和包含l个顶点的路Pl（l≥4），它们的笛卡儿乘积图G×Pl是E(1,1)的.