燃料组件简化梁模型剪切系数初步研究

沈平川， 黄旋， 刘建， 张珂， 皇甫聿昭

（中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都 610041）

0 引言

燃料组件结构复杂，非线性因素多，因此一般使用简化梁模型进行反应堆、燃料组件地震和LOCA时程动力分析，以确保事故工况下的燃料组件结构安全。

燃料组件简化梁模型通常使用试验测试的方式获取梁截面参数，其中测试得到的剪切系数一般高达几百，这与燃料组件主要结构形式——薄壁管的剪切系数为2相比，差异较大。

Timoshenko[1]的梁理论中首次考虑了梁的剪切变形。对于单根梁结构的剪切系数计算方法文献较多，如Cowper[2]和王乐等[3]。但是对于燃料组件这样的结构形式，简化梁模型出现的异常剪切系数的情况，目前尚无相关研究。因此弄清该异常剪切系数的物理本质，给出计算方法，具有学术和工程价值。

1 初步研究线性结构模型

国内核电站常用燃料组件结构如图1所示。两端为上下管座用于燃料组件的安装定位。管座之间由若干平行的导向管和仪表管连接，管束跨中间焊接布置若干格架，把管束分为若干节段，构成燃料组件的骨架。燃料棒由格架的刚凸和弹簧片夹持，具有滑移摩擦和预紧接触等非线性因素。

图1 燃料组件结构和简化梁模型

由于燃料组件的复杂性，本文着力于开展燃料组件简化梁模型剪切系数的初步研究，重点在于厘清其产生的主要物理本质。因此根据燃料组件结构特点，忽略其结构复杂性和非线性因素，建立初步理论研究用的简单线性分析模型。

初步研究线性结构模型包含3根相同的管，形成管束，在平面内均匀间距平行布置，格架采用刚性面假设，把管束均分为3个节段。在外部边界条件方面，使用最简单的悬臂梁模式，便于简化计算过程，如图2所示。

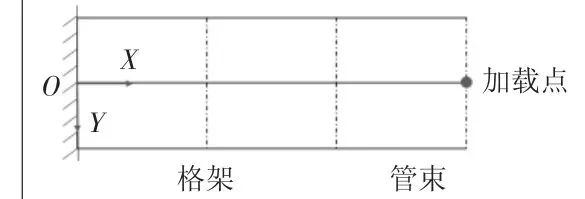
图2 初步研究线性结构模型

2 有限元计算剪切系数方法

对于初步理论分析模型，使用有限元方法建立计算模型，在自由端施加载荷，计算加载点的位移响应，进而计算简化梁模型的截面参数。

在自由端沿轴线X方向施加力Fx进行拉伸，得到加载点的轴向位移为

下面进行案例计算，假设初步理论分析模型的总长度Lall为0.6 m，管之间横向间隔距离Dist为0.1 m，管外径D为12 mm，壁厚t为5 mm，弹性模量E为200 GPa，泊松比ν为0.3。自由端的加载力为1000 N，力矩为1000 N·m。

使用本节计算方法可以得到简化梁的截面参数如表1所示。

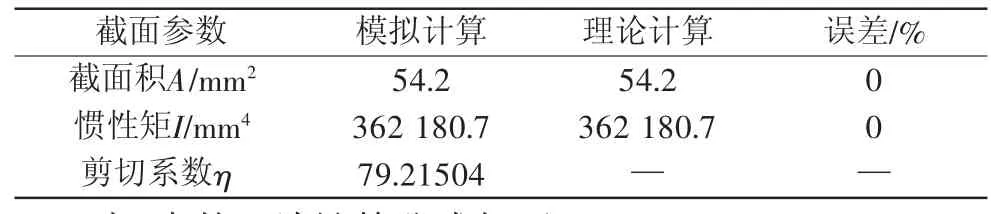
表1 简化梁截面参数计算结果

表1中的理论计算公式如下：

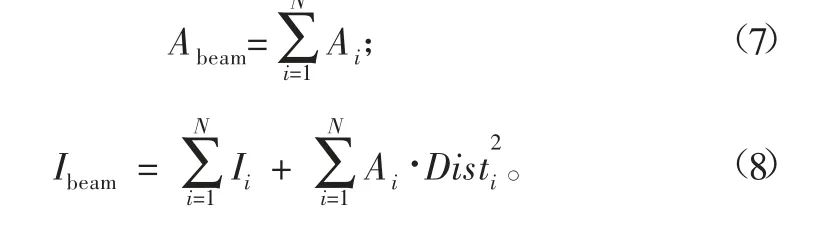
式中：Ai、Ii和Disti分别为管束中第i根管的截面积、惯性矩和到中性面的距离；N为管束中管数量。

根据表1中截面参数，建立单根简化梁模型进行检验。采取悬臂梁形式，在自由端施加同样3种载荷，得到加载点的位移响应结果对比，如表2所示。

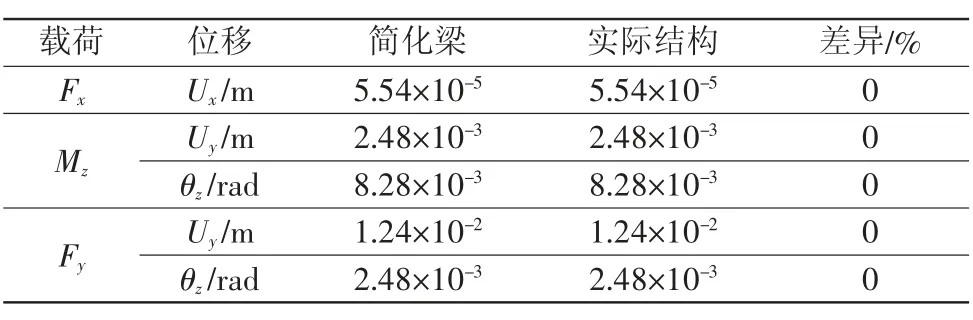
表2 位移结果验证

由表2可以看出，单根简化梁模型和实际结构对于自由端的外部载荷，其端部位移响应结果相同。验证了本节简化梁截面参数的计算方法，可以处理悬臂梁+端部集中加载这样的结构形式下的等效问题。

从表1可看出，对于燃料组件式的分节管束结构，在假设每个格架为刚性面的情况下，简化梁的截面积和惯性矩与传统理论公式计算结果相同，但是剪切系数数值较大，与薄壁管剪切系数数值2之间的差异较大。下节将针对该问题，开展剪切系数的物理意义和理论计算方法研究。

3 弯矩分解法计算剪切系数研究

对于梁结构，可以把梁按长度分为若干节段，对于每一节段分别计算在节段端部载荷作用下的内部相对变形，最后将每一节段的内部相对变形串联组合起来，得到梁结构的整体变形，即整体变形是所有部分变形的组合，如图3所示。

图3 梁整体和节段内部相对变形

每一节段内部相对变形的计算，可以采用一端固支、一端自由的悬臂结构，在自由端施加交界节点受到的下一节段传递来的载荷，得到节段内每一点对于固支端节点的相对位移。

选取梁结构随意一个节段，假设自由端受到的载荷为侧向集中力Fj和弯矩Mj，如图4所示。

图4 节段加载示意图

则该节段任意位置的弯矩Mz（x）为：

在自由端（x=L）节点相对于固定端节点的弯曲变形转角和侧向位移：

由自由端节点的相对转角Uy′（L）可以看出，转角仅受到平均弯矩的作用，除此外的其他部分弯矩，不会造成自由端节点的转动，仅造成其侧向平动（侧向滑移）。

因此，为了适应燃料组件式的分节管束结构特点，对梁上的弯矩采用了新的分解方式，分解为纯弯曲 型 弯 矩M1（x）和侧向滑移型弯矩M2（x）两部分（如图5）：

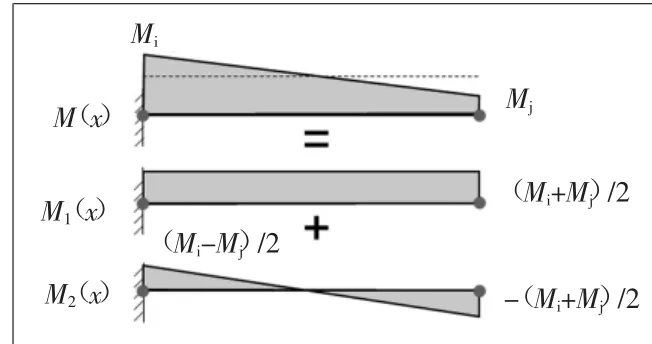
图5 弯矩分解示意图

M1（x）弯矩为定值，等于分段两端节点处弯矩的平均值，在其作用下节段梁发生纯弯曲变形。

在M2（x）弯矩作用下，该节段任意位置相对于固定端节点的弯曲变形转角和侧向位移分别为：

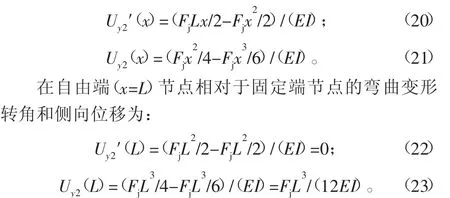
可以看出，在M2（x）弯矩作用下，节段梁的自由端节点相对于固定端节点的弯曲变形转角为零，仅发生侧向位移。节段梁的整体表现为两端发生侧向滑移，故命名为侧向滑移型弯矩。

由上节可知，简化梁的截面惯性矩为纯弯曲对应的惯性矩Ibeam，数值较大。因此M2（x）弯矩作用下的简化梁弯曲变形小于实际结构弯曲变形，差值如下：

对于上节中有限元计算范例，使用本节公式进行简化梁剪切系数计算，结果对比如表3所示。

由表3对比可知，按式（27）计算的简化梁剪切系数与有限元计算结果完全一致，验证了分节管束结构简化梁剪切系数的物理意义和计算公式的正确性。

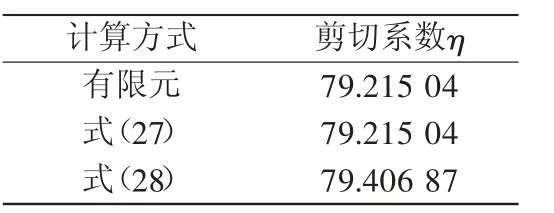
表3 范例剪切系数计算结果

4 结论

对于燃料组件式的分节管束结构，简化梁模型存在剪切系数较大的问题。对该剪切系数的物理实质和计算方法开展初步研究。忽略燃料组件结构复杂性和非线性，建立初步研究线性结构模型。

通过弯矩分解的方法，把梁弯矩分解为纯弯曲型和侧向滑移型两部分。侧向滑移型弯矩仅造成侧向滑移变形，在分节管束结构中不产生额外的轴向力，因此对应的惯性矩中无轴向力偏离中性轴的偏置项，大大小于纯弯曲对应的惯性矩。简化梁的截面参数为较大的纯弯曲惯性矩，侧向滑移型弯矩作用下的简化梁弯曲变形小于实际结构，只能加大简化梁剪切系数来增大剪切变形以弥补弯曲变形差值。

最后根据简化梁剪切系数的物理实质，给出由结构参数计算简化梁剪切系数的方法，与有限元计算结果一致，验证了该方法的正确性。