基于几何均值的三维网格滤波方法

许晨炀，彭武杰，刘帆，2，毛志红

（1.五邑大学 智能制造学部，广东 江门 529000；2.广东奥普特科技股份有限公司，广东 东莞 523846）

1 简介

1.1 研究背景

随着科技的不断发展，数字扫描仪的使用越来越普遍，人们通过数字扫描仪来获取三维物体表面的数据也越来越容易，根据获取数据样本密度的不同，表面数据一般主要分为点云和网格数据，点云数据有着高的采样密度，接近于原始模型，其缺点在于拓扑关系的不明确以及庞大的待处理点数据；相反，网格数据有着明确拓扑关系以及稀疏的点数据。尽管其低密度的采样可能存在不能完整地描述模型的缺点，但这些缺点可以通过后期交互式3D模型重建及处理技术进行弥补。然而，无论是点云数据还是网格数据，在获取3D数据时，不可避免地会出现噪声，噪声的出现会严重影响模型的正确表示以及后续的重建过程，因此降噪就成为数字几何处理的关键步骤。

如前所述，网格数据作为一种基本的数据对象，其明确的拓扑关系降低了三维重建的数据结构的复杂度，有关网格数据三维重建中的降噪方法，前人已经做出了许多的研究工作。就目前所做的文献调研情况，针对网格数据中不同降噪方法的理论基础，大致可以分为3类。

第一类是基于微分几何的方法，这类方法不同于统计学方法，往往有着较高的复杂度。比如Zhao Huanxi[1]的高斯曲率流方法，通过计算点的高斯曲率值并设置判别条件来对不同区域进行降噪和特征保持，这种方法在一些具有尖锐特征的模型上有着比较好的处理效果，但算法所涉及的法向量的重定向以及高斯曲率的计算会使得算法的处理效率降低；微分几何的方法也应用于法向量的降噪和模型重构[2]，这类方法的主要特点就是使用曲面的微分方程作为理论基础进行曲面拟合和相关法向量的计算。

第二类是基于图像信号处理中的滤波，这类算法理论丰富且利于推广和延伸，是三维重建中相当重要的一部分内容。比如Fleishman[3]的双边滤波算法，通过空间距离权值和角度权值来进行权值平均，算法的复杂度低，有着比较好的降噪和特征保持效果，尤其在具有尖锐模型特征上表现明显（如CAD模型）；Lee Kai-Wah[4]的法向量重定向的双边滤波，通过对法向量进行双边滤波来重定向点的法向量，最后通过所求得的法向量来设计迭代公式，以此反求要更新的顶点位置；毛志红[5]在双边滤波上做出了一些改进，提出了一种基于Susan邻域的双边滤波算法，算法基于一个定义的Susan邻域进行双边滤波，在降噪和特征保持上有比较良好的效果；Yoshizawa[6]的NL-means算法，通过定义相似权来进行降噪处理，算法效果良好，但是全局算法本身的计算量庞大，处理的时间也随之剧增；夏锋[7]提出了一种基于相似区域块的估计方法，通过计算曲率、形状指数和形状直径函数构建高阶张量矩阵进行相似度的甄别，以此寻找相似块，从而重建点的法向量，最后通过2-邻域的最小二乘拟合平面，以此更新顶点位置，但文中仅仅进行了法向量的重定向，更新的步长仅由点到最小二乘法平面的距离求得，导致该方法鲁棒性不高。从图像中拓展的Lp范数滤波应用于三角网格也是近几年研究的热点内容[8-9，11]，范数滤波是一种优化求解器，求解器的关键在于范数对象的构建。

第三类是以特征提取为核心的滤波算法，这类滤波方法的主体还是图像滤波算法的应用推广，为了让滤波器具有更高的鲁棒性，这类算法在网格模型特征提取上做出了相当多的工作，但也大量增加算法的时间开销。如Fan Hanqi[10]的基于子邻域一致性的特征保持网格滤波算法，算法以点法向量的关系进行点聚类，进而将得到类的边界标记为特征，最后进行双边滤波；Lu Xuanquan[11]的鲁棒性的特征保持网格降噪算法的一大重要内容就是对特征点的识别、连接及重建，最后通过更新顶点位置完成滤波。

1.2 主要贡献

虽然模型降噪的方法还有很多，比如曲面逼近、曲面拟合、基于深度学习的法向滤波等[12-16]，但是效果良好的算法往往复杂度过高，时间开销大；而较低复杂度的算法对特征保持的效果往往不理想。基于对图像处理中的几何均值滤波的研究，本文提出了一种新颖的基于几何均值滤波的简单高效网格滤波算法，以第二类图像信号处理中滤波方法为基础进行延伸，应用高斯核函数及同态滤波思想提升滤波器的鲁棒性，在有效保持特征的同时，高效地去除噪声。

2 相关工作

2.1 预备知识

图1 原始网格模型和含噪声模型

三维测量仪器在扫描的过程中由于外界的因素及扫描仪或相机本身的原因不可避免地会产生噪声，在本文实验中，算法利用网格平均边长L来产生加性的高斯噪声，根据可能产生的随机噪声大小程度，将噪声按Noise∈（0，1）中的值来分级，定义Noise=（0～0.2）L时为轻度噪声，Noise=（0.2～0.5）L时为 中 度 噪 声，Noise=（0.5 ～1.0）L为重度噪声。

三角网格模型可以用三元组来表示，M=（VM，KM，PM），VM是所有顶点的集合；KM代表拓扑关系，包含顶点索引值、连接边和三角面片信息；PM表示顶点的属性信息，比如点空间位置、点法向量等[5]。网格数据中比较重要且明确的就是易获取的邻域信息（如图2），在KM中点p的1-邻域可以表示为N（p，1），2-邻域可以表示为N（p，2），以此类推，p的n-邻域可以表示为N（p，n）。

图2 网格点N-邻域索引示意图

2.2 二维图像滤波方法

几何均值滤波是图像处理中一种常见的滤波方法，几何均值滤波器对一副图像的复原表达式由下式给出[17]：

式中：g（s，t）为像素灰度值；f^（x，y）为复原后的中心像素灰度值；Sxy为空间模板；mn为模板大小。

高斯函数由于其低通特性在滤波器中应用广泛，经过变换后也可变为高通滤波器，尤其是在双边滤波器和频率域滤波上，经常可以看到高斯滤波器的使用。低通的高斯滤波器用于对图像的平滑，而高通高斯滤波器用于锐化图像，本文研究高斯高通滤波器所具有的特性。频率域滤波中，理想的高通滤波器应具有如下特点[18]：

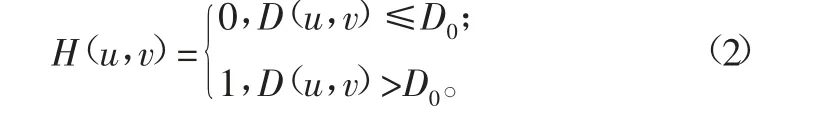
理想的高通滤波器理论上是可以实现的，但实际上本文使用的是特性相似的滤波函数来逼近理想的高通滤波，比如布特沃斯滤波器和高斯高通滤波器就在图像锐化中得到广泛应用，高斯高通滤波器可由下式来表达[18]：

图3所示的是形式变化后的高斯高通函数图像，常数c控制函数边坡的锐利度，函数值在γL和γH之间过渡。

图3 近似的高斯高通滤波函数特性

2.3 三维网格降噪方法

基于张量分解的三维网格降噪方法[7]主要通过模型几何属性获取子模型块相似块，对子模型块及其相似块的法向量进行张量处理。基于张量的网格降噪过程中，现有方法主要通过修正法向方向进行降噪，法向偏移没有进行优化处理。该方法的缺点是不能合理设置法向偏移量。

自适应双边滤波器网络滤波方 法[22]，结 合 三维网格模型的局部特征强度，自适应地优化滤波参数，实现局部双边滤波器中数值滤波器和空域滤波器的合理搭配。该滤波器能够更好地保持三维网格模型的细节特征。不过，自适应双边滤波器检测特征强度的复杂度较高。因此实现效率较低。

加权的M-估计器方法中[21]，虽然有效地保持模型的特征，但是该方法需要人为干预去调节参数，需要用户的经验值。

3 加权的几何均值滤波器

3.1 几何均值滤波器的推广

几何均值滤波器的操作对象是图像灰度值，即图像像素点具有的一个颜色属性。在网格数据中，能够表征网格点属性的量有很多，可以从PM中选取构造，设VM中的任意点可以表示为v=（vx，vy，vz），本文选取点空间位置作为网格滤波的基础，可以将几何均值滤波推广至三维空间，有下式：

式中：vi=（vix，viy，viz）是中心点；vj=（vjx，vjy，vjz）是vi的1-邻域点；N=N（vi，1）是邻域点个数；v^i=（v^ix，v^iy，v^iz）是迭代的新点位置。类似于灰度值零点的处理，在处理三维点空间位置时，也需要将网格点平移到第一卦限，保持v=（vx，vy，vz）的坐标值恒正，在滤波完成后再进行平移还原。

3.2 显著性（相似性）高斯权函数的构造

有关于特征区域的判别也是几何处理中的有趣的研究内容，噪声与网格的几何特征都属于高频信息，现在依然没有一个有效的数学定义将二者区分开，在网格的尺度很大的情况下，甚至连人眼都难以区分，所以目前在区分特征与噪声的研究上往往是拟合一个度量函数来迭代求解，或者是依据能量函数进行全局的优化迭代求解。在网格滤波算法发展的历程中，几乎所有方法的求解优化和函数拟合都有一个特征显著性或者相似性的度量函数[19]。目前在特征显著性度量上，可以用急剧变化的方向曲率及高斯曲率等作为度量阈值；也可以使用网格点法向量夹角、网格边夹角及三角片面夹角等，本文中则使用法向量夹角和空间距离来识别网格模型的显著特征，最后拟合一个函数进行新顶点位置的求解。

3.2.1 同态滤波思想应用

为了避免特征区域受到不同流型面的影响而被钝化，本滤波算法设计的基本思路是滤波器要具有能够将噪声点拉向原始曲面，以满足降噪要求，同时保持特征不被钝化的特点，参考1.3节介绍的同态滤波思想，综上所述，推广的新点迭代公式可以按如下重写为

式中：K（t，r）∈（0，1），是本算法的显著（相似）性度量函数；t、r变量均为表征特征的参数变量，参考式（2），滤波器关注于感兴趣的特征区域，特征的判别属于阈值控制，所以理想的显著性度量高斯权函数K（t，r）应该具有式（2）的特点，公式的中括号内容是同态滤波器的应用形式，用于保持（锐化）特征，整个点空间位置的迭代公式属于全局点空间位置的几何均值滤波函数，用于去除噪声（纹理特征）。

3.2.2 高斯核函数的应用

与算术均值中的加权双边滤波相似，点的法向量夹角γ和点的空间距离S作为本文显著性度量函数的基础，即t=γ，r=S，本文使用几何均值来计算两个特征显著性值，K（t，r）表达式为

式中：θv为法向量夹角的阈值；θs为空间距离的阈值；θv和θs都是自适应的，可以由模型网格点中的平均法向量夹角和平均边长计算得到；μ0、μ1为相关系数，即阈值控制系数，它控制着高斯权函数的边坡锐利度，控制系数是本文算法特征保持性能的关键，通常需要进行参数调整来确定最优的值，实施过程中依据经验选取，如对一些只包含平面和不连续特征的机械零件模型可以将μ0、μ1选取得小一点，以使滤波函数拥有更好的特征保持性。

3.3 算法步骤

表1给出了本文算法的伪代码。通过设置迭代次数，使得算法达到最好的降噪效果，同时保持关键特征，一般而言，iterations=3时本文算法能够在保持特征的同时进行噪声的去除，迭代过多就可能会模糊特征，针对不同模型进行试验选取合适的迭代次数可以得到更适合模型的效果。

表1 算法的伪代码

4 结果

本实验实施了章节2.3所讲述的算法，加性噪声水平为0.15，μ0、μ1分别设置为0.12和0.30，实验中对比了经典的最小平方滤波算法[20]、Susan结构保持滤波算法[5]、加权的M-估计器滤波算法[21]、特征保持的双边滤波算法及本文算法。

如图4所示，使用机械零件模型来验证本文的算法效果，从图中标记区域可以看出本文算法在特征保持上有着相当良好的效果，虽然特征保持的双边滤波算法也有着良好的特征保持效果，但是算法降噪后存在噪声点，降噪效果并不理想。如图5所示，本文使用Bunnies-iH模型来对比不同算法得到的效果，从灰色框标示的区域可以看出，非鲁棒性的最小平方滤波算法严重模糊了特征，同样的M-估计器和特征保持的双边滤波算法在眼睛和文字特征的保持上没有本文提出算法的效果好。

图4 Frandisk模型的不同算法降噪效果对比

图5 Bunnies-iH模型不同算法降噪效果对比

如图6所示，灰色框标示的区域中，特征保持的双边滤波算法在眼皮上仍然有未去除的噪声存在，本文算法、Susan降噪与加权的M-估计器均有着良好的降噪和特征保持效果；如图7所示，最小平方滤波虽然降噪效果很好，但是特征也被严重模糊，在左边灰色框标示的3D人像中，有3个比较大的噪声点存在，右边的灰色框标示区域中所标记的是头发特征，经过本文算法降噪只剩下2个噪声点，同时头发特征被很好地保留下来。

图6 Man-head模型不同算法降噪效果对比

图7 lenaH模型不同算法降噪效果对比

为了进一步证明本文算法在不同模型上良好滤波的性能，表2定量统计了4种算法与本文算法滤波完成后网格模型相较于原始无噪声网格模型的最大绝对误差Dmax、平均误差Dmean、误差方差δ及均方误差（MSE），加粗部分为最优结果。从表2可以看出，本文算法的误差统计值与均方误差（MSE）上都能取得最低值，这说明采用本文的方法能够最大程度地去除噪声、恢复原始模型并有效保持特征。图8对比了滤波的4种算法与本文算法在4种模型上的均方误差值，从均方误差（MSE）可以看出，与其他算法相比，本文算法在不同模型上的表现更稳定，误差也更小。

表2 滤波后相比原始模型的误差统计以及均方误差

图8 本文算法与其他算法在不同模型上均方误差的对比

5 结论

本文在几何均值滤波基础上，综合了同态滤波和双边滤波等的思想，并延伸至3D 网格滤波降噪中，实验表明该算法在特征保持和降噪上都有着良好的效果。算法的处理的核心是基于点空间位置的鲁棒统计，并应用类似于双边滤波中的权值的处理，算法中选取了法向量夹角值与空间距离作为权值，并构造了模型特征局部相似性高斯度量权函数。最后基于同态滤波的理论来设计迭代公式对顶点位置进行更新迭代。算法鲁棒性关键在于模型特征局部相似性权重函数的使用，即如果滤波的中心点在特征区域，迭代公式受到相似权函数的影响会执行锐化的操作，类似于图像锐化处理的高通滤波；如果中心点在非特征区域，迭代公式受到相似权函数的影响会执行平滑的操作，类似于图像降噪处理的低通滤波。算法的对比实验效果及定量的误差分析数据表明了本算法对具有不同特征尺度模型的降噪处理具有一定的效果。本文的不足在于：本文的算法只有针对非CAD模型具有好的降噪效果，但是针对CAD零件模型尖锐处没有达到很好的效果，并不能体现出本文算法的优势。在未来的工作中希望对该算法加以改进，使算法具有普适性。