基于黑底白圆标定板的面结构光标定算法优化

邱飞达，董静，熊新炎

（哈尔滨商业大学 轻工学院，哈尔滨 150028）

0 引言

目前信息技术不断发展，基于结构光的三维扫描技术已经兴起，其中，基于面结构光的三维扫描技术具有快速性、稳定性，且视场比较大，越来越受到三维重建技术方面的重视[1-2]。系统标定对系统至关重要[3]，在传统系统标定过程中， 由于相机和投影仪的装置或算法缺陷导致噪点及特征点相位识别不准确而影响标定结果，从而导致三维重建精度不高或失败。为满足实际三维重建所需的精度要求，面结构光三维重建系统的系统标定的优化对面结构光的实际应用具有重要意义。

基于面结构光三维重建系统中存在的以上问题，本文提出了一种基于黑底白圆标定板的面结构光系统标定的改进方法。应用黑底白圆标定板进行特征点位置提取，采用面结构光投影仪与相机构成的三维点云传感器对标定板多个位姿进行扫描，得到多个位姿标定板的特征点位置及相位值，同时进行相机标定与系统标定，并基于双线性插值对结果进行优化，并通过SVD算法进行系统参数拟合，并经过实验对双线性插值得到的相位结果进行可视化，并通过该标定板对得到的三维点云精度进行检测。

1 面结构光三维标定系统模型

面结构光三维测量系统标定的任务，就是要确定像素坐标到三维坐标之间的转变关系。可以得到每个像素坐标的绝对相位值，因此系统标定也就是求解像素坐标、绝对相位值与相机坐标系下的三维坐标之间的对应关系[4-6]。

1.1 相位解算

相位解算的目的是建立（m，n）与θ的线性关系，从而进行从二维坐标向三维坐标的转化，本文采用四步相移法进行单频率结构光下的相位主值的求解，采用时间相位解包裹的多频外差法进行解相位。根据文献[7]可知，若在理想情况下，投影出四步相移的光栅图像的光强分别为I1、I2、I3、I4，投影仪产生的结构光周期分别为T1、T2、T3。则该频率下图像上某一像素点（x，y）的相位主值φ（x，y）为

其中round表示就近取整，φ12可以通过两个相位作差来获得，φ12的计算公式为：

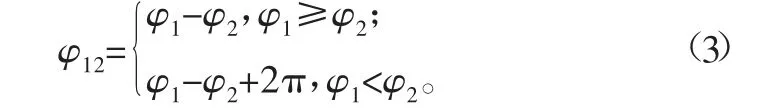
相位解算过程获取了像素坐标（m，n）与θ的对应关系。

1.2 针孔相机模型

比较典型相机标定方法有Tsai两步法[8]、张氏标定法[9]及分层逐步标定标定法等。经典的针孔摄像机模型[10-11]如图1所示。

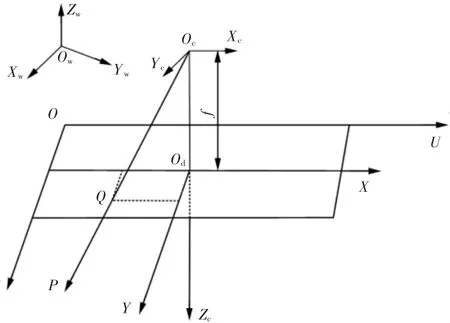
图1 经典的摄像机模型

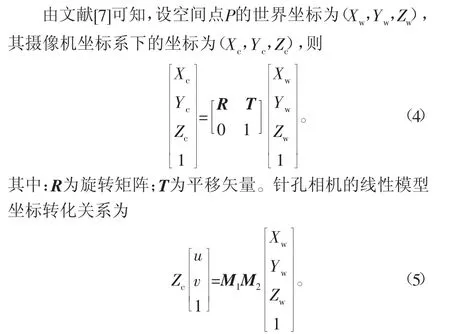
1.3 系统模型

面结构光投影仪的工作原理是：投影仪将正弦结构光以一定序列投射在物体表面，并通过摄像机同步采集，而后通过视觉算法对多副结构光图片进行解相位，并通过系统标定等技术得到的相位-像素-三维相机坐标的对应关系。根据文献[4]、[2]可知，在上述模型中由几何关系推导可知，二维像素坐标系下某一点的绝对相位θ与其在相机坐标系中的三维坐标（Xc，Yc，Zc）存在以下关系：

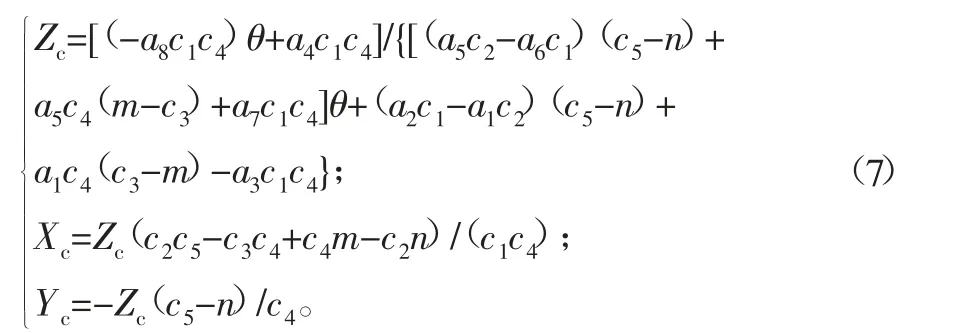
即可得到每个像素点对应的三维坐标，依次推入点云容器即可完成物体表面点云的三维重建。

2 基于黑底白圆标定板的系统标定

2.1 摄像机标定

由1.2节中分析已知，本文使用黑底白圆标定板进行摄像机的标定。圆心二维坐标由二维图像处理进行圆心拟合，再由标定板尺寸确认其世界坐标并构成一一对应关系。图2所示为其中一组位姿所采集的圆心提取结果及其局部放大图。

图2 圆心拟合结果

由标定板圆心提取拟合得到各特征点像素坐标（m，n），m、n为float类型。标定过程中，假设标定板放在世界坐标系中z=0的平面上，设定某一圆心的世界坐标为（0，0，0），各特征点的世界坐标（Xw，Yw，Zw）则由预设坐标系及标定板尺寸信息、圆心距等直接确定。若标定板位姿选取x组，每组特征点选取y个，即可建立x×y组的（m，n）和（Xw，Yw，Zw）的关系，并可以通过OpenCV、Matlab中的标定算法求得相机的内参数M1、外参数M2。

2.2 基于双线性插值的亚像素点相位拟合

由标定板圆心提取拟合得到各特征点像素坐标为亚像素点，我们可以得到整数点灰度值及相位值，但在亚像素点并没有像素值与相位值，故通过双线性插值的方式得到亚像素点相对较为精确的相位值。根据双线性插值原理，通过1.1节可以得到像素坐标（x，y）与相位θ的对应关系，设像素位置（x，y）处相位值为θxy。为得到亚像素点（m，n）的相位θmn的值，我们若已知其附近4个整像素点（m1，n1）、（m1，n2）、（m2，n1）、（m2，n2）的相位值θ11、θ12、θ21、θ22，则根据双线性插值原理，有：

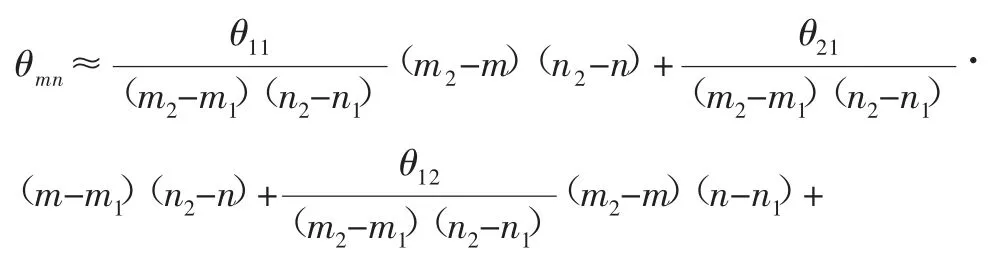
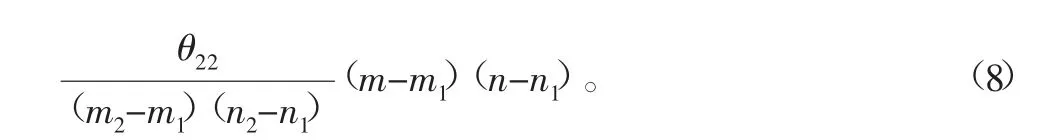
即可通过计算相邻整像素点的相位计算亚像素点的相位，能够提高特征点相位值的精度和提取稳定性。

2.3 基于SVD算法的系统参数拟合

由式（6），以a1～a8为待求解参量，可改写为

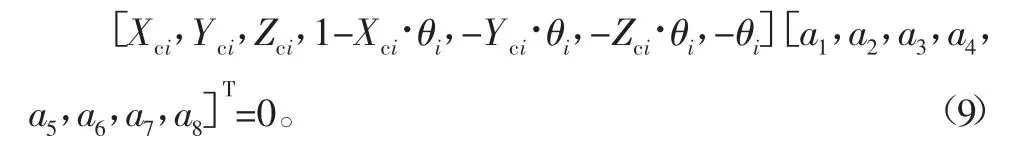
为使拟合结果和重建结果尽量准确，建立多组对应关系得到超定方程组，标定板变换次数尽量多，每组取适量点数进行标定，为三维重建做准备。由上述总结，其中左矩阵中参数均为已知量，目的在于拟合a1～a8的可能非零解。

考虑到式（9）所示齐次线性方程可以简化为Ax=0。其中，若A是方阵，由克莱姆法则可知，如果A是n×n的方阵而且r（A）=n，那么该方程组有唯一的零解；若A的行数大于列数，即A是超定方程组，这时实际上是没有真正的非零解析解的，因为约束太多了，没法都满足。但是可以求最小二乘解。求取最小二乘解的方法一般是使用SVD，即奇异值分解，由此即可解得a1、a2、a3、a4、a5、a6、a7、a8的一组非零拟合解，即完成系统标定，为三维点云求解奠定基础。

3 实验与结果分析

为了验证本文算法合理性，实验的硬件系统架构如图3所示。

图3 面结构光扫描系统实验台搭建

3.1 系统标定实验

本文所用的系统标定总体步骤如下：1）首先保持靶标不动，依次投射12种光栅模式图像与1张纯色光图像并使用摄像机进行采集；2）根据摄像机标定实验中的算法通过纯色光图像提取靶标上特征点坐标（mi，ni），实验中只取9点（标定板上3×3的圆心点阵），即i=0，1，……，8；3）根据2.2节所述相位拟合方法，通过双线性插值的方法求解亚像素特征点的相位值θi；4）移动标定板位置并使其处于投影仪与相机的公共视野内，重复步骤1）～步骤3）多次（一般取12～15次），通过特征点进行相机内外参的标定；5）通过标定得到相机的内参与每组标定板姿态下的外参，计算三维坐标（Xci，Yci，Zci）；6）将得到的所有组特征点信息（θi，Xci，Yci，Zci）代入式（10），组成超定方程组，根据2.3节中的分析，通过SVD算法求取系统参量a1～a8，即可通过该参量进行相机标定。

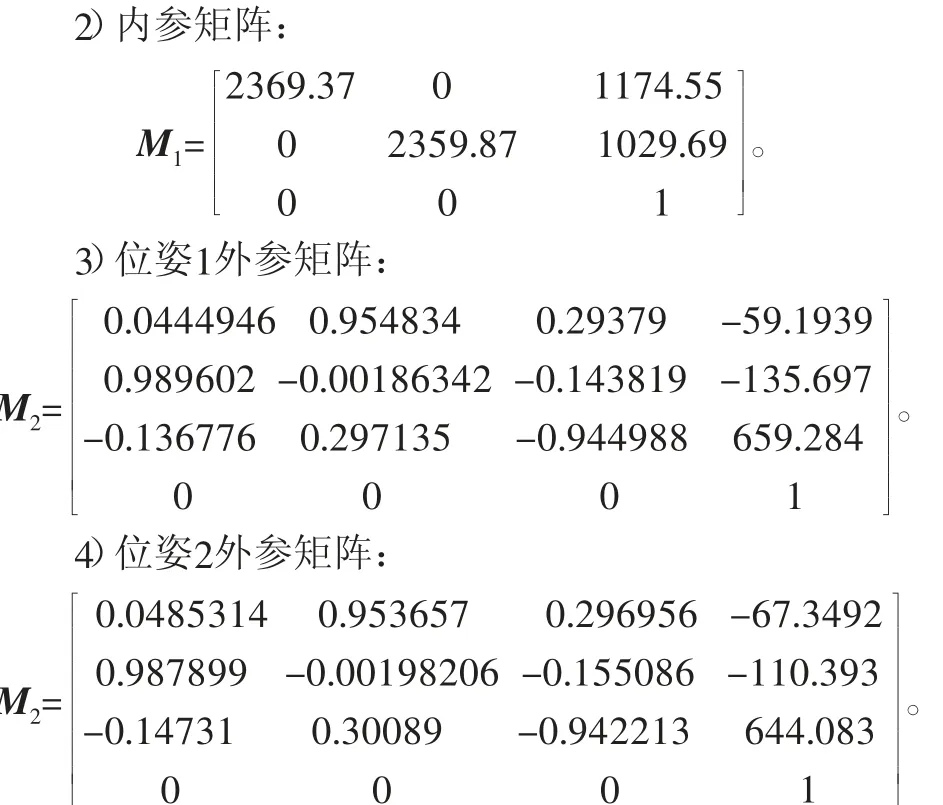
该组实验部分标定结果如下：

1）系统参数a1=-11.124，a2=0.28465，a3=-11.792，a4=4502.01，a5=0.0126304，a6=0.000706532，a7=-0.0313417，a8=1.0。

3.2 三维重建精度测试分析

面结构光测量技术受标定过程中非线性优化过程的限制，高度测量受相移偏差、系统非线性、源稳定性，以及在圆心拟合的过程中相机畸变导致的圆心不准确等因素的影响，会不可避免地存在误差[13-14]。在某一组实验中，在黑底白圆标靶二维图像中识别出圆心位置与重建出其三维坐标如图4、图5所示，实际距离与测量距离的部分误差结果如表1所示。

图4 二维圆心位置

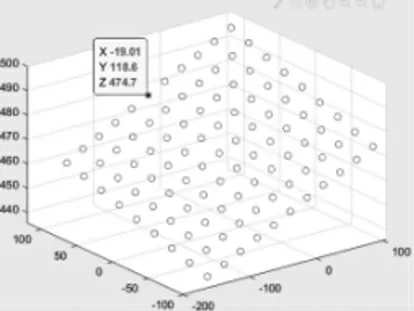
图5 重建的三维圆心位置

表1 部分测量结果与实际值的误差mm

通过多组实验验证，在本文选用的传感器工作距离与视场条件下，系统中重建误差平均为0.33 mm左右。由于本文的三维重建系统中平面点云间隔平均为0.22 mm，该系统标定算法的优化方法效果较好。

4 结论

1）本文提出了基于黑底白圆标定板的面结构光标定算法优化方法，通过双线性插值对基于黑底白圆标定板的面结构光系统标定进行了改进，并基于SVD算法对系统参数进行了拟合，得到一组可以使用的系统标定参量，为基于面结构光的三维重建提供了标定数据基础；2）通过大量实验表明，本文所提出的提取优化算法速度较快、稳定性较强、自动化程度较高，具有更强的抗干扰能力，拟合特征点相位及拟合系统参数的精度更高；3）本文提出的提取方法对环境光要求较为严格且对图像质量的要求较高，曝光过高或过低容易出现圆心提取失败或噪声过大导致的相位拟合失败，还有待进一步研究。