考虑钢筋锈蚀的混凝土材料劣化仿真
2022-06-21吴子涵
吴子涵,殷 鸣,刘 智
(1.江西省水利科学院,江西 南昌 330029;2. 南昌工程学院,江西 南昌 330099;3. 长江勘测规划设计研究有限责任公司,湖北 武汉 430010)
钢筋混凝土是水利工程建设的重要材料,然而长期处于干湿交替的工作环境导致钢筋极易出现锈蚀现象,是当前钢筋混凝土结构耐久性失效的重要原因。钢筋锈蚀会造成钢筋力学性能的削弱,与此同时钢筋与混凝土之间将出现一层锈蚀产物,影响钢筋混凝土之间的黏结滑移性能,并产生锈胀力增大混凝土保护层的内拉应力,致使结构发生锈胀破坏。当前学者关于钢筋锈蚀的研究主要集中于,试验提取锈蚀对钢筋混凝土材料力学性能的变化或基于非均匀分布理论的非均匀锈胀作用的研究等[1-5],少有将两者结合起来探究钢筋锈蚀对结构的影响,并缺少相应的理论仿真方法。为此,本文在已有钢筋混凝土分离式模型和混凝土损伤模型的基础上,结合钢筋锈蚀对钢筋混凝土材料性能的影响,重点分析钢筋锈蚀产生的锈胀作用以及对梁构件抗弯性能的影响,为后续进一步研究钢筋锈蚀对水工钢筋混凝土结构安全的影响提供理论基础。
1 钢筋锈蚀的影响
根据已有理论及试验研究,当前可将钢筋锈蚀对钢筋混凝土材料性能的影响分为3个方面。
1.1 钢筋锈蚀对钢筋力学性能的影响
钢筋锈蚀后,材料表面将逐渐出现大小不一的锈坑,从而降低钢筋自身强度及其变形能力。当前国内外学者的研究成果中,锈蚀引起的钢筋力学参数变化趋势基本一致,但受限于试验本身的复杂性与结果的离散性,锈蚀率与力学性能变化的定量关系差异较大,尚未出现较为统一的结论。本文采用吴庆等[1]的试验结果,将锈蚀率为5%作为模型的界限;该结论在CECS 220:2007《混凝土结构耐久性评定标准》[6]中也有体现,标准认为当钢筋锈蚀率达到5%时,构件已经属于严重锈损构件,因此本文仅研究锈蚀率ρ小于5%的情况。
fy,c=fy0(1-0.029ρ)
fu,c=fu0(1-0.026ρ)
δs,c=δs0(1-0.0575ρ)
εy,c=εy0(1-0.0575ρ)
Eu,c=Eu0(1-0.052ρ)
(1)
式中,Eu,c、fy,c、fu,c、δs,c、εy,c分别为锈蚀钢筋的名义弹性模量、名义屈服强度、名义极限强度、名义伸长率和极限应变;Eu0、fy0、fu0、δs0、εy0分别为未锈蚀钢筋的弹性模量、屈服强度、极限强度、名义伸长率和极限应变。
1.2 钢筋锈蚀对钢筋混凝土粘结滑移性能的影响
钢筋锈蚀后将在锈蚀表面产生一层零碎的锈蚀产物,此时受损混凝土与钢筋锈蚀产物将在材料的胶结部位形成新的粘结界面,该界面的力学性能受混凝土强度、保护层厚度以及锈蚀产物厚度等多方面因素的影响。本文钢筋锈蚀后钢筋混凝土极限粘结强度采用曾宇[2]论文中的试验拟合结果,其研究发现,常规分析模型与试验结果相差较大的原因是未考虑钢筋锈蚀率与各影响因素间的耦合效应,因此其建立的公式包含了与锈蚀产物厚度、保护层厚度和抗拉强度之间的关系,即
τcu=βuτou=K1K2K3τou
(2)
式中,τcu为钢筋锈蚀后材料极限粘结强度;βu为材料极限粘结强度折减系数;τou为材料原始极限粘结强度;K1为钢筋锈蚀产物厚度t的影响参数;K2为相对保护层厚度c/d的影响参数;K3为混凝土抗拉强度的影响参数。
根据其试验拟合,可得
K1=-0.058 7t+0.011 3
K2=-0.404 1(c/d)2+2.673 4(c/d)+0.252 6
K3=0.352 6ft+2.984 7
(3)
式中,t可根据GB/T 51355—2019《既有混凝土结构耐久性评定标准》[7]5.2.1节中公式求得。
钢筋锈蚀后的钢筋混凝土粘结强度折减系数则采用徐善华[8]论文中根据滕智明试验结果回归拟合的公式
β=1+0.562 5ρ-0.337 5ρ2+0.055 625ρ3-0.003ρ4
(4)
式中,ρ为钢筋锈蚀率;β为锈后钢筋与混凝土之间的粘结强度降低系数。
1.3 锈胀作用
通过数值模拟分析钢筋锈胀作用能够得到混凝土应力分布状态和裂缝潜在发展路径等试验难以获取的成果。当前学者们采用有限元法对锈胀作用的模拟主要有施加径向力,施加径向位移和设置温度膨胀环等3种方式[9]。无论采用何种方法模拟,均需要充分考虑锈蚀非均匀的基本特性,即实际工程中钢筋毗邻保护层的一侧总是先发生锈蚀,且锈蚀速度也远高于钢筋内侧。其中,施加径向位移的方法相对而言使用较为广泛[3],本文采用殷鸣[9]论文中引用的锈蚀钢筋周围混凝土径向位移非均匀分布模型,如图1所示。
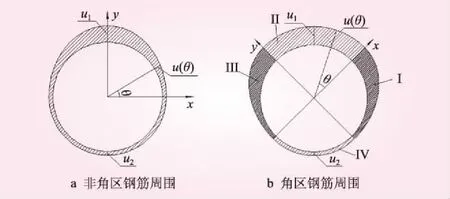
图1 混凝土径向位移分布
非角区钢筋周围混凝土径向位移分布规律为

(5)
角区钢筋周围混凝土径向位移分布规律为
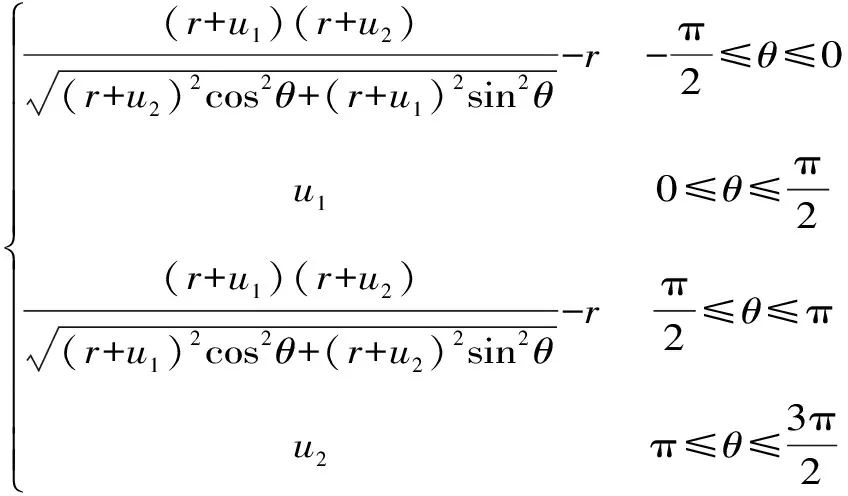
(6)
式中,r为钢筋半径;u1为外侧最大位移;u2为内侧最小位移;θ为各部位与x轴的夹角。
2 钢筋混凝土材料仿真分析模型
2.1 钢筋混凝土分离式模型
当前主流的钢筋混凝土材料有限元仿真分析模型主要可分为嵌入式模型、分布式模型和分离式模型,其中嵌入式模型和分布式模型假定钢筋与混凝土之间不产生相对滑移,主观消除了钢筋位移自由度的运算,因此虽然计算效率较高,但无法准确反映钢筋混凝土的相互作用。本文基于赵兰浩等[10]建立的单弹簧联结单元法,结合GB 50010—2010《混凝土结构设计规范》[11]所采用的徐有邻五段线模型构建钢筋混凝土分离式模型来模拟钢筋与混凝土之间的相互作用[12]。
单弹簧联结单元法如图2所示。该方法基于混合坐标系建立,采用实体单元模拟混凝土,使用杆单元模拟钢筋,并在混凝土与钢筋接触部位设置重复节点分别作为混凝土与钢筋插值点,建立弹簧单元作为两者间的联结单元。通过法向约束强制混凝土单元与钢筋单元间的法向自由度协同,通过设置切向弹簧模拟两者之间的切向作用,切向刚度则通过粘结-滑移本构关系确定,其有限元平衡方程为

图2 单弹簧联结单元法求解示意
(7)

正确的钢筋混凝土粘结-滑移本构模型是准确模拟钢筋混凝土结构性态的重要前提,本文采用的徐有邻五段线模型可分为胶结阶段、强度上升阶段、强度峰值阶段、强度退化阶段和摩擦稳定阶段(见图3),与钢筋混凝土相互作用机理吻合。其相应计算公式为
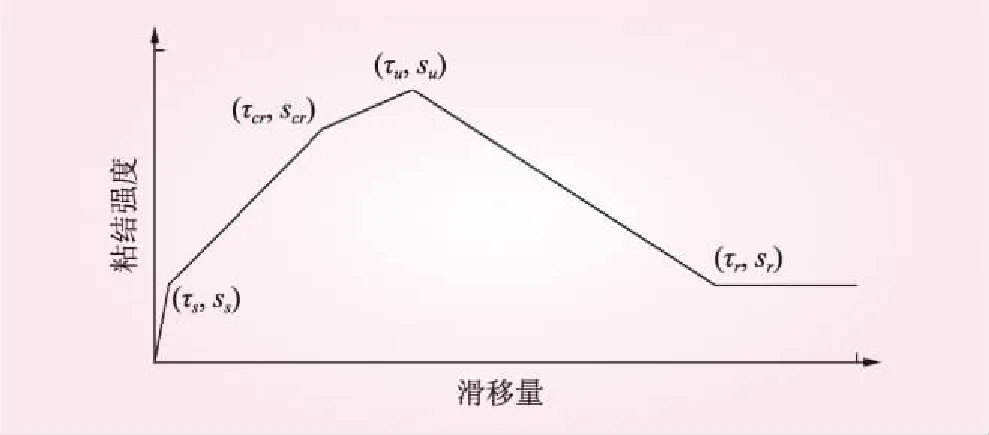
图3 钢筋混凝土粘结-滑移本构关系示意
(8)
式中,τ,τs,τcr,τu,τr分别为粘结应力及各阶段粘结强度特征值;s,ss,scr,su,sr分别为相对滑移量及各阶段滑移量特征值;k1,k2,k3,k4分别为胶着段、上升段、峰值段、退化段的斜率。
模型骨架线各阶段粘结强度与滑移量特征值见表1。

表1 钢筋混凝土粘结-滑移骨架线粘结强度与滑移量特征值
2.2 混凝土损伤模型
本文采用韦未等[13]基于四参数破坏准则的基本思路提出的四参数等效应变计算方法,通过式(10)的等效应变求解可将真实空间中复杂的多轴问题转化为等效空间中简单的单轴问题。
(9)
(10)
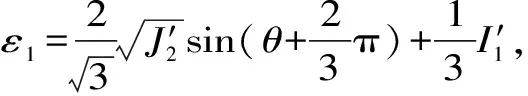
本文损伤模型选取过镇海提出的受拉与受压应力应变全曲线,该曲线已得到国内外科研工作者的认可,并纳入我国混凝土结构设计规范[11]。
混凝土单轴受拉应力应变曲线表达式为
σ=(1-dt)Ecε
(11)
(12)
(13)
式中,σ和ε分别为混凝土的应力与应变;ft,r为混凝土单轴抗拉强度;εt,r为ft,r对应的应变;dt为单轴受拉损伤变量;Ec为混凝土弹性模量;at为混凝土受拉应力应变曲线软化段参数。
混凝土单轴受压应力应变曲线表达式为
σ=(1-dc)Ecε
(14)
(15)
(16)
(17)
式中,fc,r为混凝土单轴抗压强度;εc,r为fc,r对应的应变;dc为单轴受压损伤变量;ac为混凝土受压应力应变曲线软化段参数。
当结构处于多轴状态时,需用等效应力应变σ*和ε*替代真实应力应变和ε,通过应变张量第一不变量I′1判断单元拉压状态,该模型正确性已在文献[14]中得以验证。
3 算例验证
3.1 锈胀作用算例
截取文献[15]中梁试件的横截面建立二维有限元模型,如图4所示。模型尺寸为100 mm×160 mm,在布置钢筋处设立与钢筋截面相对应的孔洞,保护层厚15 mm。本算例仅考虑梁底部的受拉钢筋和顶部的受压钢筋的锈胀作用。

图4 梁试件二维模型示意(单位:mm)
本算例材料参数如表2所示,推求损伤模型四参数取值为:A=0.013 47,B=0.131 49,C=0.742,D=0.245 19。本文锈胀加载取角区最大径向位移u1为15 μm,u1/u2=30,将模型钢筋孔洞处各节点位移线性逐步增大,以模拟锈胀的过程。

表2 算例材料参数
根据混凝土损伤演化发展,整个锈胀过程大致可分为4个阶段,如图5所示。从图5可知:①内裂期。锈蚀发生后将首先在面向角区方向出现开裂,形成3条明显的损伤演化路径,此时钢筋附近混凝土将不断发生应力重分布,内部随钢筋锈胀发展沿损伤路径持续演化。②扩展期。随着锈蚀产物不断增加,混凝土损伤沿初始路径向外部发展,此时4个角区部位的混凝土损伤沿两条相互垂直路径迅速演化,主拉应力区不断向外部转移,混凝土保护层外表面同时出现受拉破坏并向内部延申。③贯通期。随着锈蚀程度进一步增加,混凝土内部裂缝与外部裂缝形成贯通,此时裂缝贯通路径上的应力完全释放转移,混凝土表层出现脱落。由于上部钢筋直径较下部钢筋偏小,因此上部区域的混凝土保护层出现损伤贯通较下部更迟。④深化期。虽然混凝土保护层已形成贯穿裂缝,但锈胀作用仍随锈蚀程度加深而继续,此时混凝土损伤程度不断加深,混凝土表层脱落现象加剧,同时裂缝逐步向内部发展。

图5 锈胀作用演化发展过程
3.2 四点弯曲梁算例
选取Walraven四点弯曲梁试验作为研究对象,研究不同锈蚀率对受弯梁试件的影响。模型如图6所示。模型尺寸为4.1 m×0.2 m×0.45 m,在底部40 mm处布置3根不同直径钢筋;模型顶部施加对称的分级荷载,在右侧支点施加法向约束,左侧支

图6 四点弯曲梁试验模型示意(单位:mm)
点施加双向约束。模型混凝土材料参数如表3所示。

表3 算例材料参数
对受弯梁构件处于锈蚀率0~5%之间的6种情况进行计算,计算工况如表4所示。

表4 算例材料参数
计算所得梁试件的损伤演化过程如图7所示,由于各工况下损伤演化过程相似,因此仅列演化过程的示意图。由图7可见,其过程与常规试验规律一致。不同锈蚀率下梁试件的荷载-扰度曲线如图8所示。由图8可见,在各种锈蚀率下,混凝土梁开裂前的荷载-挠度关系均呈线性变化,各工况下数值基本一致。当梁在跨中底部出现开裂现象后,荷载-挠度曲线斜率较开裂前减小,此时不同锈蚀率的荷载-挠度曲线存在较为明显的区别,底部钢筋锈蚀导致粘结滑移曲线中的化学胶着段消失,极限粘结强度也有所降低,因此梁的抗弯能力将随着锈蚀率增大而明显降低。

图7 四点弯曲梁试件损伤演化过程

图8 不同锈蚀率下梁跨中荷载-挠度曲线对比
对于梁受弯构件数值仿真而言,通常计算的极限荷载会略低于试验数据,主要原因有:①试验结果受试验条件和试验过程影响,存在一定的离散性;②试验推求的材料本构模型未能充分考虑钢筋的强化阶段;③数值计算中所考虑的不均匀锈蚀与真实情况存在偏差,全截面锈蚀相较真实情况更为严重,导致结果偏大。
4 结 语
本文针对钢筋混凝土结构无法规避的钢筋锈蚀问题,梳理了钢筋锈蚀对钢筋混凝土材料性能的影响因素,并根据相关研究成果筛选出可靠的影响因素数值计算方法。结合已有的钢筋混凝土分离式模型和混凝土损伤模型,通过算例分析钢筋锈蚀后的锈胀作用以及对混凝土受弯构件抗弯性能的影响。计算结果能够较为准确地描述钢筋锈蚀后钢筋混凝土材料性能的变化,为进一步研究钢筋锈蚀对水工钢筋混凝土结构安全的影响奠定了良好基础。
