新安江模型参数线性化率定研究
2022-06-21王红艳王新龙
王红艳,王新龙,周 倩,杨 宇
(1.宁波弘泰水利信息科技有限公司,浙江 宁波 315000;2.宁波市水利水电规划设计研究院有限公司,浙江 宁波 315000;3.江苏省水文水资源勘测局徐州分局,江苏 徐州 221000)
0 引 言
流域水文模型在进行水文规律研究和解决实际生产问题中起着重要作用。中国现在最常用的流域水文模型是新安江模型[1],模型结构考虑了湿润半湿润地区的蒸散发、产汇流特性。采用新安江模型建立实际流域的洪水预报方案时,首先要根据流域的实际水文资料对新安江模型参数进行率定,然后根据率定的参数制定洪水预报方案,对未来的洪水进行预报[2]。
流域水文模型除了模型结构要合理外,模型参数的率定也是一个十分重要的环节[3],模型参数的好坏直接关系着洪水预报方案的优劣。传统的参数率定方法为人机交互率定,其主要根据人们的先验知识进行判断、估计。这种方法虽然简单易行,但调试参数需要大量时间且得到的参数不一定是最优的[4]。目前,国内外研究较多的是模型参数自动率定方法,参数的自动率定就是人们预先编制好一个参数自动寻优的计算程序,然后输入水文资料和模型参数初始值,通过自动寻优计算得到最优的模型参数值[5-7]。
传统上的参数优化的方法是数学寻优法,几乎都是以误差平方和最小为目标函数,在目标函数响应曲面上寻找参数最优值,通过一阶函数求导为零得到参数的最优值。这种方法对于线性参数具有较好的效果,但是用于优选非线性参数时,会给非线性参数增加不相关的局部优值。为了避免在非线性参数优选时出现这些问题,包为民教授提出了非线性函数参数的线性化率定方法[8],在函数响应曲面上寻找参数的最优值。本文把参数线性化方法应用于新安江模型,并通过理想流域和实际流域验证该方法的可行性和高效性。
1 新安江模型参数线性化率定方法
1.1 新安江模型介绍
赵人俊教授于1973年在编制新安江入库洪水预报方案时提出了新安江模型。新安江模型结构是分散性的,主要分为蒸散发计算、产流计算、分水源计算、和汇流计算四个层次。模型各层次结构的功能,计算采用的方法和参数见表1。

表1 新安江模型各层次结构功能、计算方法和相应参数
1.2 新安江模型参数线性率定原理
参数线性化率定方法对非线性参数函数以参数作为自变量求导,再通过导函数差分线性化,并对线性化的参数用误差平方和目标函数进行率定,然后逐步逼近非线性参数的最优值。该方法收敛、率定速度快,解决了以误差平方和为目标函数求解非线性函数参数增加不相关的局部优值的问题。与传统的方法相比,该方法的实用性更强、效果更好。
新安江模型结构完整,计算清晰,是一个典型的非线性模型。把新安江模型看作一个非线性函数,模型的计算流量当作该函数的因变量,模型的参数当成该函数的自变量。首先,对新安江模型参数变量求导,通过导函数差分使参数线性化;然后,把新安江模型这个非线性函数进行一阶泰勒级数展开,构建计算流量和模型参数之间的线性函数,通过最小二乘法求解参数。把非线性参数函数转变为线性参数函数求解可以避免产生一些不相关的局部参数解。以流量误差平方和、参数迭代步长收敛容差为目标函数进行率定,逐步逼近新安江模型参数全局最优值。
1.3 新安江模型参数线性率定步骤
把新安江模型这个非线性函数进行多元一阶泰勒级数展开,构建计算流量q(θ,x)和模型参数θ之间的线性函数

(1)
式中,q(θj,x)=[q(θj,x1),q(θj,x2),…,q(θj,xL)]T为L组函数计算值,即根据新安江模型参数θj和水文资料系列x计算的防洪断面流量过程q(θj+1,x)=[q(θj+1,x1),q(θj+1,x2),…,q(θj+1,xL)]T,L组真参数相应的函数值,如果模型没有任何误差,其值为实测的断面流量系列,后面计算时用实测流量系列代入;θj=[(θ1,j,θ2,j,…,θn,j)]T为函数的参数变量,即新安江模型的参数变量;x=(x1,x2,…,xL)T为函数的输入变量,即实测的雨量、蒸发等水文资料;e=(e1,e2,…,eL)T为函数的误差,即模型的误差。
具体率定步骤:
(1)根据参数的物理意义和流域的实际情况给定一组新安江模型参数初始值θ0。
(2)根据给定的参数向量、降雨资料、蒸发资料用新安江模型计算防洪断面流量q(θ,x)和参数灵敏度矩阵[5]S,S反映了参数改变引起计算流量的改变程度。把S代入函数式(1)得函数式(2),计算S时需要计算函数对各参数的偏导数,通过导函数差分使参数线性化,计算公式见(式3)、(式4)。如下
q(θj+1,x)=q(θj,x)+S(θj+1-θj)+e
(2)
(3)
Δθi,j=0.001θi,j
(4)
(5)
(3)用最小二乘法[6]求解式(2),得到新的参数向量Qj+1和参数寻找方向Δθ。即
θj+1=θj+(STS)-1ST(q(θj+1,x)-q(θj,x))
(6)
Δθ=Qj+1-Qj
(7)
(4)以流量误差平方和最小为目标函数确定参数寻找方向上最优步长比例系数b(1≥b>0),得出寻找方向上最优的参数向量θj+1。即
(8)
θj+1=θj+b(STS)-1ST(q(θj+1,x)-q(θj,b,x))
(9)
(5)判断新的参数θj+1与上一步参数θj之差是否小于给定的迭代步长收敛容差ε,即|θj+1-θj|<ε,如果小于则寻优结束,得到最优参数θj+1;否则,令θj=θj+1转步骤(2)继续循环计算,直到得到满足条件的最优参数。
要证明步骤(3)中寻找方向的正确性,只要证明对于任意一步寻找的参数向量θj+1对应的流量误差平方和Fj+1比上一步参数向量θj对应的流量误差平方和Fj小即可。证明如下[7]
Fj+1=(q-qj+1)T(q-qj+1)
(10)
Fj+1=
[q-qj-bS(θj+1-θj)]T[q-qj-bS(θj+1-θj)]=
Fj-b(q-qj)TS(θj+1-θj)-b(θj+1-θj)TST(q-qj)+
b2(θj+1-θjTSTS(θj+1-θj)
(11)
把式(6)代入式(11)得
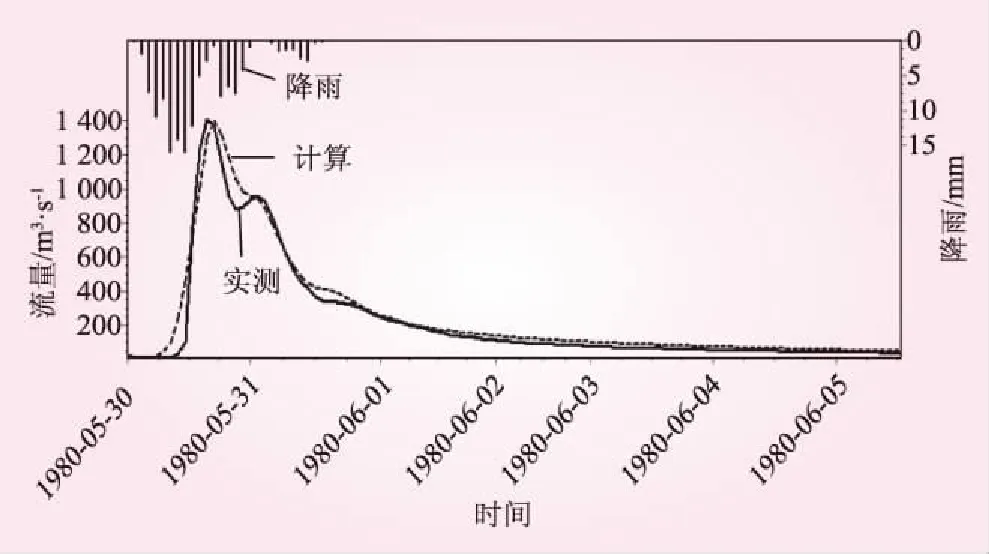
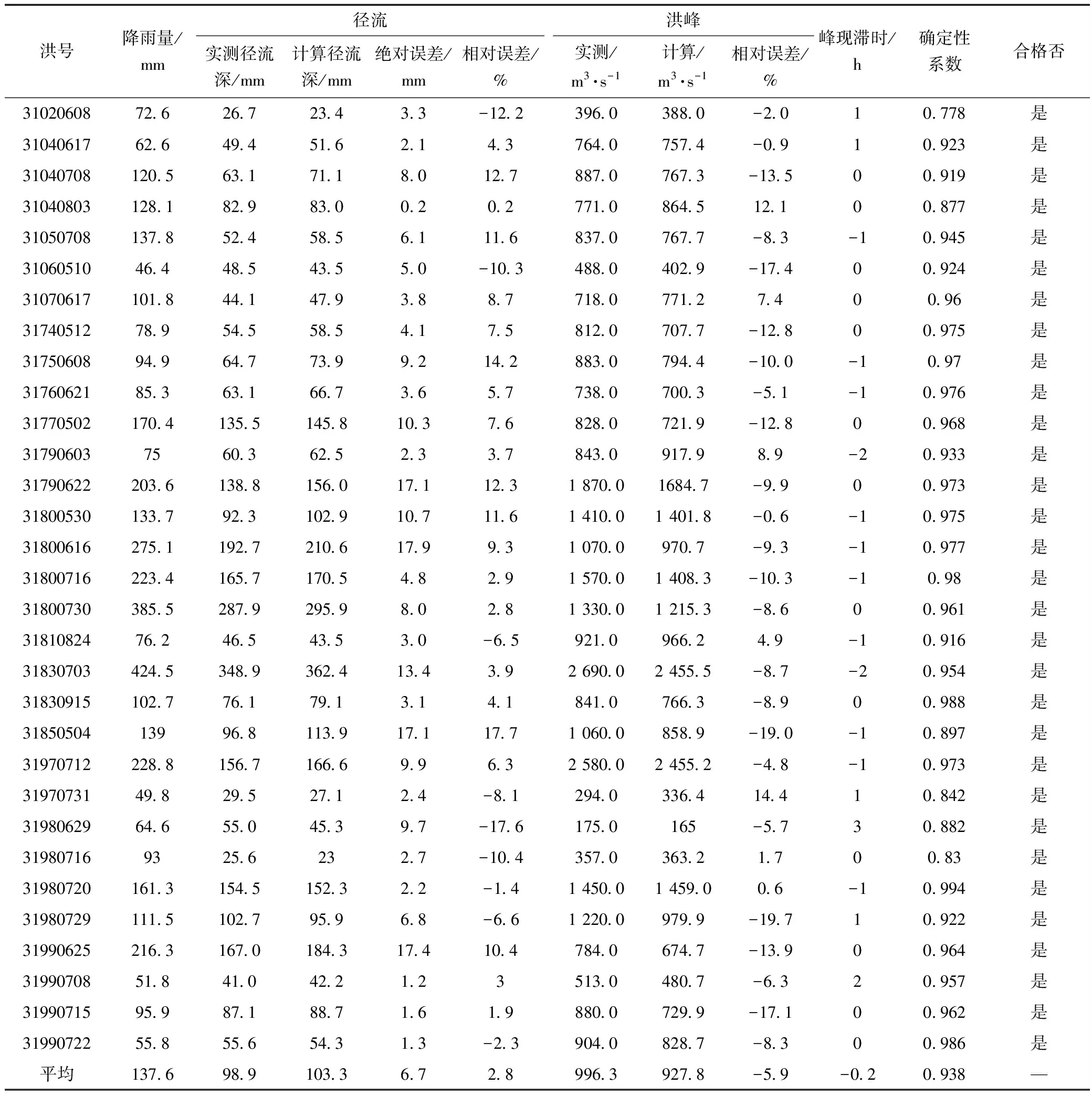
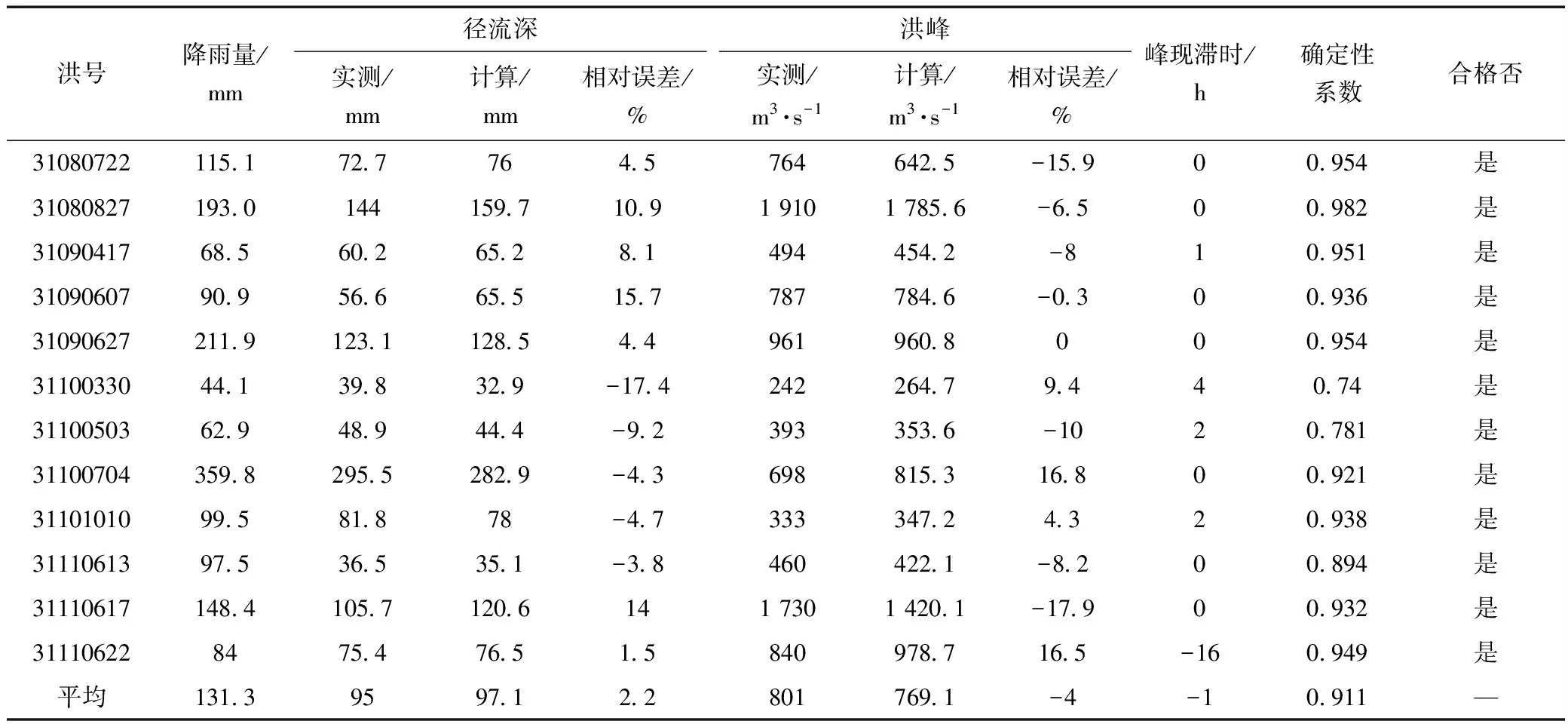
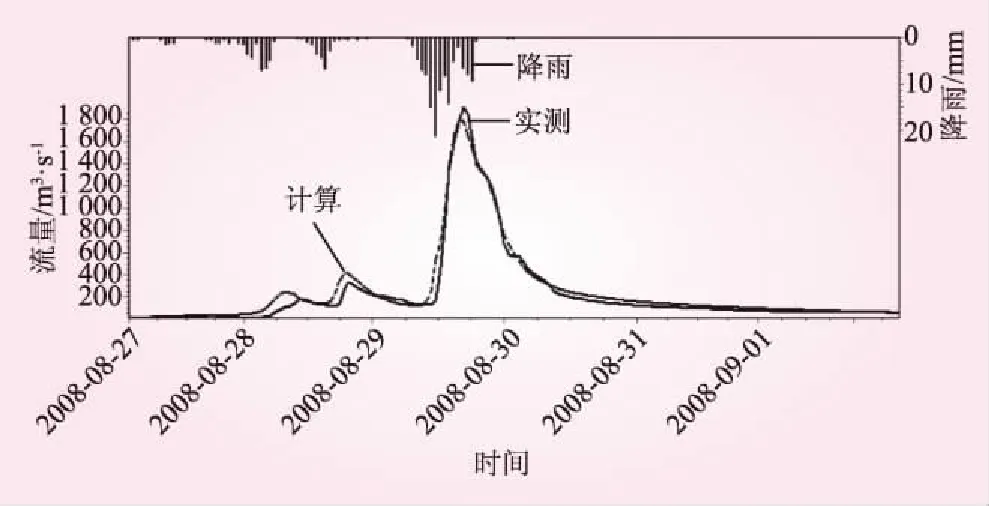
Fj+1=Fj-2(q-qj)TS(STS)-1ST(q-qj)+ (12) 由此可见,参数率定过程中的流量误差平方和是递减的。随着循环计算次数的增加,其对应的流量误差平方和越来越小,最终趋向于最小值,参数也逐渐逼近最优的参数值。 在模型参数的优选中,目标函数的选取直接影响参数率定的效率和结果。本文根据对模型成果的要求,选择的子目标函数主要有5个。 (1)计算流量和实测流量的误差平方和 (13) 式中,Qx为计算的流量值,m3/s;Q0为实测流量值,m3/s。 (2)迭代步长收敛容差ε,反映参数率定过程中同一个参数相邻两个计算值之间的距离,用来判别参数率定过程是否结束的条件,若同一个参数相邻的两步计算值之间的距离小于ε,则认为率定的参数值已收敛到最优值附近。 (3)径流深的相对误差 (14) 式中,Rc(i)为计算径流深,mm;Ro(i)为实测径流深,mm。 (4)洪峰的相对误差 (15) 式中,Qmax,c为计算洪峰,m3/s;Qmax,o为实测洪峰,m3/s。 (5)确定性系数DC,主要用来评价洪水预报过程和实测流量过程之间的拟合程度,确定性系数越大,表明计算流量和实测流量过程拟合得越好。即 (16) 选取福建东张流域作为理想流域,用给定的一组新安江模型参数值,即参数真值(表2)、实际蒸发资料、实际雨量资料计算流域出口断面的流量过程,把该流量过程作为理想实测流量。然后根据这些水文资料进行新安江模型参数线性化率定,如果率定的参数结果能够回到参数真值,则说明新安江模型参数线性化率定方法合理有效,可以把该方法用于实际流域,进一步研究该方法的实际应用效果。 表2 参数初值取值范围 针对新安江模型SM、KI、KG、CS、CI、CG、KE、XE统一进行新安江模型线性率定,检验该方法在高维数的参数空间的应用效果。具体的率定步骤如下: (1)在参数的物理意义范围内随机给SM、KI、KG、CS、CI、CG、KE、XE赋初值,各参数取值范围如表2。 (2)根据不同的参数初值分别进行新安江模型参数线性化率定,SM、KI、KG、CS、CI、CG、KE、XE的迭代步长容差均取0.000 1,即当率定过程中SM、KI、KG、CS、CI、CG、KE、XE同时满足迭代容差要求时率定结束。 (3)计算结果见表3。从表3可以发现,SM、KI、KG、CS、CI、CG、KE、XE取不同初始值,经过新安江模型参数线性率定方法均可以回到真值附近。参数率定过程中平均率定次数为83次,平均最终流量误差平方和从2 786 117.38(m3/s)2下降到112(m3/s)2,参数和误差平方和的收敛速度非常快,率定效果很好。 表3 理想模型率定结果 洈水流域地跨湖北省、湖南省,流域面积954.2 km2,属亚热带过渡性季风气候区。乌溪沟水文站位于洈水水库中上游,由于该水文站以上的子流域受人类活动影响较小,流域资料的可靠性性、一致性、代表性比较好。 本次选取乌溪沟1974年~2011年43场洪水过程作为次洪资料。其中,1974年~2007年的31场洪水资料作为率定期资料,2008年~2011年12场洪水资料作为检验期资料。 用新安江模型参数线性化率定方法对乌溪沟流域的次洪模型分水源参数(SM、KI、KG)、坡面汇流参数(CS、CI、CG)、河道汇流参数(KE、XE)进行统一率定,率定步骤和结果如下: (1)在给定范围内随机给上述赋初值(见表4),分别随机取20组参数初值进行计算,且保持KI+KG=0.7。 表4 参数初值范围 (2)根据不同的参数初值分别进行参数线性化率定,各参数的迭代步长收敛容差均取0.001,即当以上各参数同时满足迭代步长容差时,率定结束。 (3)参数率定结果见表5。从表中可以发现,各参数取不同初始值,经过新安江模型参数线性率定方法均可以收敛到固定的优值附近,这些参数优值均在其物理范围内。参数平均率定次数为163次,收敛速度很快,效果很好。次洪率定最终参数见表6。 表5 乌溪沟流域参数率定成果 表6 乌溪沟流域次洪参数 (4)次洪模拟结果见表7,31场洪水参与模拟全部合格,合格率达到了100%。平均实测径流深为98.9 mm,平均计算径流深为103.3 mm,径流深平均相对误差为2.8%。平均实测洪峰为996.3 m3/s,平均计算洪峰为927.8 m3/s,平均洪峰相对误差为-5.9%,平均峰现时差提前0.2 h,平均确定性系数为0.938。其中,2次洪水模拟过程见图1、2。 图1 31830703次洪水模拟过程 图2 31800530次洪水模拟过程 表7 乌溪沟流域次洪参数率定选取2008年~2011年之间12场洪水作为检验洪水,计算结果见表8,12场洪水全部合格,合格率为100%。其中,2次洪水模拟过程见图3、4。 表8 次洪检验结果 图3 31080827次洪水模拟过程 综合评定表明,31场洪水参与模拟,全部合格,合格率为100%;12场洪水参与检验,全部合格,合格率为100%,平均确定性系数为0.923。根据GB/T 22482—2008《水文情报预报规范》,预报等级为甲等。 图4 31090627次洪水模拟 本文把包为民教授提出的参数线性化率定方法应用于新安江模型,建立了新安江模型参数线性化率定方法,并通过理想流域应用和实际流域应用验证了该方法的的可行性和高效性。该方法具有以下优点: (1)新安江模型参数线性化率定方法在模型函数曲面上求解参数,解决了在流量误差平方和目标函数曲面上求解参数时增加不相关的局部优值的问题。 (2)新安江模型参数线性化率定方法用一阶泰勒级数函数以参数作为自变量展开,用最小二乘法确定参数的寻找方向,用参数迭代步长收敛容差和流量误差平方作为目标函数,寻找路径始终在目标函数曲面的低值槽附近,寻找过程的路径短,最终找到的参数为参数的全局最优值。 (3)新安江模型参数线性化率定中参数的收敛速度快,不受参数空间维数和参数初始值的影响,参数率定结果稳定。取不同个数、不同的初始值的参数组合,经过线性化率定均可以较快地收敛到稳定的参数最优值附近。 综上所述,新安江模型参数线性化率定方法合理有效,计算思路简单明确,具有较好的实际应用效果。
(q-qj)TS(STS)-1ST(q-qj)=
Fj-(q-qj)TS(STS)-1ST(q-qj)1.4 新安江模型参数线性率定指标
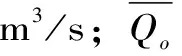
2 理想流域验证


3 实际案例应用
3.1 乌溪沟流域次洪参数线性化率定




3.2 乌溪沟流域次洪模型检验

4 总 结
