基于原位力学测试的织物折皱回复性表征

胡霄睿， 孙丰鑫， 肖彩勤， 高卫东

(1. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122； 2. 江南大学 设计学院， 江苏 无锡 214122)

织物作为一种典型的纤维集合体软材料[1]，其在低应力作用下便可产生复杂的多尺度结构调整、材料黏弹塑性与滞弹响应协同作用下的屈曲折皱效应，并直接影响织物的外观和市场价值。因此织物折皱回复性的表征和调控是纺织领域面临的基本问题之一[2]。

现行的织物折皱回复性测试方法包括折皱回复角法和外观平整度法[3-4]。随着计算机技术的进步，许多研究者在结合上述二类方法基础上，将图像技术引入到织物折皱回复性的评价中，包括用动态图像检测织物折皱回复角度[5]，构建织物折皱外观的表观特征图像[6]，以及通过双目机器视觉等方法重构织物表面三维折皱形貌等[7]。图像技术的运用使得织物折皱回复性评价的客观性有了很大提升。然而，织物折皱回复角测试过程中由于织物自由端的扭转和卷曲等现象，往往带来较大的测量误差；而现有外观平整度的图像检测很难克服织物复杂纹理和花型对评价结果的干扰，同时需要复杂耗时的织物起皱处理过程，造成织物性能提升和产品创新的诸多障碍。

近来许多研究通过织物力学性能和折皱回复角相关性分析，说明了织物折皱回复性能与物理性质的必然联系[8-9]。织物折皱回复性作为不同外力作用下的织物本征物理性质的宏观表现[10]，其力学表征具有潜在的优势。对此，本文针对织物黏弹响应的高时间依赖性特征，提出了时间、空间上连续(原位)的织物保形性力学测试方法，并解析测试曲线及特征指标的物理意义，通过与折皱回复角的相关性分析，阐明力学方法在织物折皱回复性测试中的潜在应用价值。

1 实 验

1.1 试样准备

从鲁泰纺织股份有限公司和江苏阳光集团有限公司分别选取棉型织物和毛型织物，挑选代表性的抗皱性能不同的19种机织物，均为经过染整的成品织物，原料主要涉及棉、棉/涤和毛/涤,具体规格参数如表1所示。

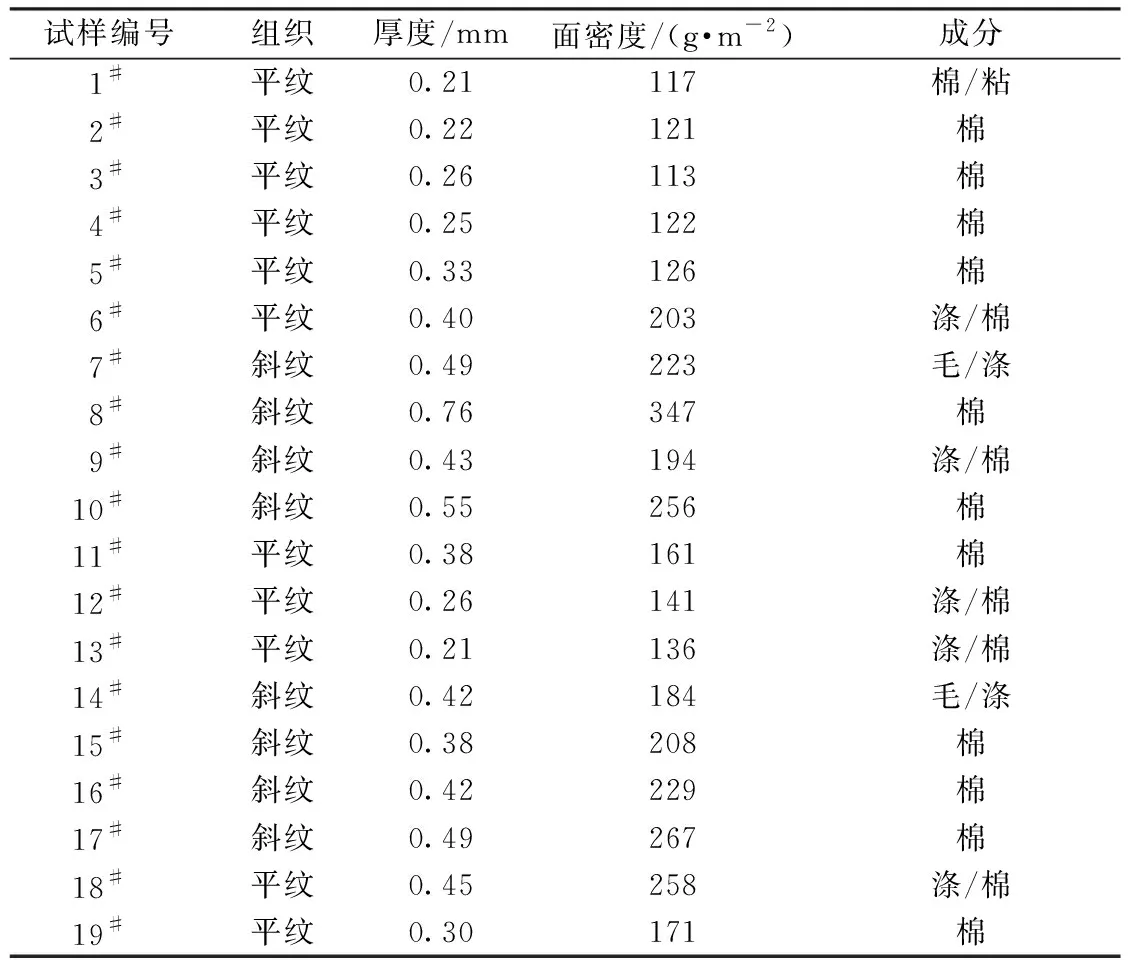
表1 织物基本规格参数Tab.1 Primary parameters of fabrics

1.2 折皱回复性的力学测试

1.2.1 测试装置

为实施织物折皱回复性的力学测试，设计了织物保形性原位力学测试系统如图1所示，主要包括移动板、测试板、力传感器、伺服电动机以及相应的数据采集和处理系统[11]。织物通过移动板和测试板上的夹持器夹持于两板之间，并呈倒八字形略微悬垂状态，以保证测试过程中织物弯曲屈曲的稳定性。移动板在伺服电动机驱动下相对测试板进行往复运动，从而构造织物的多重形变状态；同时力传感器实时采集织物组合变形下的复合力值，输出相应的力-位移测试曲线。

图1 织物保形性原位力学测试系统示意图Fig.1 Schematic of shape retention in-situ evaluation system for fabrics

1.2.2 测试原理

原位力学测试方法可实现在时间和空间上对织物材料的连续测试，称之为原位，同时区别于现有折皱回复角等通过角度测量或视觉图像的测试手段而称之为力学测试。根据织物的典型变形特征可将测试过程分为弯曲屈曲阶段Ⅰ、压缩阶段Ⅱ、折皱回复阶段Ⅲ、伸直阶段Ⅳ、拉伸阶段Ⅴ、拉伸回复阶段Ⅵ等6个测试阶段(见图2)。测试中，移动板在伺服电动机驱动下向靠近测试板一侧运动，织物在测试板和移动板作用下产生弯曲屈曲变形，即I弯曲屈曲阶段；直到弯折的织物两翼相互接触，随着移动板继续靠近测试板对织物施加压缩载荷，进行Ⅱ压缩阶段测试。移动板在压缩力到达设定的最大值时停止对织物继续加载，然后移动板反向远离测试板运动，使夹持于测试板和移动板之间的织物压缩和屈曲变形逐渐回复，此时对应Ⅲ折皱回复阶段。直到织物逐渐由弯曲状态变为伸直状态后，移动板继续远离测试板，使得织物由伸直状态开始产生伸长变形，直到力传感器监测到力值到达设定的最大拉伸力，完成V拉伸阶段测试，最后移动板由拉伸位置反向靠近测试板直至运动到测试初始位置结束，完成VI拉伸回复阶段测试。

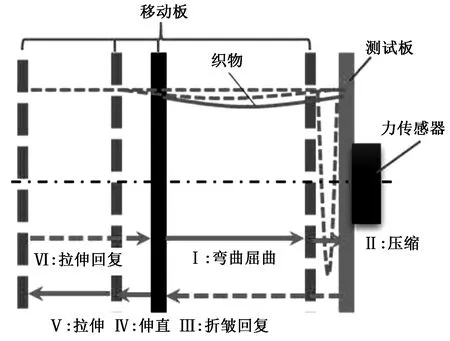
图2 原位力学测试过程与主要特征阶段Fig.2 In-situ mechanical testing process and featured testing steps

通过构造织物弯曲屈曲、压缩、压缩和屈曲回复、拉伸以及拉伸回复等组合变形，同步监测织物变形过程中的黏弹塑性力学响应，采集相应的测试力值获得力-位移曲线，对织物的保形性进行综合表征。

1.2.3 实验参数设置

原位力学测试中，实验参数设置为：测试板和移动板的隔距为10 mm，最大压缩力和最大拉伸力均为300 cN，移动板回复停滞时间为30 s，移动板运动速度为20 mm/min，力值的采样频率为80 Hz[12]。所有织物试样压平后裁剪为长×宽为30 mm×20 mm， 放置于标准大气((20±2)℃，湿度(65±3)%)下平衡24 h以上。每种织物备注3块试样进行测试，取平均值作为测试结果。

1.3 折皱回复角法测试

参照AATCC 66—2006《机织物折皱回复性的测定:回复角法》，利用SDL-M003型折皱回复角测试仪，对标准大气((20±2) ℃，湿度(65±3)%)下的织物折皱回复角(AWR)进行测试。考虑到织物折皱回复性的各向异性，为方便力学测试与折皱回复角测试结果的对比分析，2种方法均对织物经向进行测试。

2 结果与讨论

2.1 测试曲线分析与指标提取

织物原位力学测试典型的力—位移曲线如图3所示。根据测试的特征阶段，测试曲线也对应6个过程。本文主要基于织物折皱回复阶段曲线分析，探讨织物的折皱回复性的力学表征方法。在折皱回复阶段，随着弯折织物的缓慢回复，纵坐标轴负方向曲线对应的力绝对值逐渐下降到0 cN(如图3测试曲线与横坐标轴的交点A所示)，然后又从0 cN 逐渐增大以克服织物黏塑响应引起的残余变形；换言之，原位力学测试过程中，当移动板运动到对应于测试曲线的A点时，测试板和移动板对织物水平方向没有外力作用，此时类似于织物自由回复状态。因此，交点A与坐标原点O的偏移量Dfr与织物折皱后的自然回复角度具有内在关联，可提取为织物折皱回复性的一个特征指标。随后力值继续增大，织物因其固有的滞弹性而在移动板作用下开始被动回复过程，曲线与纵坐标轴相交于点B，对应的力值Fwr反映了折皱诱导的残余力，也可用于织物折皱回复性表征。此外，由于织物弯曲滞后性与其折皱回复性间存在密切关联[13]，可由标度律[14]表达为：

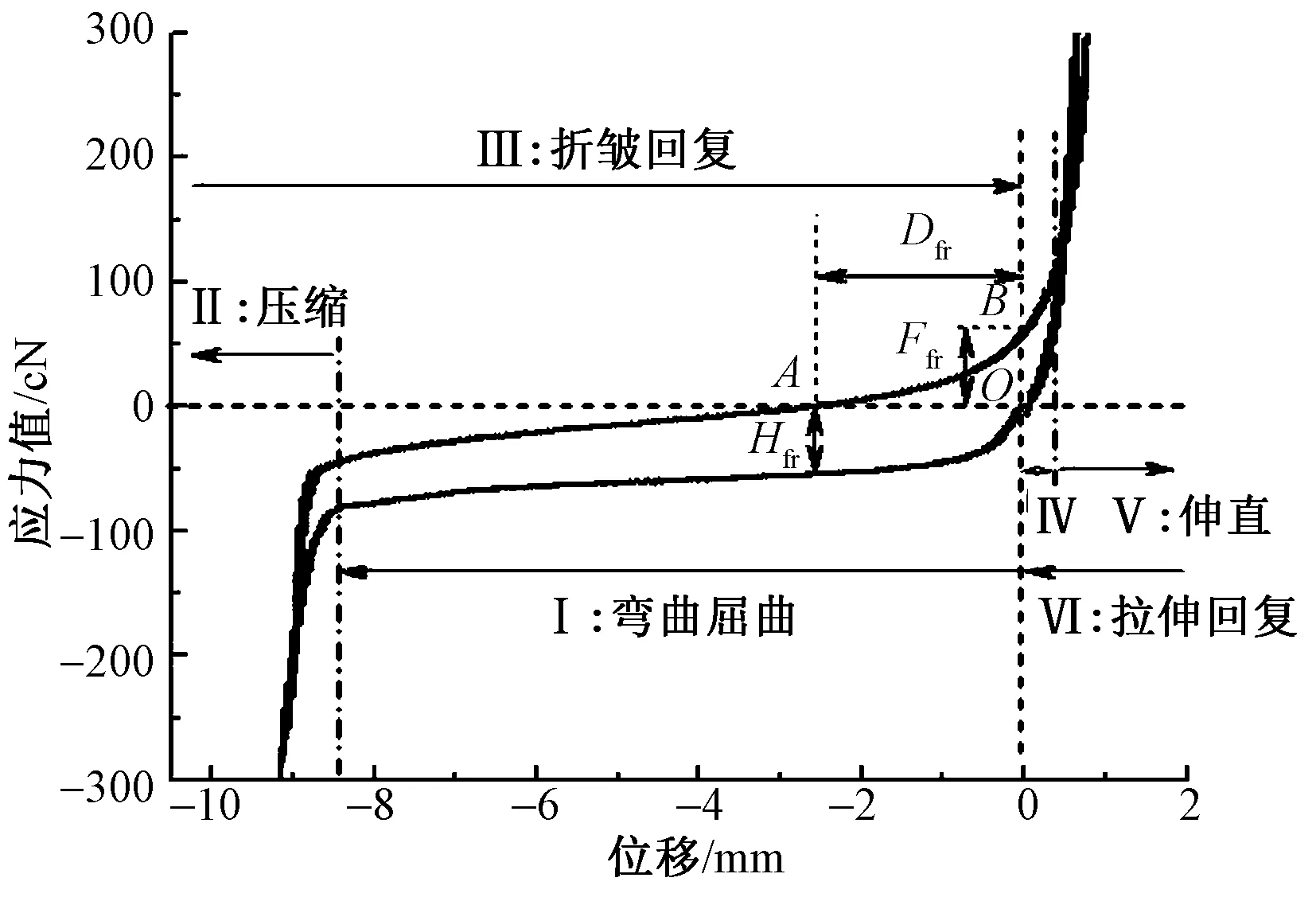
图3 原位力学测试系统典型的力-位移曲线Fig.3 Typical force displacement curve of in-situ mechanical tests

Bhm～αn

(1)

式中：Bhm为弯曲滞后矩；α为 折皱回复角；n为幂指数。因此，弯曲屈曲阶段曲线与折皱回复阶段的滞回曲线间的滞后矩Hfr也反映了织物折皱回复特性。

原位力学测试曲线的折皱特征指标(偏移量Dfr、折皱诱导的残余力Fwr以及滞后矩Hfr)以及对应织物折皱回复角测试结果，如表2所示。表中数据均为织物纵向3次测试结果的平均值，则3次测试曲线的折皱特征指标变异系数CVD、CVF和CVH以及折皱回复角AWR的变异系数CVA计算结果如图4 所示。从图中数据可见，原位力学测试方法获得的折皱特征指标的变异系数均低于0.10，而折皱回复角法所测的折皱回复角数据波动性略大，特别是4#、12#和15#织物，测试结果稳定性较低，折皱回复角的变异系数大于0.16。因此从测试数据总体来看，原位力学测试方法的稳定性好于折皱回复角法。主要原因为：折皱回复角法测试中，织物自由翼的卷曲和扭转会引起读数误差，而且将织物从压缩块下取出转移到角度测试盘的过程存在一定人为干预误差。原位力学测试方法，织物在夹持状态下进行力学测试，直接测试织物的折皱回复性能，避免了织物折皱回复角的读取过程，没有织物扭转等因素的干扰，而且基于高精度力传感器的力学测试方法避免了图像测试中的随机性，具有可重复性高、精确可靠的优势。

表2 折皱特征指标与织物折皱回复角测试结果Tab.2 Results of feature indices and wrinkle recovery angles

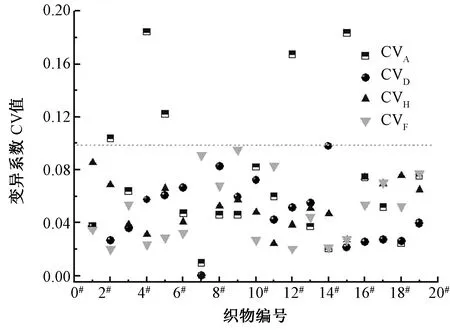
图4 折皱特征指标和折皱回复角CV值比较Fig.4 Comparisons of coefficients of variation between feature indices and wrinkle recovery angles

2.2 折皱特征指标与折皱回复角关系

表3示出原位力学测试的折皱特征指标与折皱回复角的Pearson相关系数。可见，3个折皱特征指标均与折皱回复角在0.01水平具有显著的相关性，说明原位力学测试获得的折皱特征指标与折皱回复角具有必然关联，可以用来表征织物的折皱回复性。其中偏移量Dfr与折皱回复角相关系数最大，进一步验证了该指标的物理意义：原位力学测试中对测试力值为0 cN时的织物回复偏移量与折皱回复角法所测织物自由翼的自由回复状态时候的折皱回复角度之间的对应关系。

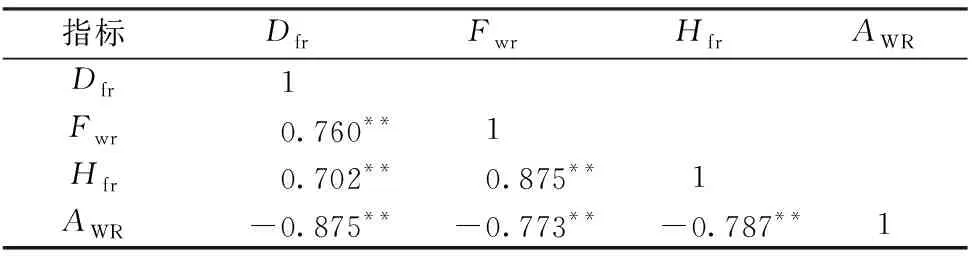
表3 折皱特征指标与折皱回复角的相关性分析Tab.3 Correlation analysis of feature indices and wrinkle recovery angles

为进一步分析3个指标与折皱回复角的相互关系，以折皱特征指标作为自变量，以折皱回复角作为因变量，采用逐步回归法，p<0.05和p>0.10分别作为自变量进入和剔除回归方程的标准，构建多元线性回归方程，如式(2)所示：

(2)

从式(2)可见，偏移量Dfr和滞后矩Hfr被纳入回归方程，而基于方差分析在95%概率下没有将折皱诱导的残余力Fwr纳入回归方程。这主要是由于折皱诱导的残余力Fwr指标反映了织物从折皱状态回复到自由状态后再被拉伸而展平所需要的额外作用力，此过程是折皱回复角所不能反映的。因此Fwr指标没被纳入折皱回复角的回归方程。然而此指标作为评价织物折皱回复性的有效指标，可以更好反映织物折皱回复到原始状态整个过程的回复性能，具有重要意义。从这一点来看，原位力学测试方法提供了比折皱回复角更为丰富的评价指标，更能全面反映织物的折皱回复性能，且上述回归模型及其构建方法有望应用于织物折皱回复角的高效、客观评价。

3 结 论

本文提出织物折皱回复性的原位力学测试方法，通过解析力-位移测试曲线，提取偏移量、折皱诱导的残余力和滞后矩3个折皱特征指标；结合折皱回复角和折皱特征指标的变异系数对比分析，说明力学测试方法稳定性和可靠性好于折皱回复角法。采用逐步多元回归和Pearson相关系数对折皱特征指标与折皱回复角相关性进行了分析，表明力学测试曲线提取的折皱特征指标与折皱回复角在0.01水平具有显著相关性，可以用来表征织物的折皱回复性，且原位力学测试方法提供了比折皱回复角更丰富的评价指标，因此能全面、客观表征织物折皱回复性能。