借图识数巧解题

文／李苏萍

在大数据时代，通过统计与分析，我们可以推断所测对象的本质，甚至预测对象的未来。对于收集来的数据，我们可以根据问题直接分析，也可以将数据绘制成统计图帮助分析。很多同学习惯利用数字和公式，通过计算来解决问题，忽视统计图的作用。其实，统计图上的数据已经按照需求进行了处理，可直观地反映出数据的集中趋势和离散程度。如果我们能借助统计图的特征，多角度观察与分析，就可以提高解题速度。

一、借图看数据的集中程度

例1某射击运动员在赛前训练中射击了10次，成绩如图1所示。下列结论中错误的是（ ）。

图1

A.众数是8 B.中位数是8

C.平均数是8.2 D.方差是1.6

【解析】本题是用折线统计图反映该运动员的成绩。很多同学将图像信息转化成一个个数据9，6，8，8，7，10，7，9，8，10，再计算众数、中位数、平均数和方差。由于没有充分利用统计图的特征，解题效率不高。因为本题是用点来反映数据的集中与离散程度的，所以我们可以换个方式看此图。众数可以通过每一行数据表示的点的个数得出，如图2，数据6 有1 个、7 有2 个、8 有3 个、9 有2 个、10 有2 个，很容易看出众数是8。找中位数需排序，而该图本身有排序的功能，所以只需从下到上给点排序（如图3），不难看出中位数是排第5 位和第6 位两个数的平均数，即（8+8）÷2=8。我们从图4 中发现，点反映的数据集中在8 附近，所以平均数8+A、B、C 三个选项都可由图轻松得出是正确的，故选D。

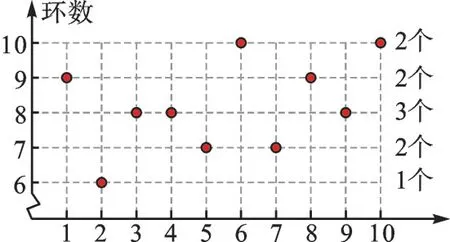
图2

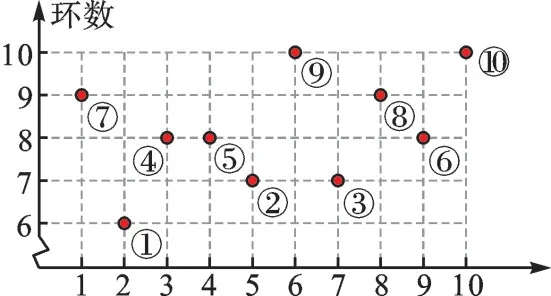
图3

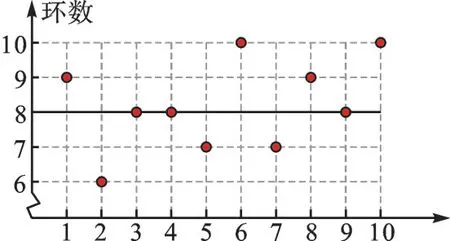
图4

例2学校为了解全校学生参加社会实践活动的情况，随机调查了部分学生一学期参加社会实践活动的时间（单位：天），并用得到的数据绘制了统计图5和图6。请根据图中提供的信息，回答下列问题：

图6

（1）本次随机调查的学生人数是______，图5中m的值是______；

图5

（2）求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数；

（3）该校有480 名学生，根据获取的社会实践活动时间样本数据，估计该校一学期社会实践活动时间大于10天的学生人数。

【解析】本题两幅统计图反映的内容是一样的，只是表现方式不同，我们可以根据统计图的特征选择适合的图回答相应的问题。

问题（1）中，学生人数和m的值可分别根据条形统计图和扇形统计图直接计算得到。本次随机调查的学生人数是4+12+10+8+6=40（人），m%=1-10%-30%-25%-15%=20%。

问题（2）中，观察图6，根据条形的高度看出数据10 出现12 次，所以众数是10。计算中位数需要排序和找中间位置，两幅图都有一定的排序功能，中间位置是排在一半附近的数据，所以选择扇形统计图找到排在50%的数据更容易。观察图5，从小到大排序，实践9 天与10 天的人数百分比之和为40%，再加上11 天的人数百分比为65%，所以中位数为。本题的平均数是加权平均数，选择扇形统计图可直接计算，x=9×10%+10×30%+11×25%+12×20%+13×15%=11，即平均数是11。

问题（3）中，选择能反映各项与总量之间关系的扇形统计图更合适。在这组样本数据中，社会实践活动时间大于10 天的学生人数占60%，所以估计该校一学期社会实践活动时间大于10 天的学生人数为480×60%=288（人）。

【点评】折线统计图中点的高低起伏、条形统计图中条形的长短、扇形统计图中扇形面积的大小都可以反映数据的分布和变化特征。因此，我们应抓住问题的本质，巧借图形本身的特征，以达到快速解题的目的。

二、借图看数据的离散程度

例3图7 为本溪、辽阳6 月1 日至5 日最低气温的折线统计图，由此可知本溪、辽阳两地这5天最低气温波动情况是（ ）。

图7

A.本溪波动大

B.辽阳波动大

C.本溪、辽阳波动一样

D.无法比较

【解析】能反映气温波动情况的数据是极差和方差。因此，这里我们的常规解法是分别计算两组数据的方差进行比较即可判断，但这种方法耗时耗力。如果用统计图来观察两地气温的波动情况，不难看出，将虚线向上平移，会和实线重合，也就表明了两地气温的波动是一样的。故选C。

例4在市运动会射击比赛选拔赛中，某校射击队甲、乙、丙、丁四名队员的10 次射击成绩如图8 所示。他们的平均成绩均是9.0环，若选一名射击成绩稳定的队员参加比赛，最合适的人选是（ ）。

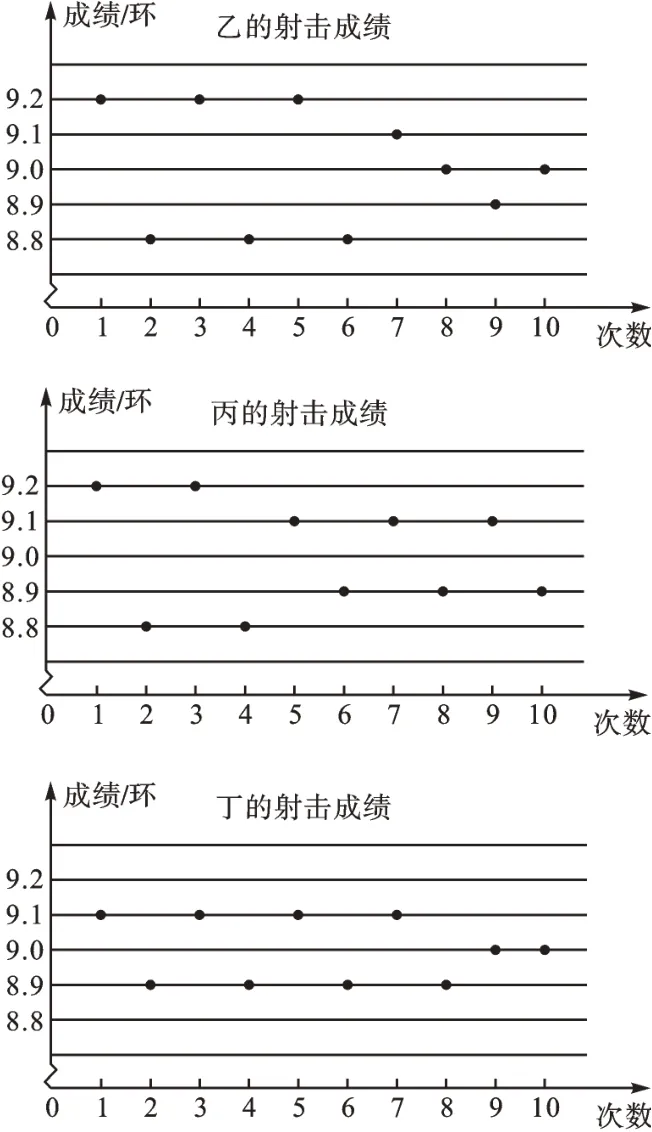
图8

A.甲 B.乙 C.丙 D.丁

【解析】解题的关键词是“稳定”，即用方差来反映各组数据的离散程度，但直接通过计算来求4 个队员成绩的方差，运算量较大，不太合适。方差在统计图上还反映每个点相对于平均数上下波动的幅度。那么，我们通过观察4 幅统计图，发现乙和丙的成绩波动较大，甲和丁的成绩波动较小。再将甲和丁两个成绩统计图重合对比，又可感知丁的成绩波动更小。故选D。

【点评】例3 和例4 都是考查数据的离散程度。通过计算方差来看数据的波动情况自然精确，但比较耗时；如果用统计图来看数据的离散程度，特别是当波动情况明显一致或差别较大时，往往能轻松得出结论。