注重答题规范，方可“颗粒归仓”

文／于婷婷

你是否曾有过这样的经历：明明全都会做，感觉胜券在握，结果却被扣了分。如果你仔细推敲自己的答题过程，就会发现：答题过程“对而不全，全而不美”。所谓“对而不全”是指方法正确，结果或过程不完整；所谓“全而不美”是指答题混乱，没有逻辑性和条理性。如何克服这种现象，力求得分“颗粒归仓”呢?下面，老师结合一个案例告诉你两个小窍门。

例如图1，在苏州工业园区的金鸡湖东岸，有一座水上摩天轮“苏州之眼”，其直径为120m，旋转1 周用时24min。小明从摩天轮的底部（与地面相距0.5m）出发开始观光。摩天轮转动1 周，小明何时处于离地面90.5m的空中？

图1

我们先来看某同学的解题过程：因为旋转1 周用时24min，所以摩天轮旋转的速度为360÷24=15°/min。作如图2 所示的辅助线。因为OB=60m，AB=0.5m，AH=90.5m，所以OH=30m。在Rt△OPH中，因为OP=60m，OH=30m，所以∠P=30°，∠POH=60°。同理∠QOH=60°，所以OB转到OQ、OP的度数为120°、240°，120÷15=8min 或240÷15=16min。

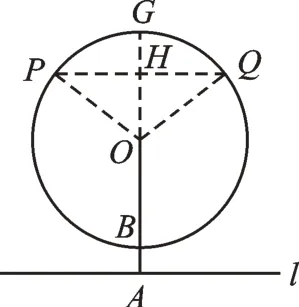
图2

窍门一：规范答题，结构完整

应用题一定要做到有问必答，而这名同学只是算了两个时间就结束了。不清楚地标明所解的内容，阅卷老师怎么知道这就是问题的答案呢？另外，作辅助线是一种主观性较强的行为，若不“指名道姓”，仅用一句“作如图所示的辅助线”来阐述作图方法是无法让阅卷老师看明白的，甚至会让阅卷老师曲解你的解题思路。因此，本题需要交代清楚OG、OP、OQ、PQ这四条线段是如何作出来的以及它们的交点是如何形成的。

我们建议如此订正：将“作如图2 所示的辅助线”改为“延长AO交圆于点G，过OG的中点H作PQ⊥AG，从左至右分别交圆于点P和点Q，连接PO、PQ、OQ”。同时，在过程的最后补上“答：摩天轮转动一周，小明在8min 或16min 时处于离地面90.5m 的空中”。

【点评】我们要规范解题过程和答题格式，只有表述科学、严谨才能避免无谓的失分。

窍门二：逻辑连贯，合理踩点

在经过第一轮“对而不全”的改进之后，解题规范虽然得到了优化，答题结构也更加完整，但有些细节的处理还不到位，整体逻辑也不够连贯，可谓“全而不美”。例如本题中小明所处的位置应该是P、Q两点，但该同学只指出点H与地面的距离是90.5m，并没有说清楚点H与点P、Q之间的关系，直接默认点P、Q到地面的距离也为90.5m，在推理的逻辑线上少了一环，使得整个过程缺乏条理性。另外，在Rt△OPH中，根据OP与OH的长推导出∠POH与∠P的角度，最好以三角函数作为过渡，否则显得较为唐突。

我们建议如此订正：增添证明点P、Q到地面的距离是90.5m。因为PQ⊥AH，l⊥AH，所以PQ∥l，又因为平行线之间的距离处处相等，所以点P、Q到l的距离等于点H到l的距离，即90.5m。在证明∠POH=60°时，我们可以这样描述：在Rt△POH中，因为OH=30m，OP=60m，所 以cos ∠POH=所以∠POH=60°。

【点评】若将一道题比作一条“项链”，那么每一个思维节点则是串成这条项链的“珍珠”，只有逻辑连贯，有条理地思考、研究与表达，才能串起更多的“珍珠”，让得分“颗粒归仓”。