巧建坐标系 妙解几何题——与笛卡尔的“时空对话”

文／ 周 炼

相传法国哲学家、数学家笛卡尔有一天卧病在床，正思考着如何将几何与代数相结合，此时一只蜘蛛在墙角来回移动。笛卡尔突发奇想，将蜘蛛看成一个点，墙角的线看成数轴，坐标系的雏形便应运而生，代数与几何之间也架起了一座桥梁。那么，老师想问问同学们，当你们遇到几何问题时，会从代数角度去思考吗？今天我们不妨也将“点”视为“蜘蛛”，看看能否打开研究几何问题的新视角。

一、确定“蜘蛛”的位置

例1如图1，小明手中有一张矩形纸片ABCD，AB=4，AD=9。点K在这张矩形纸片的边AD上，DK=3，将纸片折叠，使AB落在CK所在直线上，折痕为HI，点A、B分别落在点A′、B′处，小明认为B′、I、D三点共线，他的判断是否正确，请说明理由。

图1

【思路分析】这三只“蜘蛛”B′、I、D共线吗？我们可以选择其中两个点求出其直线表达式，然后将第三个点代入验证即可。本题中矩形的几何背景与相似关系为这样的做法提供了保障。建立如图2 所示的平面直角坐标系，过点B′作B′B″⊥BC，利用相似的有关知识可以求得，从而求得直线B′I的表达式为，再将点D（9，4）代入该直线表达式中，得，所以B′、I、D三点不共线。

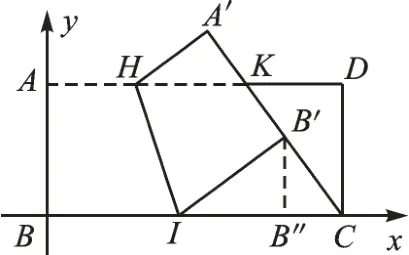
图2

【归纳总结】平面直角坐标系的“定位”功能是刻画并确定点的位置最有力的工具。以后，我们在遇到描述点的位置问题时，在条件允许的情况下就可以考虑通过建立平面直角坐标系解决问题。

二、计算“蜘蛛”间的距离

例2如图3，矩形ABCD中，AB=6，AD=6，点E在AB上，且AE=2。将该矩形沿EF折叠，使点B恰好落在AD边上的点P处，连接PB交EF于点G，连接PF、DG，它们相交于点H，求HD的长。

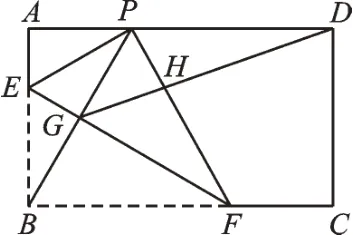
图3

【思路分析】如果要求两只“蜘蛛”之间的距离，还可以建立平面直角坐标系来求吗？当然可以。本题的几何背景依然是易于建立平面直角坐标系的矩形，且由于翻折变换，还形成了大量的相似三角形，这些相似三角形都是两个内角为30°、60°的直角三角形。我们不难发现，建立平面直角坐标系后，除了点H，其他点的坐标都可以通过相似或锐角三角形函数的知识求得。建立如图4 所示的平面直角坐标系，可以求得。因为点H可以视为直线DG与直线PF的交点，所以在求出直线PF的表达式y=-x+12和直线DG的表达式y=后，联列方程解得便可求出点H的坐标为再根据点H与点D的坐标，运用勾股定理求出HD的长。过点H作HH′⊥CD，根 据 勾 股 定 理 得

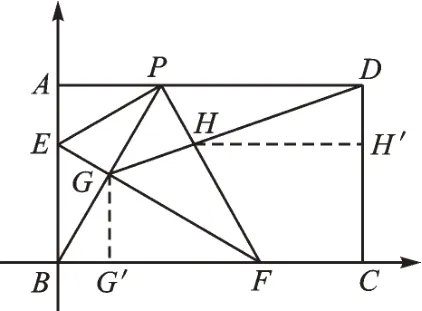
图4

【归纳总结】要求两点之间的距离，我们可以建立平面直角坐标系，通过分析题目中的几何关系，赋予每一个点精准的坐标，再利用勾股定理的相关知识便可解决问题。

三、研究“蜘蛛”的轨迹

例3如图5，Rt△ABC中，∠C=90°，AB=5，BC=4。点G为边BC的中点，点D从点C出发沿CA向点A运动，到点A停止，以GD为边作正方形DEFG，求点E的运动路径的长。

图5

【思路分析】“蜘蛛”沿着一条直线动起来了怎么办？如果点的运动轨迹是一条直线，那不就是我们熟悉的一次函数吗？只要我们设出这个动点的坐标并找到该动点坐标背后的函数表达式，那么就可以准确地找到这只“蜘蛛”的运动轨迹。建立如图6 所示的平面直角坐标系，过点E作EE′⊥y轴，垂足为E′，设DC=t，根据全等的相关知识可得点E的坐标为（-t，t+2），所以点E在直线y=-x+2 上运动。“蜘蛛”运动路径的长如何求呢？在找到该动点所在的函数表达式后，根据条件中提供的运动范围找到该动点的起终点，由题意可知0≤t≤3。当t=0 时，y=2，此时点E的坐标为（0，2）；当t=3时，y=5，此时点E的坐标为（-3，5）。再根据勾股定理求得点E运动的路径长是

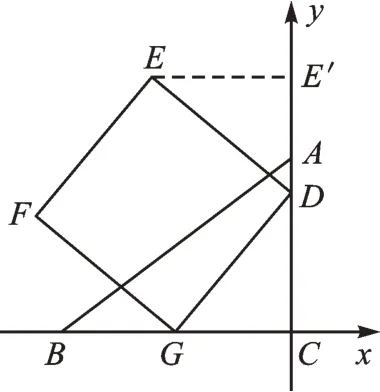
图6

【归纳总结】研究动点的轨迹是较为灵活的探究性问题，建立平面直角坐标系后利用函数的相关知识可以量化动点的运动过程，这是一种更便捷的“代数”策略。