SiCp/Al陶瓷复合材料制动块磨损数值模拟
2022-06-21杜丹丰王麒麟
杜丹丰 王麒麟
(东北林业大学交通学院,黑龙江 哈尔滨 150040)
车辆制动性能的稳定性是决定汽车行驶安全的关键因素,车辆制动时产生的“热衰退”效应会导致车辆出现制动失效的问题。同时,制动块的过度磨损也会影响车辆的制动效能。盘式制动器具有稳定性强、结构简单等优点,其已经在乘用车领域占据主导性地位[1]。SiCp/Al复合材料具有密度低、热膨胀系数小、耐高温、耐疲劳以及耐磨损的特点,其凭借良好的耐磨损性能被广泛应用于航空航天、交通运输等领域[2-5]。为了研究SiCp/Al材料作为汽车制动块的实用性,该文建立了三维盘式制动器热力耦合有限元模型,并通过UMESHMOTION子程序计算单次制动过程中制动块的磨损深度,分析采用SiCp/Al制动块对制动过程中盘式制动器热弹性耦合特性的影响。
1 建立热弹性耦合过程的数学模型
1.1 制动过程摩擦热的产生及分配
假设汽车制动消耗的动能全部转化为摩擦副产生的热量,制动盘与制动块之间相互摩擦表面的热流密度q0满足公式(1)[6]。

式中:z为制动器的制动效能,其数值是车辆的减速度a和重力加速度g的比值;φ为制动器制动力分配系数;Ad为摩擦副实际接触面积,m2;b为车辆制动初速度,m/s;εp为制动盘表面载荷的分布系数;m为整车质量,kg。
1.2 建立盘式制动器热弹性耦合模型
为了研究制动过程中制动器温度的变化规律,该文采用瞬态热分析方法,并基于傅里叶方程及能量守恒定律开展相关研究工作。在笛卡尔坐标系下,瞬态热分析中温度场的控制方程如公式(2)所示[7]。
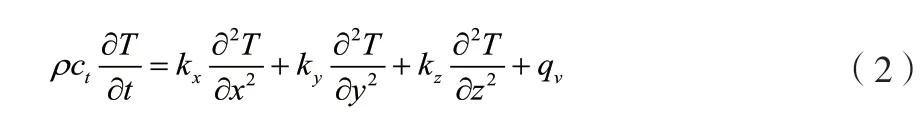
式中:T为物体温度分布状态,℃;ρ为材料密度,kg/m3;ct为某一温度下材料的比热,J/(kg·K);kx、ky以及kz为材料沿着坐标轴方向的热传导系数(该研究认为材料为各向同性材料);qv为内热源强度,W/kg(其来自摩擦副产生的摩擦热);t为当物质比热容随温度变化时给定的温度,℃;x、y以及z为坐标轴方向。
根据圣维南原理将六面体单元的正应变简化为热应变及机械载荷产生应变的叠加。根据线弹性本构关系六面体单元的正应变方程如公式(3)所示[7]。
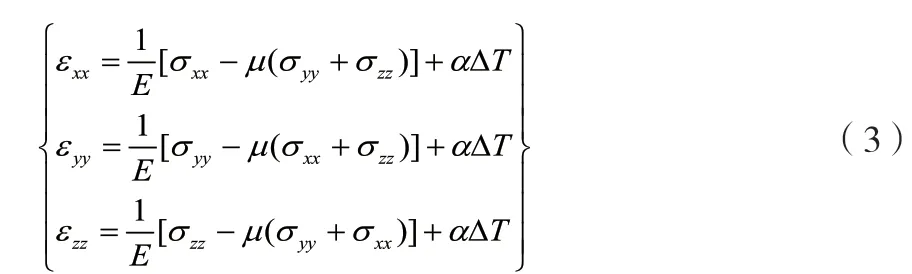
式中:εxx、εyy以及εzz为六面体单元沿坐标轴方向的正应变;E为材料弹性模量;σxx、σyy以及σzz为六面体单元沿坐标轴方向的应力;μ为材料泊松比;α为材料热膨胀系数。
1.3 建立制动块磨损模型
制动块摩擦过程的磨损深度由摩擦对偶件材料属性、接触压力以及滑移速度等因素决定,结合对试验结果的分析产生了多种磨损量数值的模拟方法,该文选用应用较为广泛的Archard公式[8],其磨损模型如公式(4)所示。

式中:V为磨损体积,mm3;s为磨损位移,mm;k为无量纲的磨损系数;FN为法向载荷,N;H为摩擦表面的硬度,N/mm2。
用磨损深度方程将时间微元Δt及接触面积ΔA离散化为微分形式,如公式(5)所示。

式中:Δh为磨损深度,mm;kd为比磨损系数(k/H);Δs为时间增量内的滑移增量,mm。
根据车辆行驶工况建立制动衬片磨损深度数值模拟模型如图1所示。
2 建立热弹性耦合过程的有限元模型
2.1 建立盘式制动器的三维模型
利用3D软件Solidworks建立通风盘式制动器的几何模型。制动器模型几何尺寸见表1。为了方便网格划分,对模型的部分元件进行简化,简化后的模型如图2所示。
2.2 确定摩擦副材料参数
制动盘的材料参数选用HT250灰口铸铁的各项热物理参数,制动盘及金属基制动块的具体参数见表2、表3,SiCp/Al复合材料的性能参数见表4[9]。

表1 盘式制动器模型几何尺寸

图1 制动块磨损深度数值模型

图2 通风盘式制动器的三维模型
2.3 确定制动工况
假设汽车以120 km/h的初速度行驶,再以10 m/s2的减速度紧急制动至车辆停止,车轮半径为0.28 m,则车辆的初始角速度为1137.39 rad/min,制动时间为3.34 s。
2.4 确定网格划分及边界条件
制动盘几何结构相对规则,对制动盘进行六面体结构化网格划分,制动盘和制动块均采用缩减积分温度-位移耦合单元C3D8RT,划分得到制动块网格节点数为3 641,单元数为2 838,制动盘整体被划分为21 478个节点、13 856个单元。制动块与制动盘节点划分结果如图3、图4所示。

图3 制动块网格节点划分图
采用主从面对应法定义制动盘与摩擦面之间的接触,将划分网格较大的制动盘表面定义为主面(有利于计算结果收敛)。将5组不同温度下的摩擦系数(见表5)导入有限元模型中[10]。
热弹性耦合过程求解过程分析步选择温度-位移耦合分析步。在制动块两侧施加4 MPa的恒定压力载荷,只保留制动块上表面的压力方向自由度。在制动盘内圈节点施加转速,转速随时间下降至0 r/min。设置环境温度为20 ℃,同时也将模型初始温度定义为20 ℃。
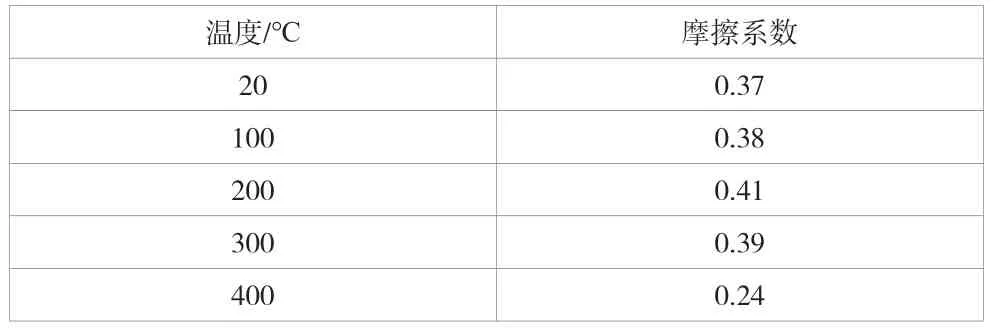
表5 不同温度下的摩擦系数
2.5 建立及关联磨损子模型
在每个增量步结束后,ALE程序将从结果文件中读取每个节点的滑移速率、接触压力。
通过UMESHMOTION子程序调用数据计算节点移动速度及方向,建立磨损数值模拟模型,建立的磨损数值模拟模型如下。

图4 制动盘网格节点划分图

3 仿真结果及分析
3.1 建立分析结果采样点
为了研究制动盘和制动块温度、应力变化的特点以及制动块的磨损速度,沿制动盘径向选择4个节点a、b、c和d,沿制动块周向选择3个节点e、f和g,如图5所示。
3.2 紧急制动过程盘式制动器温度场的分布
紧急制动结束,制动过程产生的热量在向其他位置传导的同时,还会与外界环境进行热交换。当盘式制动器紧急制动3.34 s结束时,温度分布如图6所示。传统制动盘最高节点温度达到218.85 ℃,制动盘高温区域以“热点”形式周向分布,并且向两侧扩散,温度最大值出现在接触区域入口处。而SiCp/Al材料导热能力强,制动产生的热量大量向外部环境扩散,导致高温区域存在于摩擦接触部位局部,整体温度明显低于传统制动盘。
在紧急制动工况中,盘式制动器温度整体呈现先快速上升达到峰值后平稳下降的特点,制动盘采样点温度变化规律如图7所示。在制动初始0.2 s内,2种制动器制动盘温度均快速上升,随着制动过程中转速逐渐降低,升温速率也不断下降,当产生的热量与散热量相等时,温度达到峰值。传统制动盘温度峰值达246.76 ℃,而与SiCp/Al材料制动块对应的制动盘温度峰值为146.05 ℃,与传统制动盘相比,其温度峰值下降40.64%。这是由制动块陶瓷材料良好的导热性能及其自身强耐热性共同作用的结果。
3.3 紧急制动过程盘式制动器应力场分布

图5 盘式制动器采样点分布图
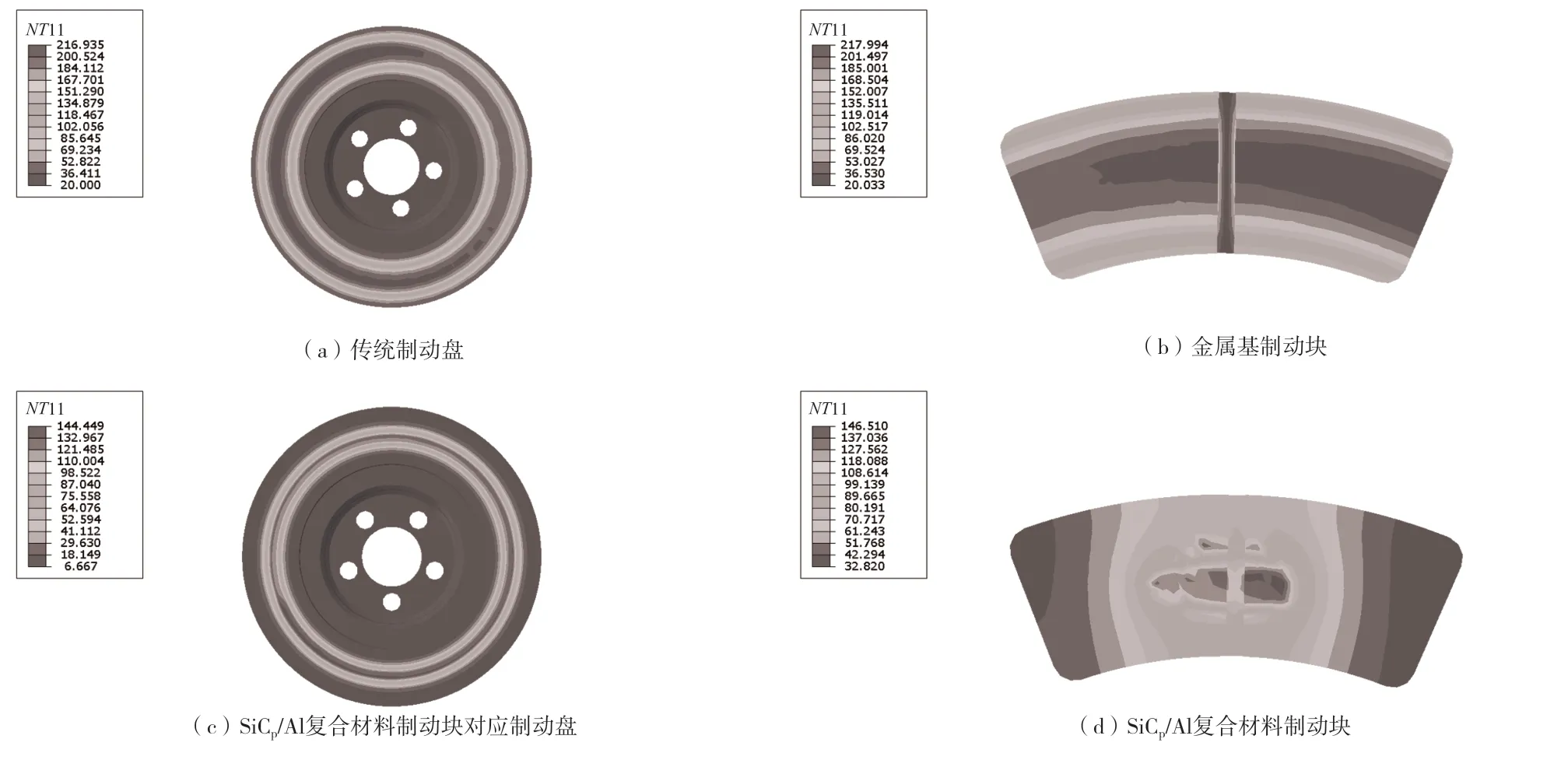
图6 紧急制动3.34 s时盘式制动器温度分布云图

图7 制动盘采样点温度变化曲线

图8 紧急制动3.34 s时盘式制动器应力分布云图
在经历一次紧急制动过程后,盘式制动器的应力分布如图8所示。对制动盘来说,与轮轴连接侧的应力要远高于另一侧,传统制动器制动盘应力最高点达到260.52 MPa,应力集中且具有明显的“斑点”状,沿周向分布在摩擦接触区域中。对制动块来说,摩擦接触表面的应力明显低于浮动钳一侧,最大应力保持在6.97 MPa,配置SiCp/Al制动块的制动器的制动盘及制动块应力明显降低,制动块应力分布趋向于由中央向外侧均匀扩散,制动盘应力分布也更加均匀。
3.4 紧急制动过程制动块磨损分布特点
在制动过程中,制动块受温度及应力变化影响产生的主要变化体现为受压方向的变形。其变形量是制动压力、内部热应力、热膨胀以及表面磨损共同作用的结果,这也是影响制动块使用寿命的关键因素,传统制动块及SiCp/Al材料制动块Y轴方向变形量如图9所示,传统制动块摩擦接触边缘变形最严重,在一次紧急制动过程中可以达到446.13 μm,而SiCp/Al制动块变形明显更加均匀,中心部位几乎不产生变形,制动性能更加稳定。
利用子程序导出制动块采样点的磨损量,得到的制动块采样点磨损深度如图10所示。金属基制动块在摩擦接触边缘磨损严重,经历单次紧急制动过程后,边缘磨损深度可达257.68 μm。而SiC/Al材料制动块边缘磨损深度最高只有13.74 μm,磨损深度只有金属基制动块的5.33%,由于其制动过程中接触应力小,且材料本身具有更强的耐磨性,因此磨损程度远低于传统制动块,使用寿命更长。
4 结语
该文通过建立通风型盘式制动器热弹性耦合模型分析了采用SiCp/Al复合材料制动块对盘式制动器的温度场、应力场、变形量及磨损深度的影响,得出的结论如下:1) 在紧急制动过程中,与传统金属基制动块相比,应用SiCp/Al复合材料制动块可以使制动盘温度峰值下降40.64%,从而有效地缓解制动性能出现“热衰退”现象,进而提高车辆制动的稳定性。2) 与传统制动块相比,SiCp/Al材料制动块节点应力最大值下降约2.02 MPa,在制动过程中米塞斯应力更小,更不易发生断裂,轴向变形量更小,制动性能更加稳定。3) 在紧急制动过程中,制动块先快速磨损,集中于摩擦接触入口部位,接触应力平稳后,磨损量趋于平稳增长,金属基制动块单次制动磨损深度最高可达257.68 μm,SiCp/Al复合材料制动块单次磨损深度峰值为13.74 μm,只有传统金属基制动块磨损深度的5.33%,具有更强的耐用性。
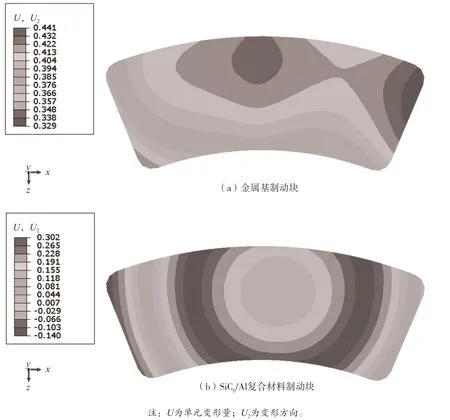
图9 紧急制动制动块Y轴方向变形量

图10 制动块采样点磨损深度曲线
[9]朱戈,黄树涛,许立福,等.SiCp/Al复合材料制动盘的温度场仿真分析[J].兵器材料科学与工程,2019,42(6):44-50.
[10]冯世波,罗艳蕾.基于ABAQUS的刹车盘热应力分析[J].现代机械, 2013(5):28-30.
