立足核心素养，打通小学数学知识的“隔断墙”

詹海洲

【摘要】新时代小学数学教育强调立足核心素养，关注从教学大纲到课程标准的变化，让学生在参与教学活动中逐步形成和发展必备品格、关键能力，这个变化带来了以知识为本到以人为本的教育理念的变化。

【关键字】小学数学;核心素养;还原本质;认知冲突;隔断墙

未来社会应用的情境千变万化，我们现阶段所学的一种知识或是一种方法可以适应于未来多元的情境吗？所以立足核心素养，帮助孩子形成知识或是方法的脉络，让孩子打通体系间的“隔断墙”是数学教育的重要思想。

一、打通“隔断墙” ——解决认识冲突的需要

“认知冲突”既能激起学生的思维振荡，又会催生乐于探究的积极性。小学数学核心素养中也提到应充分利用教材中出现的矛盾因素以及来设置问题。让“冲突”打通“隔断”。既然冲突这么重要，那如果冲突不够强烈，对孩子的认知就不够深刻。比如三年级中的乘法教学，我们创设“坐火车”的情境，每节车厢均坐6人，从相同加数引入四节车厢的人数6+6+6+6，但是加数个数如果比较少，孩子体会不到乘法简便性的特点，如果车厢再多一节呢？相同加数的个数就变成6+6+6+6+6，认知冲突就强烈点，但还有个别孩子喜欢用加法，也不用乘法。所以我们要让冲突来得更猛烈些，如果是100节车厢呢？这样更巧妙地打通了加法和乘法的“隔断墙”，让孩子淋漓尽致地体会到乘法的优势。

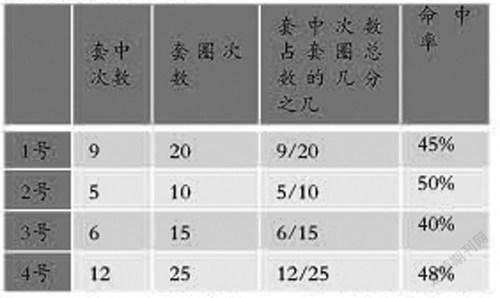
另外，对于百分数教学很多人知道百分数是一种特殊的分数，看重它作为数的教学，数的读写、百分数和一般分数的不同、是不是大于1、为什么不能加单位等，却忽略了它作为数据统计量的意义。我们通过投篮或是套圈创设活动，先比较1号和2号同学的命中率：9÷20=9/20，5÷10=5/10，此时分母存在整数倍关系，孩子还是习惯于旧知，无法打通分数和百分数间的隔断墙。我们加大冲突，让孩子比较3号和4号之间的命中率：6÷15=6/15 ，12÷25=12/25，此时的通分难度加大。再加大冲突让孩子比较1 号、2号、3号、4号之间的命中率，引出更强烈的冲突，打通了通分和难以通分，倍数和不是倍数关系，分数、小数之间的“隔断墙”，体会统一比较标准的重要性，感受到以百分数为标准进行比较的合理性。

二、打通“隔断墙” ——知识“网格化”的需要

知識“网格化”是学生形成体系思维的必要条件，是综合多种能力解决问题的基础。比如对于整数、小数、分数、百分数中解决问题的教学， 我们设计如下：（1） 小车的速度是80千米/小时，比自行车速度的4倍多20千米，，请问自行车速度多少？（2）李明六月份跑步22;5;8千米，比五月份的1;5倍少0;5千米。李明五月份跑了多少千米？（3）果林里有苹果树360棵，比杏树的3/5多60棵，杏树几棵呢？（4）源福商场2022年五月份营销总额1600万元，比2021年五月份营销总额的110%还多50万元。你能求源福商场2021年五月份的营销额吗？以上四题分别是整数、小数、分数、百分数解决问题的典型代表，在日常教学中，很多老师立足于年段孤立地进行教学，没有帮孩子理清其中的线性联系，更难形成“网格状”的思维体系。如果我们立足网状视角，就会洞察其中的联系。生成一个模型：A比B的几倍（几点几倍、几分之几、百分之几）多多少，已知A，求B;理清关系，根据关系构建线性思维。并且立足整数的数量延伸到分数、百分数的数量关系，立足知识的“前世”打通知识的“后身”，形成网格思维。

网格化就是纵横联系，数学核心素养中强调我们要立足于知识的横向联系和纵向联系，形成知识的网状联系，形成多线性思维。

比如：你知道它们的联系吗？  97÷4     9;7÷4     1/2 ÷ 3

我们将整数除法和小数除法竖式计算后发现97÷4 =24，24由2个10、4个1组成;9;7÷4=24;25，24;25由2个10、4个1、2个0;1、5个0;01组成。竟然发现和计数单位有关系。那对于分数除法1/2 ÷ 3呢？是不是如此，我们尝试在猜想中展开计算：1/2 ÷ 3=1/2×1/3=1/6，那1/6是不计数单位呢？

我们又结合图示帮助孩子理解。通过这样系列的思维模式打通整数除法、小数除法、分数除法之间的“隔断墙”，原来计数单位对于“×”“+”是累加的作用，对于“÷”“-”是细分的作用。以计数单位为统领，又将“+-×÷”之间的“隔断墙”打通了。我们更好地理解了十进制、位值、计数单位代表的小数意义，小数意义又为小数除法运算提供了基础。

三、打通“隔断墙” ——发展多学科思维的需要

核心素养中对于“隔断墙”的定义其实有两个层次，一个学科内部的线性联系，一个是多学科思维的多线性联系。我们要做“心上有人，眼中有线”的人。比如五年级“测量不规则物体的体积”，首先打通小“隔断墙”，未放测量物前，先量出一定的水V前;再把待测物浸没水中然后测出体积V后;后把两者相减的差即V = V后 – V前为待测物体积V。整合了了水测法之后，孩子只是初步感知工具的重要性，怎样让思维的认知更深呢？我们又引出新的问题，如果没有量杯，只有长方体或正方体容器，还能用排水法测量不规则物体的体积吗？这时就要“从读到算”“从看到量”进行升华了，打通科学和数学的隔断——排水法。很多人讲到这一步就停止，那样学科的联系不紧密，孩子的思维深度和创造性是不够的，所以又引入新的问题“如何测量形状不规则而比水轻的物体的体积呢”，数学又和浮力知识联系起来，从而引入用量筒（挂重法）或用量筒（针压法），孩子在以数学为基础上，整合多种知识步步深化，贯穿学科的多线性思维就产生了。这是我们可以引发孩子的“头脑风景”，是不是这样我们就可以测量所有不规则物体的体积了，反正世间万物不是沉于水，就是浮于水啊，从而引发孩子深度思考“可是用水可以测量不规则的物体，如果要测冰糖的体积，怎样测量”，数学又整合了融解度的问题，再次引发孩子的思索。

生1：我可以用锡纸包起来啊？

生2：那不是加大误差。

生3：而且锡纸有空气空隙，遇水又会松涨起来，误差更大了。

生4：那用胶纸包紧一点啊？

生5：啊，那就不是原来物体的体了……又抛出新的问题，步步引导孩子思考“可以用细沙或面粉等代替水”进行测量的方法，在步步深化中生成多学科的思维。

立足核心素养，打通“隔断墙”，促进深度学习，让“广度”体现“深度”。让儿童在还原思维过程中进行线性学习，更好地感受数学的魅力、数学的价值、数学的力量。

【参考文献】

[1]杨建波.数学课程标准[S].北京：北京师范大学出版社，2011（5）.

[2]李民.小学数学知识的本质是什么[S].北京：吉林大学出版社，2013（6）

[3]闫天灵.小学数学高效课堂概念教学策略的研究[D].天津：天津师范大学，2010（9）.91659CD9-C182-47A9-AAB1-FE4402AEDD96