利用转移熵研究引起磁暴扰动的太阳风参数重要性排序*
2022-06-20于佳斌佟继周方少峰胡晓彦
于佳斌 佟继周 方少峰 胡晓彦
1(中国科学院国家空间科学中心 北京 100190)
2(中国科学院大学 北京 100049)
0 引言
太阳风–磁层相互作用形成了一个多尺度耦合的复杂系统,太阳风是引起地磁暴的最主要驱动源,例如当行星际磁场南向时,行星际磁场可与地球磁场发生磁场重联,较易引发磁暴。因而,理解太阳风变化对地磁场的影响机制,是预报地磁暴的关键之一。
有关太阳风与地磁扰动之间的相关性研究,新方法不断出现,这些方法主要基于太阳风和地磁参数的解析关系、相关系数或预报模型,线性回归、统计相关等方法,已被证实是认识磁暴时地磁变化的有效方法,例如Liu 等[1]研究了太阳活动上升年的地磁Kp指数与行星际磁场南向分量Bz、太阳风速度vsw、太阳风温度Tsw与太阳风数密度Dsw的相关性,相关系数分别为0.66、0.03、0.58 和–0.45,发现有一类磁暴与Bz地磁场重联无关。Cane 等[2]统计结果表明行星际磁场南向分量Bz与 磁暴扰动指数最小值Dstmin的相关系数为0.74;Wu[3]统计分析了1995-1998 年Wind 数据,证实vswBzmin与Dstmin的相关系数为0.87,略高于行星际磁场南向分量最小值Bzmin与磁暴扰动指数最小值Dstmin的相关系数0.81。Zhang 等[4]发现行星际电场E与Dst指数有很好的相关性,并且在中、强等地磁活动期间,存在显著的突变特征曲线,相对于vsw,,vswB2和 能量耦合函数ε=,行星际电场E的突变特征曲线更易识别。Zhao 等[5]的研究表明在诸多参数中,就单一因素来说,行星际电场E对磁暴强度影响最大,行星际磁场南向分量Bz对磁暴强度影响次之;Khabarova等[6]和Ahmed 等[7]也得到了相似的结果。除此之外,Iyemori 等[8]首次成功地应用线性预测滤波方法,基于太阳风参数预测了地磁活动,Ji 等[9]和Rastätter等[10]用经验和物理模型、Ahmed 等[7]用神经网络对磁暴进行预报研究。然而,地磁系统对太阳风变化的响应是非线性的,线性统计不足以表达其完备的相关性,同时在使用各种预报模型时,不同的输入参数对磁暴的影响和重要性仍不明确,关于哪个太阳风参数对磁暴的发生更重要,还未有统一的认识。
近年来,基于信息论的新方法[11]被提出并成功地应用于揭示地球磁层–电离层系统响应太阳风变化的复杂动力学特征。Michelis 等[12]以地磁活动指数AL和Sym-H分别定量化亚暴和磁暴过程,进行了双变量转移熵分析,结果表明亚暴和磁暴之间的信息流动方向取决于全球地磁活动水平。Wing 等[13]利用信息论进行太阳风–地球辐射带系统研究,利用互信息、条件互信息和转移熵对能量范围为1.8~3.5 MeV的地球同步轨道高能电子通量的太阳风驱动因素进行了研究,得出了基于信息论分析的重要性排序。转移熵可以提供强大的无模型统计量,在太阳风–地球辐射带系统研究已经得到了验证,但目前还未在太阳风–磁层整体耦合系统中得到应用。本文利用转移熵研究太阳风参数与地磁指数之间的非线性关系,应用转移熵来衡量磁暴时的太阳风驱动因素并进行量化,对不同太阳风参数的重要性进行研究。
1 数据与方法
1.1 数据来源
用于研究的太阳风及地磁活动指数的数据均来源于美国国家航空航天局(NASA)的OMNI*http://omniweb.gsfc.nasa.gov/公开数据,具体包括分钟分辨率数据(HRO)和小时分辨率数据(LRO),时间跨度从1996 年到2018 年。OMNI 整合了来自ACE、WIND、IMP8 等航天器的太阳风磁场和等离子体数据集,并根据实际的太阳风速度时移到地球的弓激波鼻尖处。此外,本研究还使用了世界地磁数据中心(WDC)提供的地磁Sym-H指数数据、比利时SILSO 中心提供的太阳黑子数据、和加拿大自然资源部的太阳10.7 cm 射电流量F10.7数据。
本研究利用美国空间天气研究中心(SWRC)提供的空间天气数据库(DONKI)**https://kauai.ccmc.gsfc.nasa.gov/DONKI/中提取的磁暴事件列表,共计93 个事例,主要分布在第24 太阳活动周期间的2010 年到2018 年。
1.2 相关系数与转移熵
1.2.1 相关系数算法
相关系数又称皮尔逊积矩相关系数,适用于度量两个变量x与y之间的线性相关性,其值介于1 与–1之间,即
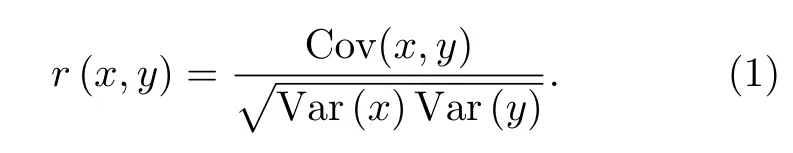
直接推导可知
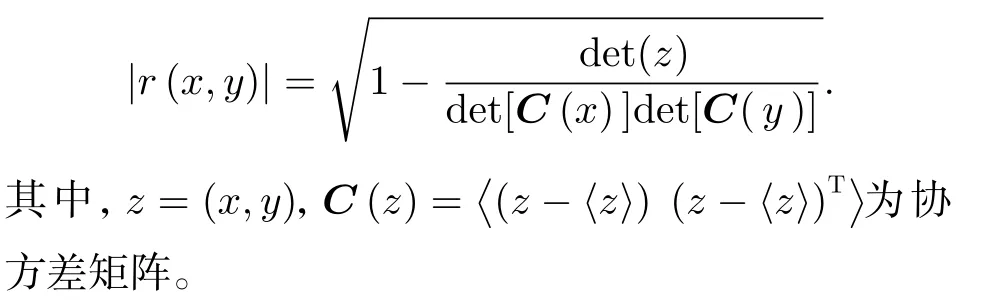
时移相关系数[13]是皮尔逊积矩相关系数度量向两个时间序列x(t)和y(t+τ)的拓展,即
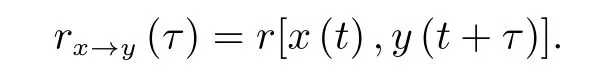
其中τ为时间延迟。当相关函数有多个峰或没有明显的不对称时,这种分析的结果可能不是特别清楚。此外,相关系数是两个变量之间线性关系的一个度量,不能用于描述非线性关系。
1.2.2 转移熵算法
度量两个变量x和y之间依赖关系,更通用的方法是通过考虑
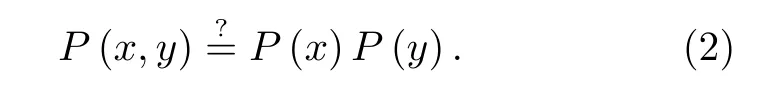
其中,P(x,y)为x和y的联合概率。如果式(2)等号成立,则表示变量x与y相互独立;相比式(1),除线性关系外,式(2)可以表达更多的非线性关系。
信息论中互信息[14]表示一个随机变量中包含的关于另一个随机变量的信息量,代表两个随机变量的依赖程度。
对于离散的概率分布,互信息的定义如下:
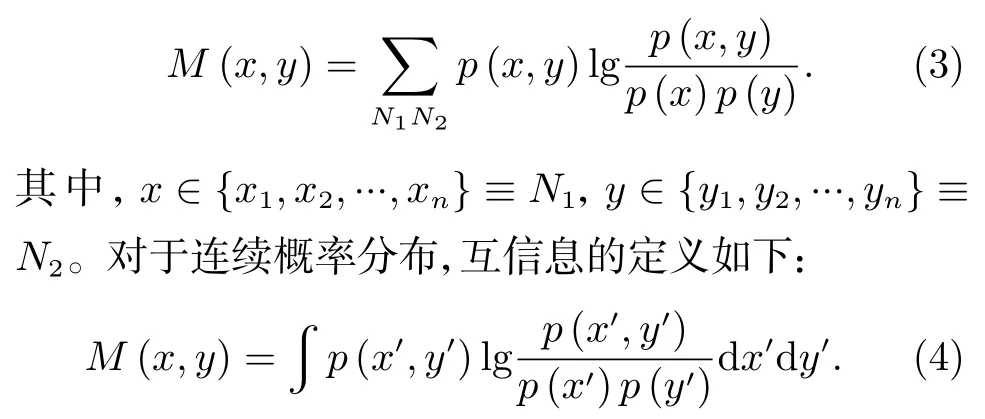
从式(3)和(4)可以看出,互信息M(x,y)对式(2)进行了定量描述,相比于相关系数,更好地表达了两个变量x与y之间的依赖关系。进一步,如果x与y服从联合高斯概率分布,互信息具有如下表达式[14]:

互信息的取值范围为[ 0,∞),经过转化Λ(x,y)的取值范围位于 [ 0,1]。特别地,当Λ(x,y)=0 时,互信息M(x,y)=0,从其定义可知p(x,y)=p(x)p(y),即x与y相互独立。
Λ(x,y)是一个同时包含线性和非线性关系的度量,而互相关系数r(x,y)和Λ(x,y)之间的差异
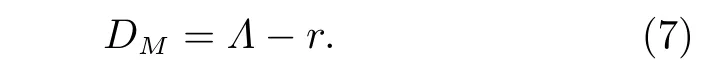
可用于揭示变量之间除线性关系之外更复杂的关联关系。
当已知z∈{z1,z2,...,zn}≡N3时,衡量x与y的互信息即条件互信息[13]有

转移熵是一个量化两个系统相关程度或混沌程度的参数,可用于处理有限长度的信号数据。转移熵定义由Schreiber[15]于2000 年提出,同时考虑源序列和目标序列的数据长度,通用的转移熵定义为(默认单位为nats)
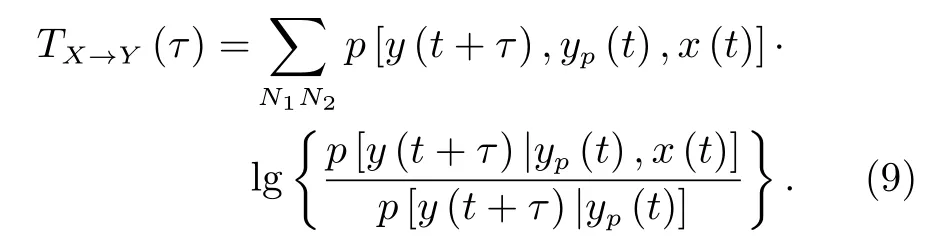
其 中,yp(t)=[y(t),y(t −∆),...,y(t −k∆)],k+1为历史时间序列的长度,∆为最小的取样间隔,τ为时间延迟。转移熵可以被视为一种特殊形式的条件互信息[13],即
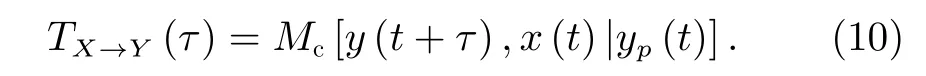
转移熵可以衡量系统中已知目标历史序列yp的情况下,有多少信息从输入序列X传递到目标序列Y的下一状态。转移熵与相关系数的不同在于方向性,即TX→Y TY →X。
转移熵算法容易受到有限大小样本效应的影响,也容易受到数值效应的影响,因此建立一个阈值来界定转移熵计算结果是否显著是必要的。为了检验计算结果的统计学意义,将源序列x随机打乱重新抽样,这一步骤保证了置换时间序列具有与原始序列相同的均值、方差、自相关函数,但破坏了非线性关系。这个过程的目的是消除两个序列数据x与y之间的所有潜在关联关系,因此计算得到的Tsur(X)→Y理论值为零。但是在有限时间序列中,由于有限样本效应Tsur(X)→Y很少为零,故而可以得到转移熵TX→Y高于Tsur(X)→Y即可认为是显著的。通过100 次随机的零假设抽样计算Tsur(X)→Y,若根据置换序列计算出的新Tsur(X)→Y值的95%小于原来TX→Y,则可以认为原始序列计算得来的TX→Y显著。
1.2.3 算法比较
运用时移相关系数、转移熵分析行星际磁场南向分量Bz与地磁指数Sym-H之间的相关性。使用1996-2018 年小时精度数据对时移相关系数和转移熵进行逐年计算。针对每一年的数据,将时移相关系数rx→y(τ)=r[x(t),y(t+τ)]的最大时间延迟设置为120 h,以步长1 h 逐步计算,即每年共120 个数据点,然后取相关系数绝对值最大的数据点作为衡量该年Bz和地磁指数Sym-H之间的相关系数计算结果,有
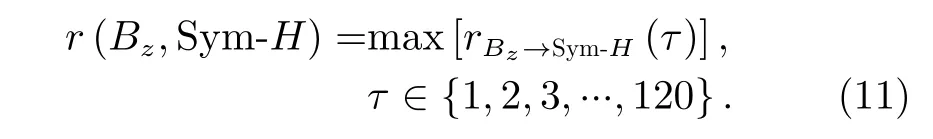
同理,计算转移熵时采用同样的时间延迟设置和最大值选取方法,由此可得图1。图1 中1996 年行星际磁场南向分量与地磁指数的最大时移相关系数r(Bz,Sym-H)=0.39;在太阳活动高年2000 年r(Bz,Sym-H)=0.35,同极小年的差异率为11%。另外,1996 年和2000 年行星际磁场南向分量与地磁Sym-H指数之间的转移熵T(Bz →Sym-H)分别为0.18 nats、0.26 nats,差异率为31%。相关系数在太阳活动高低年的差异性相对较小,转移熵在太阳活动高低年表现出明显的差异。与传统相关系数的对比表明,转移熵可以有效表征太阳风–磁层关系的相关性。
如图1 所示,转移熵的变化趋势表现出类似太阳活动周变化的双峰结构。太阳活动水平在一定程度上影响着空间天气,太阳黑子数(Nss)是描述太阳活动水平的重要指标,计算得到太阳黑子和行星际磁场南向分量与地磁Sym-H指数之间的转移熵TBz→Sym-H=T(Bz →Sym-H)的相关系数
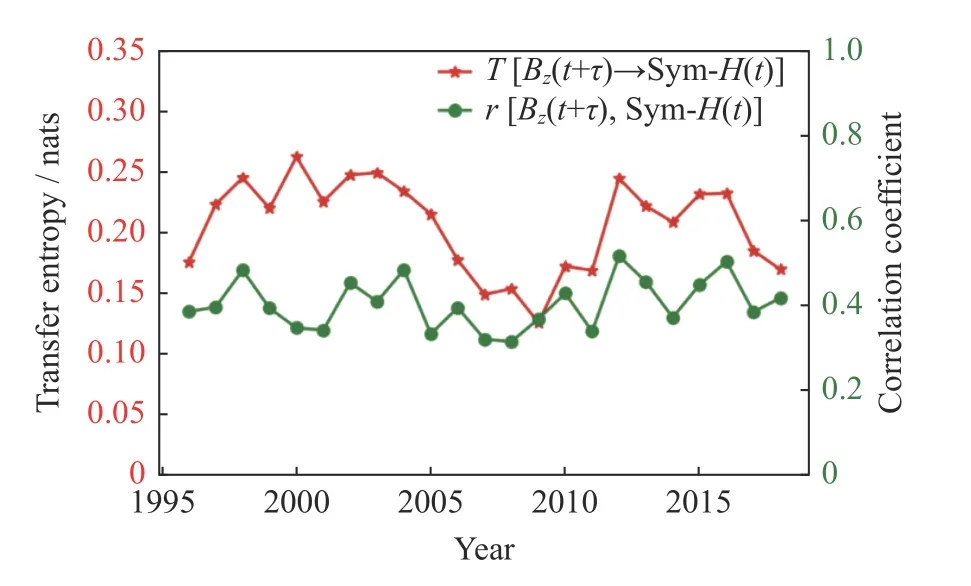
图1 行星际磁场南向分量Bz 与地磁Sym-H 指数的转移熵和相关系数Fig.1 Transfer entropy and correlation coefficient between I MF Bz and Sym-H
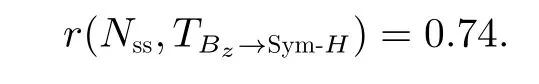
太阳黑子和行星际磁场南向分量与地磁Sym-H指数之间的转移熵TBz→Sym-H的转移熵
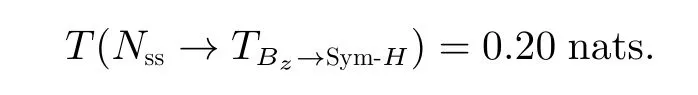
太阳黑子和行星际磁场南向分量与地磁Sym-H指数之间的相关系数rBz,Sym-H=r(Bz,Sym-H)的相关系数:

对比结果得知,
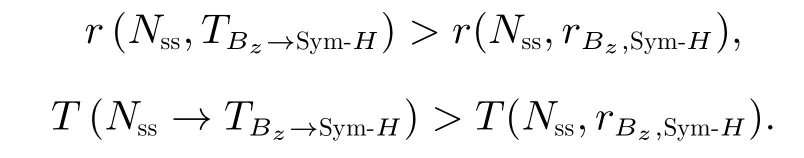
以太阳活动周期的角度看,各太阳风参数向地磁Sym-H指数信息传递的强弱与太阳活动水平的周期性变化一致。另外,太阳10.7 cm 射电流量(F10.7)是综合衡量太阳色球、过渡区和日冕极紫外辐射强度的一种常用指数,以F10.7作为衡量太阳活动水平的指标可得
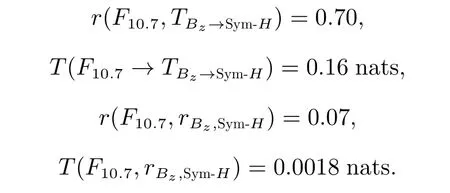
以F10.7刻画太阳活动强度,得到与太阳黑子数相同的结果。因此,转移熵可以更好地定量化太阳活动与太阳风–磁层系统的相关性。
2 太阳活动水平对太阳风–磁层相互作用的影响
以往太阳风–磁层耦合关系多参数影响因素的重要性研究,往往仅集中在个别太阳风参数,例如行星际磁场南向分量(Bz)或行星际电场(E),而与其他参数,例如行星际磁场大小(B)、太阳风速度(vsw)、太阳风数密度(Dsw)、太阳风温度(Tsw)、太阳风动压(Psw)等的综合研究较少涉及。Schwenn 等[16]发现,地磁扰动在大小和方向上都与行星际磁场波动密切相关。长期南向的行星际磁场与地球磁场之间的相互连接允许太阳风能量传输到地球磁层[17]。包括Kissinger等[18]在内的多项研究表明了太阳风速度在磁暴产生中的作用,事实上持续和增强的太阳风速度以及南向或北向的行星际磁场分量通常与行星际物质抛射有关,其被认为是磁暴的重要原因。另外,增强的太阳风密度也是一个经常影响磁暴强度的重要参数。太阳风密度的增大会导致日侧磁层顶的压缩,从而导致磁层顶流、场向流和横向流的增加。Ahmed 等[7]的研究表明太阳风密度与其他参数协同具有更好的相关性,而太阳风温度则表现较差。Xie 等[19]多篇论文描述了高速太阳风动压与磁暴的关系。Mcpherron等[20]的研究表明磁暴时的环电流积聚原则上可以直接由太阳风电场驱动。Kane[21]表示磁暴期间太阳风速度与行星际磁场南向分量vswBz的共同作用效果明显优于vsw;Wang 等[22]研究表明,对于磁暴的形成,的重要性强于行星际磁场南向分量增强的持续时间 ∆t。
标识地磁活动水平的典型地磁指数,例如Dst指数,表征了全球对称赤道环电流的强度,是四个低纬天文台的地球磁场水平分量的小时平均值[7],而Sym-H为1 min 分辨率的Dst指数。
2.1 太阳风参数与地磁指数的转移熵
实验使用1996-2018 年小时精度的太阳风数据,主要分析参数包括行星际磁场(B)、行星际磁场南向分量(Bz)、太阳风速度(vsw)、太阳风等离子体数密度(Dsw)、太阳风温度(Tsw)、太阳风动压(Psw)、行星际电场(E),以及小时精度的地磁Sym-H指数数据。
图2 展示了利用转移熵方法分析各太阳风参数与地磁Sym-H指数的相关性结果,各太阳风参数向地磁指数的转移熵的相对值表现出一定的稳定性,即:1996-2018 年中,行星际电场与地磁指数之间的信息传递TE→Sym-H均最高,随后是和,最低是和位于中部且相互差异较小,排名在各年中略有不同。各太阳风参数与地磁Sym-H指数转移熵的变化趋势表现类似于图1 中行星际磁场南向分量与地磁Sym-H指数的转移熵相似的特性:(1)在太阳活动高年,Tsw→Sym-H更为显著;(2)对于任一太阳风参数,Tsw→Sym-H在第24 太阳活动周的峰值比23 太阳活动周要低。
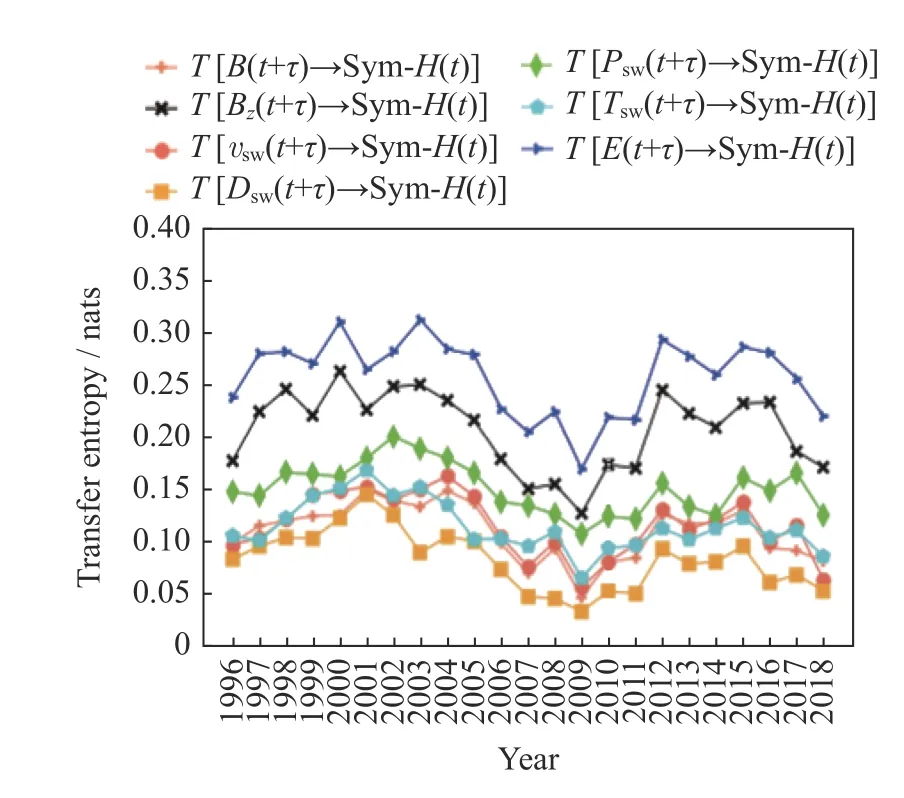
图2 各太阳风参数对地磁Sym-H 指数的转移熵Fig.2 Transfer entropy of multiple solar wind parameters to Sym-H
2.2 转移熵与太阳活动水平相关性分析
如图2 所示,除行星际磁场南向分量外,行星际磁场、太阳风速度、太阳风等离子体数密度、行星际电场及地磁Sym-H指数转移熵表现出与太阳活动周类似的双峰结构。同时将Tsw→Sym-H与太阳活动指数太阳黑子数、F10.7进行相关性分析,结果列于表1。
由 表1 可 知,r(Nss,Tsw→Sym-H)位 于[0.61,0.83]之间、r(F10.7,Tsw→Sym-H)位于[0.58,0.82]之间,均表现出较强的相关性。同时获得T(Nss,Tsw→Sym-H)位于[0.15,0.36]之间、T(F10.7,Tsw→Sym-H)位于[0.12,0.33]之间,即太阳活动指数与Tsw→Sym-H存在明显的信息传递。由此可知,以小时精度的数据分析,行星际磁场南向分量与太阳活动之间的强相关并非偶然,其他各太阳风参数与太阳活动水平也存在较强的关联,佐证了Liu 等[23]对于地球近地空间环境变化对太阳活动的依赖性。
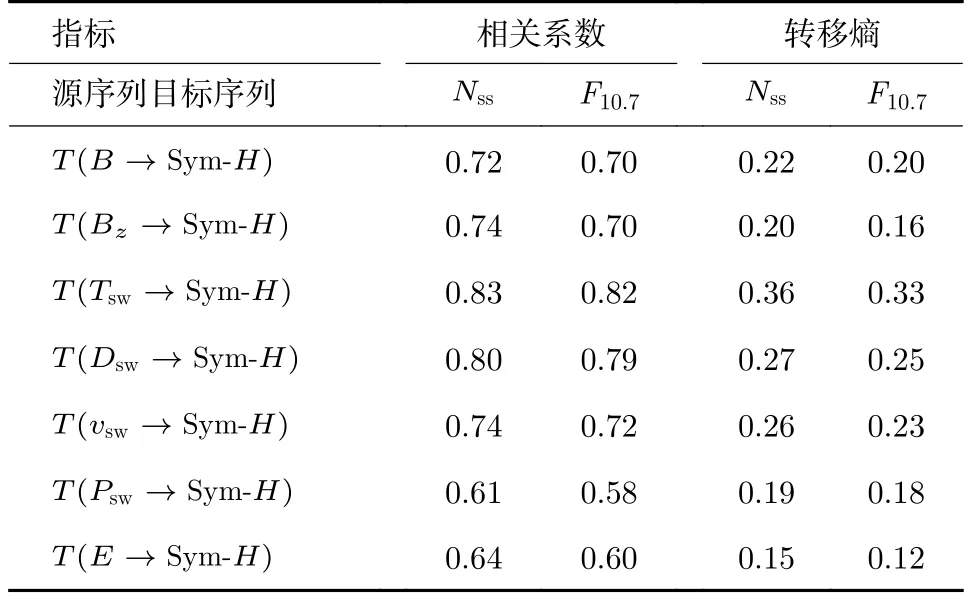
表1 T sw→Sym-H同太阳活动指数的相关性Table 1 Correlation betweenTsw→Sym-H and solar radiation
3 引起磁暴扰动的太阳风参数重要性排序
3.1 数据选择
磁暴是指整个地球磁层发生的持续十几个小时到几十个小时的一种剧烈地磁扰动,中低纬度地磁台站水平分量的显著减小为磁暴的主要特征。Wu 等[24]的研究表明,太阳扰动日变化在主相期间最强,在恢复相期间逐渐减弱。在磁暴初相和主相期间,一般会出现太阳风–磁层发电机效应,将导致磁层对流电场快速渗透到中低纬度地区;高纬焦耳加热产生全球热层扰动场,主要出现在恢复相期间[25]。磁暴主相期间,低纬水平磁场扰动(∆H)在各磁地方时(MLT)均明显下降并且出现晨昏不对称分布;磁暴恢复相期间,行星际电场(E)为负值时,∆H较主相期间弱。已有的研究表明:主相阶段主要源于环电流的增强,而影响恢复相的主要为电荷损失机制,包括电荷交换、库仑散射和波粒相互作用等[26]。因此,由于不同的物理成因,应分别研究磁暴主相和恢复相,目前本文将研究范围限定于磁暴主相阶段。
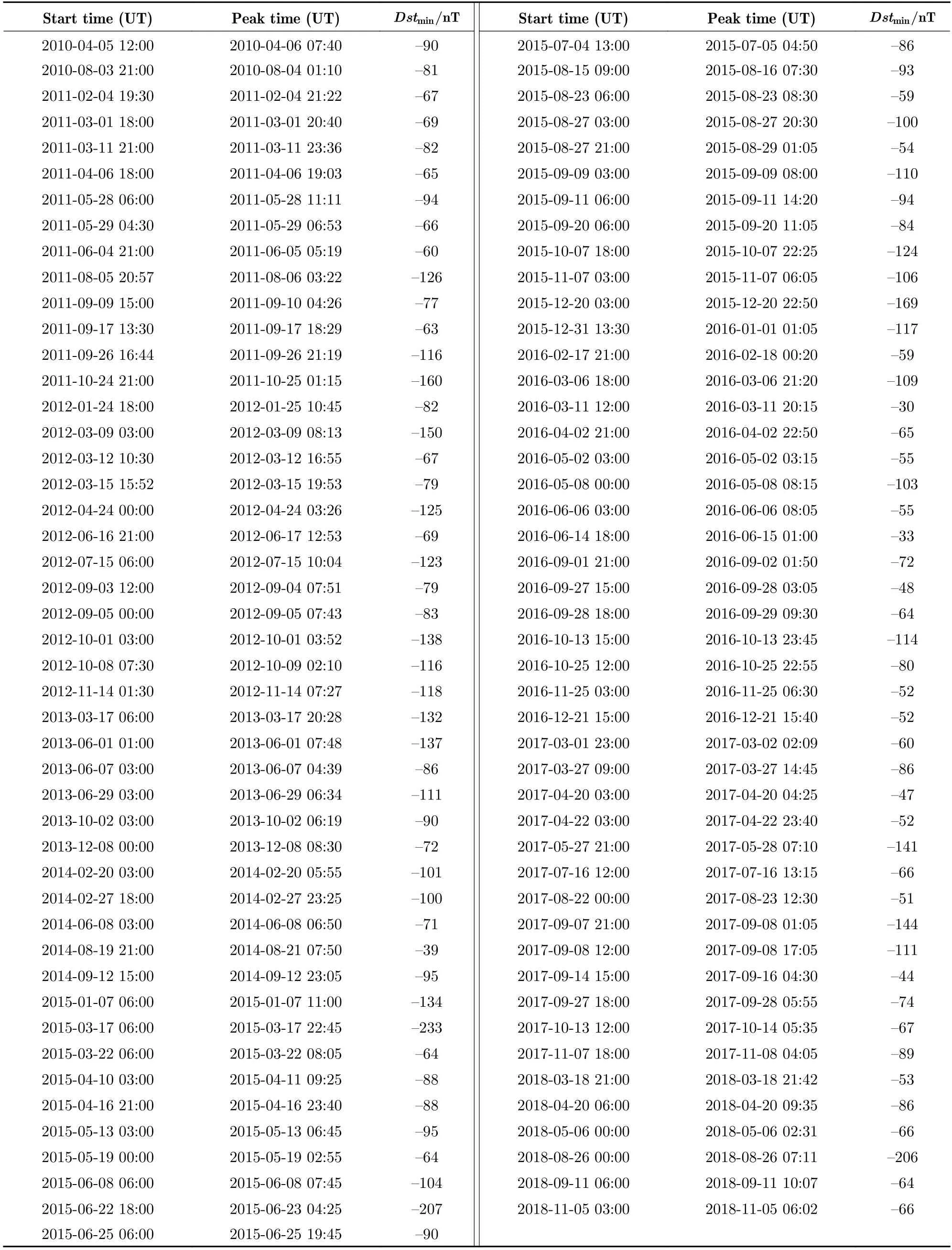
一般根据Dst峰值的不同,将地磁暴分为小磁暴(−50 nT 以往研究结果表明,地磁指数对太阳风变化的响应时间普遍小于3 h[11,28],本研究将响应时间范围设定在0 至500 min,与Stumpo 等[11]研究磁层电离层对太阳风的响应时间范围一致。以往的转移熵往往集中在单个时间序列,而磁暴期间的重要性系数为磁暴集合(见表2)上的太阳风参数对地磁Sym-H指数的转移熵平均值,故而定义 表2 2010-2018 年磁暴事件Table 2 Geomagnetic storm events from 2010 to 2018 其中〈·〉代表在表2 磁暴集合上的平均值。 相应地由转移熵定义的重要性系数为 以及定义信噪比(S/N),显著性检验指标 转移熵算法通过置换时间序列[15]来创建零假设下的概率分布来计算噪声,噪声的均值和标准偏差是由100 次随机的零假设抽样计算Tsur(X)→Sym-H平均而来。 对行星际磁场南向分量(Bz)和地磁Sym-H指数之间的转移熵进行计算,分析两者之间的信息流动。首先对每个磁暴事件进行独立的转移熵分析,而后按照式(12)以相同的时间延迟τ计算多个磁暴事件转移熵(τ)的平均值(τ)。由图3 可以看出,转移熵在τ=60 min时达到最大值Tpeak= 0.244 nats、Γ=0.196 nats,信噪比δS/N=4.15和显著性αsig=36.83σ。转移熵明显大于噪声,即信息传递显著。而基本都处于背景噪声的内部或边缘,不显示任何明显的时间延迟特征,信息传递不显著。 图3 行星际磁层南向分量 Bz和 地磁Sym-H指数的转移熵Fig.3 Transfer entropy of B z and Sym-H 经比较,上述结果与Runge 等[28]的结论基本一致,即行星际磁场南向分量(Bz)扰动是导致行星际条件变化的重要部分;Stumpo 等[11]的研究也表明,在时间延迟τ=60 min 时行星际磁场南向分量(Bz)与Sym-H指数之间有较强的信息传递。但是已有研究并未涉及太阳风温度(Tsw)、行星际电场(E)等太阳风参数的综合比较。进一步利用转移熵分析磁暴期间其他太阳风参数,包括行星际磁场(B)、太阳风速度(vsw)、太阳风等离子体数密度(Dsw)、太阳风温度(Tsw)、太阳风动压(Psw)和行星际电场(E),对Sym-H指数的影响,结果如图4 所示。 由图4 可知,各太阳风参数对地磁Sym-H指数的转移熵均高于噪声;而则处于噪声边缘,缺乏显著性。最大值出现的时间普遍小于3 h,反应出磁层对太阳风变异性的响应是突变式的激增,表现为短时间内一个强烈的信息传递。表3 根据各太阳风参数到地磁Sym-H指数的转移熵,得出了各太阳风参数的重要性系数序列。 由表3 可知,以转移熵构建的重要性系数为指标,排在第一位的是行星际电场(E),ΓE=0.200 nats。第二位是行星际磁场南向分量(Bz),ΓBz=0.196 nats,略低于ΓE。然后排名依次是太阳风速度(vsw)、太阳风温度(Tsw)、太阳风密度(Dsw)、行星际磁场(B)。最低的是太阳风动压(Psw),ΓPsw=0.135 nats。 值得注意的是图4(f),行星际电场(E)对地磁Sym-H指数的转移熵在τ=60 min时达到最大值Tpeak= 0.252 nats、Γ=0.200 nats,信噪比δS/N= 3.92 和显著性αsig=37.43σ,也有明显的信息传递,甚至比更强烈。 表3 中排在第三位的是太阳风速度(vsw),结合图4(d)可知在τ=140 min 时达到最大值Tpeak= 0.210 nats、Γ=0.159 nats,信噪比δS/N=3.15和显著性αsig=29.92σ。行星际磁场南向分量和磁层的重联是引发磁暴等空间天气事件的重要因素。Zhang 等[4]进一步得出,行星际磁场南向分量与太阳风速度的联合作用又体现于行星际电场的时变曲线,统一表现为行星际电场,太阳风速度的变化影响着磁层对流电场,从而影响环电流的形成快慢与强度。因此,从信息传递的角度分析,行星际电场扰动是磁暴发生的主要驱动因素。以往太阳风温度(Tsw)、太阳风密度(Dsw)、行星际磁场(B)、太阳风动压(Psw)等综合研究较少,从转移熵的角度出发,本文给出了这些太阳风参数在引发磁暴时的相对重要性。 图4 行星际磁场(B )、太阳风速度(vsw)、太阳风等离子体数密度(D sw )、太阳风温度(Tsw)、太阳风动压(Psw)、行星际电场(E)对地磁Sym-H 指数的转移熵Fig.4 Transfer entropy of interplanetary magnetic field (B),solar wind speed (vsw),solar wind plasma number density (D sw) ,solar wind temperature (Tsw) solar wind dynamic pressure (Psw),the interplanetary electric field (E) and Sym-H 表3 太阳风参数对地磁Sym-H 指数重要性系数排序Table 3 Importance ranking of solar wind parameters to geomagnetic index Sym-H 以相关系数为基础进行排序,由表3 中的|r|列可知,前三位仍是行星际电场(E)、行星际磁场南向分量(Bz)和太阳风速度(vsw),但是行星际磁场(B)的相对重要性提升至第四位,太阳风温度(Tsw)下降至第六位。根据1.2 节的讨论可知,相关系数仅能挖掘变量之间的线性关系,而从概率角度出发的转移熵可以挖掘变量之间更一般的非线性依赖关系,转移熵和相关系数排序的差异,表明了太阳风参数与地磁Sym-H指数之间关系的复杂性。进一步通过式(7)计算DM来对差异进行定量刻画,DM >0 揭示太阳风–磁层之间线性关系之外更复杂的关联性。由此可知,相对于相关系数,转移熵方法可以更多地挖掘参数间的非线性关系,故而导致了重要性排序的差异。 综上所述,行星际电场(E)的变化是引发地磁暴的主要驱动因素,这与Zhao 等[5]的研究结果基本一致。行星际磁场南向分量(Bz)与地磁Sym-H指数之间的重要性系数略低于ΓE,但是明显高于其他太阳风参数的Γsw。太阳风动压(Psw)与地磁Sym-H指数之间的重要性系数最低;其他各太阳风参数在引发磁暴时的相对关联程度由表3 给出。 应用转移熵研究了地磁扰动的太阳风驱动因素,可以得出如下结论。 (1)从太阳活动周期的角度分析,各太阳风参数向地磁Sym-H指数信息传递的强弱与太阳活动水平的周期性变化一致。 (2)磁暴期间各太阳风参数向地磁Sym-H指数信息传递,最相关的变量是行星际电场(E),行星际磁场南向分量(Bz)次之,然后排名依次是太阳风速度(vsw)、太阳风温度(Tsw)、太阳风等离子体数密度(Dsw)、行星际磁场(B),最弱的是太阳风动压(Psw),各参数信息传递强弱排名见表3。 (3)行星际电场与地磁指数之间的信息传递TE→Sym-H在τmax=60 min 处达到峰值,比TBz→Sym-H略高,佐证了Zhao 等[5]的研究。 在研究太阳风–磁层系统响应太阳风条件变化时,运用转移熵可以推断太阳风–磁层的非线性关系。本文将转移熵方法推广至磁暴事件集合上的平均转移熵,定义了磁暴期间太阳风参数与地磁Sym-H指数的重要性系数,并综合考虑了7 种太阳风参数,以重要性系数为依据获得了引发磁暴扰动的太阳风参数重要性排序。转移熵定量描述太阳风与磁层参数之间的非线性信息传递,为探索磁层对行星际太阳风扰动的响应过程提供一条数据驱动的研究途径,为模型研究提供参数选择的依据,由此可加速建模过程。未来转移熵在空间天气领域可以通过更多事件统计研究开展广泛应用。 致谢数据分析环境由国家科技资源共享服务平台之一的国家空间科学数据中心(http://www.nssdc.ac.cn)提供。3.2 重要性排序方法
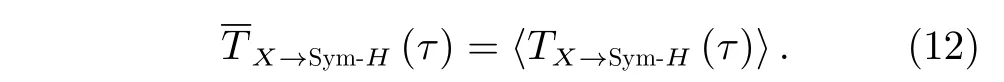
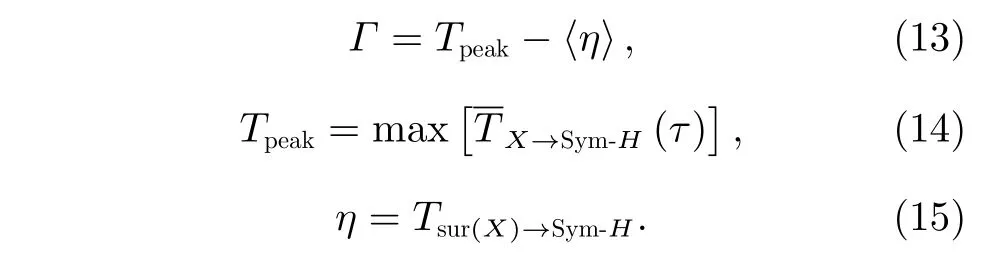
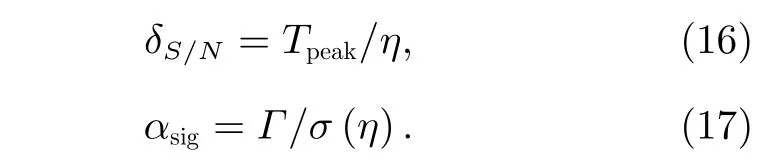
3.3 重要性排序
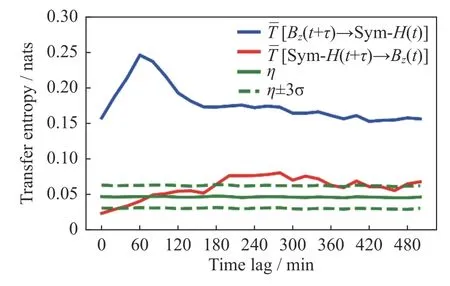
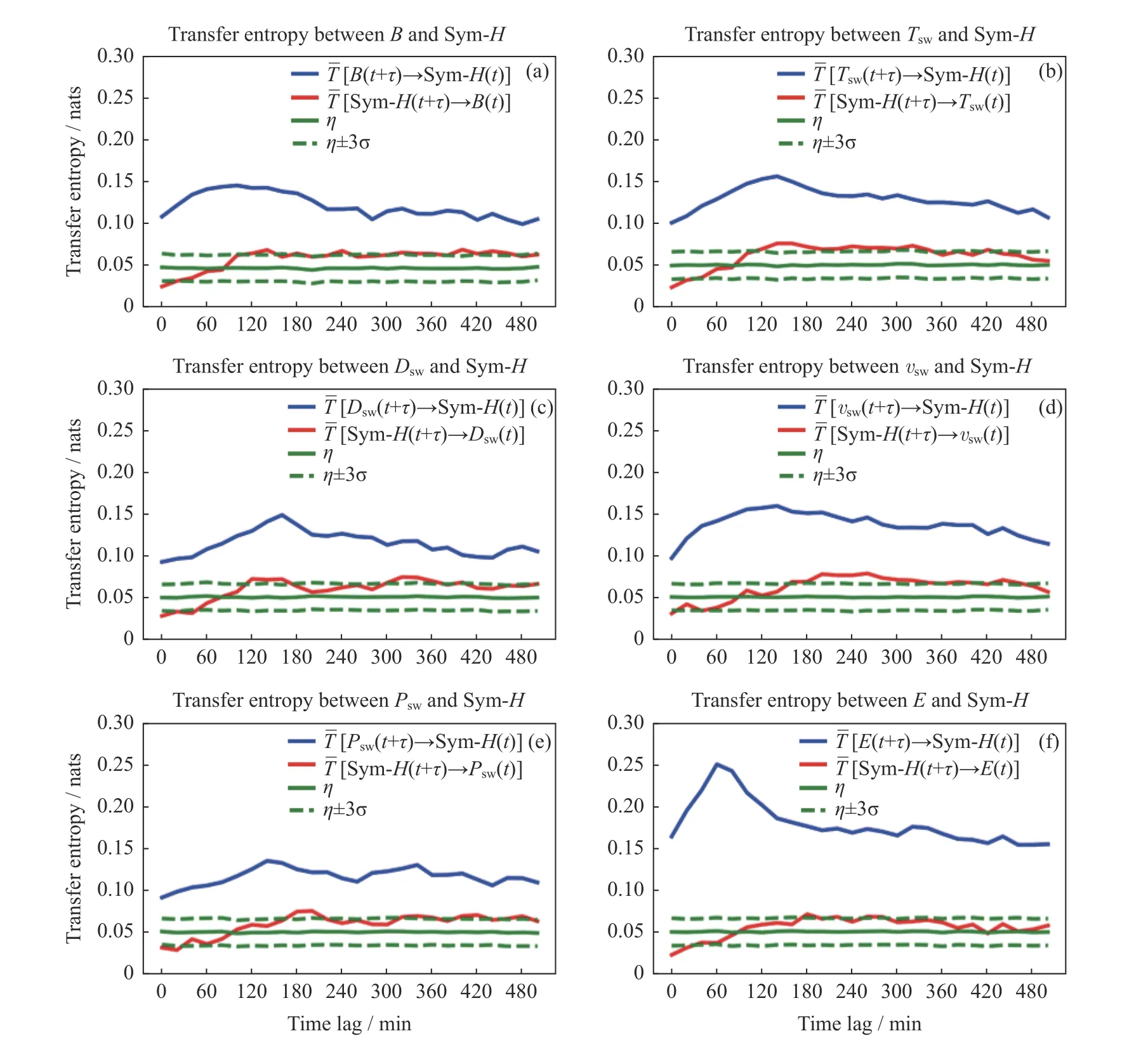
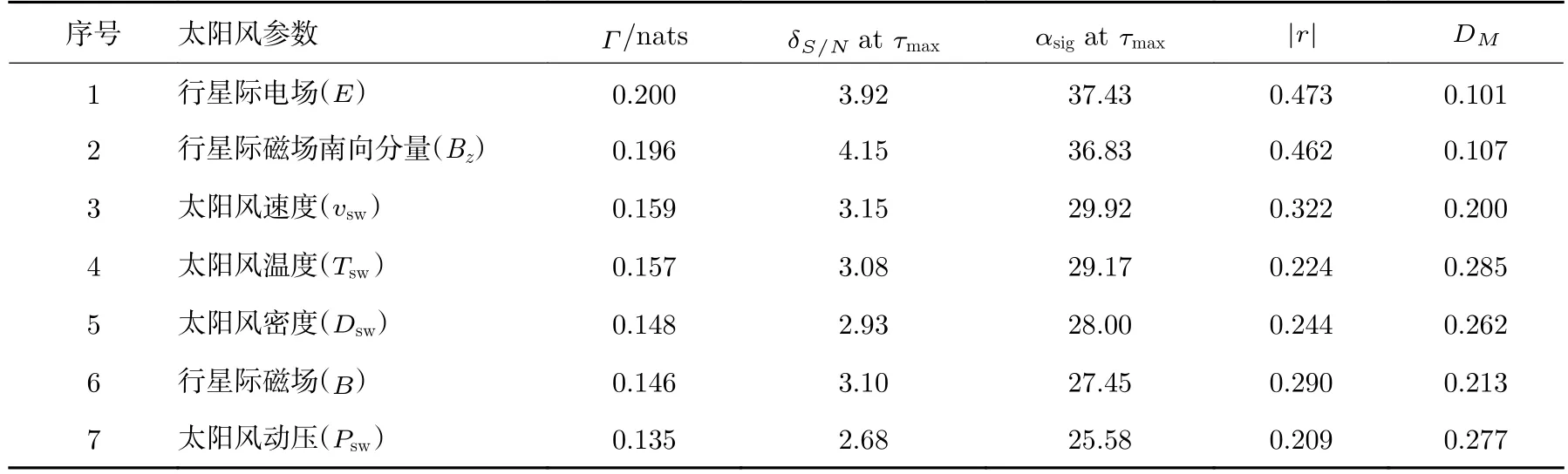
4 结论
