小天体动能撞击防御中动量传递因子敏感参数分析*

周琪 郑建华 李明涛

(中国科学院国家空间科学中心 北京 100190)

(中国科学院大学 北京 100049)

0 引言

小天体受高速动能撞击会产生很多溅射物，由于小天体引力较弱，一部分溅射物会脱离小天体引力场逃逸出去。溅射物可产生额外的推力，使得小天体的动量改变量大于撞击器的动量，小天体总动量与撞击器动量之比即为动量传递因子（β）。动量传递因子会增强小天体的偏转效果，但是受撞击器和目标小天体特性参数影响而有显著差异[1,2]。对动量传递因子影响因素开展研究，可以为动能撞击方案优化提供参考。

自1963 年以来，对各种目标小天体材料进行了大量实验室撞击实验[3,4]，以解释溅射过程，并提供溅射物碎片质量、速度、位置分布的定量测量。实验表明，溅射物性质依赖于撞击器特性参数和目标小天体的结构特性[1,5]。由于实验条件通常不能直接适用于小天体表面撞击所涉及的弱引力场、低内聚强度和较大的撞击器尺寸，因此必须利用理论模型推测相关参数值。

2011 年Housen 等[4]通过点源理论和无量纲分析建立了溅射物速度与质量分布的溅射标度律理论，通过对撞击实验数据的拟合发现不同撞击器以及目标材质下的溅射物速度与质量分布均存在幂律关系，提供了溅射物质量、速度、位置分布的理论描述。溅射物速度随与撞击位置距离的增加而减小，遵循幂律标度律，在接近撞击点附近时最大，而在接近最终撞击坑边缘时会降为零。基于该标度律，2012 年Holsapple等[1]推导计算出小天体受撞击后的β。此后，很多关于小天体动能撞击防御的研究使用这一理论估算小天体受撞击后的动量变化情况。2018 年Delchambre等[6]针对小天体的轨道确定滤波器，提出一种端到端的动量传递因子评估模型，对β的不确定性进行约束。同时，利用协方差分析和最小二乘迭代分析来评估和验证动量传递因子。Dearborn 等[7]利用LLNL开发的Spheral 软件以及LANL 开发的RAGE 软件进行数值仿真模拟，研究目标特性对动能撞击小天体产生溅射物的影响，并根据仿真结果拟合出β的另一种理论模型，给出β与撞击速度、目标孔隙率及目标表面强度三者之间的函数关系。

2013 年Walker 等[8]使用直径 4.45×10−2m 的小铝球以 2 km·s−1高速撞击直径1 m 的花岗岩球，根据溅射物的速度分布估算β，同时外推直径1 m 的铝球以1 0 km·s−1超高速撞击岩石类目标小行星表面的动量传递情况，发现撞击器尺寸的幂律达到0.4，产生的β将超过40。如此大的动量传递因子表明，动能撞击器能够非常有效地偏转单体岩石结构小行星。2015 年Hoerth 等[9]设计动能撞击实验，以不同孔隙率的岩石作为目标，计算撞击后的动量传递因子β，实验发现低孔隙率材料比高孔隙率材料产生的动量传递因子更大。2017 年Flynn 等[10]以DART 任务为背景设计了动能撞击地面实验，对不同孔隙率的岩石材料进行高速撞击，发现低孔隙率材料产生的动量传递因子比数值模拟计算结果大得多。

基于一系列初始条件开展的数值仿真研究为系统确定不同类型目标小天体表面产生的撞击效应提供了思路。2016 年Cheng 等[11]和Michel 等[12]基于NASA 的双小行星重定向测试（DART）任务，对动能撞击产生的动量传递因子进行了理论计算和数值仿真研究。2017 年Stickle 等[13]用直径6.35×10−3m的铝球或玄武岩球以 5～6 km·s−1高速撞击直径0.3m的玄武岩球，并对比CTH&Spheral软件对DART任务中动量传递因子的数值仿真结果，研究撞击角、材料微观和宏观孔隙率对动量传递因子的影响。2018 年Luther 等[14]通过数值仿真研究撞击器特性对小天体溅射物质量、速度、溅射角等的影响。2019 年Raducan 等[15]给出在均匀小行星表面进行的强度主导撞击的数值仿真，量化了目标小天体内聚力、孔隙率及内摩擦系数对动能撞击产生的溅射物质量、速度分布的影响。1968 年Quaide 等[16]通过室内实验研究目标小天体分层结构对撞击坑形成的影响，2020 年Raducan 等[17]扩展了相应研究，考虑小天体分层结构对动量传递因子的影响，量化了目标结构特性对撞击坑形态、溅射物质量、速度分布以及动量传递因子的影响。现有研究表明，动量传递因子的变化规律和撞击器特性与小天体特性参数存在相关性。

本文考虑模型适用性，选用Holsapple 等[1]给出的动量传递因子理论模型，分析撞击器特性参数（速度、半径、密度），小天体结构特性参数（小天体密度、孔隙率、表面强度、表面引力加速度等），以及标度律参数µ对β的影响，研究不同参数对动量传递因子影响的敏感性，并对不同动能撞击方案及小天体特性参数下的撞击场景进行分析，为设计和评估小天体动能撞击防御方案提供参考。

1 理论模型

2009 年Warner 等[18]给出超过5500 颗小行星自转周期与预估直径的关系[18]（见图1）。自旋界线（Spin Barrier）很明显，界线上方没有快速自转的大尺寸小行星。由引力聚积形成的小行星结构主要是由引力主导的。相反，小尺寸小行星在强度主导的区域中，可以非常快速地自转，这表明小尺寸小行星可能具有单一结构，或具有较大的内聚强度。当较大尺寸小行星达到临界自转周期（由其直径、密度、内聚强度决定）时，其将发生变形、表面物质脱落、裂变或灾难性破坏事件[19]。

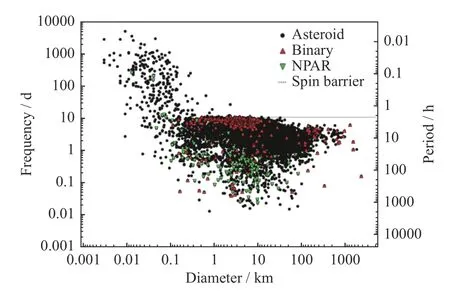
图1 超过5500 颗小行星自转周期与预估直径之间的关系Fig.1 Relationship between rotation periods and estimated diameters of more than 5500 asteroids

当质量为m的动能撞击器以速度u撞击目标小天体时，会产生大量溅射物。溅射物以一定溅射速度逃逸出小天体引力场，此时β=1+，其中pej为溅射物总动量。研究表明，动量传递因子受撞击速度、撞击器物理特性、撞击角、小天体形状、内部结构特性、自转和孔隙率等因素影响。

为简化模型，考虑采用质量为m、撞击速度为u的球形撞击器沿小天体中心线垂直撞击球形目标小行星，使用标度律模型对动量传递因子进行理论解析。标度律采用Housen 等[4]给出的形式。在引力或强度主导的情况下，分别根据常规无量纲标度律参数表示组合标度律。这里π2为引力标度律，g为小天体表面引力（单位 m·s−2），r为撞击器半径（单位m），u为撞击速度（单位 km·s−1），π3为强度标度律（材料强度与应力的比值），Y为小天体表面强度（单位kPa），ρ为小天体密度（单位 k g·m−3）。

小天体表面引力主导时，撞击坑半径

如果小天体表面强度主导，则

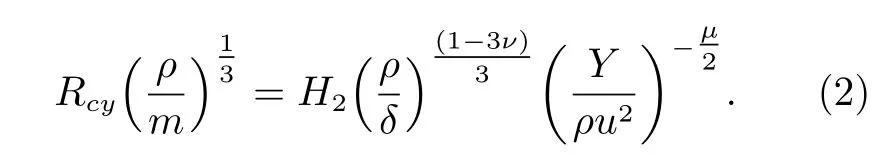
其中，δ为撞击器密度（单位 k g·m−3），m为撞击器质量（单位kg），H1、H2、µ和v为与点源理论相关的经验参数，根据点源理论耦合参数C=ruµδν，通过实验确定。

无量纲参数H1和H2为通过实验确定的每一种材料的常数，与材料特性相关。无量纲参数µ取决于小天体表面材料强度特性，其取值范围为1/3<µ<2/3，其中µ=1/3为 动量标度极限，µ=2/3为能量标度极限[20]。根据实验结果，对于干燥土壤，µ≈0.41；对于无孔材料（水、金属或岩石、玄武岩等），µ≈0.55；高度多孔材料的µ值尚未确定，但是预计小于0.4。有实验设置高度多孔材料孔隙率分别为55%、67%和83%，拟合得到µ=0.35。已有的实验结果表明，孔隙率增加对应于更接近动量标度极限的µ值，其最小取值为1/3[4]。文献[4]数据表明，不管材料类型如何，密度标度指数ν≈0.4，因此本研究中取无量纲参数ν=0.4。

在距离撞击中心点x处溅射物速度为v，有

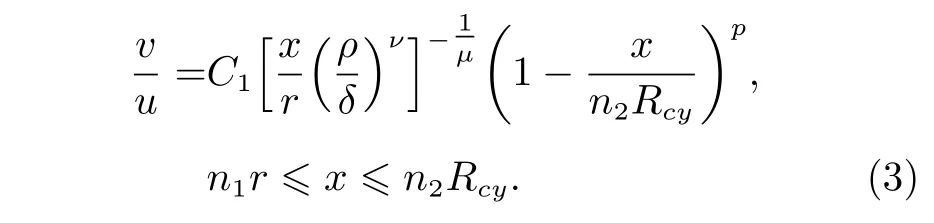
其中，C1和p为通过实验确定的每一种材料的常数，与材料特性相关。

根据式（3），在相应溅射速度以上溅射出的质量为M，有

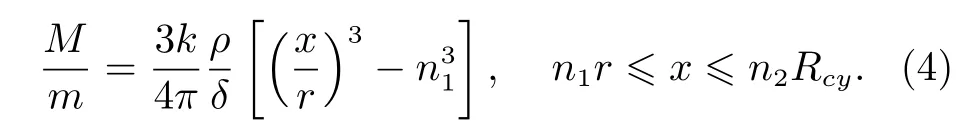
其中，k为实验室实验确定的常数。

式（3）和式（4）显示在实验室撞击实验中得到的溅射速度分布：在高溅射速度下，x=n1r处溅射物质量为零；在低溅射速度下，x=n2Rcy处溅射速度为零。

在径向距离dx内溅射出的溅射物质量为

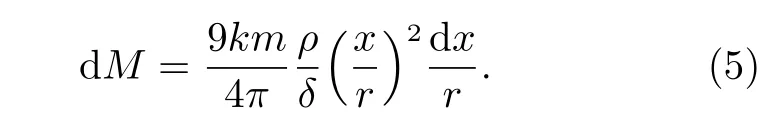
溅射物在无穷远处的动量为vinfcosθdM。这里vinf为无穷远处的速度，其中vinf=0表 示低于逃逸速度，θ表示溅射角。由于实验室撞击实验中观察到目标靶的溅射角约为45°[21]，这里以溅射角为45°开展研究。

通过对w=x/r积分，可以得到溅射物溅射至无穷远处的总动量为[1]

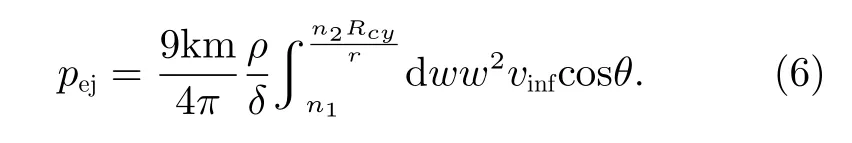
其中，ur=v/vesc，这里v为 溅射物速度，vesc为小天体表面逃逸速度。可得偏心率为e的双曲线溅射轨迹，有

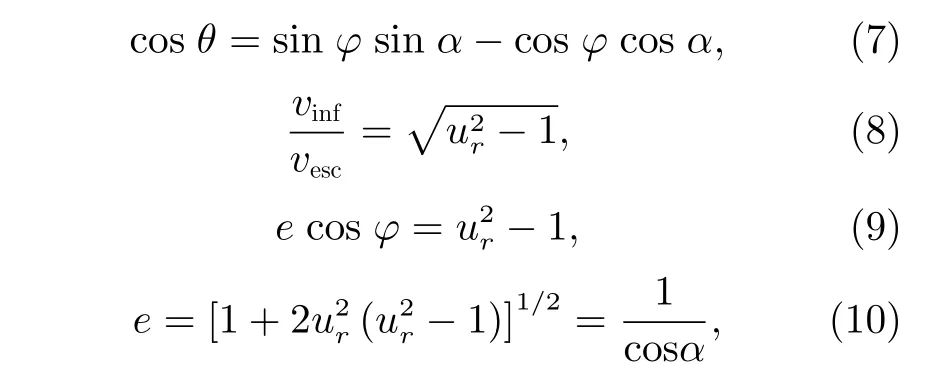
则动量传递因子为

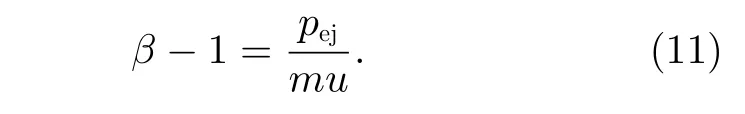
通过实验室实验数据观测，可以得出式（3）的近似表示[1]，即

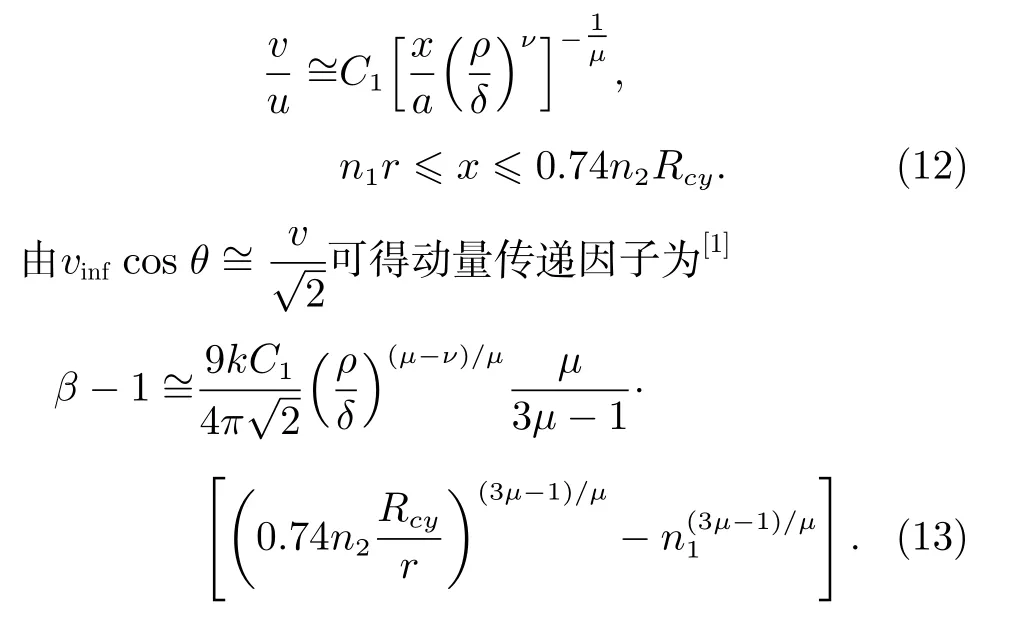
式（13）中的系数0.74 是通过对式（6）进行数值积分拟合得到的。如果忽略式（13）中括号内最后一项，利用式（2）可得[1]

对于高度多孔的目标小天体材料，参数µ可能接近1/3。另外，动能撞击产生的动量传递因子β大小还取决于撞击角和目标结构，在随后的数值仿真中将讨论其影响。

2 动量传递因子的参数敏感性

根据第1 节介绍的动量传递因子理论模型，对模型公式进行参数敏感性分析，找出各参数对动量传递因子的影响规律。

目标材料类型一直是动能撞击效应相关研究的核心因素之一。2007 年Richardson 等[22]取Holsapple在1993 年给出的材料类型——砂、湿土、干土、软石块和硬石块等，重建了撞击溅射模型，对比深度撞击任务观测结果，精确评估9 P/Tempel 1 彗星的表面引力、质量和密度。同时，Holsapple 等[23]取Richardson等在2005 年给出的材料类型，即粗砂和不同强度的粘性土壤以及软石块等，建立撞击坑及溅射物的分布模型，对比观测结果，解释深度撞击任务的撞击效应。Ernst 等[24]根据9 P/Tempel 1 彗星材料特性，选择不同材料类型——浮石、珍珠岩、白云石等，评估材料类型对撞击闪光演化的影响。2010 年Hermalyn等[25]在NASA 艾姆斯研究中心垂直射击场（AVGR）采用空心铝球撞击20#～30#砂和浮石靶材，与此前研究进行比对，以更好地解释撞击参数对2009 年LCROSS 撞击任务中撞击月球陨石坑产生的早期溅射物分布的影响，对溅射物速度分布的时间和热力学演化进行测量，评估不同溅射物组分的质量分布、溅射角度分布以及撞击坑深度。2017 年Arakawa 等[21]针对Ryugu 小行星探测任务中的SCI（Small Carryon Impactor）撞击模块，首次预设Ryugu 小行星表面可能存在的7 种材料类型，按照材料颗粒层直径分类，同时给出预期撞击坑直径和适用的主导律（引力主导或强度主导）。

2020 年Cheng 等[26,27]给出DART 任务分析动量传递因子时使用的材料类型（见表1）[4]。对表1 中材料结构进行敏感性分析。表1 给出的材料结构经验参数是基于实验室中溅射物分布实验数据得到的，5 种材料类型分别对应小天体不同类型结构：石块材料结构对应单体岩石结构小天体，粗砂、弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物四种材料结构对应碎石堆结构小天体。

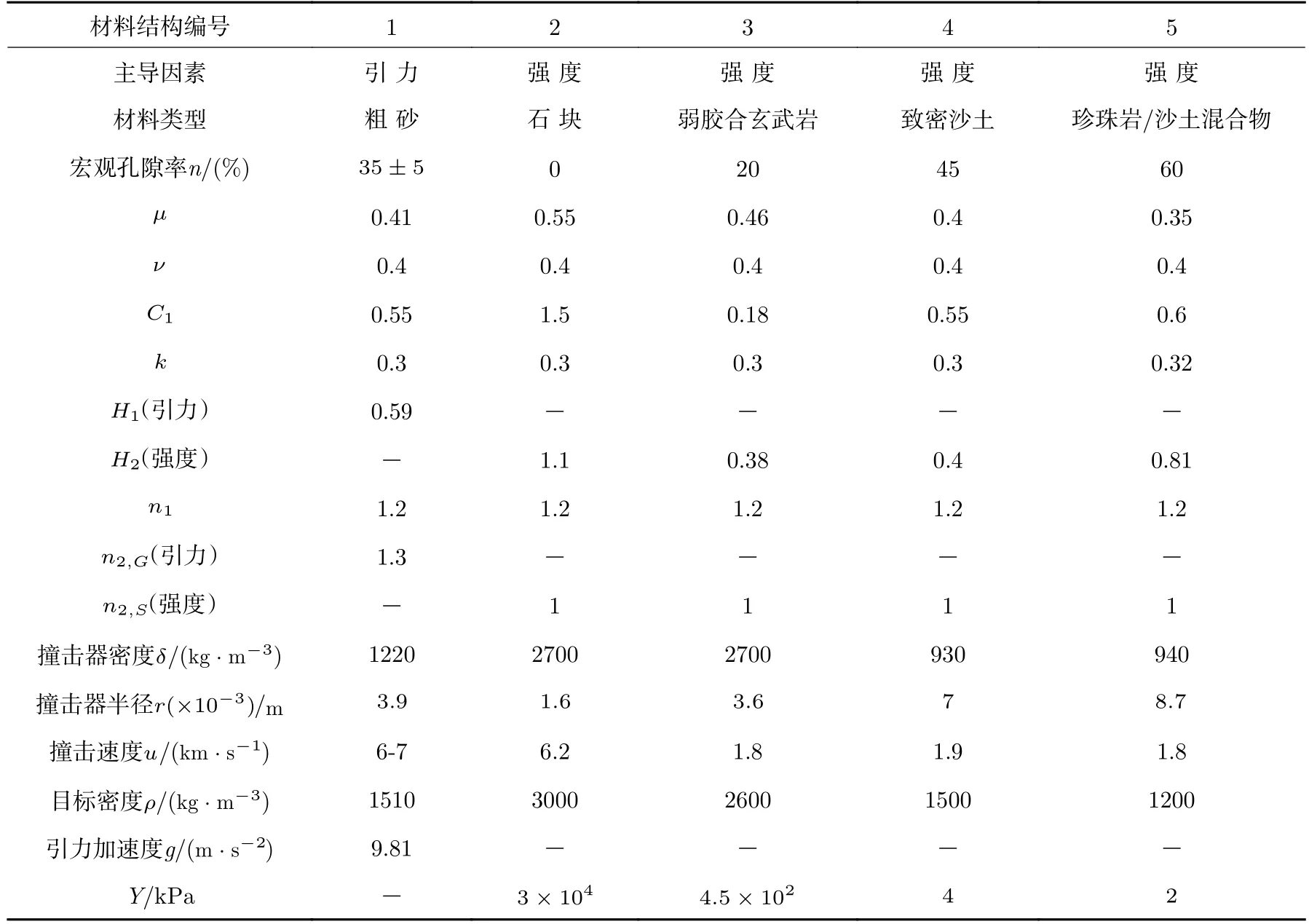
表1 可参考的材料经验参数Table 1 Experience parameters of materials

图2 给出了小天体5 种类型表面的典型图像[21]。将直径大于1.5 m 的岩石设定为单体石块，设置的撞击体无法完全破坏该石块，其可能在石块上形成一个简单的撞击坑，或部分破坏石块，单体石块上所形成的撞击坑属于强度主导。颗粒层是颗粒直径在1×10–3～1.5×10–1m 的层。颗粒层中包含：弱胶合玄武岩，粒径为5×10–2～1.5×10–1m；粗砂，粒径为1×10–3～5×10–2m。最后，细颗粒层是颗粒直径小于1×10–3m的层。细颗粒层中包含：致密沙土，孔隙率为40%～45%；珍珠岩/沙土混合物，孔隙率为60%。这5 种类型的表面结构合理涵盖了小天体可能的表面结构范围。因此，这里在考虑这5 种结构材料情况下对撞击坑的成坑规律和动量传递规律进行参数敏感性研究。

图2 小天体表面的5 种类型Fig.2 Five types of surfaces of small bodies

按上述动量传递因子模型，分别考虑引力主导和强度主导对动量传递因子形成规律进行分析。在参数敏感性分析时，需要考虑诸多因素，为此建立了参数取值范围（见表2），开展参数对动量传递因子的影响规律分析。

表2 特性参数可取值范围Table 2 Range of property parameters

图3 给出了引力主导时，各参数分别提升一个数量级后，动量传递因子的形成规律。由图3 可知，小天体为碎石堆结构时，小天体撞击效应为引力主导，动量传递因子对撞击器特性参数与小天体特性参数均不敏感，并且动量传递因子取值较低。在标称情况下，β≈1.8177。

从图3 可以看出：撞击器密度提升1 个数量级，粗砂结构中β提升22.53%，撞击器密度对β取值不敏感；撞击器半径提升1 个量级，粗砂结构中β降低11.30%，撞击器半径对β取值不敏感；撞击速度提升1 个量级，粗砂结构中β提升25.16%，撞击速度对β取值不敏感；小天体引力加速度提升1 个量级，β降低16.07%，小天体引力加速度对β取值不敏感；小天体密度提升1 个量级，粗砂结构中β取值降低了18.42%，小天体密度对β取值不敏感；按参数µ取值范围，1/3<µ<2/3，粗砂结构中β取值产生了1 个量级的提升，可以看出目标材料相关参数µ对β取值极敏感。

图3 引力主导时动量传递因子随各参数的分布（材质孔隙率30%～40%）Fig.3 Distribution of momentum transfer factor β with each parameter when gravity dominates (Porosity of the material is between 30% and 40%)

图4 给出了强度主导时，各参数分别提升1 个数量级后动量传递因子的形成规律。由图4 可知，强度主导时，石块（约0%）、弱胶合玄武岩（20%）、致密沙土（45%）、珍珠岩/沙土混合物（60%）四种材料结构形成的动量传递因子变化规律相似。相比后三种碎石堆结构，单体岩石结构形成的动量传递因子取值变化比较显著；小天体为碎石堆结构时，动量传递因子对撞击器特性参数与小天体特性参数均不敏感。

图4 显示，当撞击器密度提升1 个数量级时，石块、弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物等四种材料结构中β分别提升了54.7%、5.44%、17.31%、17.87%，石块结构中β取值提升幅度较大，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种碎石堆结构中β取值提升幅度较小。撞击器密度在小天体为单体岩石结构时对β取值较敏感，在小天体为碎石堆结构时对β取值不敏感。强度主导时，撞击器半径与β不相关，其对β取值不敏感。当撞击速度提升1 个量级时，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种碎石堆结构中β分别提升11.96%、18.53%、8.96%，提升幅度较小，而石块结构中β取值提升幅度较大，提升了2.1033 倍。撞击速度在小天体为单体岩石结构时对β取值敏感，在小天体为碎石堆结构时对β取值不敏感。当小天体表面内聚强度提升6 个量级，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种碎石堆结构中β取值降低幅度较小，分别为22.35%、24.39%、23.14%，石块结构中β取值降低幅度很大，下降了95.10%。小天体表面内聚强度在小天体为单体岩石结构时对β取值敏感，在小天体为碎石堆结构时对β取值不敏感。当小天体密度提升1 个量级，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种碎石堆结构中β取值降低幅度较小，分别为22.35%、24.39%、23.14%，石块结构中β取值降低幅度很大，下降了95.10%。小天体密度在小天体为单体岩石结构时对β取值极敏感，在小天体为碎石堆结构时对β取值不敏感。同时，石块结构中的β取值比碎石堆结构中β取值大得多，这也意味着动能撞击防御单体岩石结构小天体取得的预期效果将比碎石堆结构小天体要好得多。按参数µ取值范围，1/3<µ<2/3，石块、致密沙土、珍珠岩/沙土混合物三种材料结构中β取值均产生了1 个量级的提升，弱胶合玄武岩材料结构（孔隙率为20%）中β取值提升幅度较小，为71.12%。综上可得，材料相关参数µ对β取值极敏感。

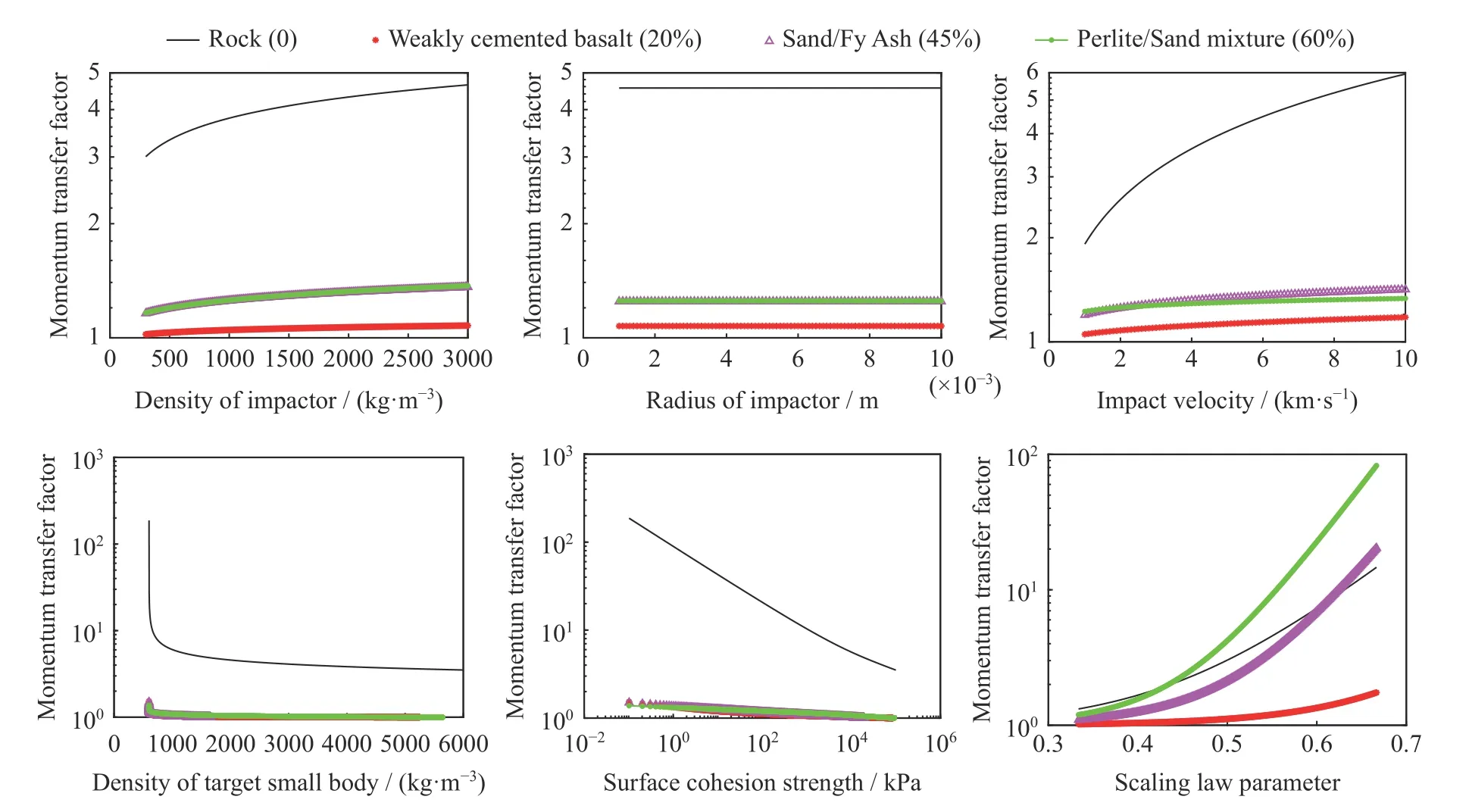
图4 强度主导时动量传递因子随各参数的分布Fig.4 Distribution of momentum transfer factor β with each parameter when strength dominates

对比图3 与图4 可以发现，无论引力主导还是强度主导，撞击器密度、撞击速度和参数µ与动量传递因子成正相关，小天体引力加速度、小天体表面内聚强度和小天体密度与动量传递因子负相关；在引力主导时，撞击器半径与动量传递因子负相关；在强度主导时，动量传递因子β的形成与撞击器半径无相关性。各参数与动量传递因子的相关性列于表3。

表3 引力/强度主导时参数与动量传递因子相关性Table 3 Correlation between parameters and momentum transfer factor when gravity/strength dominates

3 小天体防御动能撞击效应

3.1 不同动能撞击方案撞击小天体产生的撞击效应

以Apophis 小行星作为动能撞击目标，进行不同动能撞击方案产生的撞击效应分析，相关参数列于表4[34,35]。分别选择表1 中的石块、粗砂（引力主导）、弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物5 种材料结构作为Apophis 小行星可参考的结构类型。动能撞击效应包括撞击坑半径和撞击坑深度的成坑效应[36]以及动量传递因子。

表4 Apophis 小行星参数Table 4 Parameters of Apophis asteroid

参考文献[28，29]中给出的动能撞击方案进行分析，动能撞击方案具体参数列于表5。

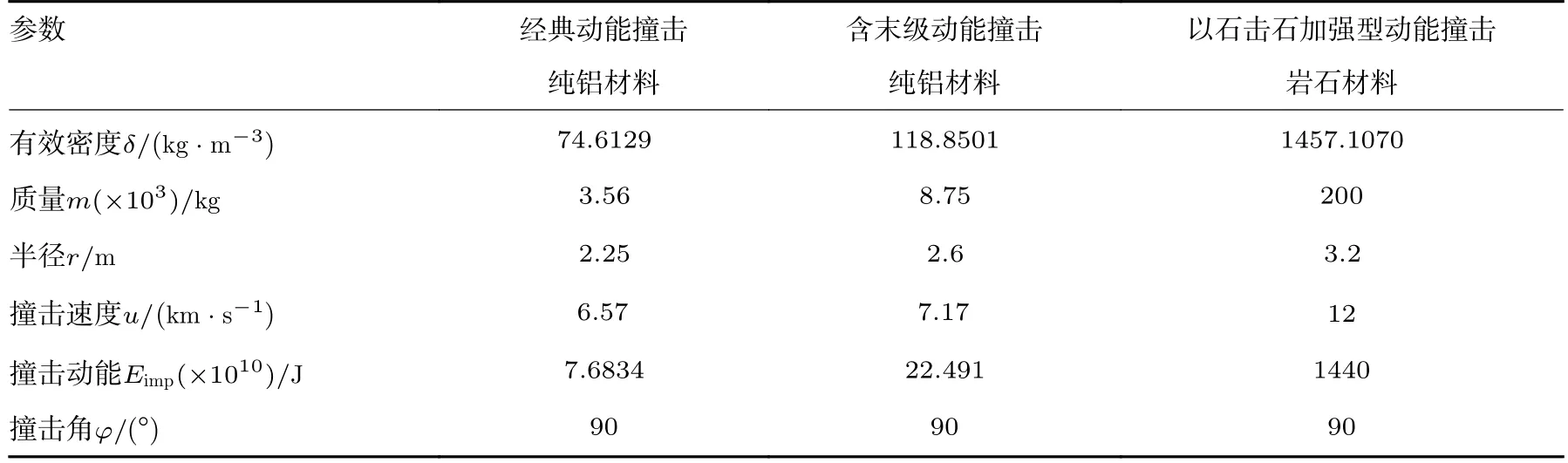
表5 三种不同动能撞击器参数Table 5 Parameters for kinetic impactors of three types

（1）经典动能撞击方案（Classic Kinetic Impact，CKI）：发射一颗无人航天器，以高速撞击危地小天体，偏转其轨道。

（2）含末级动能撞击方案（Assembled Kinetic Impact，AKI）：2020 年Wang 等[28]提出将航天器与火箭末级作为组合撞击器的新型动能撞击概念，即火箭末级将航天器送入地球逃逸轨道后，不实施星箭分离，航天器操控航天器与火箭末级组合撞击体撞击危地小天体，充分利用火箭末级的质量，提升撞击器在撞击小天体时的质量，显著改变小天体的动量，进而偏转小天体的轨道。

（3）以石击石加强型动能撞击方案（Enhanced Kinetic Impact,EKI）：2020 年Li 等[29]提出，发射一颗无人航天器，捕获一颗百吨级质量的小尺寸小天体或者从大尺寸小天体上采集百吨级质量的岩石，高速撞击大尺寸危地小天体，显著偏转其轨道。

根据仿真计算，三种不同动能撞击方案的成坑效应与动量传递因子的比较分别见图4 和图5。

由图5 可以看出，引力标度律主导时，三种撞击方案中，以石击石加强型动能撞击产生的成坑效应是最显著的。对于撞击坑半径和撞击坑深度两个指标，末级动能撞击只在经典撞击的基础上提升了35.56%，而以石击石加强型动能撞击产生的撞击坑半径超过了小行星半径，可以认为加强型动能撞击能够将Apophis 小行星撞碎。对于动量传递因子，末级动能撞击只在经典动能撞击的基础上提升了4.42%，而以石击石提升了40.65%。以石击石方案中撞击器质量为经典动能撞击方案中撞击器质量的56 倍，以石击石撞击器的初始动能是经典动能撞击器初始动能的近187 倍，由此推断，撞击器初始动能对动量传递因子影响较大。

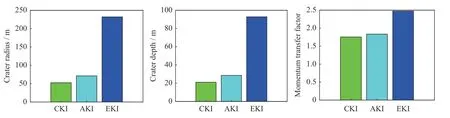
图5 引力主导时三种不同动能撞击方案的成坑效应与动量传递因子Fig.5 Cratering effects and momentum transfer factors for kinetic impact schemes of three types when gravity dominates

图6 显示，强度标度律主导时，三种动能撞击方案产生的成坑效应与引力主导时相似，以石击石加强型动能撞击产生的撞击坑半径和撞击坑深度数值较大。而横向比较时，小天体若是碎石堆结构，可以看出，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种结构孔隙率逐步提升，而对应的动能撞击产生的撞击坑半径和撞击坑深度数值也在不断升高。这表明，小天体结构孔隙率对撞击坑尺寸影响较大。对单体岩石结构，其对应的动能撞击产生的撞击坑尺寸与孔隙率为45%的致密沙土结构基本一致，其原因尚不明确，有待开展进一步的数值仿真研究。同时，弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物三种碎石堆结构对应的动量传递因子基本不变，对动量传递因子形成规律表现出较强的一致性。对于单体岩石结构，其对应的动量传递因子取值较大，与碎石堆结构表现出的规律特性明显不同，该结论与第2 节中参数敏感性分析得出的结论一致。

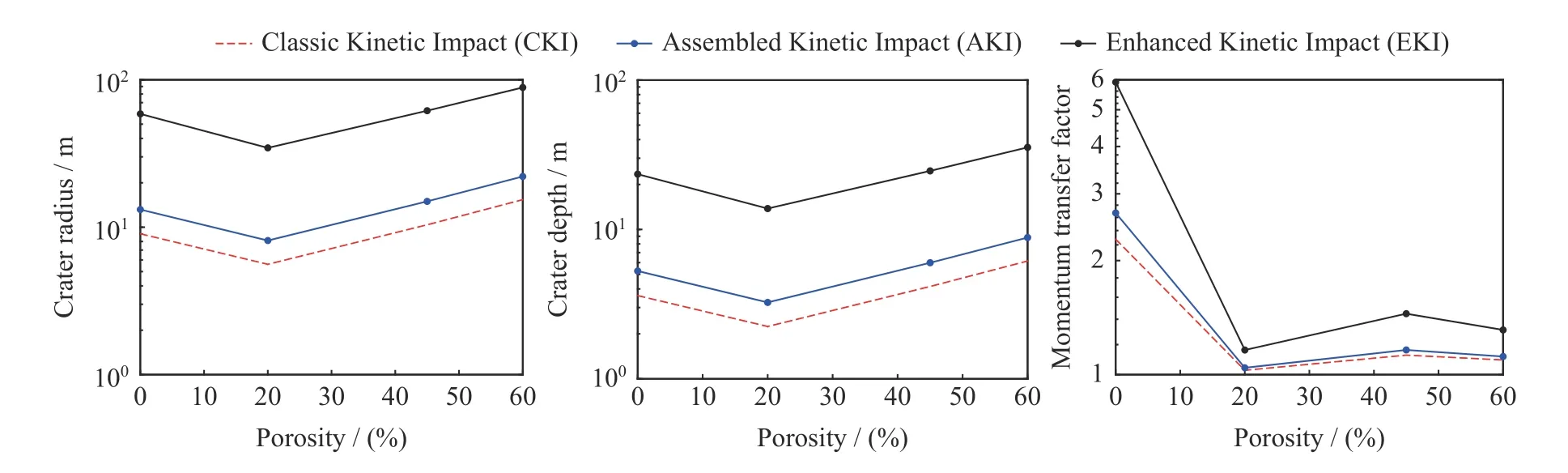
图6 强度主导时三种不同动能撞击方案的成坑效应与动量传递因子Fig.6 Cratering effects and momentum transfer factors for kinetic impact schemes of three types when strength dominates

3.2 对不同材料特性小天体采取相同动能撞击方案产生的撞击效应

这里，选择Ryugu 小行星（C 型）[37-39]、Apophis小行星（S 型）[34,35]以及1950 DA 小行星（X 型）[40-42]作为动能撞击目标小天体，对应小行星的相关特性参数列于表6。分别选择表1 中的粗砂（引力主导）、弱胶合玄武岩、致密沙土、珍珠岩/沙土混合物4 种材料结构作为目标小天体参考结构类型。同时，选择含末级动能撞击方案，进行相同动能撞击方案产生的撞击效应分析，如图7 和图8 所示。

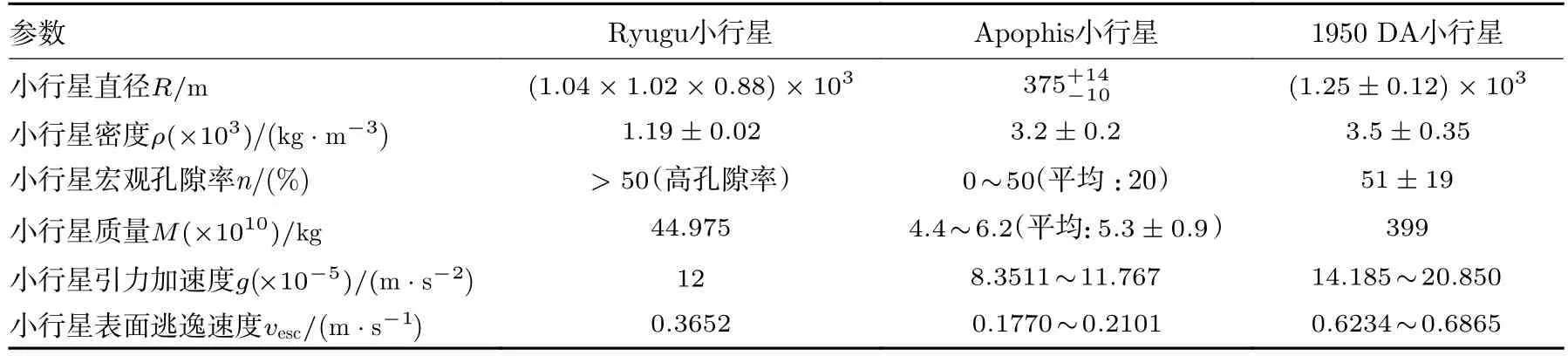
表6 不同类型小行星参数Table 6 Parameters for asteroids of different types

从图7 和图8 可以看出，末级动能撞击不同类型小行星，产生的撞击坑尺寸排序为：Rcy,C>Rcy,S>Rcy,X，Hcy,C>Hcy,S>Hcy,X。这三种类型小行星对应的动量传递因子，在引力主导时，βC>βS>βX，而在强度主导时基本相同。对于Ryugu 小行星（C 型），隼鸟二号探测器在龙宫小行星表面撞击产生了一个直径17.6 m 左右的撞击坑，探测结果表明Ryugu 小行星表面是引力主导成坑的。而对于Apophis 小行星（S 型）和1950 DA 小行星（X 型），尚不明确是引力主导还是强度主导成坑的。

图7 引力主导时末级动能撞击三种不同类型小行星的撞击效应指标Fig.7 Index of impact effects for asteroids of three different types with final kinetic impact when gravity dominates

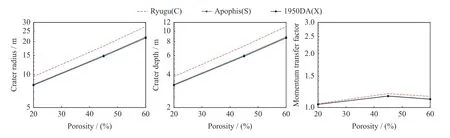
图8 强度主导时末级动能撞击三种不同类型小行星的撞击效应指标Fig.8 Index of impact effects for asteroids of three different types with final kinetic impact when strength dominates

4 结论

依据动量传递因子的理论模型开展参数敏感性研究，结果表明，参数µ对动量传递因子取值极为敏感，影响较大。当小天体为单体岩石结构时，撞击器的速度和密度以及小天体的密度和表面强度对动量传递因子影响较大，而撞击器半径和小天体引力加速度对动量传递因子影响较小。当小天体为碎石堆结构时，动量传递因子对撞击器特性参数及小天体特性参数不敏感，且数值较小。

依据理论模型，对三种不同动能撞击方案的撞击坑尺寸与动量传递因子形成规律进行研究，发现撞击器初始动能对动量传递因子影响较大，小天体结构孔隙率对撞击坑尺寸影响较大。同时，对于单体岩石结构，其对应的动量传递因子取值较大，而碎石堆结构对应的动量传递因子取值较小，且在三种碎石堆结构中基本保持不变。此外，以石击石加强型动能撞击产生的撞击效应显著，具有较好的动能防御优势。

对于相同末级动能撞击方案下不同材料特性小行星（C 型、S 型和X 型）产生的撞击效应进行分析，发现用末级动能撞击不同材料特性小行星，其产生的撞击坑尺寸排序为Rcy,C>Rcy,S>Rcy,X，Hcy,C>Hcy,S>Hcy,X。这三种材料特性小行星对应的动量传递因子，在引力主导时，βC>βS>βX，而在强度主导时取值较小，且基本相同。

本文以动量传递因子理论模型开展参数敏感性研究，对动能撞击防御场景的应用，为后续利用数值仿真模型研究动量传递因子提供了理论依据，并为设计和评估高效的动能撞击防御小天体方案提供参考。