非标准托盘尺寸优化设计系统的开发

宋卫生，薛阳

非标准托盘尺寸优化设计系统的开发

宋卫生，薛阳

（河南牧业经济学院，郑州 450046）

开发一款非标准托盘尺寸优化设计系统，用以提高物流效率，降低物流成本。使用托盘装载货物的平面利用率和装入运输工具的空间利用率进行双重约束，采用简单重叠式、正反交错式、纵横交错式、旋转交错式4种方式进行堆码，以单车装货量最高为优化目标构建优化算法。在此基础上设计优化系统，并进行算例验证。按文中算例所给数据可得，最优的托盘尺寸为1 200 mm× 1 029 mm，对应的装载方式为正反交错。该系统具有一定的实用价值，但是还存在堆码装载物体形状以及堆码方式考虑不足的问题，还有进一步提升的空间。

非标准；托盘尺寸；优化设计

依照托盘的规格可将托盘分为标准托盘和非标准托盘[1-2]。标准化托盘可以提高货架、运输车辆，物流设施以及集装箱的尺寸对接效果，从而提高物流效率，降低物流成本[3]。我国托盘的规格来自欧洲、亚洲、美国等国家的托盘标准，各行业也有自己的托盘标准，这些因素使得我国目前有超过100种托盘尺寸，因此，很难将托盘尺寸统一为标准托盘尺寸[4]。

国内对标准托盘尺寸系统的研究较多，而对非标准托盘尺寸优化设计系统的研究较少。根据国外调查的经验，非标托盘在整个市场也应占一部分。据不完全统计，国内市场当前流通的托盘仍有70%为非标准托盘[5]，主要原因有2个，首先是企业生产的产品种类比较多，在生产过程中注重产品包装设计，并不太考虑产品与物流托盘的尺寸是否匹配的问题。其次是企业使用统一标准化托盘，不仅需要物流单元配套的设施设备，还要重组供应商和客户的业务流程，这都会给企业带来额外的投资成本[6-8]。目前，国内在非标准托盘尺寸优化设计方面的研究较少，已有的研究也存在约束考虑不够全面的问题[9-11]，因此非标准托盘的尺寸优化设计是一个非常值得研究的课题。文中在采用简单重叠式、正反交错式、纵横交错式、旋转交错式4种堆码方式的基础上，以长方体货物为装载对象，同时考虑托盘装载货物的平面利用率以及装入运输工具的空间利用率这两方面的双重约束，对托盘尺寸进行优化[12]。

1 非标准托盘尺寸优化流程

1.1 信息输入

如图1所示，基于托盘装载平面利用率以及运输工具装载的空间利用率双重约束的考虑，优化系统需要的基本信息为运输工具的长度Y、宽度Y、高度y，货物包装箱的长度b、宽度b、高度b。为了使得优化尺寸更加切合实际，需要根据经验与实际情况确定非标准托盘的最大尺寸max、最小尺寸min和高度t。

最小尺寸min可以按照4种典型堆码方式托盘装载最少时的尺寸并结合托盘装卸设备对托盘的尺寸要求来确定最小尺寸，最大尺寸max可以根据车辆的尺寸以及装卸的方便性、稳定性来具体确定。托盘高度t按照行业的不同需要，常见的有140、150、160、170 cm几种规格，企业可以根据自己的情况进行选择。

1.2 整理优化设计流程

首先根据运输工具的长Y、宽Y以及非标准托盘的最大尺寸max、最小尺寸min计算得出托盘在车厢内长度方向所能排列的极限数量1、2，以及宽度方向所能排列的极限数量1、2。

以长、宽方向的最小数量2、2为初始值，以最大数量1、1为最大边界值进行双重for循环。依次计算在不同长度方向排列数量和宽度方向排列数量组合条件下的托盘尺寸1和2，定义所得托盘尺寸的最大值为托盘长T，最小值为托盘宽T结合货物包装箱的长B、宽B，以简单重叠式、正反交错式、纵横交错式、旋转交错式等4种为托盘堆码方式进行优化。

由于简单重叠式堆码与纵横交错式堆码单层的计算流程相同，所以将优化装载流程可分为3个部分，分别为简单重叠式及纵横交错式堆码优化流程、正反交错式堆码优化流程和旋转交错式堆码优化流程。通过优化可以得到在当前托盘尺寸条件下，每种堆码方式对应的托盘单层最大堆码数量，此时，车厢长度排列托盘数量为，宽度排列托盘数量为，根据纸箱高B、托盘高T以及车厢高Y的尺寸可得高度方向可装载纸箱数量n的计算见式（1）。

根据以上信息可得，在目前情况下，车厢内最高的纸箱装载数量的计算见式（2）。

不同的和均能优化得出车厢内最高的纸箱装载数量，车厢装载率最高是文中系统的优化目标之一，因此每种托盘堆码方式均能得到一个最大的值，值与单件物品重量d的乘积应小于车辆的最高载重，那么这个值就是在该托盘堆码方式以及最佳的托盘尺寸情况下，车厢的最高装载数量。此时所对应的托盘最优尺寸、托盘堆码参数、车厢装载方式均可获得。由于装载稳定性较难定量描述，最后需要设计人员综合各方案对应的装载数量与堆码稳定性得出最优方案[13]。

2 托盘装载优化流程

2.1 简单重叠式及纵横交错式装载优化流程

简单重叠式及纵横交错式装载优化的流程见图2，首先以箱长对托盘长和箱长对托盘宽2种不同的排列方式进行计算，分别得出最佳排列数量，然后进行比较，数量最大者所对应的排列方式即为最优方案，如果两者不相等，则无法按照纵横交错的形式进行堆码，如果两者相等，为了提高装载的稳定性，就需要按照纵横交错的形式进行堆码。

2.2 正反交错式装载优化流程

正反交错式装载优化的流程见图3，托盘的装载分为以下2种方式，第1种方法是纵横临界线与托盘长方向垂直，见图4，以箱宽对托盘宽的行数1为操纵变量，箱长对托盘宽的行数为被控变量，其中1的取值范围为托盘长减去一个纸箱宽，剩余长度所能排列纸箱长的数量。第2种方法是纵横临界线与托盘宽方向垂直，见图5，以箱宽对托盘长的行数2为操纵变量，箱长对托盘长的行数为被控变量，其中2的取值范围为托盘宽减去一个纸箱宽，剩余长度所能排列纸箱长的数量。

在优化过程中为避免出现第2层无法堆垛的情况，需要排除以上两图中纸箱横向排列的间隙大于纸箱宽度的情况，图3的限定条件为式（3），图4的限定条件为式（4）。

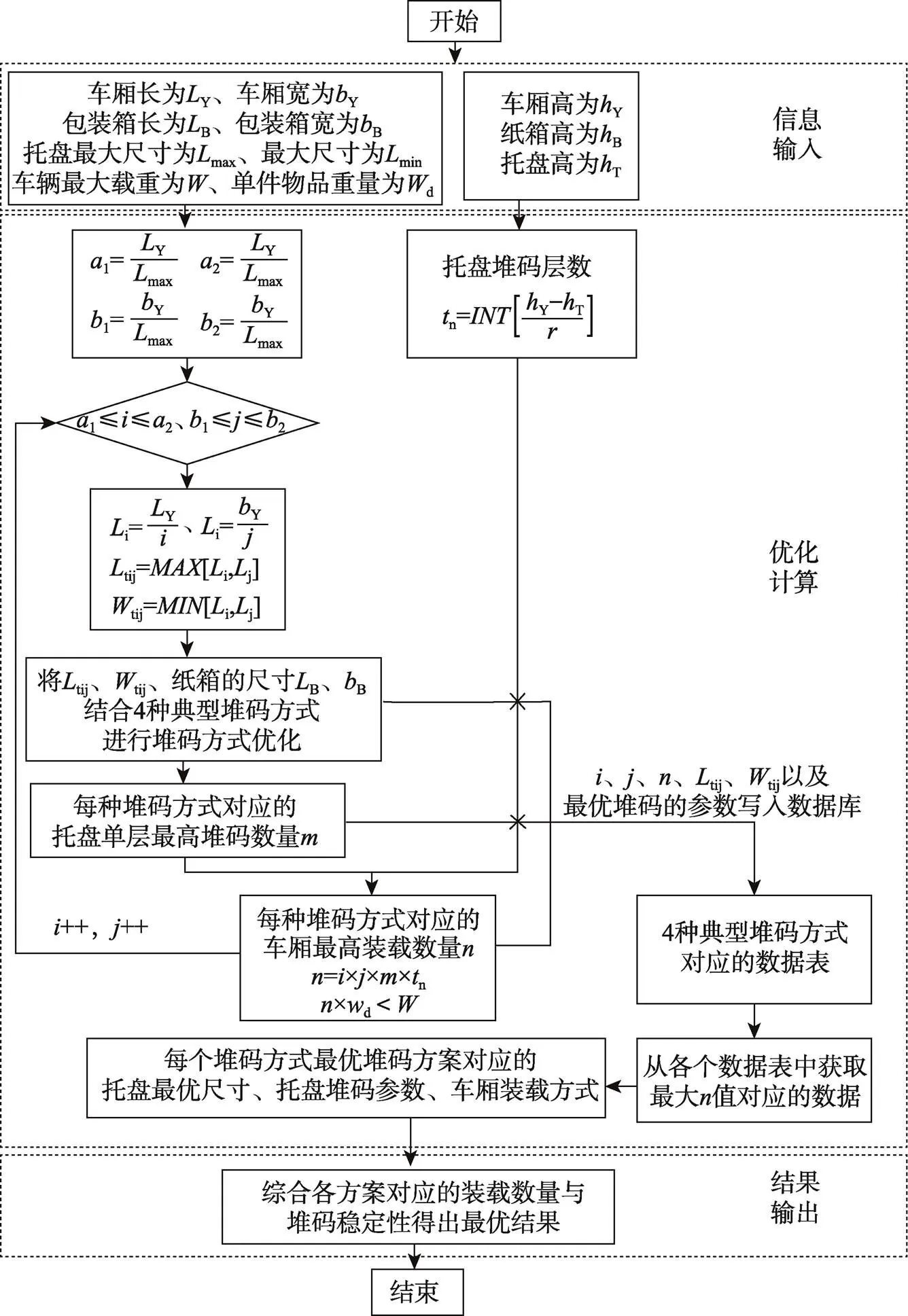
图1 非标准托盘尺寸优化流程

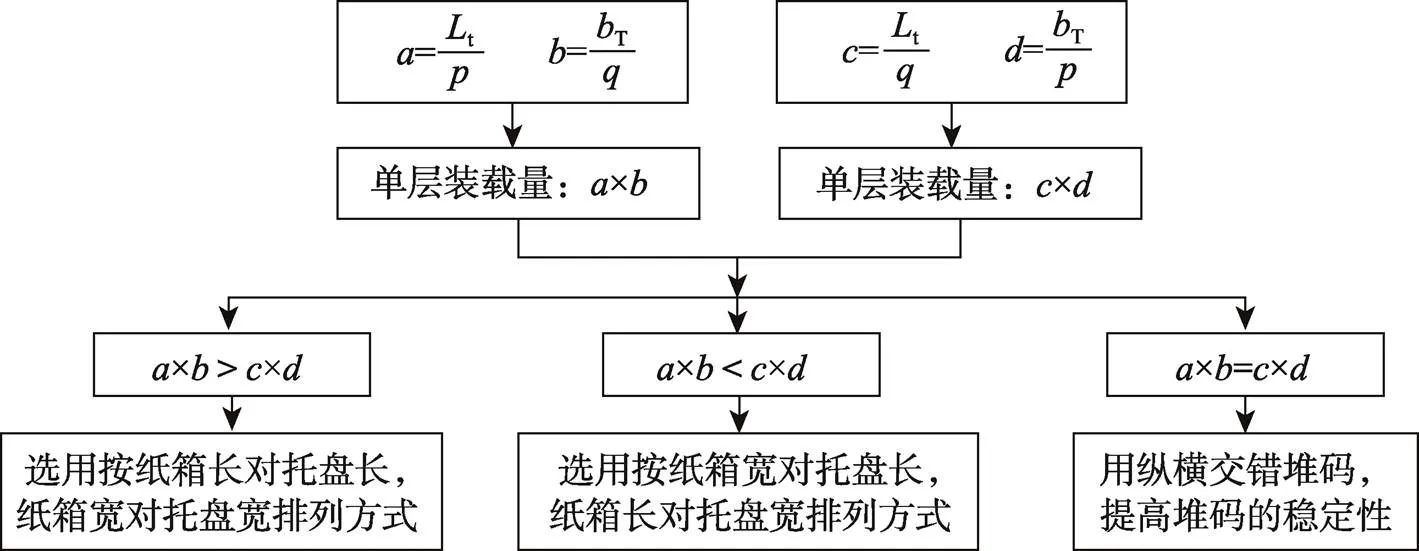
图2 简单重叠式及纵横交错式装载优化流程

图3 正反交错堆码优化流程

图4 正反交错装载方式1

图5 正反交错装载方式2

在for循环中变化1或2，可以得到多种不同的排列方式，单层排列数量计算方法见图5。取排列数量最多者为最优方案。

2.3 旋转交错式装载优化流程

旋转交错式装载优化见图6，旋转交错式装载优化流程见图7。根据旋转交错装载方式与角排列方式相同的特点，只需利用for循环对上下或左右相邻两角进行优化排列即可，图6中的1、2、3、4为相邻两角纵横向的排列数量。

图6 旋转交错堆码示意

为了排除对角排列的包装箱在中心处交叉重叠，需要设定限定条件见式（5）或式（6）。

单层总排列数量见式（7），3和4的含义见式（8）和式（9）。

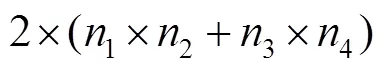
其中：

式中：为托盘长度；为箱子长度；为托盘宽度；为箱子宽度；n1、n2、n3、n4分别为箱体在托盘上不同方向的排列数量，见图6。

通过for循环可以得到多个单层排列数量结果，取排列数量最大者为最优方案。

3 软件运行实例

选用托盘尺寸为800～1 300 mm，确定纸箱尺寸为400 mm×300 mm×300 mm，确定车厢尺寸为17 500 mm× 2 400 mm×2 700 mm。

3.1 信息输入

在如图8所示的输入窗口填写托盘最小尺寸为800 mm，托盘最大尺寸为1 300 mm，确定纸箱长度为400 mm，宽度为300 mm，高度为300 mm，确定车厢长度为17 500 mm，宽度为2 400 mm，高度为2 700 mm，车辆的最大载质量为35 000 kg，单件包装质量为10 kg，设定数据后进行提交。系统输入页面见图8。

3.2 结果输出

系统的结果输出界面以简单重叠式堆码、正反交错式堆码以及旋转交错式堆码3个模块进行显示。在3个模块中分别给出托盘尺寸的优化结果，同时也给出了车厢总排列数量以便于比较选择堆码方式，为了便于操作，也给出了托盘在车厢内的排列数量，为了便于记忆，将纸箱尺寸以及车厢尺寸一并在此显示。模块最后一行“点击查看托盘堆码方式”，这是一个链接，可以链接另一个程序，以图形的方式查看当为简单重叠式堆码时，单托盘单层纸箱排列方式，图片中心以数字的形式显示了单托盘单层装载量。输入参数后的输出界面以及前文算例的优化结果见图9。

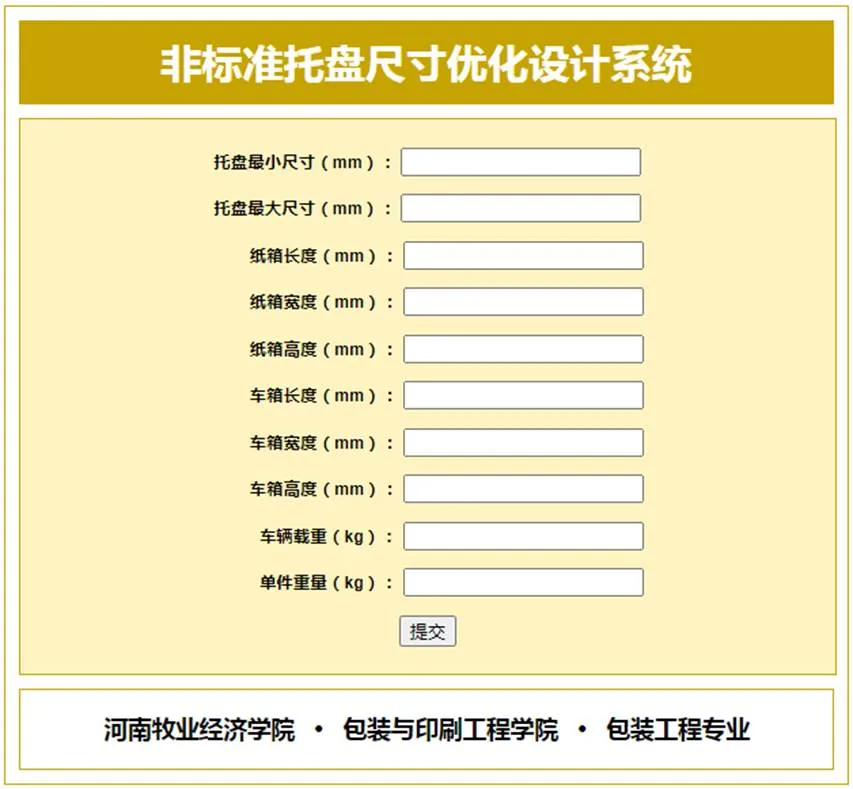
图8 产品信息输入界面

图9 优化结果输出界面

简单重叠式堆码模块、正反交错式堆码模块、旋转交错式堆码模块中点击查看托盘堆码方式部分见图10a、b、c。

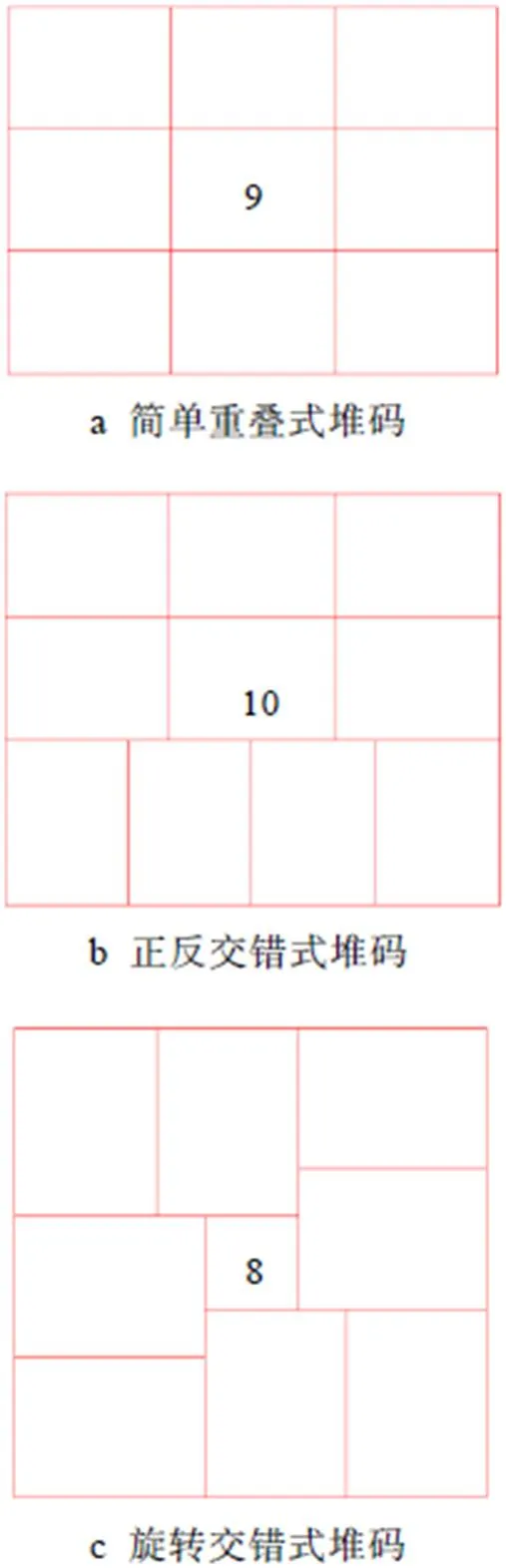
图10 不同堆码方式最优方案单层示意图

3.3 结果分析

同一堆码方式在编写程序时，按照num值最大作为最后显示数据。不同堆码方式的num值不同，选择num值最大的堆码方式所对应的托盘尺寸，且托盘尺寸接近标准尺寸。图9中，正反交错式堆码的车厢总排列数量为3 060，简单重叠式为3 078，旋转交错式为2 448，而且正反交错式堆码所对应的托盘尺寸为1 200 mm×1 029 mm，正反交错堆码数量稍小于简单重叠式，但其堆码稳定性要好于简单重叠式，所以从安全性和运输成本2个角度综合判断，选择正反交错式堆码的优化结果作为最优方案。

以上算例可以看出通过比较车厢总排列数量，以及托盘尺寸，可以选出最优的堆码方式，确定合适的托盘尺寸。

4 结语

文中使用托盘装载货物的平面利用率和装入运输工具的空间利用率进行双重约束，采用典型的4种堆码形式进行堆码，以单车装货量最高为优化目标，研究了非标准托盘尺寸的优化方法，并设计了优化设计系统，最后进行了算例验证。该系统可以大大减少非标准的设计周期，提高物流效率，具有一定的实用价值[14]。该系统还存在有不足之处：首先该系统仅以长方体形状物体为装载对象进行优化算法的设计，适用物体形状有限[15]；其次是仅以4种典型的装载方式进行优化，所适用的装载方式有限。因此还需要在此基础上，进一步扩展优化系统所适用的物体形状及其装载方式。

[1] 赵雪翔. 非标准托盘尺寸优化算法研究[D]. 南宁: 广西大学, 2015: 37-41.

ZHAO Xue-xiang. The Research on the Optimization Algorithm of Nonstandard Pallet Size[D]. Nanning: Guangxi University, 2015: 37-41.

[2] 唐书军. 集装单元化在铁路货运中的应用研究[D]. 南昌: 华东交通大学, 2017: 1-56.

TANG Shu-jun. Research on Container Unit Technology Based on Railway Logistics[D]. Nanchang: East China Jiaotong University, 2017: 1-56.

[3] 秦鉴. 铁路同类适盘货物装载方案优化研究[J]. 山东科学, 2016, 29(5): 103-110.

QIN Jian. Optimization of Railway Pallet-Suited Freight Loading Scheme[J]. Shandong Science, 2016, 29(5): 103-110.

[4] 李伟, 杨超宇, 孟祥瑞. 基于混合遗传算法的多品种货物装箱问题研究[J]. 包装与食品机械, 2020, 38(3): 51-56.

LI Wei, YANG Chao-yu, MENG Xiang-rui. Study on Multi-Variety Cargo Packing Problem Based on Hybrid Genetic Algorithm[J]. Packaging and Food Machinery, 2020, 38(3): 51-56.

[5] 王张峰, 张家应, 李宏伟, 等. 基于启发式算法的托盘货物优化装载方法设计[J]. 国防交通工程与技术, 2017, 15(2): 28-32.

WANG Zhang-feng, ZHANG Jia-ying, LI Hong-wei, et al. On the Heuristic-Algorithm-Method-Based Design of the Optimized Loading Method for Cargoes to Be Pallet-Transported[J]. Traffic Engineering and Technology for National Defence, 2017, 15(2): 28-32.

[6] 袁梦. 集装箱单箱混合装载优化问题研究[D]. 大连: 东北财经大学, 2018: 1-56.

YUAN Meng. Optimization of Single Container Mix-Loading Problem[D]. Dalian: Dongbei University of Finance and Economics, 2018: 1-56.

[7] 张长勇, 吴智博, 王艳芳. 基于K–means的航空行李快速装箱算法[J]. 包装与食品机械, 2019, 37(3): 38-42.

ZHANG Chang-yong, WU Zhi-bo, WANG Yan-fang. Fast Container Loading Algorithm for Airline Luggage Registration Based on K-Means Clustering[J]. Packaging and Food Machinery, 2019, 37(3): 38-42.

[8] 孟冲, 宋华文, 陈柏松. 基于0—1整数线性规划的军事空运装载优化算法[J]. 西南交通大学学报, 2011, 46(3): 500-505.

MENG Chong, SONG Hua-wen, CHEN Bai-song. Optimization Algorithm of Military Airlift Loading Based on 0-1 Integer Linear Programming[J]. Journal of Southwest Jiaotong University, 2011, 46(3): 500-505.

[9] 陈丙成, 李艳华. 基于启发式算法的单航空集装器的装箱优化设计[J]. 包装工程, 2020, 41(17): 244-251.

CHEN Bing-cheng, LI Yan-hua. Optimal Design of Packing for Single Unit Load Device Based on Heuristic Algorithm[J]. Packaging Engineering, 2020, 41(17): 244-251.

[10] 杨斌, 郑子龙, 吕品. 聚类优化后的多品种货物配载的容重比平衡法研究[J]. 科学技术与工程, 2014, 14(25): 140-145.

YANG Bin, ZHENG Zi-long, LYU Pin. The CubadgeWeight Balance Algorithm for the Loading of Multi-Category Good after the Optimized Clustering[J]. Science Technology and Engineering, 2014, 14(25): 140-145.

[11] 胡贵彦, 吕丽静. 运输车辆的三维装载问题建模及优化[J]. 物流技术, 2015, 34(11): 133-135.

HU Gui-yan, LYU Li-jing. Study on Modeling and Optimization of 3D Loading Problem of Transportation Vehicles[J]. Logistics Technology, 2015, 34(11): 133- 135.

[12] 刘阿宁, 闭应洲, 王仁民, 等. CVRP中二维装载问题的研究[J]. 广西师范学院学报(自然科学版), 2012, 29(1): 72-76.

LIU A-ning, BI Ying-zhou, WANG Ren-min, et al. The Two-Dimensional Loading Problem for CVRP[J]. Journal of Guangxi Teachers Education University (Natural Science Edition), 2012, 29(1): 72-76.

[13] 朱向, 向延平. 多车多件货物平衡装载优化研究[J]. 工业工程, 2020, 23(3): 123-131.

ZHU Xiang, XIANG Yan-ping. An Optimization of Multi-Freights Loading into Multi-Cars with Balancing Constraints[J]. Industrial Engineering Journal, 2020, 23(3): 123-131.

[14] 张点. 圆柱和立方体的托盘装载优化设计[D]. 西安: 西安电子科技大学, 2019: 1-86.

ZHANG Dian. Optimum Design of Cylindrical and Cubic Pallet Loading[D]. Xi'an: Xidian University, 2019: 1-86.

[15] 彭国勋. 物流运输包装设计[M]. 北京: 文化发展出版社, 2019: 320-330.

PENG Guo-xun. Logistics Transportation Packaging Design[M]. Beijing: Cultural Development Press, 2019: 320-330.

Development of Non-standard Pallet Size Optimization Design System

SONG Wei-sheng, Xue Yang

(Henan University of Animal Husbandry and Economy, Zhengzhou 450046, China)

The paper aims to develop a non-standard pallet size optimization design system to improve logistics efficiency and reduce logistics cost. The plane utilization rate of goods loaded on pallets and the space utilization rate of transportation vehicles are used for double constraints. The stacking is carried out in four ways: simple overlap, positive and negative interleaving, crisscross and rotation interleaving. The optimization algorithm is constructed with the highest loading volume of a single vehicle as the optimization objective. On this basis, the optimization design system is designed and verified by a numerical example. According to the calculation of the given premise data, the optimal pallet size is 1 200 mm×1 029 mm, and the corresponding loading mode is positive and negative interleaving. The system has a certain practical value, but there are still some problems, such as the shape of the objects to be stacked and the way of stacking, and there is room for further improvement.

non-standard; pallet size; optimization design

TB485.3；TS206

A

1001-3563(2022)11-0205-07

10.19554/j.cnki.1001-3563.2022.11.027

2021–08–06

河南牧业经济学院博士启动基金（2019HNUAHEDF021）

宋卫生（1980—），男，硕士，河南牧业经济学院副教授，主要研究方向为包装工程与仿真分析。

责任编辑：曾钰婵