基于Sherwood–Frost模型构建聚乙烯泡沫拉伸本构

张武杰，付志强，刘艳华，何争辉，刘昊喆

基于Sherwood–Frost模型构建聚乙烯泡沫拉伸本构

张武杰a,b，付志强a,b，刘艳华a,b，何争辉a,b，刘昊喆a,b

（天津科技大学 a.轻工科学与工程学院 b.包装创新设计实验室，天津 300222）

研究聚乙烯泡沫的拉伸力学性能，并构建聚乙烯泡沫的拉伸本构模型。利用万能材料试验机对不同密度的聚乙烯泡沫进行不同拉伸速率的单轴拉伸实验，得到聚乙烯泡沫的拉伸应力–应变曲线；在Sherwood–Frost唯象本构模型框架的基础上，构建将密度和应变耦合的密度项，以及将应变率、应变和密度耦合的应变率项的拉伸本构模型。聚乙烯泡沫在断裂前的拉伸力学特性为非线性弹性，表现出明显的应变率强化效应，现有的密度项和应变率项与实验数据的拟合精度较低，最大平均误差分别可达11.76%、7.90%。新构建的密度项和应变率项与实验数据拟合精度较好，最大平均误差分别为1.17%、1.92%。新构建的拉伸本构模型能够更精确地描述聚乙烯泡沫单轴拉伸的应力应变关系，为聚乙烯泡沫的综合力学性能的进一步研究提供参考。

聚乙烯泡沫；拉伸力学性能；Sherwood–Frost本构模型；应变率效应

聚乙烯泡沫是一种由低密度聚乙烯经非交联物理挤出发泡的聚合物泡沫，具有优良的缓冲性能，在易碎品、食品、电子电器的缓冲包装中得到了广泛应用[1]。对聚乙烯泡沫力学性能及本构关系的研究大多集中在单轴压缩力学性能[2-7]。聚乙烯泡沫作为缓冲包装在实际运输冲击跌落中除了受到压缩负载，还会受到拉伸、剪切等作用，因此研究聚乙烯泡沫的拉伸性能对复杂受载下聚乙烯泡沫包装的评价具有较大意义。

在对聚合物泡沫经验型本构关系的研究中，目前应用较广泛的是Sherwood–Frost唯象本构模型，Sherwood等[8]对聚氨酯泡沫单轴压缩性能研究时，在前人的基础上将密度和环境温度考虑进去，从而构建了包含密度、温度、应变率的唯象本构模型框架，该模型假定密度、温度、应变率和应变对应力的影响是可分离的函数。许多学者在Sherwood–Frost唯象本构模型框架下进行改进，以适用于不同的泡沫材料的力学特性。胡时胜等[9]在对不同密度的聚氨酯泡沫动态压缩本构关系的研究时对密度项进行了改进，提出一种幂指关系表示密度与应变耦合影响应力。李俊等[10]通过实验得到了不同密度的聚乙烯泡沫压缩时的应力应变特征，认为密度和应变耦合影响着应力，并提出一种指数关系描述其影响。雷鹏等[5]对Sherwood–Frost唯象本构模型中的应变率项进行了改进，采用了类似Johnson–Cook本构模型中热激活机制Seeger模型与反比例函数结合的模型描述发泡聚乙烯单轴压缩时的应变率效应。聚合物泡沫拉伸力学性能本构模型建立的研究目前较少，卢子兴等[11]通过实验对聚氨酯泡沫塑料的拉伸力学性能和失效原理进行的研究，并沿用Sherwood–Frost唯象压缩本构模型进行对其本构关系进行描述。马赛尔等[12]利用万能材料试验机对高密度聚乙烯的拉伸力学性能进行了研究，并进行了应变率相关本构模型的建立。饶聪超等[13]对高密度聚乙烯结构发泡塑料的拉伸力学及损伤特性进行了研究，并构建了小应变范围内弹塑性本构关系，但目前研究在建立拉伸本构时没有考虑到拉伸与压缩、发泡与未发泡聚合物力学特性的差异。Sherwood–Frost唯象本构模型是建立在聚合物泡沫压缩力学行为上的，而聚合物泡沫拉伸和压缩微观结构力学变形模式显著不同[14-15]，聚合物泡沫在压缩条件下建立的本构是否适用于描述拉伸力学特性还有待研究。

文中以3种密度的聚乙烯泡沫为研究对象，结合单轴拉伸试验，在Sherwood–Frost唯象本构模型框架的基础上，考虑密度与应变、应变率与应变及密度的耦合作用，从而构建包含新的密度项和应变率项的聚乙烯泡沫拉伸本构模型。

1 实验

1.1 材料及仪器

主要材料：密度分别为14.5、28.6、40.6 kg/m3的聚乙烯泡沫，采自天津中天塑料制品有限公司。

主要仪器：美国Instron 3369万能材料试验机，美国英斯特朗公司；ETH–408–40–CP–AR可程式恒温恒湿试验箱，巨贸仪器（北京）有限公司。

1.2 方法

1.2.1 样品试件制备

试样加工依据《GBT 6344—2008软质泡沫聚合物材料拉伸强度和断裂伸长率的测定》，试样标距为55 mm、宽度为13 mm、厚度为1 mm。试样取样方向垂直于气泡上升方向，见图1a。同时采用环氧树脂处理试样夹具夹持部位，以防止试样在实验时由于夹持损伤而在夹持处断裂，之后在温度为28 ℃、相对湿度65%预处理24 h。

1.2.2 实验过程

使用万能材料试验机，见图1b，分别以16.5、33、165、330、495 mm/min的恒定拉伸速度对3种密度的聚乙烯泡沫试样进行拉伸直至断裂，每个密度每个速率下实验重复3次，结果取平均值。试样应变率可以经推导表示为拉伸速率与试样标距的比值，即为0.005、0.01、0.05、0.1、0.15 s−1。

图1 试样和万能材料试验机

2 结果与分析

2.1 拉伸应力应变特性及密度效应

3种密度的聚乙烯泡沫在0.005 s−1的拉伸应变率下的应力–应变曲线见图2，力学特性表现为大应变，非线性弹性，没有明显的屈服点。随着密度的提高，聚乙烯泡沫的断裂应变有所提升。在0～0.4应变处，相同应变处28.6 kg/m3密度的聚乙烯泡沫拉伸应力高于14.5 kg/m3密度的聚乙烯泡沫拉伸应力，然而在0.4应变到断裂处28.6 kg/m3密度的聚乙烯泡沫拉伸应力低于14.5 kg/m3密度的聚乙烯泡沫拉伸应力，40.6 kg/m3密度的聚乙烯泡沫拉伸应力随着应变的增加始终高于28.6 kg/m3密度的聚乙烯泡沫拉伸应力，出现这种力学特征可能与聚乙烯泡沫的泡孔拉伸变形及基材的拉伸力学特征有关[14]。

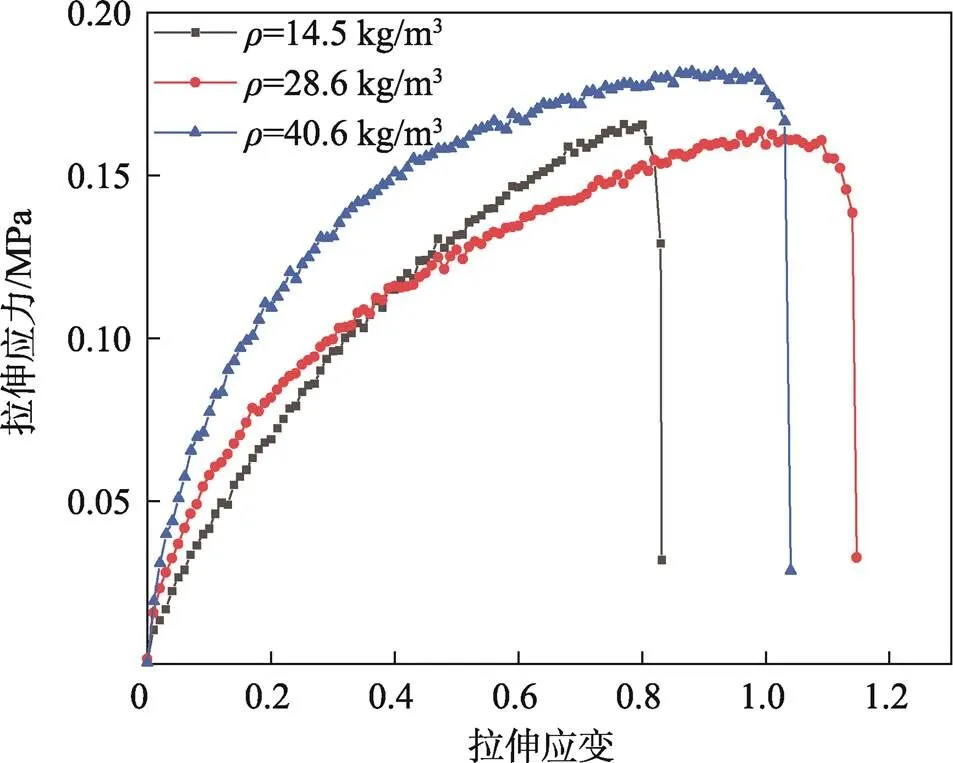
图2 3种密度的聚乙烯泡沫的拉伸应力–应变曲线

2.2 应变率效应

密度为14.5 kg/m3聚乙烯泡沫在不同应变率下的应力–应变曲线见图3，可以发现，在相同应变下，应力随应变率的增加随之增加，同聚乙烯泡沫压缩力学性能类似，拉伸力学性能也表现出应变率应力强化效应。

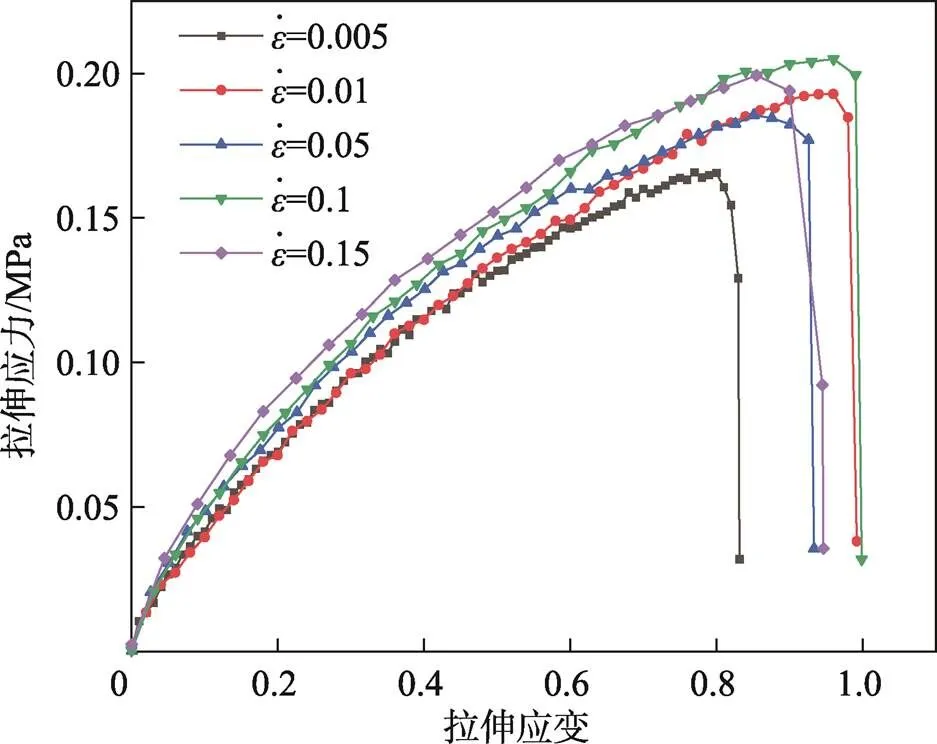
图3 密度为14.5 kg/m3的聚乙烯泡沫在不同应变率下的拉伸应力–应变曲线

3 本构模型的构建

3.1 Sherwood–Frost本构模型框架

Sherwood等[8]对聚氨酯泡沫单轴压缩性能研究时，在前人的基础上将密度和环境温度考虑进去，从而提出了比较全面的聚合物泡沫材料压缩本构关系框架，见式（1）。

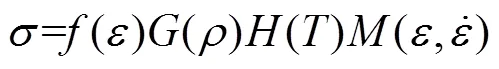
Sherwood–Frost模型采用了多项式描述应力–应变曲线并将其作为形状函数，此次研究依然采用多项式表示形状函数，见式（2）。选取聚乙烯泡沫拉伸断裂前0～0.8应变的应力应变曲线进行研究。

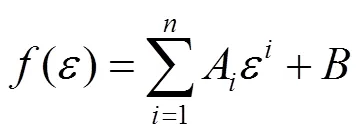
式中：A为形状函数拟合参数；为常量。

显然表达式中的参数越大，则拟合效果越好，但相应地也会增加计算的复杂性，文中选择=5。以14.5 kg/m3为参考密度，应变率为0.005 s−1拉伸应变率为参考值，选用多项式对实验数据进行拟合获得形状函数，见图4，拟合的形状函数参数见表1。

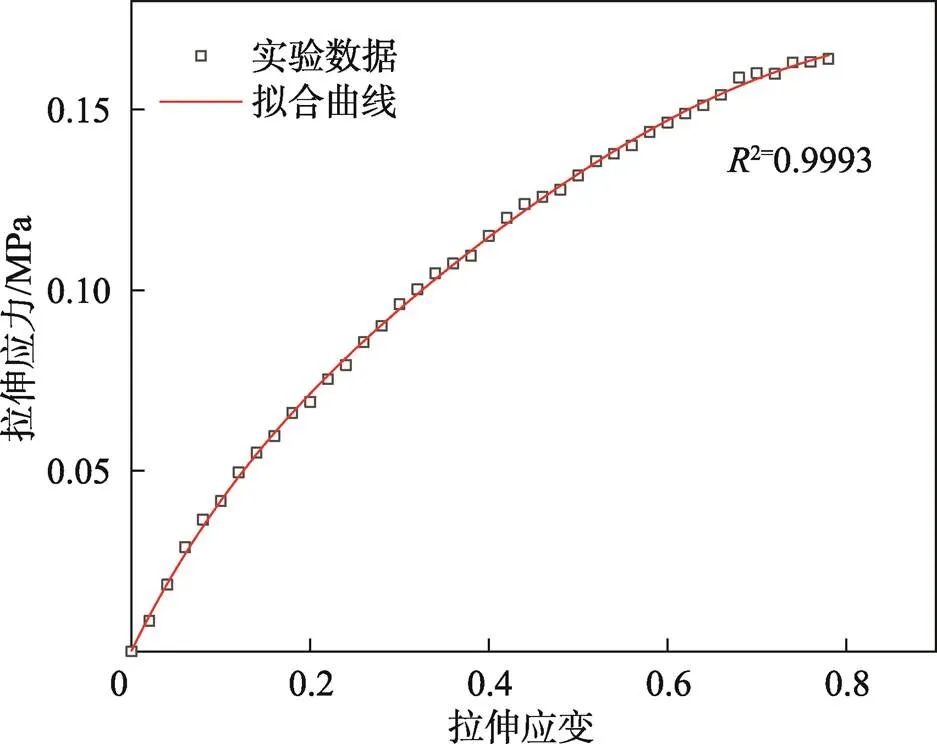
图4 形状函数拟合曲线与实验数据对比

表1 形状函数拟合参数

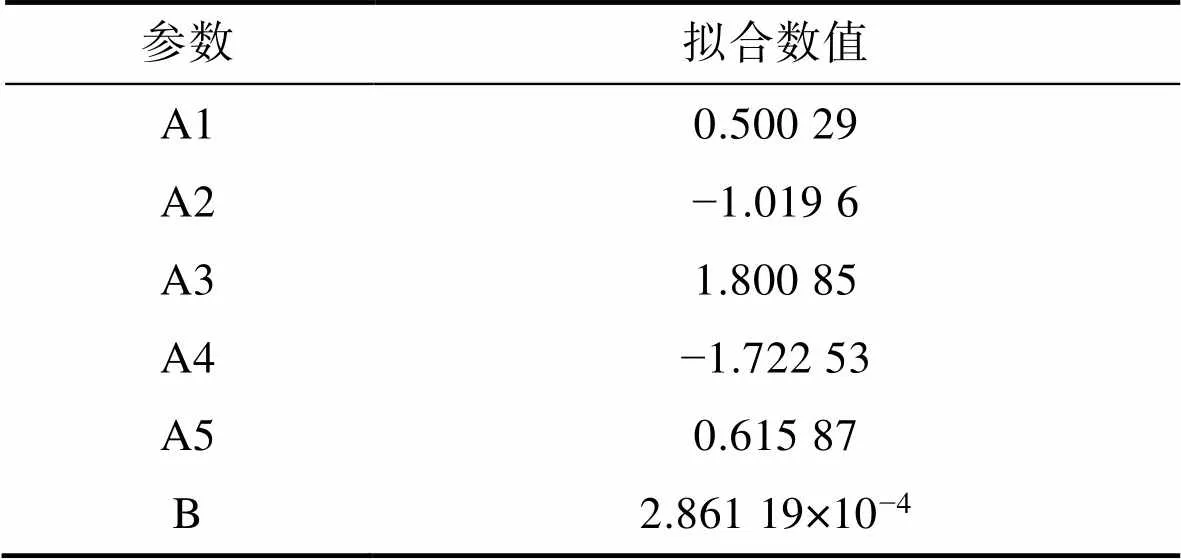
Tab.1 Fitting parameters of the shape function

3.2 密度项的改进及验证

Sherwood等认为密度对应力的影响是单一的，是与应变无关的。胡时胜等[9]在研究硬质聚氨酯泡沫塑料压缩力学性能时，发现密度对应力的影响程度还与所处的应变量有关，从而提出了一种应变和密度耦合的密度项，见式（3）。

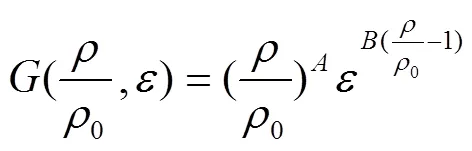
根据3种密度的聚乙烯泡沫的拉伸应力–应变数据可知，发现密度对拉伸应力的影响也与所处的拉伸应变有关，利用胡时胜等[9]提出的密度项对3种密度的聚乙烯泡沫在0.005 s−1应变率下的拉伸应力–应变曲线进行拟合。可以发现这种密度项拟合精度较低，没有很好地描述密度变化对聚乙烯泡沫材料拉伸力学性能的影响，同时参数的取值在不同密度时不同，这就导致了这种密度项不适合外推预测。为了更精确建立聚乙烯泡沫拉伸应力–应变特征随密度变化的关系，现重新推导密度项，不考虑应变率效应，Sherwood–Frost本构模型框架简化为式（4）。

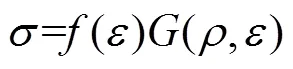
以最小密度14.5 kg/m3为参考密度，同一应变下应力与参考密度相同应变处的应力比值见式（5）。

通过实验数据可以发现不同应变下2组密度与参考密度的应力比值变化可以用改进后的弗伦德利希模型（Freundlich Model）函数来描述，见式（6），拟合效果见图5。参数与密度有关，又因实验材料密度只有3组，故列出不同密度下拟合参数的取值，见表2，密度和应变耦合后的密度项见式（6）。

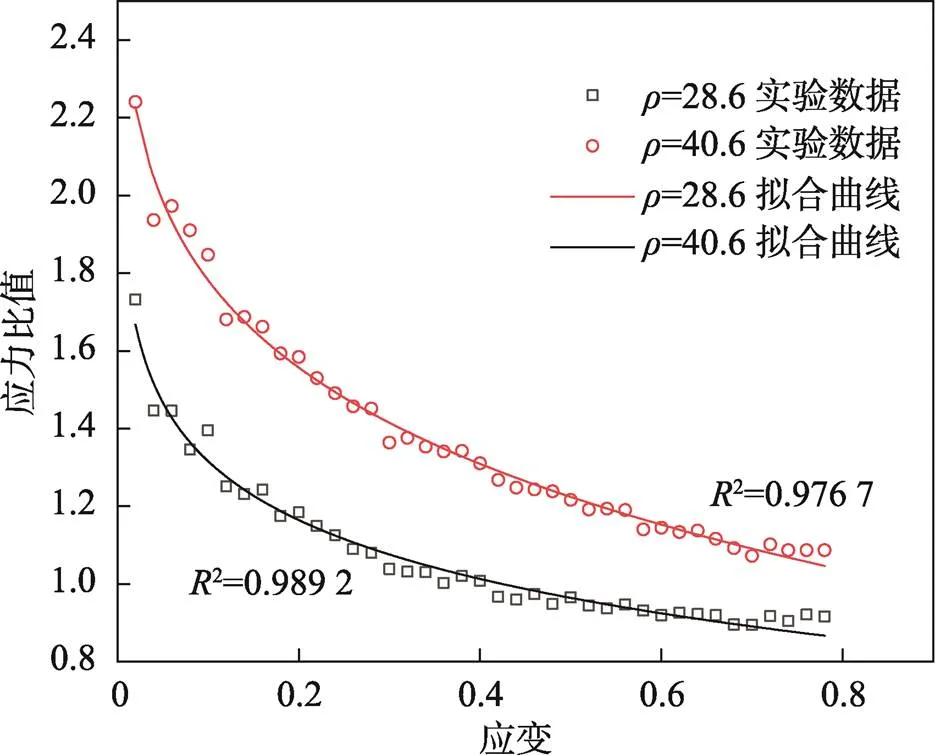
图5 不同密度下应力比值与应变的关系

表2 改进后的密度项的拟合参数

Tab.2 Fitting parameters of the improved density term

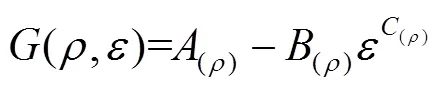
为了验证改进密度项后的本构模型的准确性和可靠性，将带入参数后的本构模型计算值与实验数据进行了对比验证，见图6。

误差计算见式（7）。

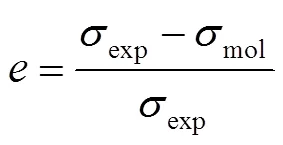
文中提出的耦合应变后的密度项与实验结果的拟合误差见表3，密度为28.6 kg/m3的平均误差为1.13%，密度为40.6 kg/m3的平均误差为1.17%，均小于现有密度项的误差值，新构建的密度项可以更精确地描述密度变化对聚乙烯泡沫材料拉伸力学性能影响。

3.3 应变率项的改进及验证

Sherwood等[8]在提出聚合物泡沫材料压缩本构关系时，应变率项采用了Nagy等[16]的研究成果，Nagy等在研究聚合物泡沫材料在动态压缩下的力学行为时，认为应变和应变率共同影响着应力，将应变率项构建为式（8）和式（9）。

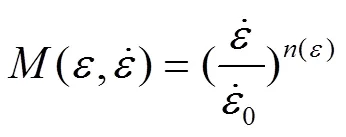
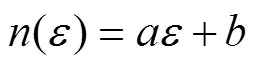
利用Nagy等[16]提出的应变率项对28.6 kg/m3的聚乙烯泡沫在不同应变率下的拉伸应力–应变曲线进行拟合，拟合结果见图9a。可以发现这种应变率项的拟合精度较低，没有很好地描述应变率变化对聚乙烯泡沫材料拉伸力学性能的影响。同时观察不同密度的聚乙烯泡沫在不同应变率下的拉伸应力–应变数据可知，应变率效应不仅与所处的应变量有关，还与密度有关，故对聚乙烯泡沫拉伸本构模型的应变率项进行推导，基于Sherwood–Frost本构模型框架，可将应变率项用式（10）表示。

对于最小密度14.5 kg/m3的聚乙烯泡沫，在0.3、0.5和0.7应变下，参考应变率与其他应变率下的应力比值与应变率比值的关系可以用幂函数来描述，见图7。通过origin软件使用最小二乘法拟合得到幂函数的参数n。

表3 密度项拟合误差

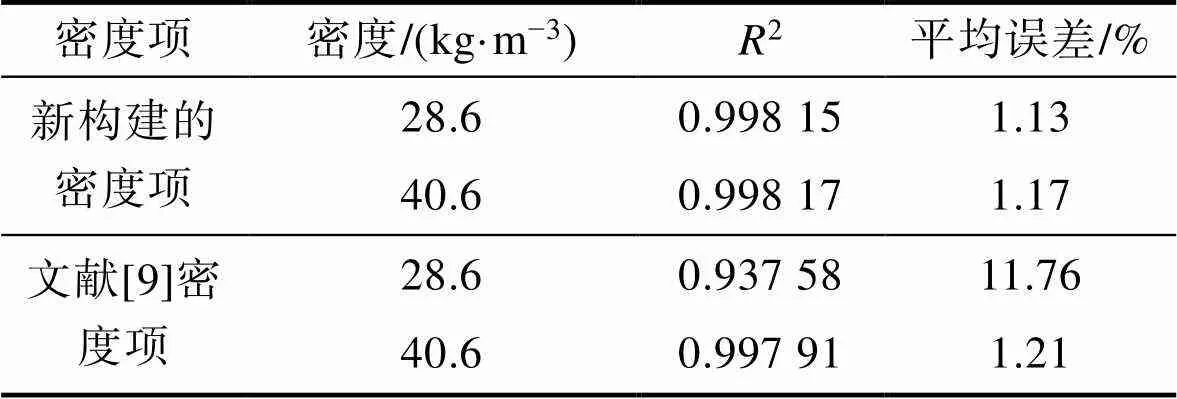
Tab.3 Fitting error of density term

图7 应变率比值与应力比值的关系及其拟合曲线

同时观察到幂函数的参数与应变和密度有关，见图8。根据参数随应变、密度的变化，选用Allometric幂函数描述这种变化趋势，见式（11），拟合参数见表4。

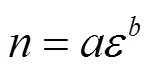
式中：、为与密度有关的拟合参数。

应变率、应变与密度耦合后构建的聚乙烯泡沫拉伸本构模型中的应变率项见式（12）和式（13）。

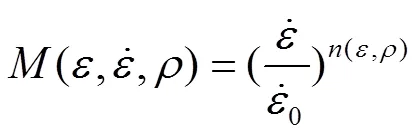
表4 参数与应变关系的拟合参数

Tab.4 Fitting parameter between parameter n and strain

为了验证改进应变率项后的本构模型的准确性和可靠性，将带入参数后的本构模型计算值与实验数据进行了对比验证，见图9b，本构模型的计算值与实验的误差见表5。

由图9和表5可知，28.6 kg/m3的聚乙烯泡沫在0.05 s−1应变率下的应力–应变实验数据与新构建的应变率项的计算结果的平均误差为1.44%，在0.15 s−1应变率下误差为1.92%，均小于现有的应变率项的误差值，可以更精确地描述聚乙烯泡沫在不同应变率下的拉伸应力–应变关系。

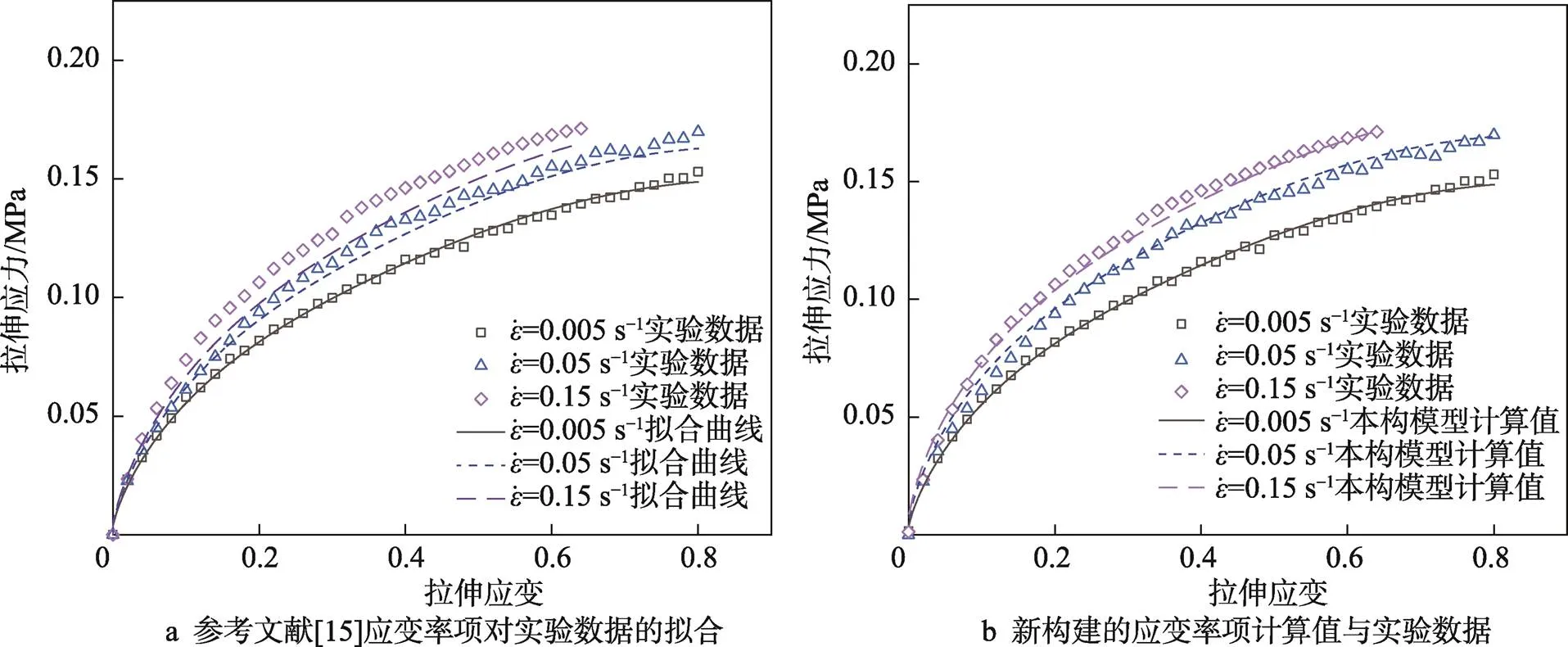
图9 28.6 kg/m3的聚乙烯泡沫在不同应变率下的应力–应变曲线实验数据与本构模型计算值

表5 密度为28.6 kg/m3的聚乙烯泡沫的本构模型计算值与实验数据的误差

Tab.5 The error between the calculated value of the constitutive model of the polyethylene foam of 28.6 kg/m3 and the experimental data

综上所述，聚乙烯泡沫拉伸本构模型见式（14）—（15）。

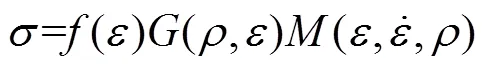
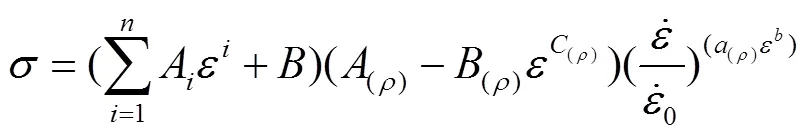
4 结语

文中通过拉伸实验发现聚乙烯泡沫单轴拉伸力学性能表现为非线性弹性，没有明显的屈服点，在断裂前可以达到0.8以上的大应变，并且表现出密度及应变率强化效应。经典的Sherwood–Frost本构模型假定密度、温度、应变和应变率对应力的影响是可分离的函数，而基于Sherwood–Frost模型直接描述聚乙烯泡沫拉伸本构关系时误差较大，在Sherwood–Frost本构模型框架的基础上结合实验数据规律构建了密度和应变耦合的密度项以及应变率和密度、应变耦合的应变率项，耦合后的本构模型与实验数据误差较小，可以更精确地描述聚乙烯泡沫拉伸应力–应变关系。聚乙烯泡沫拉伸性能的研究及本构模型的构建可以为聚乙烯泡沫的综合力学性能的研究提供一定的参考和依据。

[1] 郭鹏, 徐耀辉, 张师军, 等. 聚乙烯发泡材料的研究进展[J]. 石油化工, 2015, 44(2): 261-266.

GUO Peng, XU Yao-hui, ZHANG Shi-jun, et al. Progresses in Research of Polyethylene Foaming Materials[J]. Petrochemical Technology, 2015, 44(2): 261-266.

[2] YANG B, ZUO Y, CHANG Z. Evaluation of Energy Absorption Capabilities of Polyethylene Foam under Impact Deformation[J]. Materials (Basel, Switzerland), 2021, 14(13): 3613.

[3] LU Fu-de, HUA Guang-jun, WANG Li-shu, et al. A Phenomenological Constitutive Modelling of Polyethylene Foam under Multiple Impact Conditions[J]. Packaging Technology and Science, 2019, 32(7): 367-379.

[4] 徐绍虎, 崔爽. 基于本构模型的发泡聚乙烯缓冲特性曲线研究[J]. 包装工程, 2019, 40(15): 11-15.

XU Shao-hu, CUI Shuang. Expanded Polyethylene Cushion Curve Based on Constitutive Model[J]. Packaging Engineering, 2019, 40(15): 11-15.

[5] 雷鹏, 付志强, 张蕾, 等. 基于改进后Sherwood– Frost本构模型对EPE冲击模拟[J]. 包装工程, 2019, 40(7): 32-37.

LEI Peng, FU Zhi-qiang, ZHANG Lei, et al. EPE Impact Simulation Based on Improved Sherwood–Frost Constitutive Model[J]. Packaging Engineering, 2019, 40(7): 32-37.

[6] 韦青, 郭彦峰, 付云岗, 等. 聚乙烯泡沫单填充纸蜂窝夹层管的轴向缓冲吸能特性[J]. 机械工程学报, 2021, 57(2): 112-120.

WEI Qing, GUO Yan-feng, FU Yun-gang, et al. Cushioning Energy Absorption of Paper Honeycomb Sandwich Tube Single-Filled by Polyethylene Foam under Axial Drop Impact[J]. Journal of Mechanical Engineering, 2021, 57(2): 112-120.

[7] JOODAKY A, BATT G S, GIBERT J M. Prediction of Cushion Curves of Polymer Foams Using a Nonlinear Distributed Parameter Model[J]. Packaging Technology and Science, 2020, 33(1): 3-14.

[8] SHERWOOD J A, FROST C C. Constitutive Modeling and Simulation of Energy Absorbing Polyurethane Foam under Impact Loading[J]. Polymer Engineering & Science, 1992, 32(16): 1138-1146.

[9] 胡时胜, 刘剑飞, 王梧. 硬质聚氨酯泡沫塑料本构关系的研究[J]. 力学学报, 1998, 30(2): 151-156.

HU Shi-sheng, LIU Jian-fei, WANG Wu. Study of the Constitutive Relationship of Rigid Polyurethane Foam [J]. Acta Mechanica Sinica, 1998, 30(2): 151-156.

[10] 李俊, 高德, 王振林. 低密度聚乙烯泡沫塑料压缩本构关系的研究[J]. 包装工程, 2008, 29(12): 25-26.

LI Jun, GAO De, WANG Zhen-lin. Study of the Constitutive Relation of Low Density Plyethylene Foam under Compression[J]. Packaging Engineering, 2008, 29(12): 25-26.

[11] 卢子兴. 聚氨酯泡沫塑料拉伸本构关系及其失效机理的研究[J]. 航空学报, 2002, 23(2): 151-154.

LU Zi-xing. Investigation into the Tensile Constitutive Relation and Failure Mechanism of Pur Foamed Plastics[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(2): 151-154.

[12] 马赛尔, 许进升, 童心, 等. 高密度聚乙烯单轴拉伸力学性能及本构关系研究[J]. 中国塑料, 2016, 30(4): 88-92.

MA Sai-er, XU Jin-sheng, TONG Xin, et al. Research on Uniaxially Tensile Mechanical Properties and Constitutive Model of High Density Polyethylene[J]. China Plastics, 2016, 30(4): 88-92.

[13] 饶聪超, 姜献峰, 李俊源, 等. 高密度聚乙烯结构发泡塑料拉伸本构关系的研究[J]. 中国塑料, 2012, 26(7): 66-69.

RAO Cong-chao, JIANG Xian-feng, LI Jun-yuan, et al. Research on Constitutive Relation of High-Density Polyethylene Structural Foam under Tensile[J]. China Plastics, 2012, 26(7): 66-69.

[14] GIBSON L J, ASHBY M F. Cellular Solids: Structure and Properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997: 234-236.

[15] CHEN Wen-su, HAO Hong, HUGHES D, et al. Static and Dynamic Mechanical Properties of Expanded Polystyrene[J]. Materials & Design, 2015, 69: 170-180.

[16] NAGY A. Mechanical Behavior of Foamed Materials under Dynamic Compression[J]. Journal of Cellular Plastics, 1974, 10(3): 127-134.

Construction of Constitutive of Polyethylene Foam Under Tensile Based on Sherwood-Frost Model

ZHANG Wu-jiea,b, FU Zhi-qianga,b, LIU Yan-huaa,b, HE Zheng-huia,b, LIU Hao-zhea,b

(a. School of Light Industry Science and Engineering b. Laboratory for Innovative Design of Package, Tianjin University of Science & Technology, Tianjin 300222, China)

The project aims to study the tensile mechanical properties of polyethylene foam and construct its constitutive model under tensile. The universal material testing machine is used to perform uniaxial tensile tests on polyethylene foams of different densities at different tensile rates, and the tensile stress-strain curves of the polyethylene foams are obtained; Based on the Sherwood-Frost phenomenological constitutive model frame, a tensile constitutive model of the density term coupling density and strain and the strain rate term coupling strain rate, strain and density are constructed. The tensile properties of polyethylene foam before fracture are nonlinear elasticity, showing obvious strain rate correlation. The existing density term and strain rate term have low fitting accuracy with experimental data, and the maximum average error can reach 11.76% and 7.90% respectively. The newly constructed density term and strain rate term have better fitting accuracy with the experimental data, and the maximum average error is 1.17% and 1.92% respectively. The constructed tensile constitutive model can more accurately describe the stress-strain relationship of polyethylene foam under uniaxially tensile, and provide a reference for further research on the mechanical properties of polyethylene foam.

polyethylene foam; tensile mechanical properties; Sherwood-Frost constitutive model; strain rate effect

TB484.3

A

1001-3563(2022)11-0161-07

10.19554/j.cnki.1001-3563.2022.11.021

2021–09–13

天津市教委科研计划（2019KJ209）

张武杰（1996—），男，天津科技大学硕士生，主攻包装动力学。

付志强（1982—），男，博士，天津科技大学讲师，主要研究方向为运输包装数值模拟技术。

责任编辑：曾钰婵