基于可变轴距拖拉机平台悬挂式农具的撒肥机研制*
2022-06-20高巧明许鹏王连其黄贵东唐能宁业烈
高巧明,许鹏,王连其,黄贵东, ,唐能,宁业烈
(1. 广西科技大学机械与交通工程学院,广西柳州,545006;2. 广西合浦县惠来宝机械制造有限公司,广西北海,536100;3. 柳州博实唯汽车科技股份有限公司,广西柳州,545006)
0 引言
我国高原和丘陵山地面积6.66亿hm2,占国土总面积的69.4%,丘陵山地农机化率长期低于平原地区,由于路窄弯多、作物多样等因素,常常面临无机可用的局面[1]。丘陵山地地区的农业机械化水平在播撒环节与全国其他地区差距有扩大趋势,且目前我国有机肥应用率为20%,远低于国外发达国家。
在产品研制上,国外针对撒肥机的机械性能研究比较多[2-4]。法国的MDS、AGT、UKS系列、美国的NC系列、德国的ZA系列、英国的HL、TL系列的撒肥机结构复杂、技术先进导致国内用户进口成本较高;国内因受不同地区地貌特征影响,有机肥单位面积撒施量较大,人工撒布耗时费工,且有机肥存在复杂物理特性,国内市场目前仍缺乏相对成熟稳定、系列化的撒肥机[5]。目前已开展适合我国国情的代表性研究成果主要有:吕金庆等[6-8]设计了一种锥盘式撒肥装置,建立了肥料颗粒的运动模型分析锥形撒肥圆盘结构和运动参数对抛撒的影响,施印炎等[9]基于近地光谱技术设计了一种基于传感器的双圆盘离心匀肥罩式水稻地表变量施肥机;胡永光等[10]基于离散元的撒肥过程仿真设计了叶片位置倾角可调的偏置式撒肥离心盘;芦新春等人针对施肥均匀性稳定性设计了一种同轴驱动的离心式双圆盘撒肥机;张睿等[11]应用变量施肥技术设计了一种基于处方图的链条输送式变量施肥抛撒机;陈书法等[12]研究设计了水田高地隙专用底盘、撒肥盘及排肥口调节装置;但目前针对有机肥的抛撒均匀性和定量施肥的研究仍相对较少。
利用山地铰接轮式可变轴距拖拉机作为平台悬挂机具的搭建平台,成功研制了平台悬挂式撒肥机,并通过田间试验,选择合理的行走速度、撒肥机圆盘转速、排料口处手柄调节高度等参数。
1 平台悬挂式撒肥机技术参数与工作原理
1.1 平台悬挂式撒肥机技术参数
设计的平台悬挂式撒肥机如图1所示,主要由牵引架、肥料箱、排料口处手柄调节机构、车架焊合、撒肥盘总成、送肥装置等部件组成;整机主要的技术指标参数如表1所示。

图1 整机结构

表1 主要设计参数Tab. 1 Primary technical parameters
1.2 撒肥机工作原理
如图1所示,通过拖拉机液压系统驱动液压马达工作,通过驱动输肥装置链板将肥料向后输入,同时PTO传动轴驱动齿轮箱带动离心式撒肥盘高速转动,排料口处设置手柄调节机构,用户可根据所需施肥量自行调节控制下落的肥料量,并使肥料在重力作用下落到撒肥圆盘上,通过撒肥盘总成上的圆盘离心作用和推肥叶片的导向作用实现肥料在空中做斜抛运动实现肥料宽幅、均匀稳定的抛撒作业要求。
2 平台悬挂式撒肥机结构设计
2.1 播撒装置结构设计
撒肥盘结构设计是决定厩肥抛撒幅宽及抛撒均匀性的重要因素,也是撒肥机满足在丘陵山地地区宽幅高效撒肥作业要求的重要保证[13]。如图2所示,撒肥盘主要由撒肥圆盘和3个推肥叶片组成,且已有研究表明叶片长度、圆盘转速、肥料颗粒自旋运动、撒肥高度、圆盘叶片位置角、肥料下落位置角对其抛撒均匀性及抛撒幅宽有重要影响[14-15]。设计的撒肥圆盘直径D为520 mm,撒肥圆盘结构采用倾角3°~5°的倒锥形,以减少肥料颗粒在撒肥圆盘上的弹落损失。

图2 撒肥盘结构
撒肥盘的材料采用Q235钢板,厚度为3 mm,撒肥盘内肥料为10 kg,要求转速为700 r/min,撒肥盘5 s内达到额定转速。
撒肥盘的质量
m转=πR12hρ
式中:R1——撒肥盘半径,m;
h——撒肥盘厚度,m;
ρ——钢板的密度,kg/m。
角加速度
m总=m转+m肥=14.96 kg
式中:ω——撒肥盘的角速度,rad/s;
t——时间,s;
n——撒肥盘的转速,r/min;
m肥——肥料质量,kg;
m总——撒肥盘的总质量,kg。
转动惯量
转动扭矩
2.2 输肥装置结构设计
输肥装置结构设计决定了肥料输送的稳定性,间接决定撒肥机的抛撒性能。为了保证肥料稳定、均匀的输送,本文设计采取结构简单、输送能力大、运行平稳的刮板式输送装置,如图3所示,主要由主动链轮轴总成、刮肥板总成、矿用圆环链、从动链轮轴总成组成;主动链轮带动刮肥板运动,进而给肥料箱中肥料反作用力用来克服与肥料箱的滑动摩擦力从而将肥料输送给撒肥圆盘上进行抛撒作业。

图3 输肥装置结构
2.3 撒肥机液压系统设计
液压系统控制结构原理如图4所示。
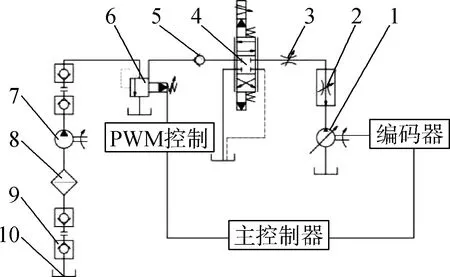
图4 液压系统图
系统采用拖拉机的液压油箱,通过进油节流调速回路,使液压马达转速通过PWM电路控制流量达到调速目的,同时通过编码器进行液压马达转速反馈,同时使用快速接头可通过简单动作实现拆断和连接油路时,快速接头上的单向阀封闭油路避免油液流出而造成油压损失,同时也节省时间和人力。液压泵最大工作压力
Ppmax≥P1max+∑ΔP
式中:P1max——液压执行元件最大工作压力;
∑ΔP——从液压泵出口到执行元件入口之间的压力损失总和。
已知液压马达的型号为BMP-100,其额定压力为17.5 MPa,液压泵出口到执行元件入口之间的压力损失总和∑ΔP按设计手册初选为0.5 MPa,带入计算得出液压泵最大工作压力Ppmax≥18 MPa。因为在选取液压泵过程中,需要使液压泵有一定的压力储备。一般额定工作压力比最大工作压力高20%~60%。所以液压泵的额定压力为21.60~28.80 MPa。
液压泵的流量
qp≥K(∑q)max
式中:K——考虑系统泄露和溢流阀保持最小溢流量的系数。一般取值为1.1~1.3之间,现取K=1.2;
(∑q)max——同时工作的执行元件的最大总流量;
计算得出qp≥93.6 L/min
驱动功率
式中:ηp——液压泵的总效率,一般取ηp=0.8。
驱动功率Pp=21.06 kW,由表1可知,牵引装置的额定功率为36.8 kW,满足驱动条件。
3 肥料运动特性分析
肥料从撒肥盘中脱离时,同时受到空气阻力和重力等多重作用,在空气中作斜抛运动,运动轨迹如图5所示。肥料脱离撒肥盘的必要条件为:滑动摩擦的阻力小于撒肥盘的离心力,即满足公式
f摩=umg
f离=mrω2
式中:u——肥料与圆盘表面摩擦系数;
m——肥料颗粒质量;
g——重力加速度;
r——肥料颗粒落在圆盘到圆盘中心的距离。

图5 肥料抛撒运动学分析示意图
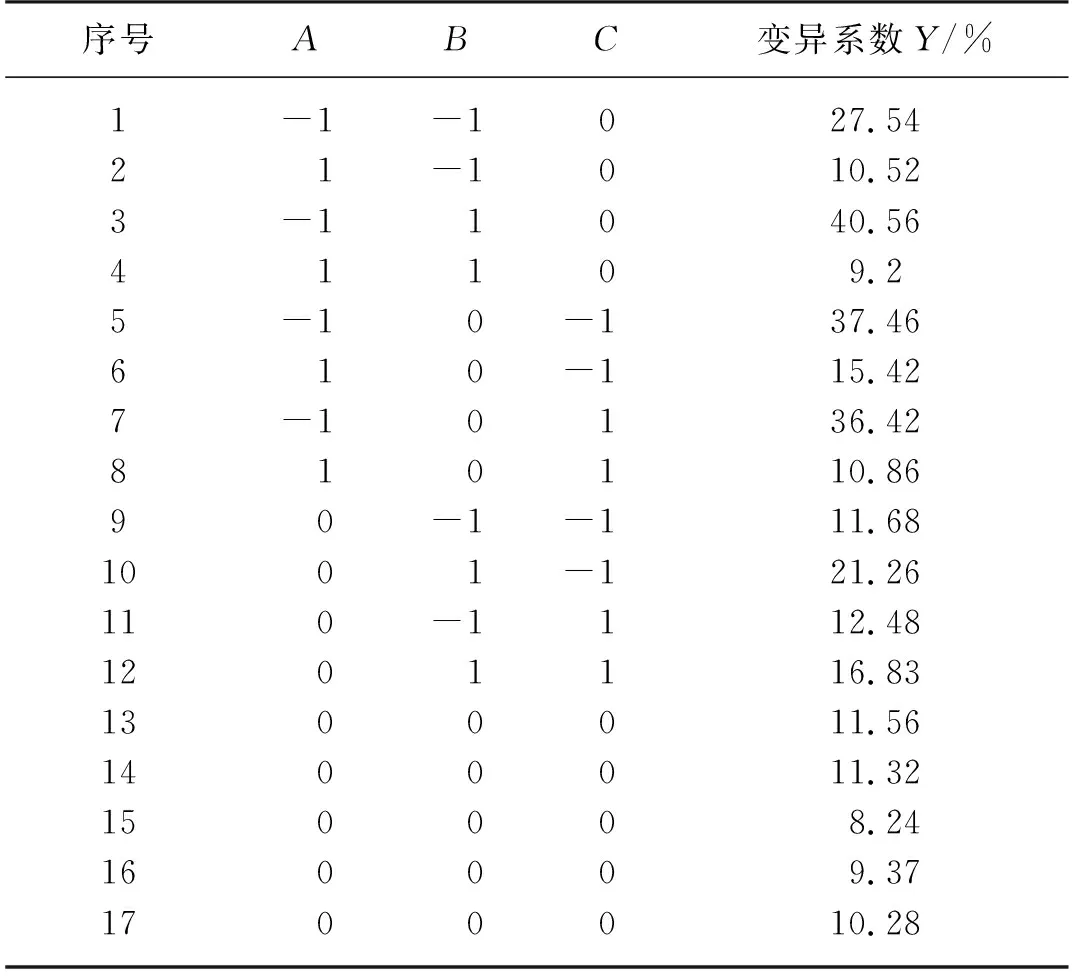
当f摩 此时圆盘角速度和最低转速 肥料刚离开圆盘的速度 v=2πnr 肥料离心抛出任意时刻t内速度方程 vx=vcosθ vy=vsinθ-gt 且 肥料抛撒落地位移 S=Vx(t1+t2) 由于抛撒机构与连接座相连接的转轴转速恒定,忽略肥料自身运动和空气阻力影响时,抛撒落地点距离只与入射角θ有关,当θ=π/4时,抛撒距离最远。 有机肥主要由农业秸秆、畜禽粪便、各种饼肥等组成,撒肥圆盘和车架选用45号钢,通过查阅相关文献[16]得出材料的各个参数如表2所示。 表2 主要设计参数Tab. 2 Material parameters 有机肥与撒肥圆盘之间选用Herta-MinDlin (No slip)接触模型。在分析过程中,有机肥和撒肥盘之间为弹性接触,假设Ri,Rj分别是两个肥料颗粒的半径,δn为两肥料颗粒之间的法相重叠量,肥料颗粒间所受到的法向接触力 其中,E*和R*分别为等效弹性模量和等效直径,其计算公式分别为 式中:Ei——肥料颗粒i的弹性模量; Ej——肥料颗粒j的弹性模量; vi——肥料颗粒i的泊松比; vj——肥料颗粒j的泊松比。 有机肥之间选用Herta-MinDlin with JKR cohesion 接触模型。JKR法向力基于重叠量δ和相互作用参数、表面能量γ 查阅相关文献[16]得,各接触参数如表3所示。 表3 材料基本接触参数Tab. 3 Material basic contact parameters 有机肥颗粒选用三球面颗粒来模拟,颗粒如图6所示,大小分布如表4所示。 图6 肥料颗粒模型 表4 颗粒大小占比Tab. 4 Percentage of particle size 最小单个有机肥颗粒质量为0.003 16 kg。撒肥盘转速为700 r/min,撒肥机作业速度为0.8 m/s,时间步设置为20%,仿真时间为3.5 s,需要迭代2.37×105次,每0.01 s存储一次数据。 撒肥机在作业过程中,每一个有机肥的运动轨迹、受力情况以及速度变化情况不尽相同,如图7所示,在EDEM中将其运动轨迹进行可视化处理。并将其数据导出,分别对肥料受力以及速度变化的规律进行分析,为进一步研究提供依据。 图7 有机肥颗粒运动轨迹 4.2.1 有机肥颗粒受力情况分析 由图8可以看出,在0.9 s之前,由于有机肥在颗粒工厂中还未生成,所以受到的合力为0;在0.9~1 s期间,有机肥由颗粒工厂中落下,到达撒肥盘,此时受到的力约为4×10-4N;1~2.9 s之间,此时有机肥颗粒较多,伴随着撒肥圆盘的转动,有机肥颗粒之间会产生一定的相互作用,此时有机肥受到的力是多种因素的合力,因此,这段期间颗粒的受力波动性较大,其中,在1.1 s时达到顶峰,为8.8×10-4N,在2.9 s之后,有机肥颗粒受到撒肥盘的离心力作用,抛到地面,完成施肥作业。 图8 力随时间变化曲线 4.2.2 有机肥颗粒速度变化情况分析 图9为颗粒速度随时间变化曲线,由图9可知,肥料颗粒在1 s生成,受到重力的作用而呈自由落体运动,1.2~3 s之间有机肥颗粒在撒肥盘上做无规则运动,此时肥料的速度一直是波动状态,其中,在1.5 s时,肥料运动的速度达到最大值,为6.49 m/s,在3 s过后,此时施肥已经完成作业,肥料颗粒落地,但由于撒肥机仍匀速向前运动,所以,此时的有机肥颗粒相对于撒肥机仍然是0.8 m/s。 图9 速度随时间变化曲线 通过调研优化国内外已有撒肥机的成熟技术生产工艺,在天气晴朗,温度和空气湿度适宜,微风的环境下,试验方法根据文献[17-19],选择肥料为厩肥,试验场地选择在广西合浦县惠来宝机械制造有限公司的平整无明显坡度路面进行撒肥性能检测,选择试验场地为8 m×10 m矩形区域,为了便于收集肥料,在试验区域事先铺好塑料布,试验采用定点收集的方法对抛撒装置抛出的肥料进行收集,在抛撒装置宽幅稳定运行范围内摆放30个形成6×5的收集矩阵,其中列间隔1.5 m,行间隔1 m,按从左到右,从下到上编号0~30,撒肥机以一定的作业速度从纵向对称中心穿过后,收集盒摆放如图10所示。Y轴为撒肥机的中轴线,正方向为撒肥机的行驶方向。试验以横向撒肥变异系数为评价指标,其计算公式 式中:CV——均匀度变异系数; s——标准差; k——收集盒的列数; xi——i列收集盒中肥料的质量之和,kg。 试验选取撒肥机行走速度、撒肥机圆盘转速、排料口处手柄调节高度3个因素设计三元二次回归正交旋转组合试验,试验因素编码如表5所示,试验设计与结果如表6所示,表6中A、B、C分别为3个因素编码,变异系数为Y,每组试验完成后,对每个框中的肥料进行装袋称量,记录数据并计算肥料分布变异系数填入表6中。 图10 撒肥示意图 表5 因素水平编码Tab. 5 Factor level coding 表6 试验设计与结果Tab. 6 Experimental design and results 采用Design-Expert 8.0.6软件对表6中结果进行回归分析得到的变异系数二次多项式模型的方差分析如表7所示,调整R2为0.989表明回归模型与试验值符合程度较好,依据系数间不存在线性相关性,经逐步回归法剔除不显著因素得到变异系数Y与撒肥机行走速度A、撒肥机圆盘转速B、排料口处手柄调节高度C的二次回归方程 Y=10.15-12.00A+3.20B-1.15C-3.59AB+0.88AC-1.31BC+10.64A2+1.16B2+4.25C2 由方程中系数绝对值大小决定该因素对分布变异系数的影响可知,各因素对试验指标影响的显著性由大到小依次为撒肥机行走速度、撒肥机圆盘转速、排料口处手柄调节高度。 表7 变异系数二次多项式模型的方差分析Tab. 7 Analysis of variance of the quadratic polynomialmodel of coefficient of variation 为直观地分析试验指标撒肥变异系数和3个因素之间的关系,利用 Design-Expert 8.0.6 软件绘制交互作用显著因素间的3D响应曲面,如图11所示,得到以分布变异系数最小为原则,撒肥机行走速度在0.6 m/s, 撒肥机圆盘转速在700 r/min,排料口处手柄调节高度在40 mm时变异系数最小为8.24%。而双因素交互作用对分布变异系数的影响主要有以下3点。 1) 由图11(a)可知,撒肥机行走速度对分布变异系数的影响比撒肥机圆盘转速大,分布变异系数随着撒肥机行走速度和撒肥机圆盘转速的增加均呈现出先快速减小后缓慢增大的趋势;在撒肥机行走速度在0.7~0.9 m/s,撒肥机圆盘转速在600~700 r/min范围内,分布变异系数较小。 2) 由图11(b)可知,撒肥机行走速度对分布变异系数的影响比排料口处手柄调节高度大,分布变异系数随着撒肥机行走速度和排料口处手柄调节高度的增加均呈现出先快速减小后缓慢增大的趋势;在撒肥机行走速度在0.7~0.9 m/s, 排料口处手柄调节高度在36~44 mm范围内,分布变异系数较小。 3) 由图11(c)可知,撒肥机圆盘转速对分布变异系数的影响比排料口处手柄调节高度大,分布变异系数随着撒肥机圆盘转速增加呈现出增大的趋势;随着排料口处手柄调节高度的增加呈现出先减小后增大的趋势;撒肥机圆盘转速在700~750 r/min范围内,排料口处手柄调节高度在36~44 mm范围内,分布变异系数较小。 (a) 撒肥机行走速度A与撒肥机圆盘转速B交互作用 (b) 撒肥机行走速度A与排料口处手柄调节高度C交互作用 (c) 撒肥机圆盘转速B与排料口处手柄调节高度C交互作用 1) 利用山地铰接轮式可变轴距拖拉机作为平台悬挂机具的搭建平台,研制了平台悬挂式撒肥机。实现了丘陵山地地区宽幅高效、均匀稳定的撒肥作业要求,降低了生产成本并提高了农机化率。 2) 对撒肥机的播撒装置、输肥装置及液压系统进行设计。通过计算得出撒肥盘的转动扭矩为7.42 N·m,液压泵最大工作压力为18 MPa,液压泵流量为93.6 L/min,进一步得出驱动功率为21.06 kW。 3) 通过对抛撒肥料运动特性分析以及利用EDEM软件对有机肥颗粒的离心撒肥过程进行分析,得出有机肥颗粒在1.1 s时受力达到顶峰,为8.8×10-4N;在1.5 s时,运动的速度达到最大值,为6.49 m/s。 4) 通过多元回归正交旋转试验二次回归方程与响应面分析表明,各因素对试验指标撒肥均匀分布变异系数影响的显著性由大到小依次为撒肥机行走速度、撒肥机圆盘转速、排料口处手柄调节高度;且撒肥机行走速度与撒肥机圆盘转速交互作用、撒肥机行走速度与排料口处手柄调节高度时对分布变异系数的影响较为明显。 5) 利用 Design-Expert 8.0.6 软件绘制交互作用显著因素间的3D响应曲面,得到以分布变异系数最小为原则,撒肥机行走速度在0.6 m/s, 撒肥机圆盘转速在700 r/min,排料口处手柄调节高度在40 mm时变异系数最小为8.24%。4 离心撒肥过程仿真分析
4.1 仿真参数设置




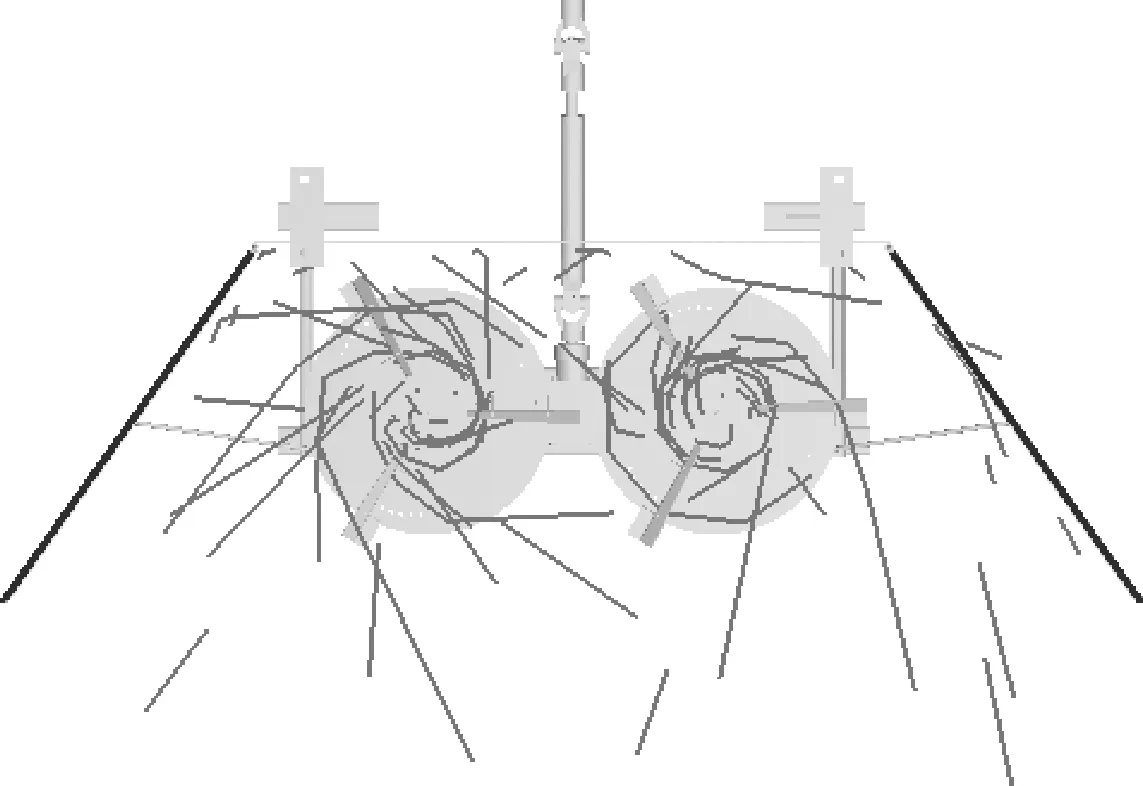
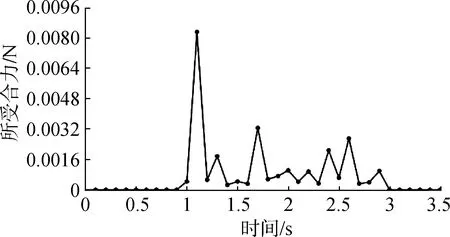
4.2 仿真结果分析

5 田间试验
5.1 样机试制与试验


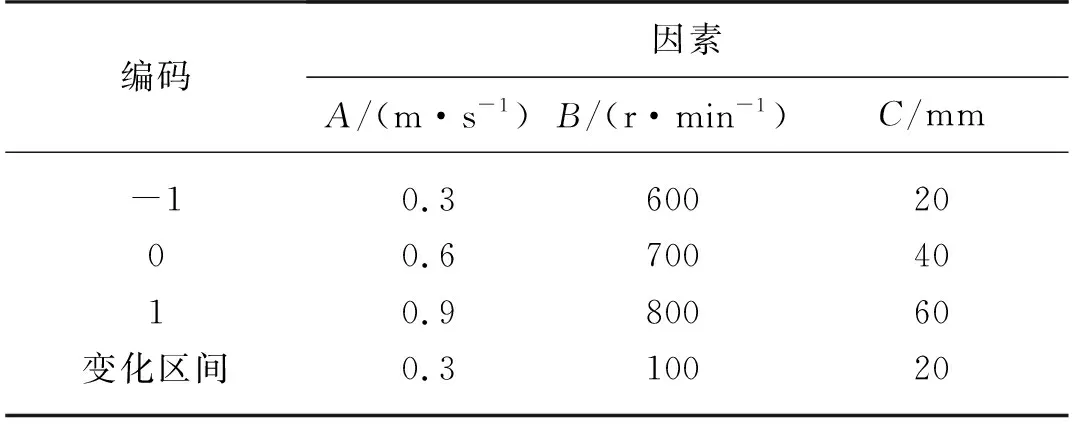
5.2 试验结果分析与回归模型的建立

5.3 响应面分析



6 结论
