自动化绘图背后的计算思维挖掘与培育
2022-06-20刘宏中


摘要:计算思维是信息技术学科的核心素养之一,学生计算思维的习得是需要教师根据学生认知特点和教学内容去设计和深度挖掘的。本文针对编程模块的Python程序结构教学内容,利用Turtle库的绘图功能,让学生在设计图形自动化绘制程序过程中,体验问题分解,引导学生寻找规律,识别重復的模式,表示算法,编写程序。在识别结构、构建结构和驾驭结构的过程中体验和习得计算思维。
关键词:Python;模式识别;编程;计算思维
中图分类号:G434 文献标识码:A 论文编号:1674-2117(2022)12-0070-03
数字技术、数字经济是世界科技革命和产业变革的先机,是新一轮国际竞争的重点领域,因此,提升计算思维,发展信息素养,成为信息技术教育的重中之中。
什么是计算思维?计算思维是利用计算机科学的基本概念解决问题、设计系统和理解人类行为的思维活动。它包括问题分解、物理世界的抽象(根据需要把物理世界的信息抽象成计算机能够理解的数字信息)、寻找规律、识别模式、设计算法。计算思维的培养方式与途径有很多,编程是学生习得计算思维的重要途径之一,计算思维和编写代码是计算机程序解决问题的两个重要环节,计算思维在前,编写代码在后。目前,义务教育阶段的信息技术课中已经有了编程模块,不管是图形化编程还是代码编程,教师都要引导学生体验问题分解、现实抽象、模式识别、算法设计、程序排错等过程,培养学生计算思维。
浙江省义务教育教科书《信息技术》八上的学习内容是Python程序设计,因此,笔者结合第二单元“Python程序基本结构”的教学内容,尝试利用Turtle模块设计程序自动绘制图形,在识别、构建和驾驭结构的过程中帮助学生习得计算思维。
● 过程可视,识别结构
学习编程,首先要理解程序执行过程。为了让学生快速入门,教师可通过编写画图程序,使程序执行过程可视化,在可视化的条件下帮助学生更好地理解程序的结构。
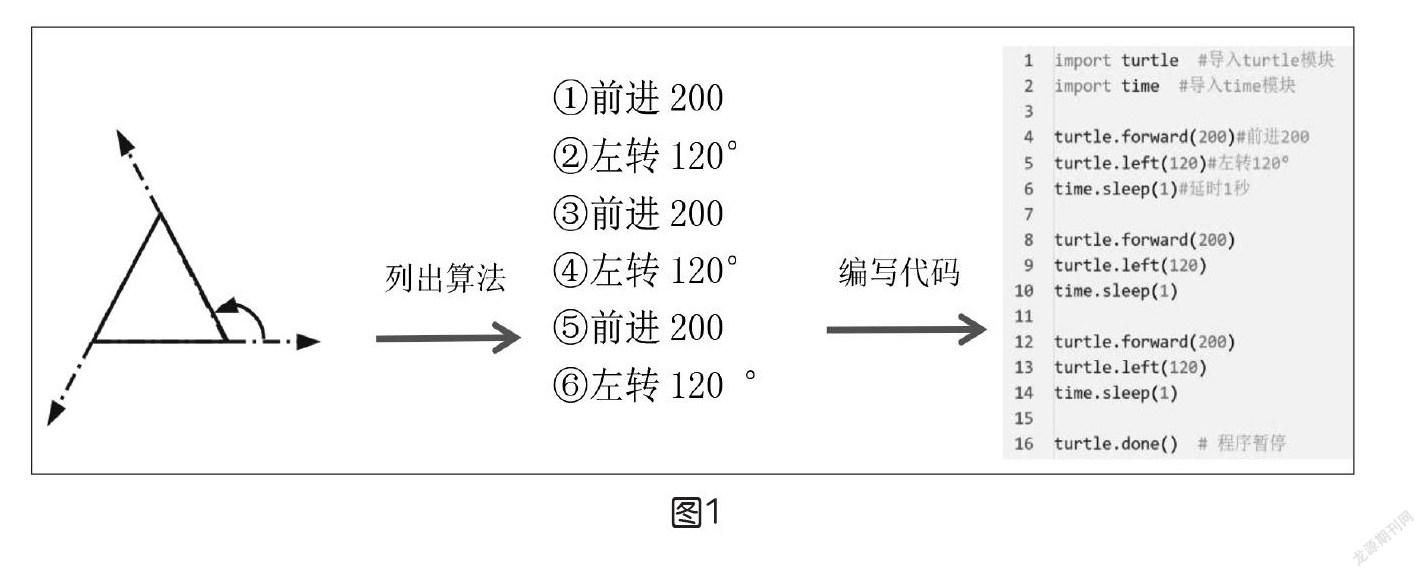
任务1:编程画一个等边三角形。
通过任务分析,总结出画等边三角形的步骤如下:先把画三角形的问题分解为画边和转角两个子问题,然后表示成算法,最后编写程序(如图1)。程序运行就能看到三角形绘制的全过程,从而理解顺序结构,明白程序是由上到下依次执行的。
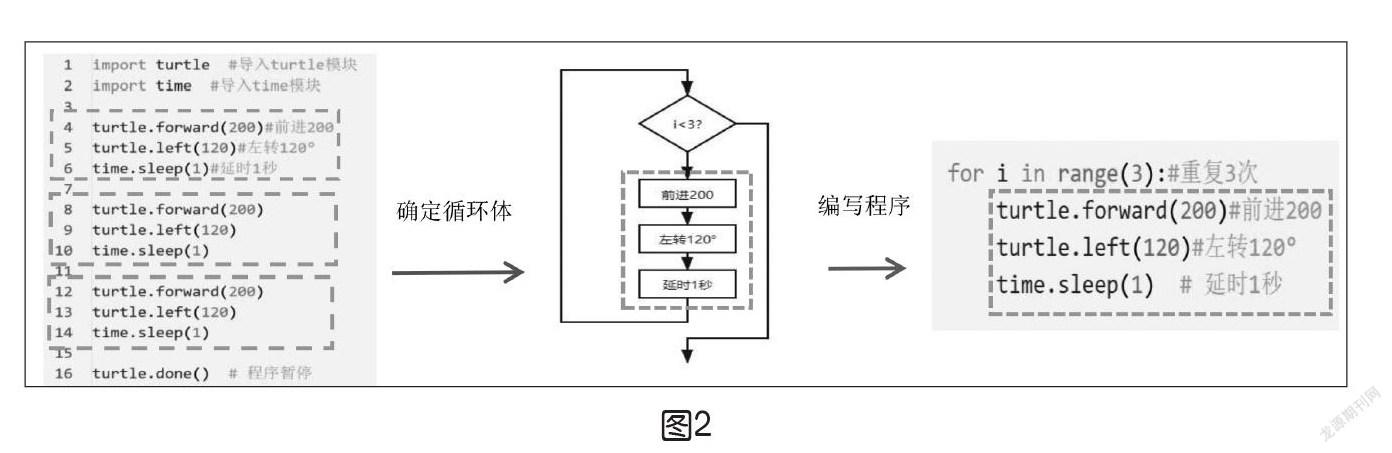
如果用同样的方法编程画一个正方形、正六边形、正六十边形,代码行数就会不断增加,创设认知冲突引入循环结构。
通过观察可以发现,画边、转角、延时的代码一样,不同的是转角的参数与代码行数不同。
教师引导学生找出程序中重复执行的代码,作为循环体根据循环流程用For循环编程,编写出程序(如图2),体会循环结构对减少代码冗余的作用,并引导学生对比程序执行的过程,理解循环结构与顺序结构中的程序执行过程其实是一样的,只是循环结构控制了循环体的执行次数。
同样,要求学生修改图中程序的参数画一个正方形、正六边形、正六十边形。在For循环程序中,只需修改循环次数和转角度数,就能完成相应的图形绘制,调试程序修改参数非常方便。
● 寻找规律,构建结构
任务1中代码的重复是一个非常简单的重复模式,通过前面修改循环次数和旋转角度可以画出多种不同的正多边形,引导学生观察,找出绘制不同多边形程序中的相同点和不同点,分析转角的度数与边数的关系,思考如何使程序变成一个能绘制任意正多边形的程序。
运用变量来概括性描述规律,寻找重复模式,是构建循环的利器。这里的变量就像数学中用字母表示数一样,有助于揭示概念或规律的本质特征,实现对一类问题的抽象。
教师可引导学生通过观察与分析,明确画正多边形的每次转角的度数,即外角的度数。外角的大小可以从内角和定理180-(n-2)*180/n推导出。也可以这样推导:正多边形的外角和为360度,旋转一周回到起始位置,n条边,旋转n次,每次旋转的角度就是360/n。这样,程序就能根据n的取值画出相应的正多边形,变量n就泛指大于3的任何整数。
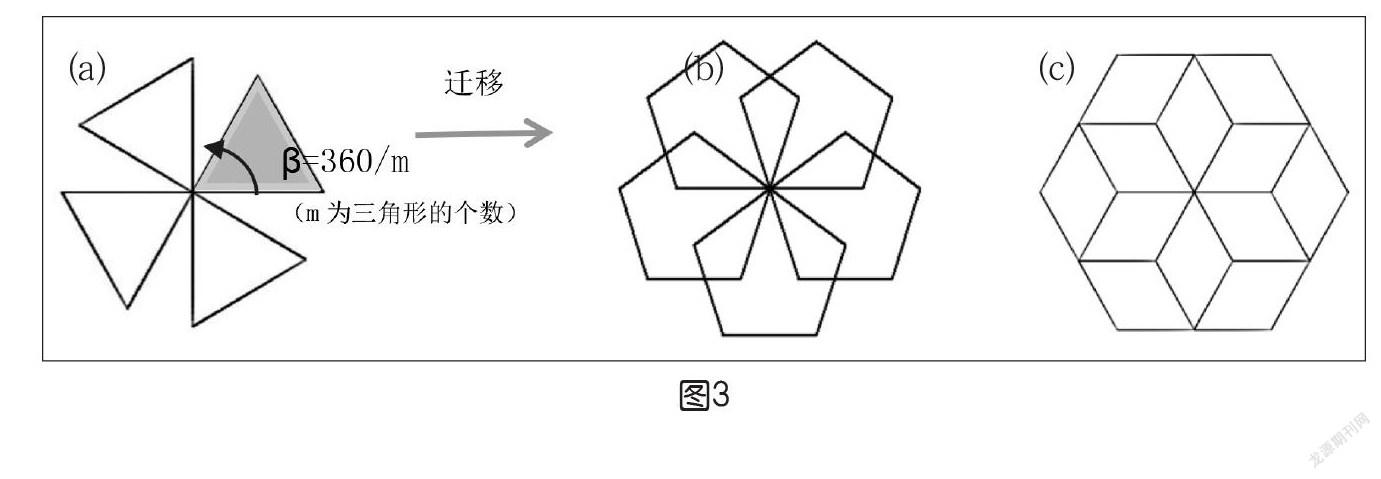
任务2:编程画出图3中的某一个图形。
在拆解复杂问题时,需要遵循置顶向下的原则,从宏观到中观,从中观再到微观,寻找规律,识别重复模式。图3(a)可以理解为一个正三角形重复旋转4次而形成的,因此把宏观的图形的问题分解为画正三角形和旋转角度两个中观问题,由此构建外循环,再考虑中观的正三角形的实现,构建内循环。
由图3(a)迁移可知,图3(b)可以看成由正五边形等角旋转5次而成;图3(c)可理解为正六边形等角旋转6次而成,由于有几条边重合,有点难以辨别。
通过分析发现3个图形的绘制方法相同,可以理解为一个正多边形经过多次重复等角旋转而成,从而形成一个统一的重复模式,流程图与程序如下页图4所示。
● 封装提取,驾驭结构
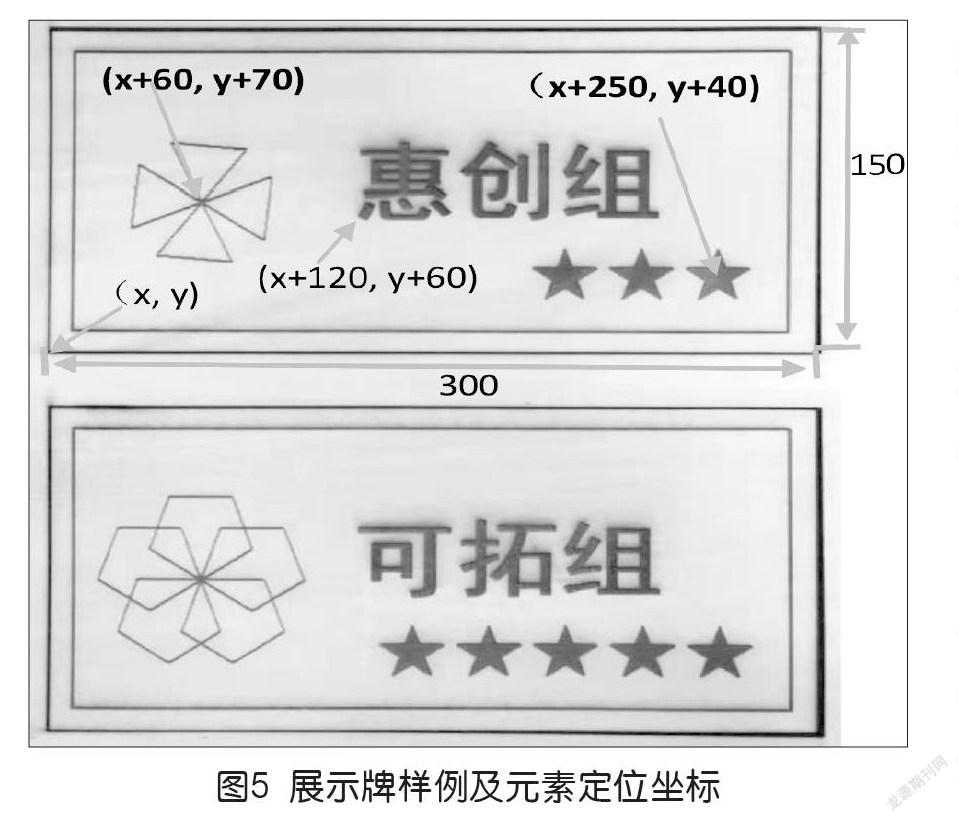
应用计算思维解决问题是培养计算思维的重要途径和最佳方式,临近期末,创客社团需要通过激光雕刻制作一批社团考核展示牌,在激光雕刻之前需要设计图形(如下页图5)。
任务3:编写自动化绘制社团展示牌的程序。
一批展示牌,具体数量暂时不定,要求程序能根据具体要求快速绘制出所需要图形。通过观察分析发现,展示牌都是由LOGO、星级、社团名和矩形框元素组成,其中LOGO图、星级数量和社团名各不相同。由此决定把四个元素的程序分别封装到自定义函数print_rectangle()、print_logo()、print_star()和print_name()中,对可变的元素分别通过传送参数的方式进行改变。
有了元素的自定义函数,只要确定好每个元素的绘制位置就能把展示牌图案绘制出来。
根据展示牌案样式中各元素的相对位置,以外框的左下角位置(x,y)为参照点,内框的左下角位置为(x+10,y+10),LOGO绘制位置为(x+60,y+75),组名绘制的起始点位置为(x+120,y+55),星星从(x+260,y+40)绘制位置开始画,每画完一个向左移动30。
把组名、星级、LOGO类型分别按顺序添加到列表中,在循环中引用列表中的值作为参数传给自定义函数,输入想绘制的展示牌的行数与列数,就能绘制出想要的所有展示图案(如图6)。
计算思维能帮助我们理解计算机世界和AI背后的运行机理,掌握解决大规模复杂问题的思考方法。“计算思维的内涵其实就是一种转换,是人类理解向着机器执行之间的转换,是复杂问题解决向着机器基本操作的转换”,需要运用分层、抽象、封装和迭代去构建结构,设计算法,在平时的教学中,还需要教师去挖掘程序算法与数据中的结构之美。
参考文献:
[1]诸葛越.未来算法:下一个十年赢在计算思维[M].北京:中信出版社,2021,6.
[2]费海明.回归本源:再论信息技术核心素养的养成[R].宁波:江北教育局教研室,2021,11.
作者简介:刘宏中(1970—),男,高级教师,浙江省初中信息技术教材编委。
