长期作用下HRB600钢筋高强混凝土柱轴压性能有限元分析

李志黎 陈从召

摘要：为探讨混凝土长期收缩徐变作用对HRB600钢筋高强混凝土柱轴压性能的影响，利用ABAQUS有限元软件建立1根不考虑长期作用的柱模型试件与12根考虑长期作用的柱模型试件，并进行对比分析，初步探究了纵筋配筋率、混凝土强度和配箍率对构件承载力和峰值应变的影响。分析结果表明：考虑长期作用后，構件承载力减小6.5 %，峰值应变减小15 %，随着纵筋配筋率、混凝土强度、配箍率的增加，构件承载力随之增加，其中配箍率影响最小，进一步在混凝土结构设计规范中柱轴压承载力计算公式基础上，提出考虑长期作用下HRB600钢筋高强混凝土柱轴压承载力修正计算式。

[作者简介]李志黎（1996—），男，在读硕士，主要研究方向为混凝土结构;陈从召（1997—），男，在读硕士，主要研究方向为混凝土结构。

高强钢筋高强混凝土结构具有构件截面尺寸小、增加建筑使用面积、节约材料的优点，目前，国内外学者对配置高强钢筋高强混凝土构件进行了大量的研究[1-3]，其中由于配制HRB600钢筋构件的相关基础性试验研究不足，导致HRB600钢筋难以在实际工程中推广应用 [4]。

长期荷载作用下混凝土由于收缩、徐变效应引起的应力重分布对结构构件受力性能影响显著，陈周熠等[5]进行了钢骨混凝土短柱在长期轴向荷载作用下的试验研究，韩林海、王文达等[6-7]对钢管混凝土柱在长期荷载作用下的受力性能进行了研究，而目前对于高强钢筋高强混凝土构件在长期荷载作用下的受力性能研究较少。

通常将混凝土收缩效应等效为温度荷载进行研究，并采用基于龄期调整有效模量法考虑混凝土的徐变作用[8-9]，然而，通过对前人所作的工作以及一些文献的研究分析可知，按龄期调整有效模量法中采用的折减的弹性模量与实际结构承受持续荷载后弹性模量随龄期增加会有所增加的现象不符[10]，故本文结合文献[10]提出的徐变效应等效温度理论，利用ABAQUS有限元分析软件探究混凝土长期收缩、徐变作用下HRB600钢筋高强混凝土柱轴向受力性能。

1 混凝土长期收缩徐变效应

混凝土收缩可等效为均匀温降作用，混凝土徐变效应参考文献[10]中徐变效应等效温度推导，如式1所示：

式中：t0为混凝土加载龄期;σt0为t0时刻作用于混凝土的常应力;t为混凝土计算龄期;Et0为t0时刻混凝土的弹性模量;φt，t0为加载龄期为t0，计算龄期为t的混凝土徐变系数;E28为混凝土28天弹性模量;α为混凝土热膨胀系数。

本文混凝土长期收缩徐变效应参考混凝土结构设计规范[11]中混凝土10年收缩应变终极值ε与10年徐变系数终极值φ，如表1所示，其中，混凝土加载龄期为28天，热膨胀系数为1×10-5/℃，设计轴压比为0.4。

2 有限元分析

2.1 模型建立

基于有限元软件ABAQUS对HRB600钢筋高强混凝土柱进行建模，有限元部件为混凝土柱、钢筋笼、钢板，尺寸设置与文献[12]一致。

2.1.1 材料本构关系

采用ABAQUS中损伤塑性模型进行非线性计算，混凝土本构关系参考过镇海模型[13]，钢筋采用二折线模型，硬化段斜率为0.01，混凝土损伤因子参考文献[14]中的推导计算。

2.1.2 相互作用与约束

不考虑钢筋混凝土之间的粘结滑移，所有钢筋内置于混凝土中，定义参考点并与钢板耦合，加载端钢板与垫块钢板分别与混凝土柱上下端面绑定，模型底部为固定约束。

2.1.3 单元与网格

混凝土采用C3D8R单元，钢筋采用T3D2单元，使用ABAQUS中结构网格划分技术，网格密度为60 mm。

2.1.4 荷载

采用单调位移加载方式，在顶部参考点施加竖向位移，当考虑钢筋混凝土柱长期收缩徐变作用下的轴向受力性能时，首先根据设计轴压比在柱顶施加均布应力，然后将收缩徐变作用等效为温差效应，对混凝土柱进行整体均匀降温，最后进行位移加载。

2.1.5 模型验证

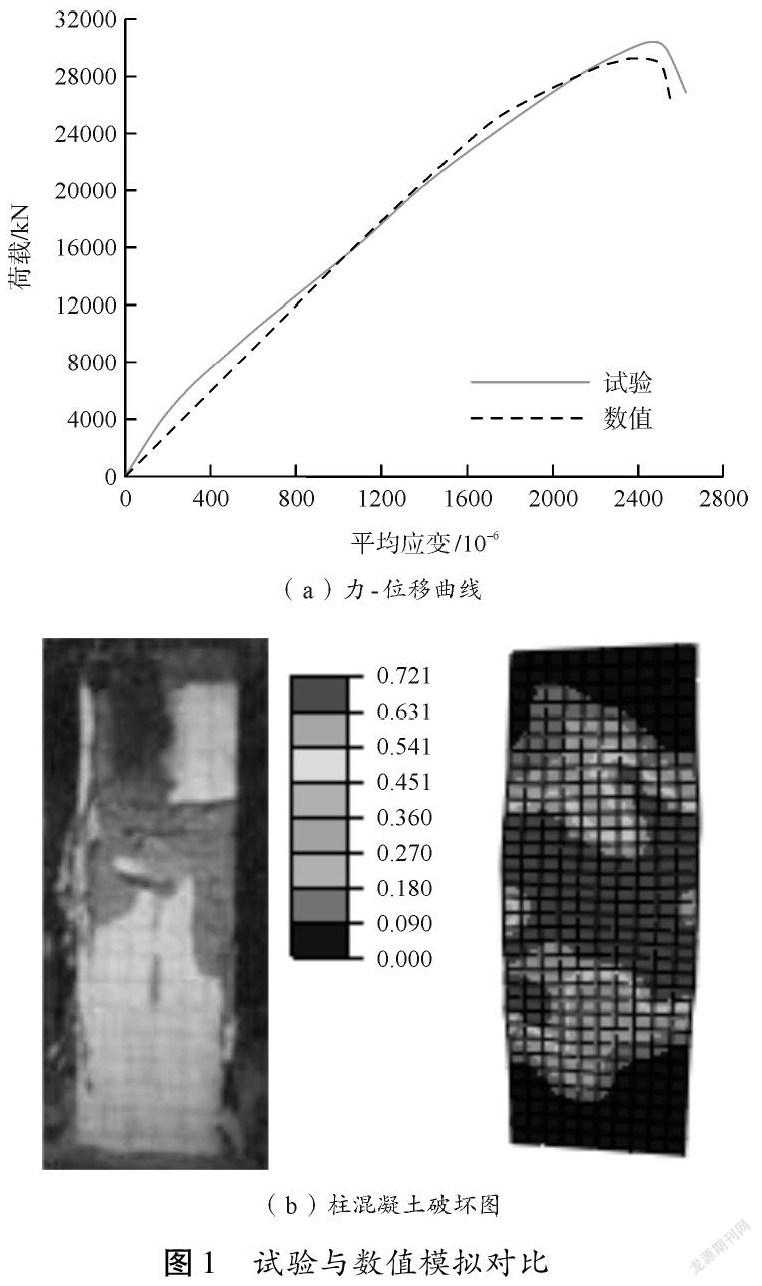
选取文献[12]中HRB600钢筋高强混凝土柱（Z1）进行模拟，对比分析构件的力-位移曲线和破坏图，如图1所示，发现数值模拟力-位移曲线与试验曲线吻合较好，且混凝土受压损伤云图与试验柱损伤发展较为一致，可验证有限元模型的合理性。

2.2 对比分析

由GB 50010-2010（2015版）《混凝土结构设计规范》（以下简称为《规范》）11.4.16[11]知，一级抗震等级的不同结构体系轴压比限值在0.65左右，且对于高强混凝土结构，轴压比限值宜减小0.1，故以下对比分析设计轴压比为0.4时HRB600钢筋高强混凝土柱长期收缩徐变作用下的轴向受力性能，如图2所示， 当不考虑混凝土长期收缩徐变作用时，HRB600钢筋高强混凝土柱极限承载力为29 231 kN，峰值应变为2.358×10-3;考虑长期收缩徐变后，混凝土柱极限承载力为27 333 kN，同比减小6.5 %，峰值应变为2.005×10-3，同比减小15.0 %。

2.3 参数分析

在试验验证合理基础上，初步探究纵筋配筋率、混凝土强度、配箍率对长期作用下HRB600钢筋高强混凝土柱轴压性能影响，并建立12个有限元模型试件进行分析，试件参数设置如表2所示。

2.3.1 纵筋配筋率

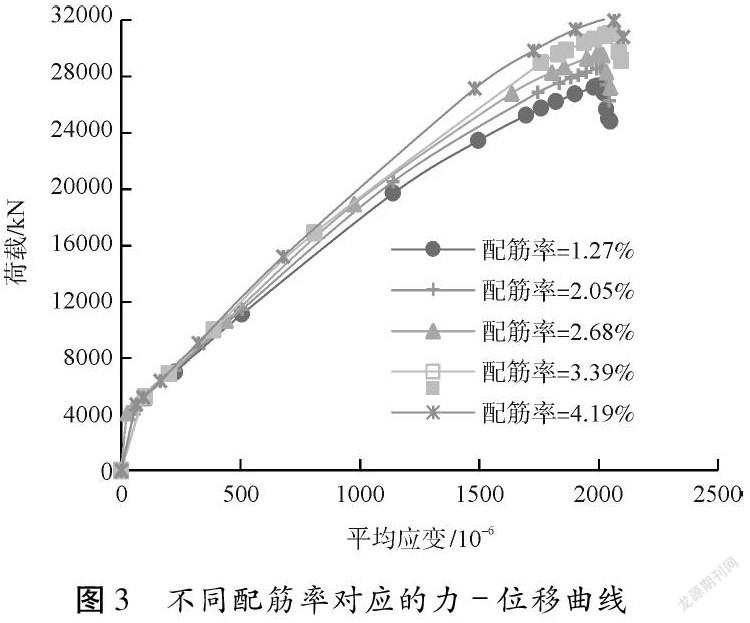
试件GQZ1～5的纵筋配筋率依次为1.27 %、2.05 %、2.68 %、3.39 %、4.19 %，不同配筋率对应的柱力-位移曲线如图3所示。随着纵筋配筋率的增加，混凝土柱的极限承载力不断增加，而峰值应变变化不大，由表3知，峰值应变标准差为20.4×10-6，纵筋配筋率对高强混凝土柱的增强主要体现在轴向受压强度上，对其变形性能影响较小。

2.3.2 混凝土强度

选取C100、C80、C60、C40等级的混凝土材料进行分析，为与试验结果保持一致，其轴心抗压强度值选用试验研究中所用混凝土的实测强度值，即分别采用82.2 MPa、69.7 MPa、53.0 MPa、40.0MPa[12]，试件GQZ1、试件GQZ6～8分别对应不同混凝土強度等级，其力-位移曲线如图4所示。

混凝土强度增加，混凝土柱极限承载力与峰值应变均显著增加，由表3知，相比C40混凝土，C60、C80、C100混凝土柱承载力依次提高24.3 %、56.5 %、76.8 %，峰值应变依次增加2.8 %、13.9 %、28.1 %。

2.3.3 箍筋配筋率

试件GQZ1、GQZ9～12的配箍率依次为0.57 %、0.76%、1.15 %、1.53 %、2.29 %，不同配箍率对应的柱力-位移曲线如图5所示。

随着配箍率增加，混凝土柱极限承载力与峰值应变均有增加，如表3所示，参数纵筋配筋率对应的峰值荷载标准差为1 672 kN;参数砼强度对应的峰值荷载标准差为5 143 kN;参数配箍率对应的峰值荷载标准差为424 kN，相比于纵筋配筋率和混凝土强度，配箍率对混凝土柱的承载力影响较小。

3 轴压承载力计算

“规范”[11]规定钢筋混凝土轴压构件正截面承载力计算式为：

当不考虑混凝土长期收缩徐变时，戎贤、张建伟等通过试验与有限元软件对HRB600钢筋高强混凝土柱轴压承载力进行了研究，并验证了式（2）的适用性[5，13]，当考虑混凝土长期收缩徐变时，参数纵筋配筋率、混凝土强度、配箍率对HRB600钢筋高强混凝土柱轴压承载力影响趋势与文献（不考虑混凝土收缩徐变）[13]中各参数影响趋势较为一致，即随着纵筋配筋率、混凝土强度、配箍率的增加，构件承载力随之增加，且配箍率影响较小，故根据上文有无收缩徐变作用混凝土柱承载力对比分析，提出长期作用下HRB600钢筋高强混凝土柱轴压承载力计算修正式（3）：

式中：β为考虑长期作用后构件承载力折减系数。

基于以上理论分析，对试件GQZ1～5、试件GQZ7～12进行无收缩徐变作用承载力分析，并与考虑混凝土收缩徐变作用柱承载力对比，如表4所示。

由表4知，随着参数的变化，折减系数βi的标准差为0.014，分布较为集中，长期作用后构件承载力折减系数β可参考βi的期望值0.928，故式（3）可变化为：

式（4）中HRB600钢筋屈服强度设计值参考文献[4]取500 MPa，修正后的承载力理论计算值与有限元计算值对比如表5所示。

表5中F2/Nu均值为1.21，变异系数为0.016，可验证考虑长期作用的HRB600钢筋高强混凝土柱轴压承载力修正公式的适用性。

4 结 论

（1）考虑混凝土长期收缩徐变作用后， HRB600钢筋高强混凝土柱轴压承载力与峰值应变均有减小。

（2）纵筋配筋率、混凝土强度、配箍率越大，长期作用下HRB600钢筋高强混凝土柱承载力越大，相比于纵筋配筋率和混凝土强度，配箍率对构件的承载力影响较小。

（3）提出考虑长期作用下HRB600钢筋高强混凝土柱轴压承载力修正计算式，试验与理论比期望值为1.21，变异系数为0.016，该式具有足够的安全储备。

参考文献

[1] 罗绍华. 600MPa级钢筋混凝土偏心受压构件受力性能试验研究[D].南京：东南大学， 2013.

[2] Sener S ， Barr B I G ， Abusiaf H F . Size Effect in Axially Loaded Reinforced Concrete Columns[J]. Journal of structural engineering， 2004， 130（4）： 662 - 670.

[3] Cusson D ， Paultre P . High-Strength Concrete Columns Confined by Rectangular Ties[J]. Journal of Structural Engineering， 1998， 120（3）：783-804.

[4] 戎贤， 申成成， 张健新. HRB600钢筋混凝土短柱轴压性能试验研究[J].混凝土，2020（2）：28-32.

[5] 陈周熠， 代堂珍， 雷鹰，等.钢骨混凝土短柱在长期轴向荷载作用下的试验研究[J].工程力学， 2015，32（8）：82-87.

[6] 韩林海，杨有福，刘威. 长期荷载作用对矩形钢管混凝土轴心受压柱力学性能的影响研究[J]. 土木工程学报，2004，37（3）：12-18.

[7] 王文达， 邹爱华， 张鹏鹏. 长期荷载作用下矩形钢管混凝土轴压短柱力学性能[J].公路交通科技， 2011， 28（7）：73-78.

[8] 万小妹. 超长钢筋混凝土框架结构温度（收缩）应力非线性分析与设计对策研究[D].南昌：南昌大学， 2011.

[9] 吴超. 间接作用下超长混凝土结构无缝设计与施工关键技术研究[D]. 南京：东南大学，2018.

[10] 赵立勇. 基于等效温度法的预应力混凝土连续梁桥的徐变效应[D].北京：北京交通大学，2013.

[11] 混凝土结构设计规范： GB50010-2010[S].北京： 中国建筑工业出版社，2010.

[12] 张建伟，夏冬瑞，乔崎云，姜立伟.HRB600级钢筋高强混凝土柱的轴心受压性能[J].工业建筑，2017，47（11）：77-83.

[13] 过镇海.混凝土的强度和本构关系：原理与应用[M].北京：中国建筑工业出版社，2004.

[14] 张战廷，刘宇锋.ABAQUS中的混凝土塑性损伤模型[J].建筑结构，2011，41（S2）：229-231.