基于ABAQUS的隧道锚极限承载力及影响因素研究
2022-06-19席晨刘芳炜
席晨 刘芳炜

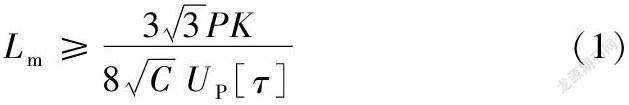
摘要:文章以悬索桥隧道式锚碇(隧道锚)室内模型试验为参考,利用Abaqus软件对隧道锚的受力过程进行数值模拟,研究隧道锚的极限承载力,以及圆台形状的锚塞体的长度和坡比对极限承载力的影响。数值模拟结果表明,增大锚塞体的长度或坡比,均可提高极限承载力,说明围岩与锚塞体的接触作用是提高承载力的关键。
[作者简介]席晨(1994—),男,在读硕士,研究方向为隧道锚承载特性。
1 隧道锚介绍
大跨径悬索桥锚碇形式主要有自锚式和地锚式两种,其中地锚式又分为隧道式锚碇和重力式锚碇。隧道式锚碇(隧道锚)作为悬索桥的锚固形式之一,主缆锚固在岩洞中的混凝土锚块(锚塞体)中,荷载由主缆传递给锚块,再通过锚块与围岩的接触作用,将荷载传递到围岩中去,调动附近大范围的围岩共同参与抗拔作用,与重力式锚碇单独依靠锚块自重来平衡主缆荷载相比,其混凝土用量更少,开挖方量更小,工程造价更低[1]。由于隧道锚的锚固特点,一般适用于岩体完整性较好的地区。
隧道锚是由锚塞体和周围岩体组成的一个复杂体系。由于隧道锚的受力变形涉及锚塞体与周围岩体的相互作用,因此其力学行为非常复杂。目前尚无完整的理论体系和计算方法。多以模型试验和数值模拟为主,刘锦[2],卫军[3]分别使用不同的计算软件模拟了隧道锚从施工开挖到荷载施加的整个过程,研究其稳定性。本文限于条件,仅使用Abaqus软件,以室内模型试验为参照,对荷载施加阶段进行模拟,研究隧道锚的极限承载力及锚塞体的长度和坡比对极限承载力的影响。
2 模型设计
2.1 物理力学参数
隧道围岩按理想的弹塑性材料考虑,服从Mohr-Coulomb屈服准则,锚塞体按线弹性材料考虑,在本试验中,考虑到研究目的以及锚塞体相较于围岩的尺寸差,假设试验中锚塞体不会破坏,因此其弹性模量取值较大。室内模型试验具体参数见表1。
2.2 几何参数
Abaqus建模中围岩用长方体模拟,锚塞体用圆台模拟,考虑对称性,只需建立半模型。模型以室内模型试验[4]为参照,具体设计如图1,从截面处可以更好的观察锚塞体的竖向位移情况和围岩的塑性变形。考虑到荷载由锚塞体传递至围岩的影响范围,围岩尺寸选为2 m×1 m×1 m,在围岩中预留锚塞体的位置。
锚体截面尺寸设计要求[1]。
(1)锚体截面足够大,满足主缆散索后锚固空间的需要。
(2)锚体截面不能太大,以致使左右锚体距离过近,使锚体间围岩扰动严重,从而造成其强度降低过多。
(3)锚体截面的外轮廓要有利于岩体开挖阶段的稳定。
长度尺寸的选取,朱玉[5]根据四渡河大桥隧道锚设计的研究成果,建议一個近似计算公式:
式(1)中:P为主缆拉力,K为锚碇安全系数,C为系数,取0.1~0.12之间,UP为锚体截面周长,[τ]为容许抗剪强度,偏安全取黏聚力,Lm为锚体长度。
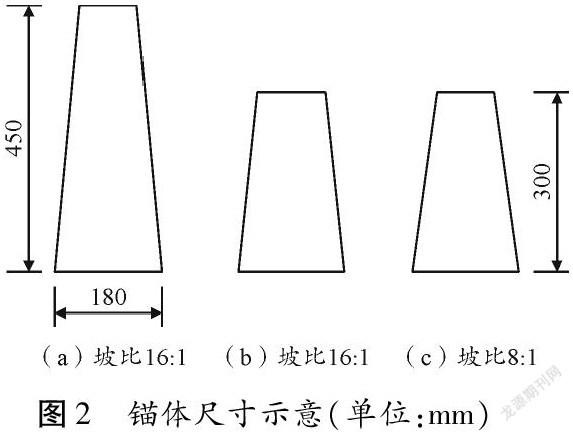
本次数值模拟中并未严格按照上述原则进行锚塞体设计,具体设计情况见图2。霍剑雄[6]提到变截面锚塞体的“楔形效应”即锚塞体在拉拔荷载作用下产生拉力方向的变形,此时锚塞体与围岩相互挤压,围岩和锚塞体接触面之间产生巨大的摩擦力使得锚塞体将带动周围的围岩也产生变形。变截面锚塞体的长度和坡比会影响“楔形效应”进而影响极限承载力,因此通过A、B两组对比可研究锚塞体长度对极限承载力的影响,B、C两组对比研究坡比对极限承载力的影响。
3 模型建立
按照图1、图2建模,材料属性参数由表1中模型的参数决定。在锚塞体底面中点设置监测点观察其竖向位移。围岩和锚塞体均采用C3D8R单元划分网格,在锚塞体与围岩接触区域适当增大网格密度以提高计算精度。围岩模型底面)约束三向位移,侧面约束法向位移,上表面不作约束;锚塞体仅约束可视截面的法向(Z向)位移。
锚塞体与围岩的接触选择面与面离散方法,围岩作为主控面,锚塞体为从属面。定义接触面上法向模型为“硬”接触[7],只有在接触时才能传递法向压力P,允许出现脱离情况,脱离时不传递法向压力;切向模型为“罚”接触[7],当接触面处于闭合状态(即有法向接触力P)时,接触面可以传递切向应力,根据汪海滨[8]所做试验,混凝土与岩体的接触面摩擦系数取0.2。
荷载工况:先施加重力再施加荷载,设计荷载为P=288 N。悬索桥主缆经散索鞍分散后均匀锚固于锚塞体中,在承受主缆拉力前一般要通过这些锚索预先在锚塞体前后端面施加略大于设计荷载的预应力,因此在主缆拉力作用下尤其是在超载阶段,锚塞体的实际受力部位是后端面[9],因此将设计荷载处理成均布压力采用后推法施加于锚塞体底面,并逐级增大,增量2P,直到围岩破坏,隧道锚达到极限承载力。需要注意的是锚塞体的自重对抗拔作用也有贡献,因此其底面并未约束,但围岩底面有约束,所以仅在自重作用下,锚塞体会向下移动,根据接触关系,此时围岩对锚塞体的位移无任何阻力,会导致围岩和锚塞体发生较大的相对位移而无法计算,因此在施加重力的同时在锚塞体底面施加设计荷载1P以减小其自重下的位移。
4 结果与分析
4.1 破坏判据
目前,数值模拟中判断围岩破坏的评价标准主要有3种[7]:
(1)以数值计算收敛与否作为评价标准。
(2)以特征部位的位移拐点作为评价标准。
(3)以是否形成连续的贯通区作为评价标准。
在本文中,以第二种标准作为主要判据,即后锚面的位移情况,可以预测的是当围岩破坏时,位移曲线会发生突变,以第一、第三标准作为辅助参考。
4.2 后锚面位移情况
将锚塞体后锚面在各级荷载作用下的位移值绘制曲线图,如图3~图5所示。
由图3~图5可以看出,位移曲线有着相同的趋势,斜率越来越大,即后锚面的位移变化速度随着荷载的增大逐渐加快,不同的是,图3、图4在曲线末端有着比较明显的拐点(曲线斜率突变),图5拐点不明显,这可能与锚塞体的坡比有关,取倒数第二点为该条曲线拐点。0BDB1778-9C48-40AF-B6C8-47DE25058242
4.3 围岩塑性区分布
A组(450 mm,坡比1∶16)锚塞体塑性区发展情况如图6~图8所示。
从图3~图5可以看到A组试验中,围岩塑性区的发展情况,图6,荷载5P时围岩由弹性转为塑性变形,在后锚面两侧最先出现塑性区域,随着荷载的增大,塑性区由后锚面两侧向上逐渐发展,图7,31P时锚塞体两侧已全部转为塑性区,此时锚塞体顶部还未出现塑性变形,图8,43P计算不收敛时,可以看到锚塞体前锚面两侧以及上部区域开始出现塑性区域,基本形成包围锚塞体的塑性区。
B、C两组试验仅给出破坏时的塑性云图(图9、图10)。
从图9、图10中可以看到,这2组最终的塑性区并未发展到锚塞体顶部以上的区域,且C组(300 mm 1∶8) 的塑性应变要大于B组(300 mm 1∶16).
4.4 分析讨论
荷载位移曲线斜率的不断增大,说明在相同荷载增量下,位移的变化越来越大,这是因为,荷载不断增大,由锚塞体通过接触传递给围岩的荷载也就越大,围岩中的塑性区在渐增荷载的作用下也在不断扩大,围岩的强度逐渐降低,对锚塞体的阻挡作用越来越小,相应的,锚塞体的位移在同荷载增量下就会越来越大,直到塑性区贯通整个接触面,围岩破坏,隧道锚达到极限承载力。
隧道锚的极限承载力由荷载位移曲线图,结合破坏判据,可认为拐点处的荷载值即极限承载力,由计算结果:A组为928.527 kN,B组为837.939 kN,C组为928.527 kN,显然A组=C组>B组,对比A、B说明相同坡比下,锚塞体越长,其承载力就越大,对比B、C组,说明相同长度下,坡比越大,承载力越大,结合A、B、C 3组,可以看到无论是增大长度或增大坡比,都增大了锚塞体与围岩的接触面积,可以调动更大范围的围岩参与抗拔作用,从而提高了隧道锚的承载力,C组同极限荷载下的最终位移小于A组是因为C组的坡比大,可影响的围岩范围大于A组,相同的荷载增量作用在C组更大范围的围岩上,所产生的位移自然小,对比A、C 2组可以看到,A组坡比小,长度大则更依赖于切向摩擦力提高承载力,而坡比大,长度小的C组则更依赖于法向的压力来提高极限承载力。
根据荷载位移曲线以及塑性区的发展情况,可以大致的将隧道锚的受力过程分为3个阶段,第一阶段,弹性变形阶段,对应位移曲线中最开始的平缓段,以及塑性云图中塑性变形为0(A组<5P)的阶段。第二阶段,塑性发展阶段,对应位移曲线斜率渐增段,塑性云图中塑性区域逐渐发展阶段(A组5P~31P)。第三阶段,破坏阶段,对应位移曲线拐点后的破坏段,塑性云图中塑性区贯通整个锚塞体(A组41P~43P)。B,C 2组的塑性区未完全覆盖整个锚塞体,猜测原因与锚塞体长度有关。同长度下C组的塑性应变大于B组,这与坡比有关,同高度下坡比大,锚塞体与围岩的接触面就大,承载力高,C组通过接触传递给围岩的荷载大于B组,相应的塑性变形就大。
5 结论与展望
(1)本文所模拟的隧道锚极限承载力为A组:41P; B组:37P;C组41P。
(2)保持坡比不变,增大锚塞体长度可提高承载力。
(3)保持长度不变,增大锚塞体坡比可提高承载力。
通过本文的讨论可以发现,锚塞体的形态影响接触面积,而岩-锚之间的接触作用对隧道锚的极限承载力很大影响,在此仅讨论了坡比和长度的影响,围岩与锚塞体之间相互作用模型有待研究。
参考文献
[1] 何永龙.隧道锚锚塞体优化设计[J].工程设计,2018:199-211.
[2] 刘锦.悬索桥隧道锚数值模拟分析研究[D].重庆:重庆交通大学,2010.
[3] 卫军,李昊,杨曼娟,等.基于Abaqus平台的四渡河悬索桥隧道锚围岩稳定性分析[J].岩石力学与工程学报,2005,24(增1):4894-4899.
[4] 张琪.悬索桥隧道锚受力特性及极限承載力的试验研究[D].成都:西南交通大学,2019.
[5] 朱玉,彭远程.悬索桥隧道锚设计[J].公路.2007,11:21-26.
[6] 霍剑雄,杨星宇,郑升宝,等.基于楔形效应得隧道锚锚体长度设计探讨[J].公路交通技术,2018,34(1):67-70.
[7] 费康,Abaqus岩土工程中实例详解[M].北京:人民邮电出版社,2017.
[8] 汪海滨,高波.隧道式复合锚碇的作用机理[J].西南交通大学学报 2005,40(6):759-764.
[9] 江南.铁路悬索桥隧道式锚碇承载机理及计算方法研究[D].成都:西南交通大学,2014.
[10] 汪海滨,高波.预应力锚索荷载分布机理原位试验研究[J].岩石力学与工程学报,2005,24(12):2113-2118.0BDB1778-9C48-40AF-B6C8-47DE25058242
