钢-混组合梁斜拉桥风致抖振响应分析
2022-06-19唐文斌钟德超潘良杨镇宇
唐文斌 钟德超 潘良 杨镇宇









摘要:文章对某钢-混组合梁斜拉桥进行了风致抖振响应分析。首先通过计算流体力学软件对桥梁进行气动分析得到静力三分力系数,再分析桥址风场资料并根据规范采用风谱,利用谱分解法得到风谱时程,基于准定常气动理论将得到的风谱时程转换为气动力时程。通过编程软件与有限元软件结合来模拟求解桥梁自然紊流风场下的抖振响应。结果表明:桥塔在最大悬臂状态出现最大抖振内力与位移RMS值;梁体在+3°攻角工况下有最大响应,最大悬臂阶段在边跨1/2处有最大位移RMS值,在中跨1/4处截面有最大内力RMS值;成桥阶段在主跨跨中有最大位移RMS值,在塔1处截面有最大内力RMS值;经分析该桥具有良好的抗风性能。
[作者简介]唐文斌(1978—),男,本科,高级工程师,研究方向为大跨度桥梁;钟德超(1983—),男,本科,工程师,研究方向为大跨度桥梁;潘良(1996—),男,硕士,研究方向为大跨度桥梁;杨镇宇(1996—),男,硕士,研究方向为大跨度桥梁。
近年来,随着桥梁跨度的提升,桥塔桥墩的高度逐步增加,其刚度和阻尼有所降低,对风的敏感性也愈来愈大,故对其抗风问题的研究显得尤为重要。研究者一般采用增大阻尼,安置调质阻尼器,或采纳恰当的整流装配,如整流板等方法控制涡激振动响应;对矩形截面采取倒角的方法限制升力曲线的斜率,加大整体结构刚度,提高弯曲频率等方法来控制驰振,经由断面优化和提高桥梁结构刚度,大跨度桥梁颤振现象已经得到避免;但脉动风导致的桥梁抖振问题则日益突出[1-3]。
桥梁的抖振是指其在紊流场中出现的限幅随机振动,其产生的风速低、频率高,可能会导致桥梁部分构件的疲劳。抖振响应对结构本身通常不会产出灾难性的损伤,但抖振响应在施工阶段可能影响的施工安全,同时在成桥阶段,车辆和行人的舒适度和桥梁构件的使用寿命会受到影响。桥梁脉动风抖振计算中经常采用谱分解法原理进行数值模拟分析[4-5] 。
1 工程背景与模型建立
1.1 工程背景
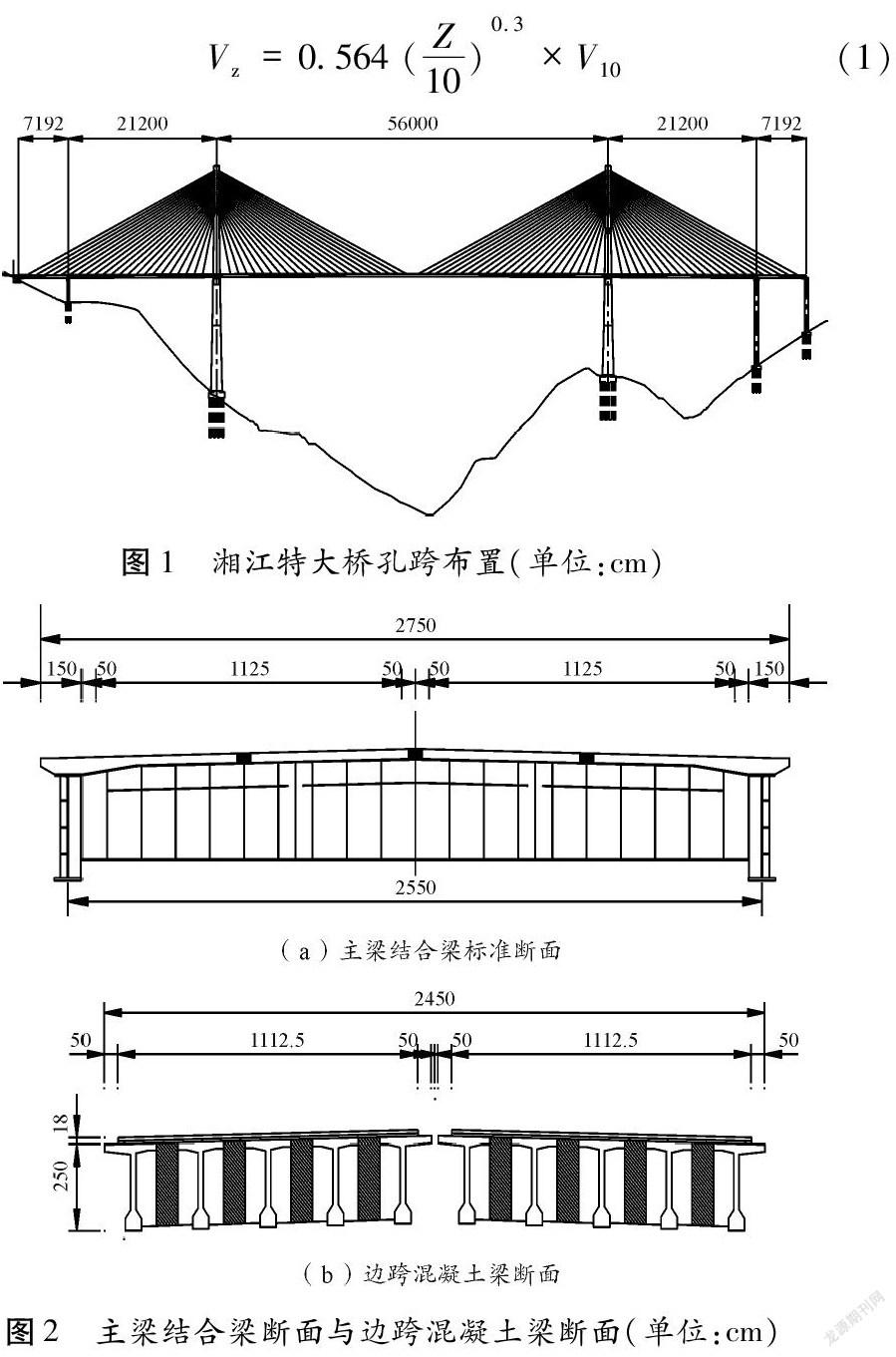
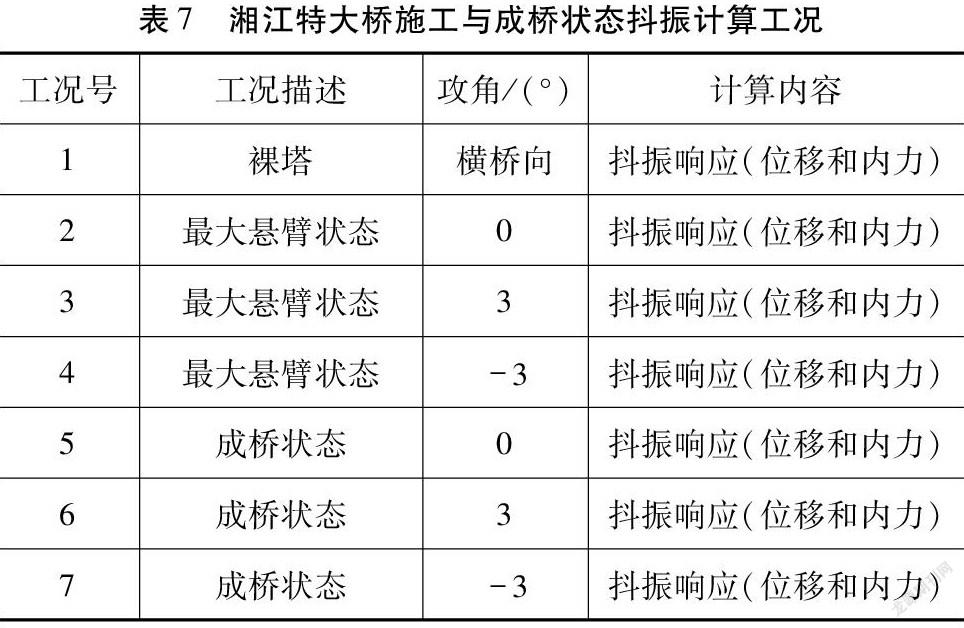
本文对遵余高速湘江特大桥为进行风致响应分析,该桥全长1 658 m,主桥为组合梁斜拉桥,跨度布置为284+560+284=1 128 m,两侧边跨采用对称跨径布置,余庆侧跨径组合为(72+212)=284 m,遵义侧边跨跨径组合为(212+72)=284 m,主桥主梁采用钢-混组合梁,索塔采用A型混凝土塔,辅助墩和过渡墩采用薄壁空心结构;该方案起点不设引桥,遵义侧主桥终点接装配式预应力混凝土40 mT梁,引桥跨径组合为3×40+3×40+3×40+4×40=520 m,引橋桥墩有空心薄壁墩和柱式墩,桥台采用重力式桥台(图1、图2)。
大桥所在区域为山谷地形,按照JTG/T 3360-01-2018《公路桥梁抗风设计规范》,地表粗糙度属于其中的D类,地表粗糙度系数α=0.3,地表粗糙度高度z0=1.0 m。据全国基本风速分布图来确定该桥址处基本风速为24.9 m/s。桥址处的风速剖面满足指数律分布,距离底部地面高度Z处的均匀风速可按下式计算:
1.2 桥梁有限元模型
采用有限元软件ANSYS建立该桥的空间有限元分析模型,主梁结构采取空间梁单元,斜拉索采取空间杆单元。桥塔结构采取空间梁单位(图3)。表1为主要构件材料参数。
2 桥梁风致抖振响应
2.1 桥梁动力特性
采用所建立的全桥结构模型,针对该桥的成桥状态进行动力特性分析,得到表2列出部分模态数据。
2.2 静三分力系数
静三分力系数是用来表示结构断面在定常风作用下所受荷载大小的无量纲量,揭示了风对于桥梁结构的定常气动力作用。风轴坐标下阻力系数CD、升力系数CL以及力矩系数CM定义为[6-7]:
FD、FL和MZ分别表示单位长度梁段的阻力、升力和力矩;ρ表示空气质量密度,取ρ=1.225 kg/m3;U表示来流风速;气动力系数计算选择H和B作为特征长度,H和B分别表示桥面的水平投影高度和竖直投影宽度,分别为3.8 m和28.0 m。
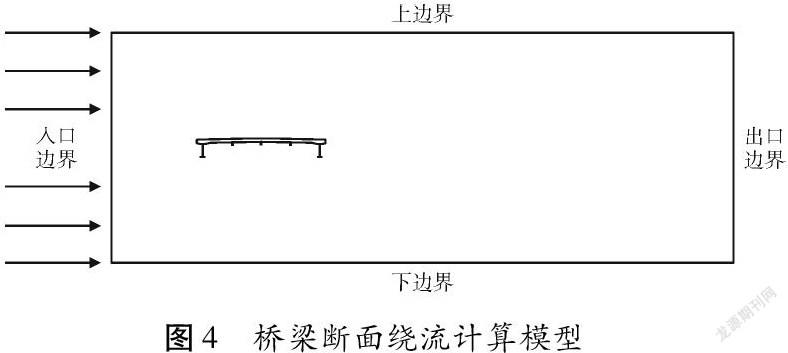
本文利用FLUENT模拟典型断面的二维流场[8-10]。如图4所示桥梁断面处于矩形的计算域中,流场的左侧边界采用速度入口,右侧边界采用压力出口。流场上下边界为对称边界,可以忽略其对流场的影响。整个流场计算区域的宽度为梁截面宽度10倍,高度为梁高的36倍。首层网格单元厚度为0.1 mm,单元厚度自内而外等比递增,在边界层网格外的固定网格区域内,通过定义的网格尺寸函数的使单元网格增长率小于1.05。对梁截面附件的流场网格进行局部加密,并且由内向外进行过度,使网格在满足计算要求的同时保证计算效率,最大网格尺寸为0.05 m。网格数约30万。数值计算雷诺数Re=2×106(表3、图5)。
2.3 风谱与力谱的数值模拟[10-13]
桥梁脉动风抖振计算中,常采用谱解法原理进行数值模拟分析。
把脉动风作为高斯平稳随机过程考虑,对其谱密度函数Cholesky分解,根据Shinozuka理论得到风速时程可表达为:
式(5)中hjm(qΔt)可采用快速傅立叶变换方法进行计算,从而降低计算成本。
风速脉动分量的功率谱函数代表紊流中相应频率所作的贡献。本文采用规范建议的Kaimal-Simiu风速谱。其中水平脉动风谱为:
式中:Su(n)为脉动风的水平方向功率谱密度函数;n为风的脉动频率(Hz);f为相似率坐标,也称莫宁坐标,f=nZU(Z);u为气流摩阻速度。
式中:Sw(n)为脉动风的竖直方向功率谱密度函数;其余各值定义同式(7)。
对于斜拉桥,模拟主要考虑主梁的横桥向脉动风u和竖向脉动风w,以及主塔和斜拉索的横桥向脉动风速u。研究采用Matlab软件编程产生的桥址区结构处脉动风速时程,模拟计算的主要参数见表4。采用指数率对不同高度处的风速进行计算。最后模拟得到成桥期设计风速35.5 m/s下的主梁和桥塔上代表位置的脉动风速时程图6为部分代表位置横向脉动风速时程。
采用准定常气动理论将脉动风速时程转换为荷载时程。本文中桥梁的主梁部分仅考虑正交风的升力、阻力和扭矩,对于桥墩、桥塔及斜拉索等处的风力作用点,仅需考虑风荷载产生的阻力。在本研究中采用西南交通大学对湘江特大桥断面的气动导数计算的结果,并通过有限元软件ANSYS中的27号单元(MATRIX27)分别模拟主梁节点上的气动刚度和气动阻尼(表5、表6)。
本文为得到不同阶段桥梁在不同条件下的风致位移和内力,包括不同的施工态和风攻角。最终湘江特大桥颤抖振时程计算将有7个工况,其对应的工况条件和分析内容如表7所示。
将抖振力时程荷载与静风荷载同时施加于桥梁结构有限元模型上。采用ANSYS进行结构的瞬态动力学时程分析,并采相应的结果后处理程序提取桥梁结构的抖振响应时域分析结果。计算时长为600 s,间隔0.1 s。考虑到几何非线性对于抖振结构的影响,在计算过程中考虑应力刚化条件和大变形条件。主梁的抖振位移提取竖向位移和横桥向位移,桥塔结构为横桥向位移。
2.4 施工与成桥状态抖振位移响应
抖振内力计算时,对于施工和成桥状态取设计基准风速(35.5 m/s)作为确定抖振响应的参考风速。结果为抖振位移和内力的RMS值(最大均方根或有效值)。塔1和塔2分别表示庆余向和遵义向桥塔。表8和表9分别为桥塔与梁体提取抖振响应代表位置的编号。
图7为桥塔裸塔施工状态、最大悬臂状态与成桥状态在0°攻角下的横桥向抖振位移RMS(均方根)值,由图表可知在最大悬臂施工状态塔顶截面有最大值约9 cm,且位移值方面,最大悬臂状态>裸塔状态>成桥状态。图8展示了为不同攻角下最大悬臂状态与成桥状态对应梁体的位移RMS值。
结果表明横向位移明显小于竖向位移,最大悬臂状态的最大竖向位移为+3°攻角下边跨1/2处的66 cm,成桥状态最大竖向位移为-3°攻角下主跨跨中62 cm。
2.5 施工与成桥状态抖振内力响应
图9为桥塔裸塔状态、最大悬臂状态与成桥状态在0°攻角的横桥向抖振内力RMS值,图线表明在最大悬臂施工状态塔底截面有最大值约1 035 231 kN·m,且内力值方面,最大悬臂状态>裸塔状态>成桥状态。图10分别为+3°攻角下最大悬臂状态与成桥状态对应梁体内力RMS值。+3°攻角工况下内力RMS值为最大,最大悬臂状态梁体最大内力为中跨1/4处梁截面,扭矩7 097.8 kN·m,竖向弯矩1 517.72 kN·m,橫桥向弯矩1 635.72 kN·m;成桥状态最大内力为塔1处梁截面,扭矩4 964.26 kN·m,竖向弯矩469.8 kN·m,横桥向弯矩353.66 kN·m。
3 结论
通过对本桥桥址处的风参数分析,主梁断面的气动参数分析和结构有限元计算以及抗风性能计算分析,得出结论:
(1)通过对湘江特大桥动力特性分析可以看出,结构基频相对较低,结构偏柔,但梁身扭转刚度较大,这种特性对提高桥梁抗风性较为有利。
(2)通过计算湘江特大桥不同阶段下桥塔与梁体的风致抖振响应发现:桥塔在最大悬臂状态有最大抖振内力与位移RMS值;梁体在最大悬臂状态+3°攻角工况下有最大响应,且在边跨1/2处有最大位移RMS值,在中跨1/4处截面有最大内力RMS值;梁体在成桥状态+3°攻角工况下有最大响应,且在主跨跨中有最大位移RMS值,在塔1处截面有最大内力RMS值。
(3)湘江特大桥具有良好的的抗风稳定性,结构具有良好的气动。计算给出了桥梁施工和成桥状态的抖振内力,可用于设计单位进行相关设计和计算。
(4)该桥利用计算流体力学软件进行了桥梁结构的气动力计算,利用数值编程的方法得到结构荷载时程,再通过有限元软件进行结构的风致响应分析。该方法可用于其他同类型桥梁的初期抗风计算中。
参考文献
[1] 李永乐,廖海黎,强士中.大跨度铁路斜拉桥非线性时域抖振分析[J].西南交通大学学报,2004,39(3):375-380.
[2] 丁幼亮,胡心一,张志强,等.考虑桥塔风效应的多塔斜拉桥抖振响应分析[J].工程力学,2014,31(10):77-84.
[3] 周海波.大跨度斜拉桥最大单悬臂施工阶段抖振响应分析 [D].成都:西南交通大学,2014.
[4] 刘高,林家浩,王秀伟.考虑全桥耦合的大跨斜拉桥抖振内力分析[J].大连理工大学学报,2003,43(4):479-483.
[5] 李永乐,周述华,强士中.大跨度桥梁三维脉动风场的模拟[J].土木工程学报,1998,31(3):72-79
[6] 王浩,李爱群,焦常科.桥塔风效应对大跨度悬索桥抖振响应的影响[J].振动与冲击,2010,29(8):103-106.
[7] 李永乐,廖海黎,强士中.桥梁抖振时域与频域分析的一致性研究[J].工程力学,2005,22(2):179-183.
[8] 韩兴,黄博,祝兵.基于谱分解法的自锚式悬索桥桥梁风致抖振计算分析[J].铁道标准设计,2017,61(9):82-86.
[9] 孙长亮.山区大跨斜拉桥桥塔抖振响应研究[D]成都:西南交通大学,2013.
[10] 张晋媛.大跨度斜拉桥线性抖振时域分析[D]. 成都:西南交通大学,2013.
[11] 苏成,何滔.崖门大桥施工阶段风致振动时域分析[J].桥梁建设,2003,33(1):69-73.
[12] 巩鹏飞.公铁两用刚桁梁斜拉桥风致抖振时域分析[D]成都:西南交通大学,2013.
[13] 谷红强. 大跨度公铁两用斜拉桥风致抖振时域分析及挡风屏影响研究[D]成都:西南交通大学,2012.
