多子群的共生非均匀高斯变异樽海鞘群算法

陈忠云 张达敏 辛梓芸

近年,元启发式算法作为一种有效的演化计算技术,已受到众多学者的重视.元启发式算法是指受到生物行为和物理现象的启发提出的一类算法,其核心思想是实现搜索过程中随机性行为和局部搜索的平衡.常用的元启发式算法包括粒子群算法(Particle swarm optimization,PSO)[1]、正弦余弦算法 (Sine cosine algorithm,SCA)[2]、蝴蝶优化算法(Butterfly optimization algorithm,BOA)[3]、飞蛾扑火优化算法 (Moth-flame optimization algorithm,MFO)[4]、大红斑蝶优化算法 (Monarch butterfly optimization,MBO)[5]、蚯蚓优化算法[6]、大象放牧优化 (Elephant herding optimization,EHO)[7]等.这些算法已成功应用于各种科学领域,如过程控制、生物医学信号处理、图像处理以及许多其他工程设计问题.

樽海鞘群算法 (Salp swarm algorithm,SSA)[8]提出的一种新型启发式智能算法.樽海鞘群算法相对于粒子群算法等其他算法,具有结构简单、参数少、容易实现等优点.虽然樽海鞘群算法在求解大部分优化问题具有优越性,但与其他群智能算法一样,仍然存在求解精度低和收敛速度慢等缺陷.文献[9]提出固定惯性权重,可以加快搜索过程中的收敛速度,并应用于特征选择问题.文献[10]把樽海鞘群算法和混沌理论结合提出混沌樽海鞘群算法,在解决特征提取问题时,能发现最优特征子集,最大程度地提高分类精度,最小化所选特征的数目.文献[11]提出采用子群规模调整,每个子种群的大小随着进化的过程而逐渐增加,有利于提高算法在初始阶段的探测能力和后期的开采能力.文献[12]在算法中加入共享机制,改进原始算法的随机追踪的位置更新公式,降低搜索盲目性,提高收敛速度.文献[13]提出非均匀变异演化算法,使个体能够跳出局部最优,以克服早熟现象.文献[14]通过高斯变异来增强蝙蝠算法种群的多样性.

为解决标准樽海鞘群算法存在的求解精度不高和收敛速度慢等问题,本文提出了一种多子群的共生非均匀高斯变异樽海鞘群算法 (Multi-subpopulation based symbiosis and non-uniform Gaussian mutation salp swarm algorithm,MSNSSA).根据适应度值大小,将种群分为领导者、追随者和链尾者三个子群.首先对领导者位置更新公式中参数c1进行分析,以更好平衡探索和开发能力;然后对追随者位置更新公式采用共生策略,增加与最优个体的交流,增强局部开发能力;最后链尾者更新使用非均匀高斯变异,增强种群多样性.通过求解14个典型测试函数和CEC 2014 测试函数的最优解,验证了改进算法MSNSSA 的有效性和鲁棒性.

1 樽海鞘群算法

在樽海鞘群算法[8]中,樽海鞘链由领导者和追随者两种类型的樽海鞘组成.领导者是位于樽海鞘链的最前面,而其他个体则为追随者的角色.随机初始化种群:

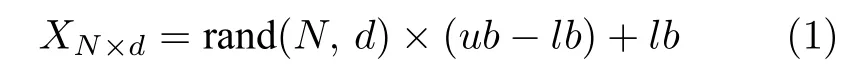
其中,N为樽海鞘群的规模,d为空间维数.

在SSA 中,食物源的位置是所有樽海鞘个体的目标位置,即探索过程中全局最优解,影响着领导者位置更新.领导者的位置更新公式如下所示:

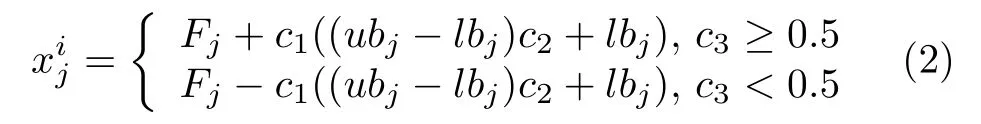
由式(2)可知,领导者位置更新主要受到食物源位置影响.其中参数c1定义如下:

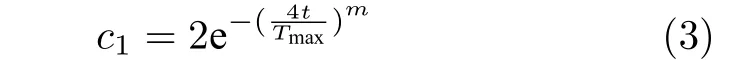
式中,t为当前迭代次数,Tmax为最大迭代次数,幂系数m=2[8].参数c1在迭代过程中自适应降低,当值较大时,有助于提升探索能力.而当值较小时,则有助于具体开发能力.系数c1可以使SSA 的探索能力和开发能力处于较好状态.因而系数c1是樽海鞘群算法中最重要的参数.

为更新追随者的位置,使用以下公式:

其中,由式(2)和式(5)可以模拟樽海鞘链的行为机制.

2 多子群的共生非均匀高斯变异樽海鞘算法

智能算法的核心是为了寻求探索能力和开发能力的平衡,为了实现这一点.本文在标准樽海鞘群算法基础上,以最小化问题为例,保持原种群个体数目不变的条件下,按照适应度值从小到大,均匀地把原有种群分为领导者、追随者和链尾者三个子群体.这三种子群体执行不同的更新策略,分别侧重于平衡搜索、局部搜索和全局搜索.并结合相应的进化策略,改善算法的优化性能.具体描述如下.

2.1 SSA 算法参数分析

领导者位置更新式(2)中,参数c1可以使SSA的探索能力和开发能力处于较好状态.因而系数c1是樽海鞘群算法中最重要的参数.式中的幂系数m的取值大小对算法探索能力和开发能力起到至关重要的作用.本文选取m从1.0 到3.5 之间分析对算法性能的影响.图1 为m取不同数值时,随迭代次数增加参数c1从2 递减到0 的变化曲线.

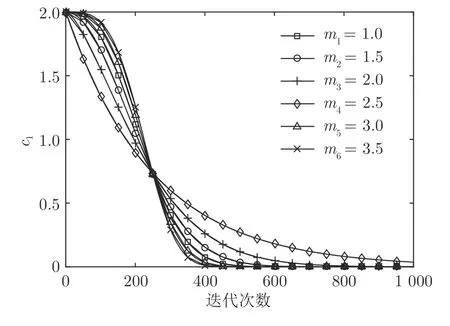
图1 c1 变化曲线Fig.1 c1 change curve

选取Schaffer 测试函数对参数进行分析,该函数在距全局最优点大约3.14 范围内存在无穷多个局部极小将其包围,并且函数强烈振荡.实验时,设定最大迭代次数为1 000,改变幂系数m后对Schaffer测试函数进行100 次寻优计算,则m对算法性能的影响如表1 所示.

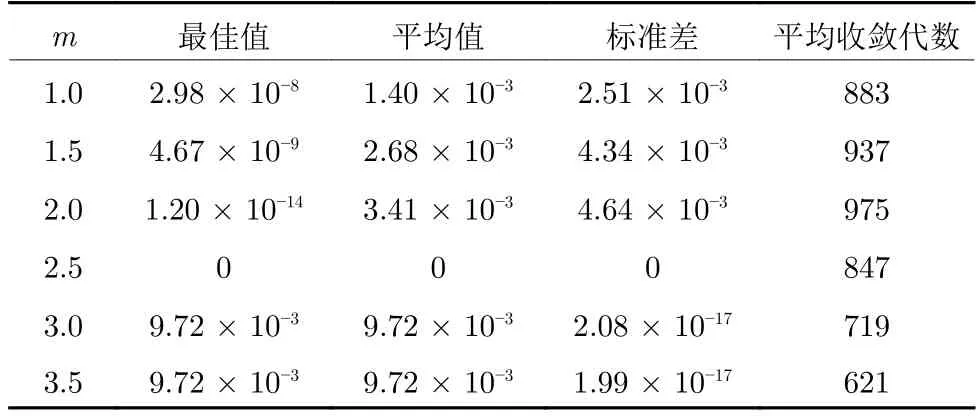
表1 参数m 对SSA 的影响Table 1 Influence of parameter m on SSA

如表1 所示,随着幂系数的增加,SSA 算法寻优的结果先增加后降低,当m=2.5 是寻优最优值达到0.无论是平均值和标准差,m=2.5 时都为最佳.随着m增加,平均收敛代数在降低.虽然此时m=2.5 的平均收敛代数没有m=3.0 和3.5 时的效果好,但是m=2.5 的寻优结果要比其余都要好.结合图1 分析可知,当m=2.5 时,迭代前期参数c1变化较快,能较好维持算法的全局搜索能力,迭代后期c1变化较慢,能有效提高算法的局部寻优能力,从而取得良好的寻优效果.综上可知,当m=2.5 时,参数c1能使SSA 算法的探索能力和开发能力处于更好的平衡状态.

2.2 共生策略

由式(5)追随者位置更新公式产生的新个体直接替换原个体,此更新方式存在以下缺点:1)更新后的追随者个体不管适应度值好与坏都直接替换原有个体,具有一定盲目性,会导致收敛速度降低;2)第i只樽海鞘位置会根据第i和i– 1 只樽海鞘位置进行更新,对先前个体依懒性较强,缺乏与其他个体学习的部分.若追随者的位置是局部最优解,则会容易陷入局部最优,出现停滞.为增强樽海鞘群算法的开发能力.本文提出一种共生策略对追随者位置进行更新,公式如下:

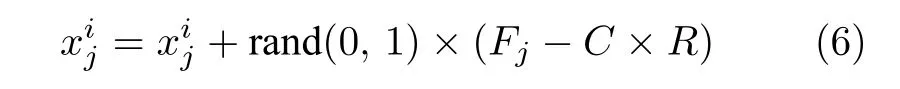
式中,rand(0,1)是(0,1)之间的随机数;Fj为食物源在第j维空间的位置;称为共生量,代表樽海鞘链中第i和i– 1 只樽海鞘的关系特征;R的作用解释如下:在自然界中,某些互惠关系可能给一个生物带来比另一个生物更大的有益优势.换句话说,樽海鞘i与樽海鞘i −1 相互作用时可能会获得巨大的利益.同时,樽海鞘i −1 与樽海鞘i相互作用时可能只会获得足够的利益或没有那么显着的利益.式中受益因子R是随机确定的1或2.这些因素代表樽海鞘个体是部分或全部受益于相互作用.经式(6)新产生的追随者需判断适应度值是否优劣后再替换原有个体.

在式(6)追随者位置更新策略中,增加了社会部分rand(0,1) × (Fj−C×R),使种群中的最优个体参与追随者的进化.与原来追随者更新式(5)只使用第i和i– 1 只樽海鞘位置进行信息交流的方式相比,社会部分引入更多组合模式,使其不再单一围绕前一个追随者附近搜索,即将追随者从原个体位置指引到食物源位置所在附近.从而提高算法的开发能力.

2.3 非均匀高斯变异

处于樽海鞘链尾端个体的适应度值较差,被分类为链尾者子群.对于这类樽海鞘个体可以很好地保留自身信息,而不是一味地朝着领导者移动.为增强种群多样性,本文为适应度值较差的链尾者提出一种非均匀高斯变异策略,其更新如下:

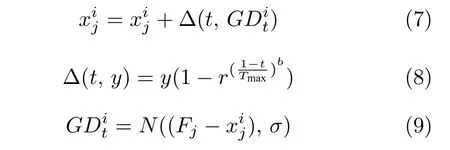
非均匀高斯变异策略有如下特色:1)其更新对象为种群中适应度最差的樽海鞘个体,而不是当前种群中的全部个体,降低变异计算复杂度.2)由式(7)可知,对链尾者更新公式以个体自身为基准,选择食物源位置与当前个体进行高斯分布后自适应调整变异步长的学习策略.该更新方式有利于保持种群多样性,进一步增强算法全局搜索能力.

综上所述,通过把原有算法种群分类为领导者、追随者和链尾者三个子群,分别对其执行不同的搜索任务.领导者子群负责平衡算法探索能力和开发能力.追随者子群负责增强算法开发能力.链尾者子群负责增强算法探索能力.进化过程中每一个子群有针对性地进行搜索,更适合自身的进化需求,增强算法求解性能.

3 仿真实验与结果分析

为验证本文提出的MSNSSA 在求解优化问题上的有效性和鲁棒性,将MSNSA 算法与加入共生策略的樽海鞘群算法 (记为SSSA)、加入非均匀高斯变异的樽海鞘算法 (记为NSSA)、SSA、PSO[1]、SCA[2]、BOA[3]和MFO[4]在14个典型的标准测试函数[15]最优值求解上独立进行50 次对比实验.

实验1.采用如表2 所示14个复杂函数作为适应度函数.选取的测试函数中包含单峰、多峰、可分和不可分等不同特征的测试函数.表2中测试函数维度从2 维到200 维,可以更加全面地验证算法性能.

表2 基准函数Table 2 Benchmark function

实验最大迭代次数为1 000,种群个数为30,各算法其余的参数设置如表3 所示:

表3 参数设置Table 3 Parameter settings

通过50 次独立试验后从每种算法获得结果的最佳值、平均值和标准偏差以及求解成功率SR%和平均耗时T等多个实验对比数据如表4 所示.其中求解成功率为计算成功次数除以本次实验的求解次数.判断一次求解是否成功按照下式:

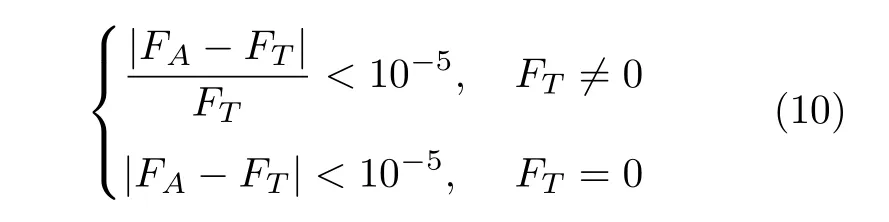
式中,FA为每次实际求解最佳值,FT为测试函数理论最佳值.

首先,对于表4 中的最优值、平均值都可以反应算法的收敛精度和寻优能力.对于6个单峰函数f1～f6,MSNSSA 在求解f5和f6函数时,寻优精度达到理论最优值0.同时,随着搜索空间维度的增加,寻优收敛精度f1至f4函数有所下降,因为伴随求解维度的增加,对于算法求解难度也呈指数级别递增,所以算法的收敛精度有所降低.随着维度增加SSA、SCA、MFO 算法求解精度较差,其中SCA 算法求解100 维的Rosenbrock 时与理论最优值存在1.0 × 107级的误差.对于只引入共生策略的SSSA 和引入非均匀高斯变异的NSSA 两种算法的寻优精度较和标准差都比原始SSA 要好,这说明引入不同策略可增强算法性能.而MSNSSA 相对与其他几种算法寻优精度和标准差都要好,且求解部分单峰函数达到理论最优值.对于8个多峰函数f7～f14,算法求解精度相对于单峰函数要低一些.同样,随着维度增加算法求解精度也有所降低.当维度增加到200 维时,SSA 算法与理论最优值存在1.0 × 102级的误差.MSNSSA 算法在求解8个多峰函数中,有5个都达到了理论最优值.在求解函数f7和f10时,包括MSNSSA 在内的其余4 种算法都达到了理论最优值,但MSNSSA 的平均值比其他几种算法都要好.在求解函数f8时,8 种算法都达到了理论最优值,但MSNSSA、SSSA 和NSSA三种算法的平均值比其他算法好.求解其他函数时,MSNSSA算法比其他算法的精度都较高.另外SSSA 和NSSA 比标准SSA 寻优结果基本较好,进一步说明加入不同策略对算法性能有所提升.可见MSNSSA算法在求解单峰、多峰、可分、不可分以及高维的基准函数时都有明显的优势.

其次,表4 中标准差和成功率可以反映算法的稳定性和跳出局部最优的能力.MSNSSA 算法独立50 次计算的都很接近理论最优值、标准差也较小.说明MSNSSA 的寻优求解有着一定的稳定性.另外,MSNSSA 算法标准差始终都要比另外几种算法要优秀,进一步验证了MSNSSA 的有效性.14个基准函数中有单峰、多峰、低维和高维,除了f4和f9函数,MSNSSA 在成功率基本上为100%,而标准SSA 在f1函数的成功率为100%以外,其余基准函数成功率几乎为0.随着搜索维度的增加,标准SSA 在寻优求解能力上表现出很大不足.特别是在求解多维函数时,最优值和成功率都很差,说明标准SSA 在跳出局部最优的能力较弱.而在MSNSSA和SSSA 中都引入共生策略,这对算法跳出局部搜索具有很大作用.

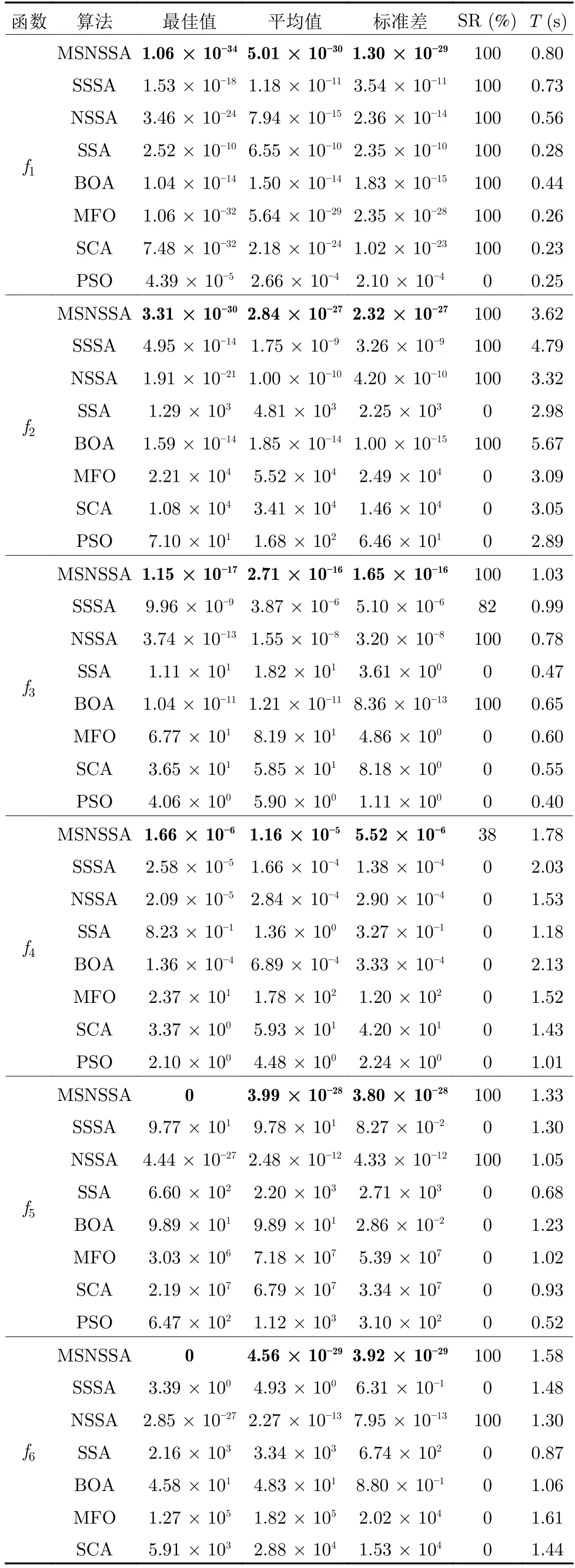
表4 基准函数结果对比Table 4 Comparison of benchmark function results

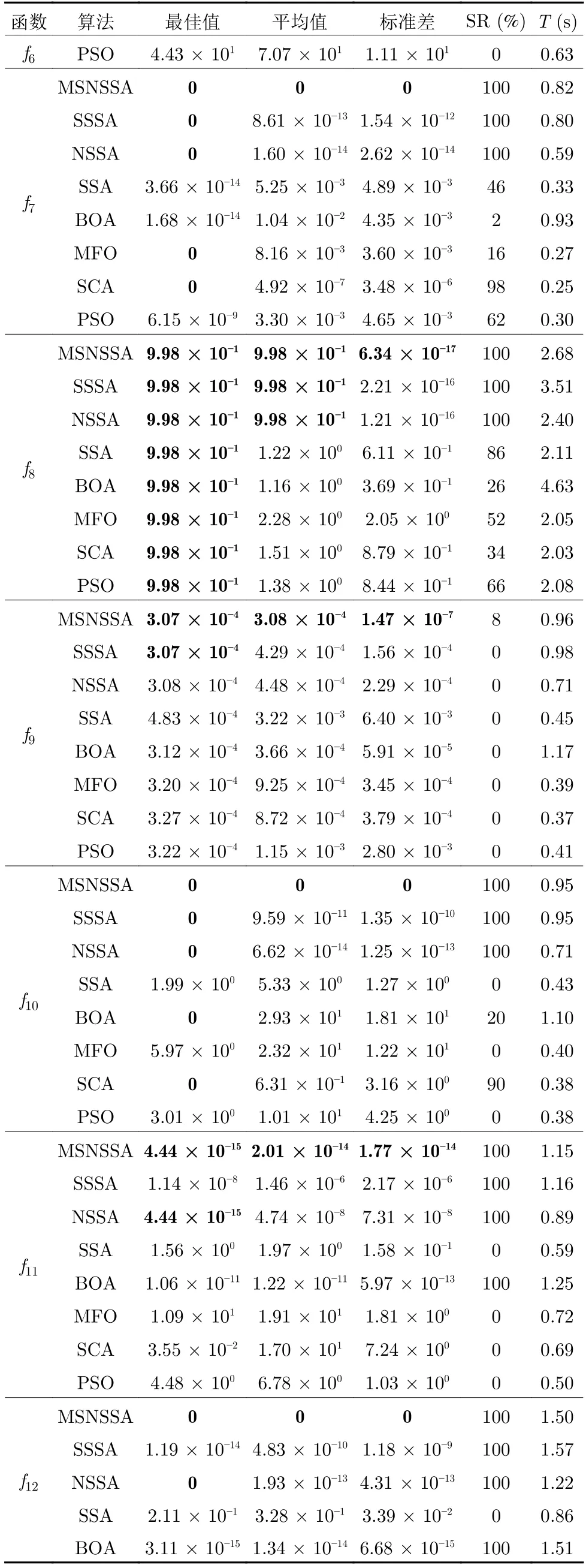
表4 基准函数结果对比 (续表)Table 4 Comparison of benchmark function results (continued table)

表4 基准函数结果对比 (续表)Table 4 Comparison of benchmark function results (continued table)

从平均耗时来看.由表4 可知,SCA 和PSO 平均耗时最短,改进的MSNSSA、SSSA、NSSA 这3种算法相对于标准SSA 的平均耗时都要大,此种情况也在合理范围内.因为算法中引入更多的算子,使得算法能够搜索到更多解,导致运行时间变长.总体来看,MSNSSA 平均耗时比另外两种算法增加的并不是很大,在允许范围内.

图2 给出6个基准函数的平均收敛曲线图,各函数分图图例同图2(f)一致.由于MSNSSA 收敛精度较高,为了便于观察收敛情况,本文对寻优适应度值(纵坐标)取以10 为底的对数.由图2可以看出,在迭代前期,MSNSSA 和SSSA 两个算法收敛曲线下降很快,这说明引入共生策略,增加种群局部探索能力,使得算法一开始收敛速度就较快.随着更迭次数的增加MSNSSA 算法持续寻优,在迭代后期也未出现停止状况,收敛速度比其他算法都要快,且寻优精度较高.另外,在迭代后期MSNSSA比只加入非均匀高斯变异的NSSA 收敛速度要快,说明非均匀高斯变异增强了种群多样,验证了改进算法的有效性.MSNSSA 在函数f7和f10上寻优精度达到理论最优值0.而标准SSA 算法收敛速度慢,前期和后期都出现不同程度的停滞.从图2 可知,其他算法在前期和后期都出现停滞现象.

无论单峰、多峰,还是低维和高维,对于每个函数MSNSSA 比另外7 种算法的收敛速度和寻优精度都要好.由表4 可知,对于函数f7和f10,MSNSSA的最佳值为0.所以在图2(d)和图2(e)中,MSNSSA曲线后面部分没有显示.

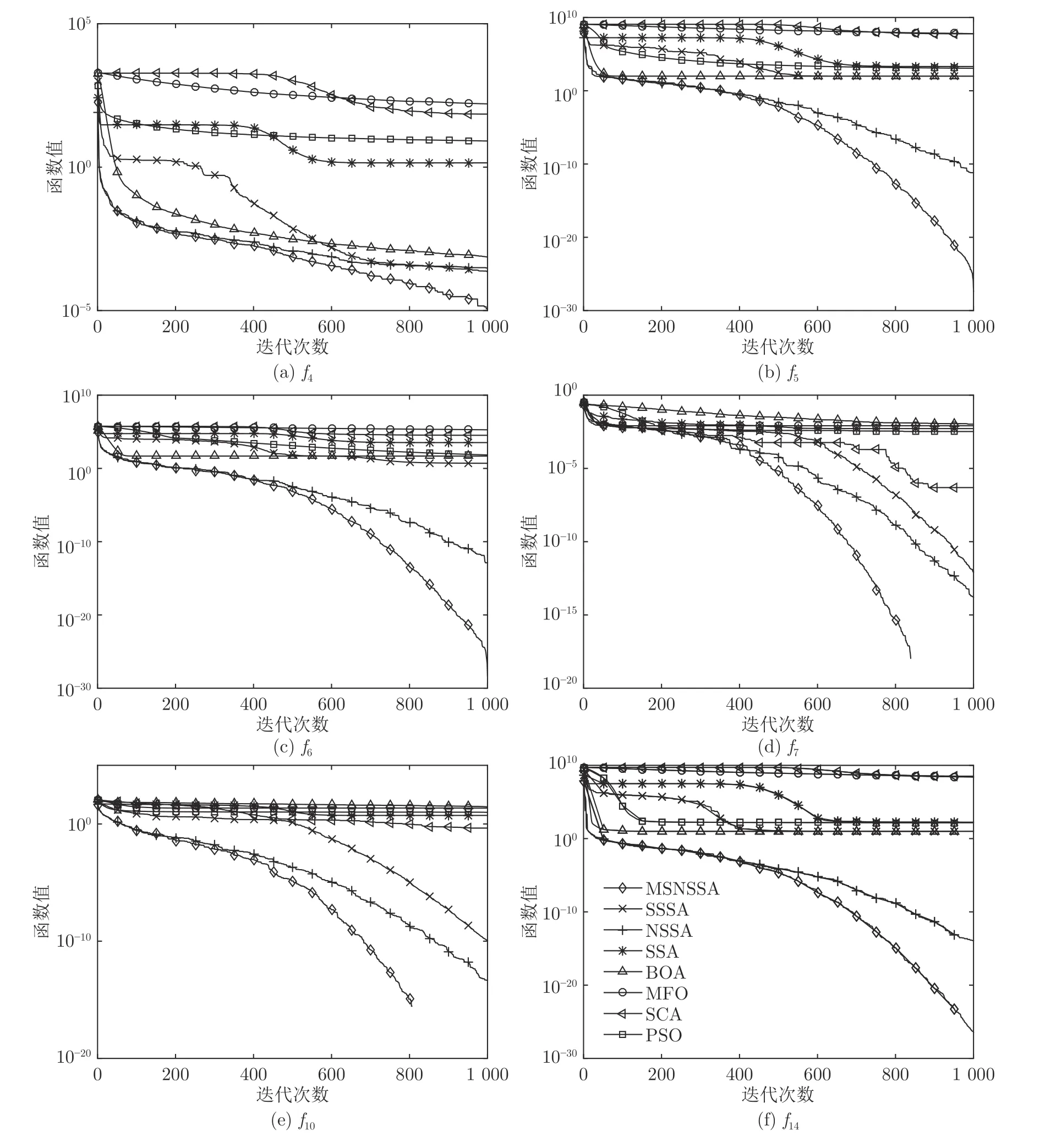
图2 基准函数平均收敛曲线Fig.2 Function average convergence curves

基于50 次独立运行算法的平均值和标准差二者之间不相互对比每次运行结果.文献[16]提出对于改进进化算法性能的评估,应该进行统计检验.换而言之,仅基于平均值和标准偏差值来比较算法还不够.需要进行统计检验以验证所提出的改进算法比其他现有算法具有显著的改进优势.为了判断MSNSSA 的每次结果是否统计上显著的与其他算法的最佳结果不同,采用Wilcoxon 秩和检验在5%的显著性水平下进行.表5 给出所有基准函数的MSNSSA 和其他算法的Wilcoxon 秩和检验中计算的p值.例如如果最佳算法是MSNSSA,则在MSNSSA 与SSSA,MSNSSA 与SSA 等之间进行成对比较.由于最佳算法无法与自身进行比较,因此,针对每个函数中的最佳算法标记为N/A,表示不适用.这意味着相应的算法可以在秩和检验中没有统计数据与自身进行比较.符号 “+”、“－”和“=”分别表示MSNSSA 的性能要优于、劣于和相当于对比算法.根据文献[16],当p<0.05 时,可以被认为是拒绝零假设的有力验证.

由表5 可知,MSNSSA 的p值基本小于0.05.只有在f7的MSNSSA 与SSA 时,p值大于0.05.这表明该算法的优越性在统计上是显著的.即MSNSSA 算法比其他算法具有更高的收敛精度.

表5 基准函数Wilcoxon 秩和检验的p 值Table 5 p-value for Wilcoxon＇s rank-sum test on benchmark function

所有算法的定量分析是基于14个基准函数的平均绝对误差 (Mean absolute error,MAE).文献[17]提出对优化算法进行排序,MAE是一种有效且可行的性能指标.表6 给出了这些基准函数的MAE排序,计算公式如下:

式中,mi为算法产生的最优结果的平均值,oi为相应基准函数的理论最优值,Nf为基准函数个数.计算值见表6.

由表6 可知,MSNSSA 算法排名为1.与另外7 种算法相比,MSNSSA 算法提供最小的MAE,进一步说明MSNSSA 算法的有效性.NSSA 和SSSA分别排第2 名和第3 名.

表6 MAE 算法排名Table 6 MAE algorithm ranking

实验2.为更好评估MSNSSA 的有效性和稳定性.本文还在CEC 2014 基准函数中选取部分单峰、多峰、混合和复合类型的函数进行优化求解,如表7所示.实验种群规模为30,最大迭代次数为1 000,维度为30.

表7 CEC 2014 基准函数Table 7 CEC 2014 benchmark function

表8 记录了CEC 2014 中部分函数独立运行30 次后每种算法的平均值和标准差的结果.CEC 2014 函数具有复杂的特征,因此所有算法都较难找到函数最优值.根据表8 中结果显示,MSNSSA 在6个基准函数上都求得比其他5个算法更优的结果.验证MSNSSA 具有较好的有效性和鲁棒性.

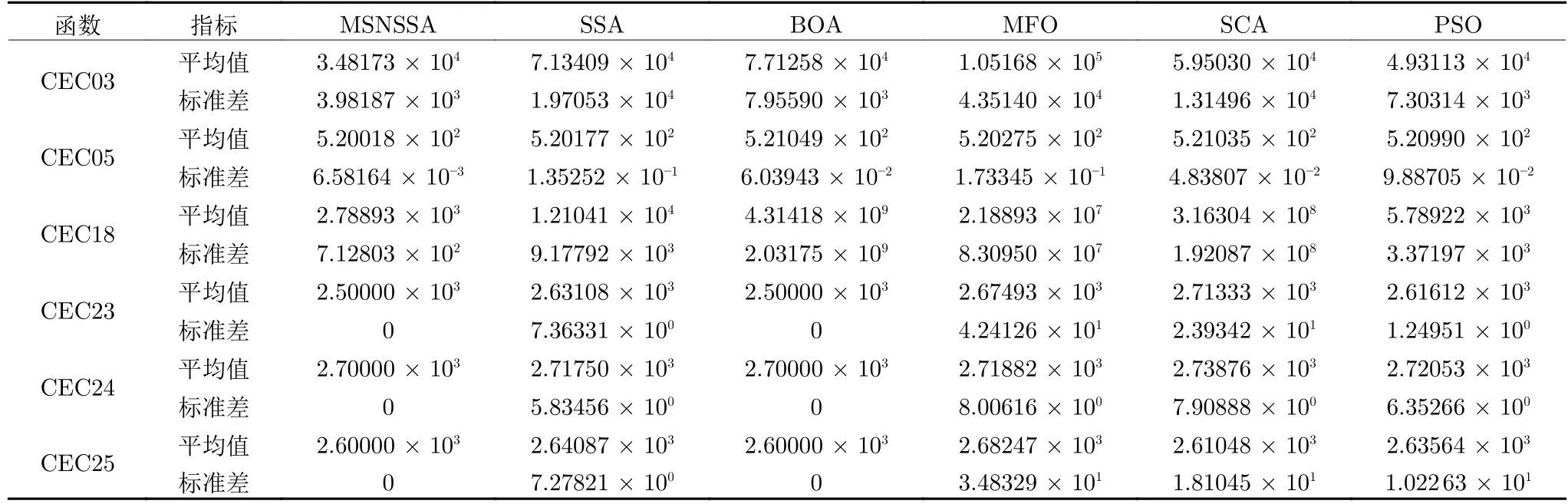
表8 CEC 2014 优化结果对比Table 8 Comparison of optimization results of CEC 2014

为比较本文的多子群MSNSSA 算法与其他多子群算法和改进樽海鞘群算法的优劣.其中,MFOASQP (Multiple subgroups fruit fly optimization algorithm based on sequential quadratic programming local search)[18]是基于局部搜索的多子群果蝇优化算法,鸡群算法 (Chicken swarm optimization,CSO)[19]是一种新型的天然多种群优化算法,HCPSO (Improved particle swarm optimization based on hierarchical autonomous learning)[20]是基于分层自主学习的改进粒子群优化算法,DMSPSO (Dynamic multi-Swarm PSO)[21]是动态多子群粒子群优化算法,PSO-SMS (Self-adaptive multi-swarm PSO)[11]是自适应多子群粒子群优化算法,CASSA (Crazy and adaptive salp swarm algorithm)[22]是疯狂自适应的樽海鞘群算法,CESSA (Chaotic and elite centroid stretching mechanism salp swarm algorithm)[23]是混沌精英质心拉伸机制樽海鞘群算法,ICMOABC (Interval cooperative multi-objective artificial bee colony algorithm)[24]是区间合作多目标人工蜂群算法,HCMOIWO (Hybrid cooperative multi-objective optimization invasive weed optimization)[25]是混合合作多目标优化入侵杂草优化,MPEA(Multi-population evolutionary algorithm)[26]多子群进化算法.各算法在种群数量为50,搜索维度为30 维,迭代次数为2 000 的情况下,将本文改进算法独立运行50 次后与其他参考文献的几种多子群算法和改进樽海鞘群算法进行对比,引用文献[18]和文献[20]的数据见表9 和表10.

由表9 和表10 可知,在求解f1和f2函数时,MSNSSA 未达到最优,而求解其余几个函数在平均值和标准差较其余几种算法都能达到最优.因此,更进一步说明本文提出的MSNSSA 算法比其他多子群算法具有更大优越性.

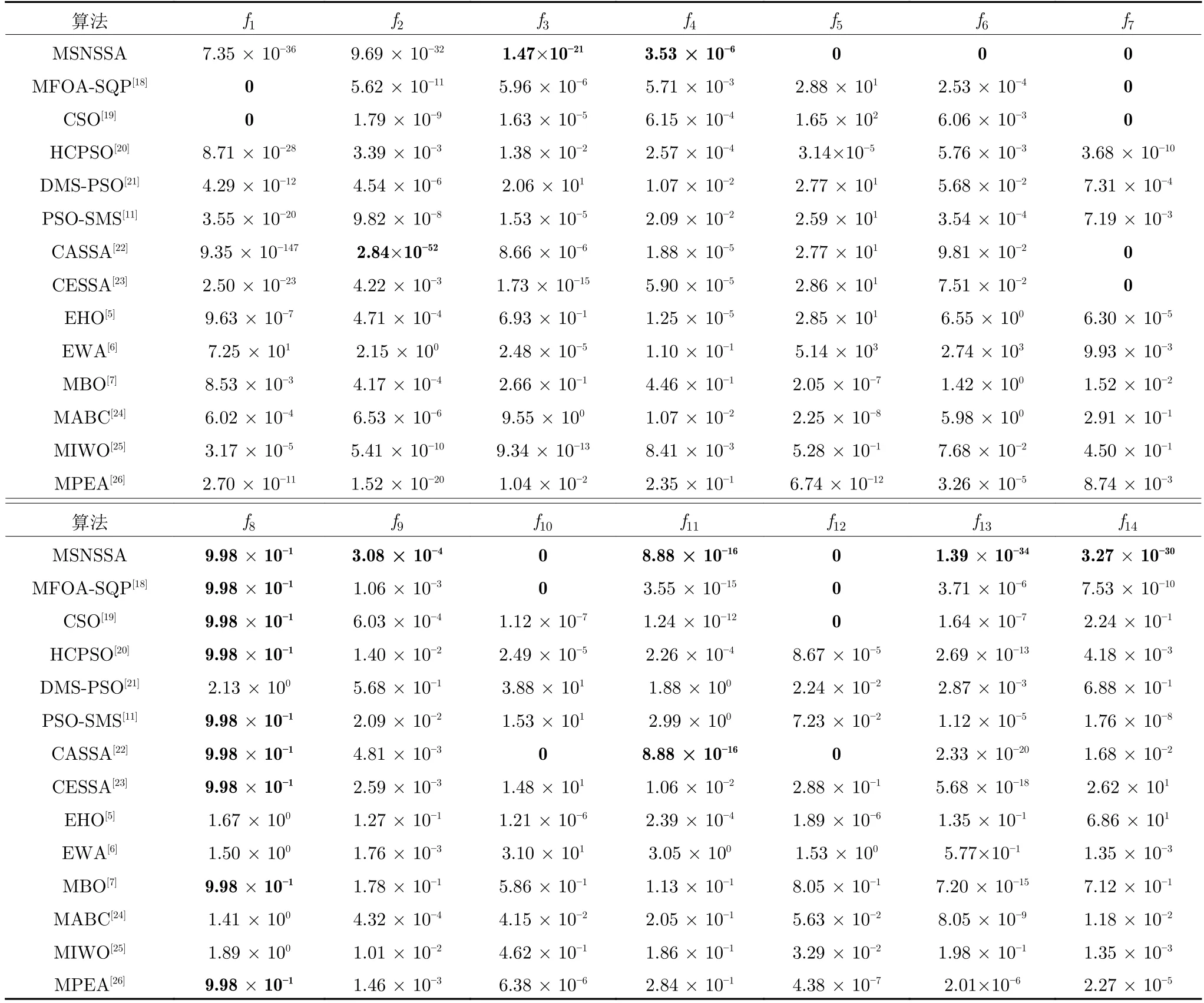
表9 与参考文献中算法均值的对比Table 9 Comparison of the mean with algorithm in references

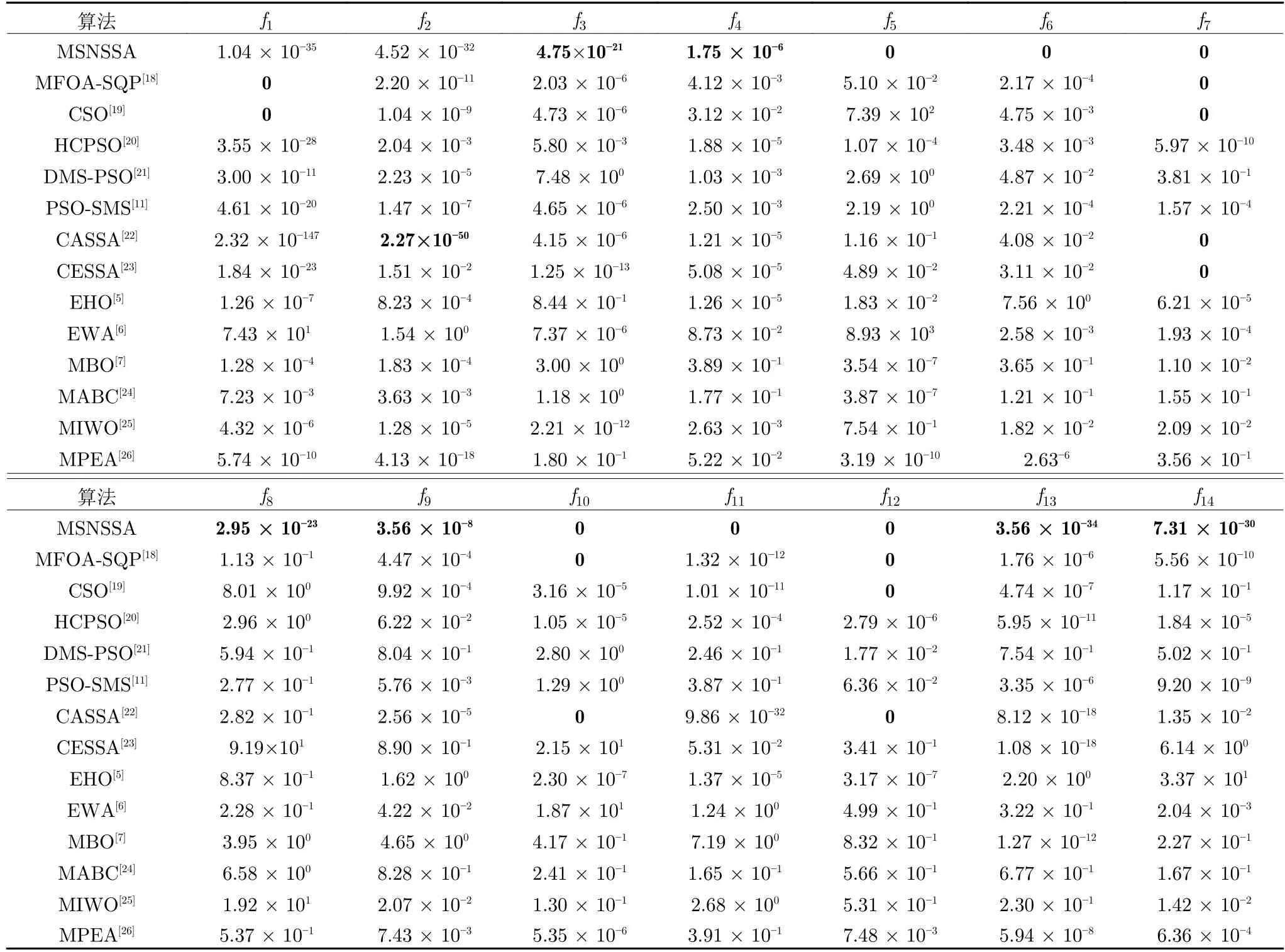
表10 与参考文献中算法标准差的对比Table 10 Comparison of the standard deviation with algorithms in reference

综上可知,多子群的共生非均匀高斯变异樽海鞘群算法对于本文多种基准函数都有很好的寻优结果.特别是对于高维、多峰的函数,具有较好的稳定性和寻优能力.

4 结束语

本文在标准樽海鞘群算法的基础上,分析领导者位置更新公式中的幂系数以平衡探索能力和开发能力,共生策略增强局部探索能力,非均匀高斯变异增加种群多样性,提出一种改进的多子群的共生非均匀高斯变异樽海鞘群算法.并将樽海鞘群算法应用于经典和CEC 2014 基准函数的寻优问题中.不仅使用最优值、标准差等指标对算法进行检验,本文还提出使用Wilcoxon 秩和检验对算法显著性水平进行验证.研究表明:多子群的共生非均匀高斯变异樽海鞘群算法可以获得更好的全局搜索和局部搜索能力,且收敛到质量更好的最优解,算法的有效性和鲁棒性也得到验证.在后续的研究中,考虑将改进的樽海鞘群算法应用到工程实践问题中,以进一步验证算法的性能.