金刚石氮-空位色心单电子自旋的电场驱动相干控制*

吴建冬 程智 叶翔宇 李兆凯 王鹏飞 田长麟 陈宏伟

1) (安徽大学物质科学与信息技术研究院,合肥 230601)

2) (中国科学院合肥物质科学研究院,强磁场科学中心,合肥 230031)

3) (中国科学技术大学物理学院,合肥 230026)

4) (中国科学技术大学附属第一医院,合肥 230001)

5) (中国科学技术大学生命科学与医学部,合肥 230026)

1 引言

氮-空位(NV)色心是金刚石中一种特殊的发光点缺陷.如图1(a)所示,当金刚石晶格中相邻的两个C 原子中的一个C 原子被N 原子所替代,另一个C 原子缺失形成空位时,就形成了氮-空位色心,即NV 色心.NV 色心的电子自旋基态是一种自旋三重态系统,使用光探测磁共振(optically detected magnetic resonance,ODMR)技术[1],即通过光学共聚焦系统可对单个NV 色心进行纳米级位置定位、量子态的初始化和读出[2],结合磁共振技术方法,可实现对NV 色心自旋量子态快速而精确地控制[3].NV 色心在室温条件下具有极佳的量子相干时间[4]和光学稳定性,可实现高保真度的量子逻辑门[5].作为量子比特应用于常温固态量子

图1 (a) NV 色心结构图;(b) 存在轴向磁场 Bz 下NV 色心的基态能级图,|↑〉 和 |↓〉 代表 15N 核自旋朝向;黄色和蓝色箭头分别代表Δms=±1跃迁和Δms=±2跃迁Fig.1.(a) Structure diagram of the NV center;(b) energy level diagram for the NV ground-state spin in the presence of an axial magnetic field Bz,|↑〉 and |↓〉 represent the spin orientation of 15N ;Δms=±1 transitions (yellow arrows) and the Δms=±2transition (blue arrows) are indicated.

‡ 通信作者.E-mail:hwchen@hmfl.ac.cn计算系统的搭建[6,7];也可作为纳米尺寸的量子传感器[8],用于磁场[9-12]、电场[13-19]、应力[20]、温度[21-24]等物理量以及单核自旋[25]等微小粒子的量子精密测量.精确地调控自旋作为关键技术,其每一次的发展都推动了NV 色心在量子计算、量子精密测量等领域应用的发展.

NV 色心中常用的自旋控制方法是基于由共振的交变磁场所实现的磁控制.但近年来利用交变电场与自旋形成电共振来实现电场控制自旋的相关研究,引起了研究人员的高度关注.Nowack 等[26]利用局域栅极产生的振荡电场,在量子点体系中实现了对电子自旋的电控制;Klimov等[27]对SiC半导体材料中点缺陷的电子自旋实现了电场相干控制;Asaad 等[28]在硅(Si)中对单个锑(123Sb)核自旋实现了电场相干控制等.自旋的电场控制相比传统的磁场控制的方法有一些显著的优点,如构建磁场所需的大线圈和强电流有可能影响其他设备,且磁场难以被局部化或屏蔽,很难实现单个自旋的寻址.而电场通过微型电极的尖端就能产生,且影响范围较小,这使得控制纳米尺寸的电子设备中的单个原子变得更加容易.本文通过加工于NV色心表面的电极所产生的可控交变电场,实现了对近表面NV 色心电子自旋的电控制.在实验上不仅观测到自旋在电场驱动下在|ms=-1〉与|ms=+1〉两个能级间的Rabi 振荡,还进一步研究了电场参数与Rabi 振荡频率间的关系.这种方法称为电驱动光探测磁共振(electrically driven optically detected magnetic resonance,EODMR)[27],电场驱动自旋所展现的Rabi 振荡称为ERabi.对于NV 色心电子自旋的电调控技术的研究与应用发展,有助于NV 色心与半导体芯片、自旋电子学器件等量子器件的结合[29],推动NV 色心量子体系在固态量子计算机、量子传感器等领域研究与应用的发展.

2 实验部分

2.1 实验原理

金刚石NV 色心具有C3v对称性,对称轴为由氮和空穴形成的晶轴方向,通常称为NV 轴.NV色心的基态为电子自旋三重态3A2,其3 个能级分别是|ms=0〉和|ms=±1〉,为表述方便,后文分别用|0〉和|±1〉来表示.在零场时|±1〉态能级简并,且与|0〉态能级之间有大小为D(约 2.87 GHz)的零场劈裂[30].如图1(b)所示,在外加磁场下,原本简并的|±1〉态能级会发生塞曼劈裂,|±1〉态之间的能级差变为 2γeBz,其中γe=28.03 GHz·T-1为电子自旋旋磁比[30],Bz表示沿NV 轴的磁场分量.NV 色心基态哈密顿量可表示为[31]

其中,d//=(0.35±0.02)Hz/(V·cm-1)和d⊥=(17±3)Hz/(V·cm-1)是NV 色心轴向和横向的电偶极矩[32],Si(i=x,y,z) 是自旋S=1 自旋算符.沿NV轴的电场(Ez)仅能改变自旋的能级大小从而引起共振频率的偏移,并不能直接驱动不同量子态之间的跃迁,并且d//相较于d⊥小了1 个量级,因此主要考虑垂直于NV 轴的横向电场E⊥(Ex(y))的作用.电场驱动自旋共振与常规的磁场驱动自旋共振的形式类似,区别在于它耦合了不同的自旋本征态对.横向驱动电场和磁场的哈密顿量可以分别写成:

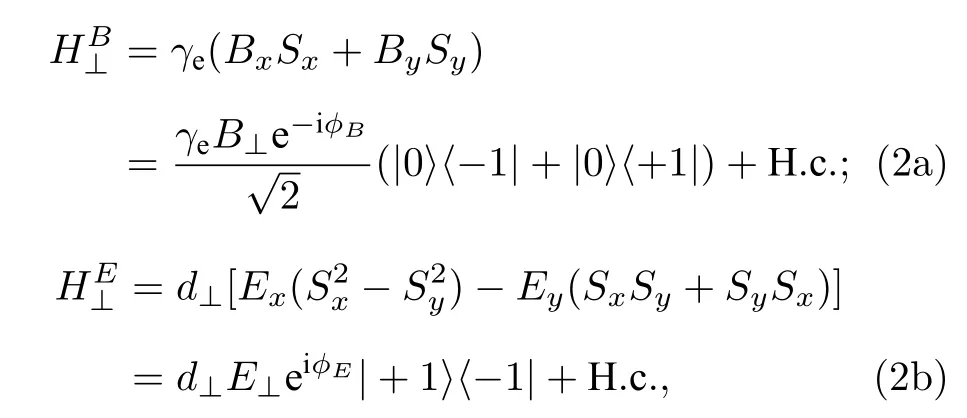
式中B⊥(E⊥)和ϕB(E)分别是横向平面内的磁(电)场的幅度和相位,H.c.表示厄米共轭.由(2a)式可以直观看出,常用的磁场调控方法是通过施加横向的共振脉冲磁场来激发电子自旋,从而实现从|0〉态到|-1〉态或|+1〉态之间的跃迁(Δms=±1).但是|-1〉态到|+1〉态之间,由于选择定则条件的约束,Δms=±2 能级之间的直接跃迁是磁禁戒的,需要通过|0〉态作为中间态而间接实现.这不但增加了操作的复杂度,也会引入额外的误差.(2b)式的哈密顿量表明,横向的共振交流电场理论上可以直接驱动NV 色心自旋的|-1〉态到|+1〉态之间的跃迁,这弥补了磁控制方法的不足.将利用磁场驱动自旋|0〉态到|±1〉态之间的跃迁以及利用电场驱动自旋|-1〉态到|+1〉态之间的跃迁方法相结合,可以实现对NV 色心3 个自旋能级之间直接跃迁的全操控.

2.2 实验装置

实验中选用的金刚石样品由化学气相沉积(chemical vapor deposition,CVD)生长而成,并经过2.5 keV 的15N 离子注入和99.999%的12C 纯化,最终切割成2.0 mm×2.0 mm×0.5 mm 的块材.在此离子注入能量下产生的NV 色心距金刚石表面约5 nm,可以更好地与外加电场耦合.生长金刚石所用的原料进行了12C 纯化,使金刚石表面的NV 色心自旋也具有毫秒级以上的量子相干时间(图3(b)).我们将电极与微波信号源组成回路,通过微波信号源在电极两端施加交变电压,电极上就会产生并向周围辐射交变的电磁场,其频率与微波信号源的频率相同.由于NV 色心自旋与电场和磁场共振的频率不同,将两个微波信号源分别与两组电极相连,其输出频率分别设定在电场和磁场不同的共振频率上,就可以分别实现其与NV 自旋的电场共振或磁场共振.具体而言,为了实现电控制,我们在金刚石表面镀了一对金电极,电极的结构如图2(a)所示.电极厚度约为百纳米,电极间的距离约为 10µm .从电极上接出两根导线与微波信号源(MWE)相连,其产生的交变电压施加在这对电极两端,在这对电极中间产生交变电磁场.将 M WE的频率设定在电场共振频率,利用该频率下的电场与NV 色心自旋共振,实现对NV 色心自旋的电控制.同时在距离电极 10µm 处镀了一根金线作与微波信号源(M WB)相连,将 M WB的频率设定在磁场共振频率,利用流经金线的交变电流所产生的交变磁场实现实验所需的辅助磁控制.金刚石样品放置于基于ODMR 技术搭建的实验平台上.图2(b)是激光共聚焦扫描NV 色心的荧光图,电极中间是待操控的NV 色心电子自旋.金刚石色心受到特定波长的激光激发后会发出荧光,其荧光的强度(IPL)与自旋所处能级相关.NV 色心自旋处于|0〉态时发出的荧光较强,被称为亮态;而处于|±1〉态时发出的荧光弱,被称为暗态.我们首先通过激光极化将NV 色心自旋初始化至|0〉态上,然后通过观测NV 色心自旋在磁驱动或电驱动脉冲序列操控后的末态的荧光强度的变化,得到NV色心自旋量子态的变化,从而实现对自旋跃迁过程的观测.

图2 (a)电极和微波线的结构设计简图;(b) 激光共聚焦扫描NV 色心的荧光图Fig.2.(a) Structural design diagram of electrode and microwave line;(b) fluorescence diagram of NV centers scanned by a laser scanning confocal microscope.

2.3 实 验

图2(b)为激光共聚焦扫描NV 色心的荧光图,其中孤立的亮点即是单个NV 色心,实验中所使用的NV 色心由白圈标出,其周围较暗的背景荧光是由激光长时间猝灭造成的.在通过激光共聚焦扫描NV 色心的荧光图定位到待操控的NV色心后,我们基于ODMR 的序列扫描微波频率得到ODMR 频率谱,见图3(a).在零磁场条件下,|±1〉态能级简并,在频率等于零场分裂能D=2870 MHz处会有一个共振峰,代表|0〉到|±1〉态能级的跃迁.当施加沿NV 轴的外磁场Bz时,由于塞曼效应,共振峰会分裂为2 个,对应的频率为D±γeBz.由于该NV 色心电子自旋有一个近邻的自旋为 1/2 的15N 核自旋,受到核自旋与电子自旋的耦合作用,根据15N 核自旋的方向不同,每个共振峰各自又会分裂为2 个.最终在频率扫描谱上,零场共振峰频率两侧的对称位置会出现2组共4 个共振峰,频率分别为D-γeBz ±A/2 和D+γeBz ±A/2,其中A的值为3.05 MHz,是15N核自旋与NV 色心的电子自旋的耦合常数[33].同样受到15N 核自旋的影响,|-1〉态到|+1〉态间的跃迁会有两个共振频率(2γeBz ±A).如图3(a)所示,红线是用洛伦兹函数进行的数据拟合,通过ODMR 频率谱共振峰的位置解析计算,可以得到轴向磁场Bz为181.47 G (1 G=10—4T),并且可以估算出|-1〉态到|+1〉态的两个跃迁频率分别为1013.25 MHz 和1019.32 MHz.

图3 (a) ODMR 的频率谱;(b) NV 色心电子自旋的相干时间测量.12C 纯化延长了电子自旋的相干时间,弛豫时间 T2 经指数衰减函数 e xp[-(2τ/T2)2] (红线)拟合约为1.6 msFig.3.(a) The frequency spectrum of ODMR;(b) coherent time measurement of electron spin in NV center.The purification of 12C prolongs the coherence time of electron spin,and the relaxation time T2 is estimated to be 1.6 ms through the exponential attenuation function e xp[-(2τ/T2)2] (red line).

要实现电场驱动控制,电场的频率需要满足共振条件.EODMR 的自旋跃迁过程如图4(a)所示.首先利用532 nm 的激光将NV 色心自旋初始化至|0〉态,通过横向的共振交变磁场驱动 πMW脉冲将自旋转至|-1〉态,随后施加一定时间的电场脉冲PE,上文已经通过ODMR 谱估计了|-1〉态到|+1〉态之间跃迁对应的频率,保持电场作用的时间和功率不变,在预估的跃迁频率附近进行扫频.当电场的频率达到共振频率时,共振的电场就会驱动NV 色心电子自旋|-1〉态的布居度向|+1〉态迁移.这将导致在随后读出过程中,用微波将|-1〉态转回|0〉态的布居度会小于非共振电场时的布居度,使观测得到的荧光计数降低.对测量的荧光计数使用洛伦兹函数进行拟合,如图4(b)所示,在荧光谱频率为1019.3 MHz 处观测到一个共振信号峰,结合前面的推导分析,此信号峰是15N 核自旋向下时,电场频率与NV 色心电子自旋发生共振,驱动电子自旋在|-1〉态到|+1〉态之间跃迁而产生的共振信号峰,通过读取谱图中信号峰的位置可以得到准确的电场共振频率.此时施加的电场功率为0.28 W,外磁场Bz为181.47 G.

图4 (a) EODMR 脉冲序列及自旋跃迁示意图;(b) EODMR 的共振峰谱图Fig.4.(a) EODMR pulse sequence and spin transition diagram;(b) the resonance peak spectrum of EODMR.

通过扫描电场得到准确的电场共振频率后,将产生的交变电场频率固定为共振频率1019.3 MHz,保持电场的功率不变,并不断增加电场脉冲PE作用的时间,脉冲序列如图5(a)所示.在荧光谱中可以清晰地观测到荧光计数随驱动时间的周期性变化,这种周期性振荡信号即为电驱动下电子自旋的Rabi 振荡.这是由于电场驱动NV自旋在|-1〉态与|+1〉态之间跃迁,使得|-1〉态的布居度周期性改变,最终导致转回到|0〉态的布居度也发生周期性改变.图5(b)中3 条ERabi振荡曲线分别对应于功率为0.28,0.20,0.14 W的电场驱动,红线是使用正弦衰减函数进行的数据拟合.可以直观地发现ERabi 振荡的频率受到驱动电场的功率调制,电场驱动功率越大,ERabi 振荡越快.电场源功率为0.28 W 时,πE脉冲的时间约为 6.65µs,在目前相干时间约为 1.6 ms 的情形下,可对NV 色心进行数百个量子逻辑门操控.

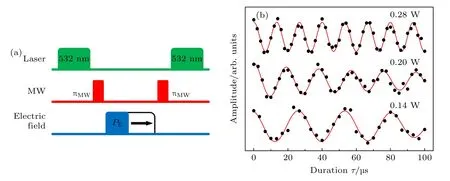
图5 (a) ERabi 脉冲序列;(b) 在不同电场驱动功率的作用下,NV 色心电子自旋的ERabi 振荡谱Fig.5.(a) ERabi pulse sequence;(b) ERabi oscillatory spectrum of electron spin in NV center under the action of different electric field driving power.

为了进一步找到ERabi 振荡频率与驱动电场的频率、功率等参数之间的关系,我们观测在不同共振频率下电场功率与电子自旋的ERabi 振荡的频率的关系.实验测量了频率从0.2,0.4,0.8 至1 GHz 下,不同功率的电场驱动ERabi振荡的频率.从图6 中可以清楚地看到,ERabi 的振荡频率与驱动电场频率无直接关系,与驱动电场功率开方(即驱动电场场强)成线性正相关,ERabi振荡频率与电场源功率W的开方的拟合函数关系为:实验结果也进一步表明观测到的ERabi 振荡是由电场驱动,通过电场对金刚石NV 色心电子自旋实现精密操控是完全可行的.通过增加驱动电场功率,从而加大电极间的电压可以提高自旋的操控速度,以减少量子逻辑门的操作时间.但目前由于电极之间的介质为空气,其击穿电压约为30 kV/cm.为了避免电极被击穿,电极电压无法加得很高,电驱动速率较慢.在后续研究中可通过微纳加工将电极置入金刚石内,金刚石的击穿电压约为21.5 MV/cm[34],可以极大提高控制电场的功率上限,理论预计可提计2—3个数量级,达到与磁控制相近的控制能力.

图6 不同共振频率下电场功率与电子自旋的 ERabi 振荡频率的关系Fig.6.Relationship between electric field power and ERabi oscillation frequency of electron spins at different resonance frequencies.

3 结论

目前电场对量子自旋进行操控的研究十分重要且具有广阔的应用前景.本文通过施加交变电场实现了对NV 色心自旋的电场调控,观测到在共振电场的驱动下NV 电子自旋在|-1〉态与|+1〉态之间 Δms=±2 的直接跃迁,并探究了电场功率与操控速率的线性关系.研究结果表明利用共振的电场与共振的磁场一样可以实现对量子自旋的快速精准的操控.在金刚石NV 色心量子体系中引入电场调控方法,将电控制与磁控制技术方法相结合,能够实现对NV 色心三个自旋能级间直接跃迁的全操控.自旋电调控技术的深入研究,有助于NV色心与半导体芯片、自旋电子学器件等量子器件的结合[29],进一步推动NV 色心量子体系在固态量子计算、量子传感等领域研究与应用的发展.