高能带电粒子束对陡峭密度梯度区照相的散射效应解析模型

李亮亮 王晓方

(中国科学技术大学物理学院,合肥 230026)

1 引言

惯性约束核聚变采用激光直接驱动或激光转换的X 射线间接驱动,内爆向心压缩靶丸实现热核聚变,而靶丸通常是由包含烧蚀层和聚变燃料等不同材料构成的多层球形靶[1,2].在多层球靶的不同材料界面以及在烧蚀区和激波前沿,都会出现陡峭密度梯度区.这些区域的存在不仅影响流体力学不稳定性增长,例如烧蚀型瑞利-泰勒不稳定性,也影响能量输运过程.这些界面或密度梯度区的宽度在1 µm量级甚至更小,实验研究中为了能够诊断出它们,需要高分辨的诊断手段.由于密度梯度区的物质稠密,通常采用X 射线照相进行诊断.受X 射线成像系统分辨能力以及X 射线脉冲时间宽度致模糊效应所限,迄今实验中获得的最好分辨能力接近2 µm[3-5],尚难以诊断1 µm 甚至更窄的陡峭密度梯度区.

近年来超短超强激光产生带电粒子(质子、电子等)束的研究取得快速进展,可以产生源尺寸小、脉冲时间短、亮度高的高能带电粒子束.其中,质子束的最大动能接近100 MeV[6],电子束的最大动能已达到8 GeV[7].带电粒子束基于其在电磁场中偏转,已应用于放射照相诊断等离子体的电磁场[8,9];基于在靶物质中能量损失,已应用于诊断面密度和不均匀性[10-12].带电粒子和靶物质相互作用的物理性质表明,对于放射照相,当靶物质厚度和带电粒子的射程接近时,带电粒子的能量损失或被靶物质吸收才比较显著.当带电粒子的动能很大,即带电粒子的射程远大于靶物质厚度时,带电粒子的能损可以忽略[13-15].这种情况下,带电粒子束在靶物质中传输,主要发生库仑相互作用导致的弹性小角度散射,即带电粒子在靶物质中传输路径近似为直线,透射束的发散角与靶物质的面密度有关[16,17].近年的研究表明,当高能带电粒子束穿过具有横向陡峭密度梯度的靶时,陡峭密度区对高能带电粒子束的散射能直接反映在探测面上,即在接收的透射束通量密度分布中出现调制现象[10,13-15].陡峭密度梯度区的散射效应产生的这一调制现象对带电粒子束的能量发散不敏感,而且,密度梯度区越陡,这一现象越显著.因此,利用这一局域散射效应,有可能诊断陡峭密度梯度区[18,19].

目前对带电粒子束照相及散射效应的理论研究主要采用蒙特卡罗方法进行数值计算[10,13-15,18-20],已有供用户免费使用的蒙卡程序包，例如Fluka[21].不过,蒙卡计算很耗费计算机时,例如本文讨论的多层球靶,一个算例的计算需要机时超过60 h.为了和实验结果进行对比,还需要改变参数条件进行多个甚至大量算例的数值计算.其次,Fluka[21]的使用对输入参数设置范围有一定限制,例如常用的PS 材料(碳和氢的聚合物,化学成分CH)的密度最大值只能到 10 g/cm3,不适用于惯性约束聚变或高压下更高密度情况.因此,寻找更快速、有效的理论方法研究高能带电粒子束照相及散射效应十分重要.

根据带电粒子在靶物质中散射的性质,本文发展了一个分析高能带电粒子束照相散射效应的解析模型.使用该模型对密度梯度靶和多层球靶照相的计算结果与Fluka 模拟结果进行了比较,以确认该模型的可靠性.在此基础上,应用该模型分析了不同照相参数条件下带电粒子束对密度梯度靶照相的散射调制现象的特征.提出了一个与照相条件有关的无量纲参量,给出了其取值范围与散射调制特征的关系以及在实验诊断中的作用.

2 模型描述

对于带电粒子束照相,当带电粒子在靶内传输时与靶原子发生碰撞改变运动方向,即产生散射效应,同时通过碰撞、激发和电离原子核外电子损失能量.当带电粒子动能很高,在靶内能量损失可忽略,主要产生小角散射效应:带电粒子与靶原子发生多次碰撞,而每次碰撞只是轻微改变带电粒子的运动方向,散射角分布可近似为高斯分布[16,22].

如图1 所示,一束极细、准直的高能带电粒子束正入射到平面靶上一点,在靶内传输时发生小角散射.统计理论指出带电粒子穿过靶后产生的横向位移很小[22],即带电粒子束在靶内近似沿直线(z方向)向前传播.带电粒子束从靶后表面出射后变为锥状发散束,对应的散射角特征宽度为Ф.该发散束投射到与靶后表面距离为L的探测面上的归一化通量密度分布F(x)可用高斯分布描述[22]:

图1 准直带电粒子束被平面靶散射后的角分布示意图Fig.1.The schematic diagram of the angular distribution of a collimated charged particle beam scattered by a plane target.

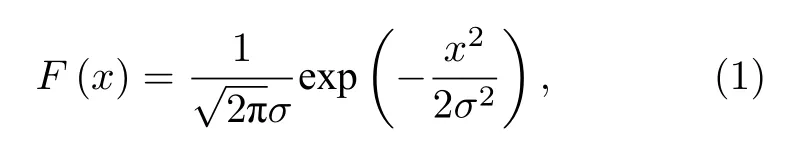
其中σ是高斯分布的标准差或特征宽度,σ=Φ·L.

散射角Φ和带电粒子能量、电荷量,以及靶物质性质的关系由Highland 经验公式给出[17,23]:

其中c是真空光速,β是入射带点粒子速度与真空光速的比值,p是带电粒子的动量,单位为 M eV/c,z是带电粒子的电荷量,Ρ是带电粒子通过的靶物质面密度,X0对应靶物质的辐射长度[23]:

其中Z和A分别是靶物质的原子序数和原子量.对于多种元素化合物或混合材料的靶物质,X0使用下式计算[23]:

其中wi和分别是第i种元素的质量比例和辐射长度.当靶由多层物质组成时,(2)式中P/X0为

其中Pi和分别是第i层物质的面密度和辐射长度.(2)式—(5)式表明,一束准直的高能带电粒子束穿过靶物质后,发散角宽度近似与穿越靶物质的面密度平方根成正比,与靶的材料成分也有关.

下面考察由点源发射的锥状带电粒子束对靶的照相:入射到靶前表面每一点的子束从靶后表面出射后,在探测面上都有一个高斯分布的通量密度分布,此分布的特征宽度与所在靶位置的材料组分和面密度有关.不同靶位置的材料或面密度不同,高斯分布的特征宽度也不同.因此,透射带电粒子束在探测面上总的通量密度分布是穿过靶的所有子束投射到探测面上的高斯分布的叠加,即对 (1)式的高斯分布做卷积运算得到.

考察沿探测面上x方向的通量密度分布.如图2(a)所示,设带电粒子束从点源O点发射,点源与靶前表面的距离为l,薄膜靶厚度为lz,探测面与靶后表面的距离为L.设一束均匀发散束照射到靶前表面,其中一子束打在位置x0,在靶内通过的面密度为P(x0),穿过靶后透射束的散射角宽度Φ(x0)由(2)式给出.该子束中心在探测面上的几何投影位置为ξ=x0·M,M=(l+L)/l是探测面上图像相对于靶的横向放大倍数.该子束在探测面上的特征宽度为σ(ξ)=Φ(x0)·L,归一化通量密度分布为

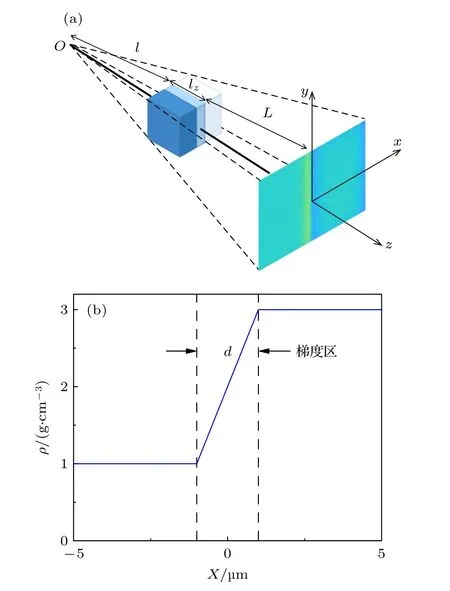
图2 带电粒子束照相一维密度梯度分布靶 (a) 照相示意图;(b) 梯度靶的密度分布示意图Fig.2.A charged particle beam radiographs a planar target with a one-dimensional density gradient:(a) The schematic diagram of radiography;(b) the schematic of density profile around the density gradient region.

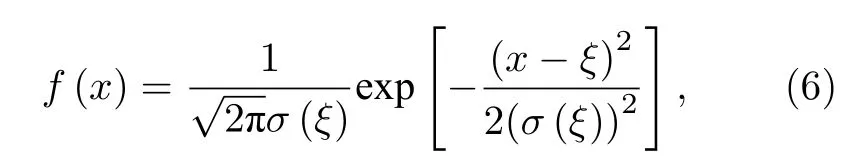
因此,带电粒子束穿过靶后,透射束在探测面上总的通量密度分布是对 (6) 式做卷积运算:

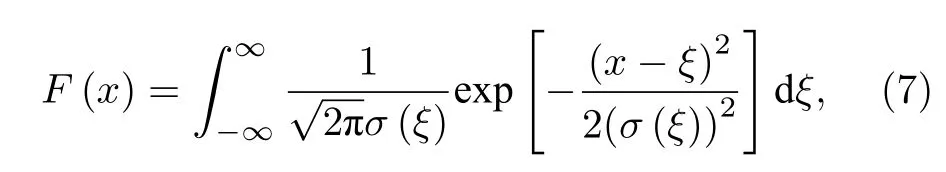
F(x)即为带电粒子束对靶照相,探测面上沿x方向的通量密度分布.对于非点源或非均匀发散束情况,可从(7)式推广得到.

由以上结果可知,无论采用离子(质子)束还是电子束照相,均可使用这个解析模型,主要区别是带电粒子的参数不同导致散射角宽度不同.

3 与蒙特卡罗模拟结果的比较与分析

以电子束照相为例,分别使用第2 节的解析模型和蒙特卡罗程序Fluka[21],模拟电子束对几类典型密度梯度分布靶的照相.将两种方法得到的结果进行比较,以确认解析模型的可靠性.在此基础上,使用解析模型分析密度梯度区对带电粒子束散射产生的调制信号特征及照相参数条件的影响.

3.1 一维密度梯度靶

平面靶的烧蚀区、激波前沿,以及靶界面等处的微米或亚微米量级宽的陡峭密度梯度区,其密度分布可用一维线性分布描述.电子束照相如图2(a)所示,动能为E的电子束从O点以一定发散角均匀发射,沿z轴穿过含横向密度梯度区的薄膜靶,薄膜厚度为lz,透射电子被探测面接收.靶的密度梯度区沿x方向,线性密度梯度区宽度为d,梯度区两侧的靶材料组分或密度不同,见图2(b)所示.除另有说明,设靶的长度和宽度无限大,密度梯度区的中点为坐标原点,电子束中心、坐标原点和探测面中心都在z轴上.

首先,模拟电子束对薄膜靶与真空界面的照相.靶为厚度30µm的铝膜,密度为入射电子束是平行束,相当于l=∞,电子动能E=40 MeV.设置探测面的长和宽都为3 cm,距离靶L=10 cm.根据(3)式,可以得到铝的辐射长度X0=24.28 g/cm2.使用解析模型,即(7)式,计算电子束对铝膜-真空界面照相,得到探测面上的电子通量密度分布,见图3(a).图中,x＜ 0,x=0,x＞ 0 分别对应真空、铝-真空界面、铝在探测面上的几何投影位置或区间.可以看到,对应铝-真空界面,通量密度分布出现一个明显峰谷结构的调制信号:谷出现在铝靶一侧,峰出现在真空一侧.远离界面的其他区间,通量密度分布均匀.原因是,接近铝-真空界面,铝靶一侧的入射电子被铝材料散射,部分电子被散射到真空一侧.离开界面较远的铝靶其他区,入射电子也会受到材料的散射作用,但对应靶面各点的入射电子子束的散射分布相同,因此按 (7) 式得到的总通量密度分布均匀.

与电子束、靶、探测面位置的设置相同,用Fluka 程序也模拟了电子束照相.模拟中使用的电子总数为 107,探测面均匀划分为 1000×1000 个网格,每个网格长和宽均为0.003 cm.对探测面上信号沿y轴方向做平均,得到沿x方向的电子通量密度分布(图3(a)).比较解析模型和Fluka 模拟的两个结果,二者符合得非常好.从图3(a)还可看到,Fluka 模拟因为使用了蒙特卡罗方法,得到的通量密度分布显示出细微抖动,而解析模型给出的分布是光滑的.

文献[18]的Fluka 模拟和文献[19]的其他蒙卡模拟表明,入射电子束的能量发散对这样的散射调制信号的影响可忽略.原因是,在MeV 或更高能量范围,电子弹性散射截面随电子能量的变化很小.本文也使用解析模型分析了能散的影响.其他参数条件与图3(a)相同,只是将40 MeV 单能电子束换为能谱为高斯分布的电子束:能谱中心的能量仍为40 MeV,能谱半高全宽处的能量范围分别设为中心能量的50%和100%,即能散分别为50%和100%.图3(b)给出了这样能散的电子束照相,探测面上的电子通量密度分布.为便于比较,图3(b)也含图3(a)的单能结果(即能散为0).结果表明,能散对调制信号的影响很小,和文献[18,19]中结论一致.

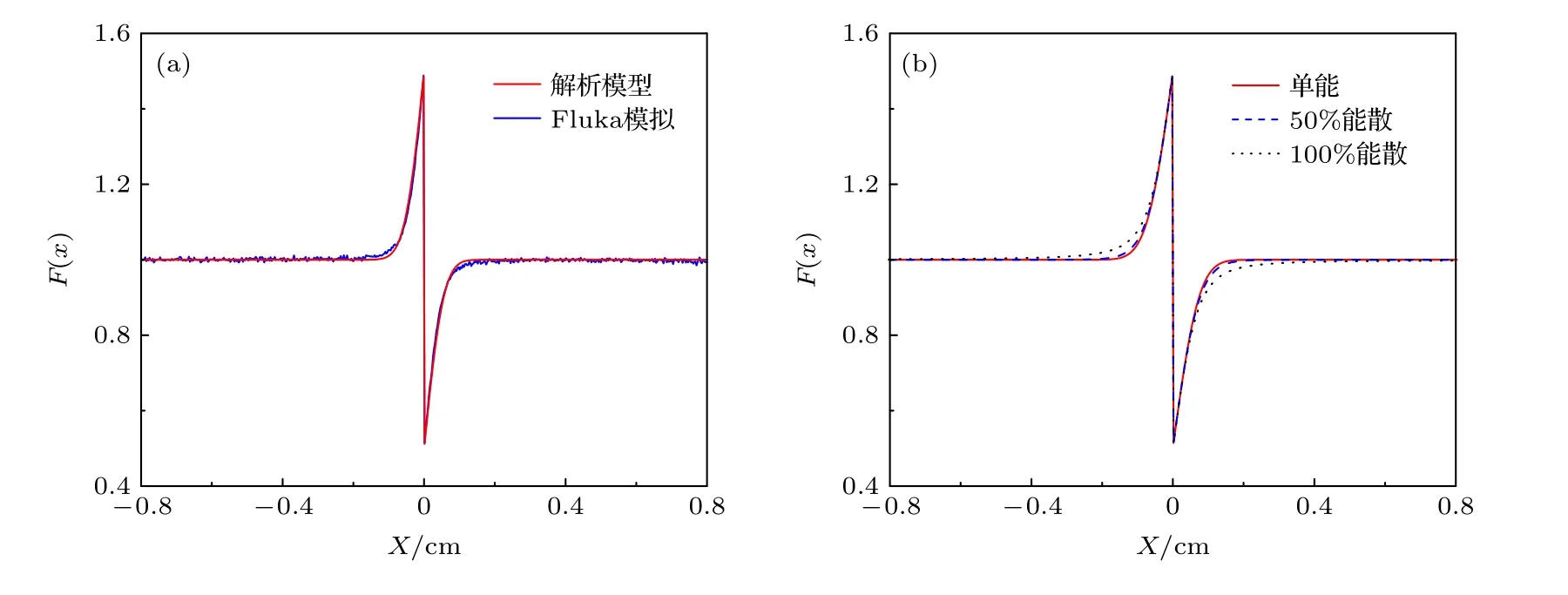
图3 沿x 方向的电子通量密度分布 (a)单能电子束;(b)不同能散电子束Fig.3.The electron fluence distribution along x direction for an incident electron beam:(a) Mono energy;(b) different energy spread.

其次,对于有一定梯度区宽度的靶,也分别比较了解析模型和Fluka 模拟得到的照相结果.这里使用了E=200 MeV 的点源发散束,发散角为200 mrad,l=0.1 cm.密度梯度靶是厚度为30 µm的PS 薄膜,见图2(b),线性密度梯度区的宽度分别设为d=1 µm 或0,后者对应台阶靶,两侧密度分别为 1 g/cm3和 3 g/cm3.对于PS 材料,按(3)式和(4)式计算的辐射长度为 44.06 g/cm2.设置探测面距离L=20 cm.使用解析模型,即(7)式,计算出照相在探测面上的电子通量密度分布,以及Fluka 模拟的结果,分别示于图4 中.结果表明二者符合很好.另外,图4(a)给出台阶靶产生的散射调制信号的峰、谷两区域具有很好反演对称性,即相对于峰、谷位置的中点,谷区做180°旋转,与峰区在形状、宽度和深度上都重合很好.图4(b)给出宽度d=1 µm 的线性梯度靶产生的散射调制信号则呈现出峰谷不对称的特点.原因是,入射到线性梯度区宽度内的电子子束的散射角宽度高于低密度一侧的,经过散射后,部分电子偏转到低密度一侧.梯度宽度区拓宽了散射调制信号的谷区,导致散射调制信号的峰、谷失去对称性.

图4 沿x 方向的电子通量密度分布 (a) d=0 µm;(b) d=1 µmFig.4.The electron fluence distribution along x direction:(a) d=0 µm;(b) d=1 µm.

3.2 多层球靶

用于惯性约束聚变等研究的典型靶是由不同材料构成的多层球形靶丸.文献[15,18]使用Fluka 模拟了电子束对这种结构靶的照相,本文比较Fluka 和解析模型分别模拟对多层球靶照相的结果.图5给出了照相示意图.设点源发射束的发散角为300 mrad,电子动能为100 MeV,电子总数为108,沿z轴方向对多层球形靶丸照相.设靶丸置于真空中,靶丸中心位于坐标原点.电子源与靶丸中心的距离l=1 cm.靶丸有3 层结构[2,15],由内向外半径分别是R1=0.087 cm,R2=0.095 cm,R3=0.108 cm.最内层区域为氘氚混合气体,密度为0.3 mg/cm3,氘和氚的原子数比为29∶21.中间层区域是氘氚固体,密度为0.25 g/cm3,氘和氚的原子数比也是29∶21,最外层区域是掺铜的铍金属壳,密度为1.9 g/cm3,铍和铜的原子数比为991∶9.探测面与原点的距离L=20 cm,大小为8 cm × 8 cm,等分为1000×1000 个网格.探测面中心位于z轴上.按照这些设置,照相的横向放大倍数M=21 .

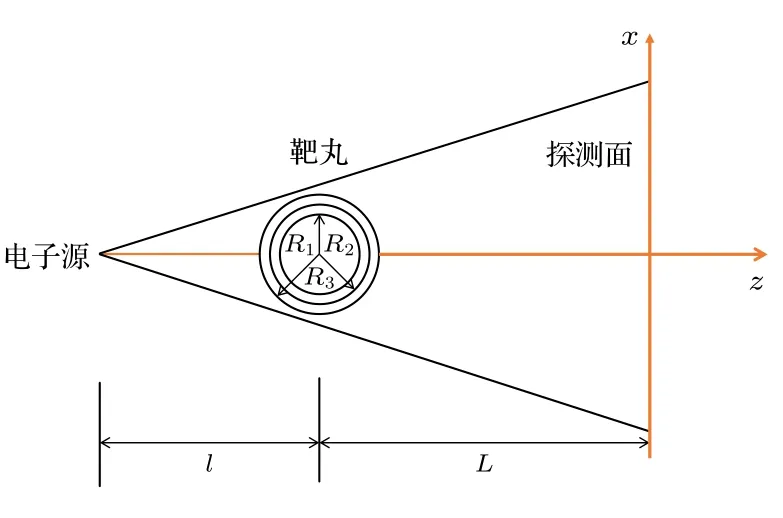
图5 电子束对多层球靶照相的示意图Fig.5.Schematic diagram for an electron beam radiographing a spherically multilayer capsule.

使用Fluka 模拟电子束照相,在探测面上的图像见图6(a).为完成这个模拟,主频为2.8 GHz 的计算机运算超过60 h.图6(b)是对图像沿y轴方向中心(y=0)两侧4 个网格的数据做平均后,得到的沿x方向的电子通量密度分布.图中竖线对应横坐标是电子源点经过球靶各层的外球面切点在探测面上的几何投影位置,分别是x=1.827 cm,x=1.995 cm,x=2.268 cm.可以看到,在球靶的边缘,即球靶边沿-真空界面附近,有明显散射调制现象.在边沿外侧,即在真空区出现峰,内侧出现较宽区间的谷区.而对应靶丸内层两个界面,虽有通量密度分布的调制,但信号较弱,没有明显的峰-谷结构现象[15,18].由于球靶的层间间隔小,内层两个界面的调制信号与球靶边沿-真空界面的调制信号谷区发生了重叠.

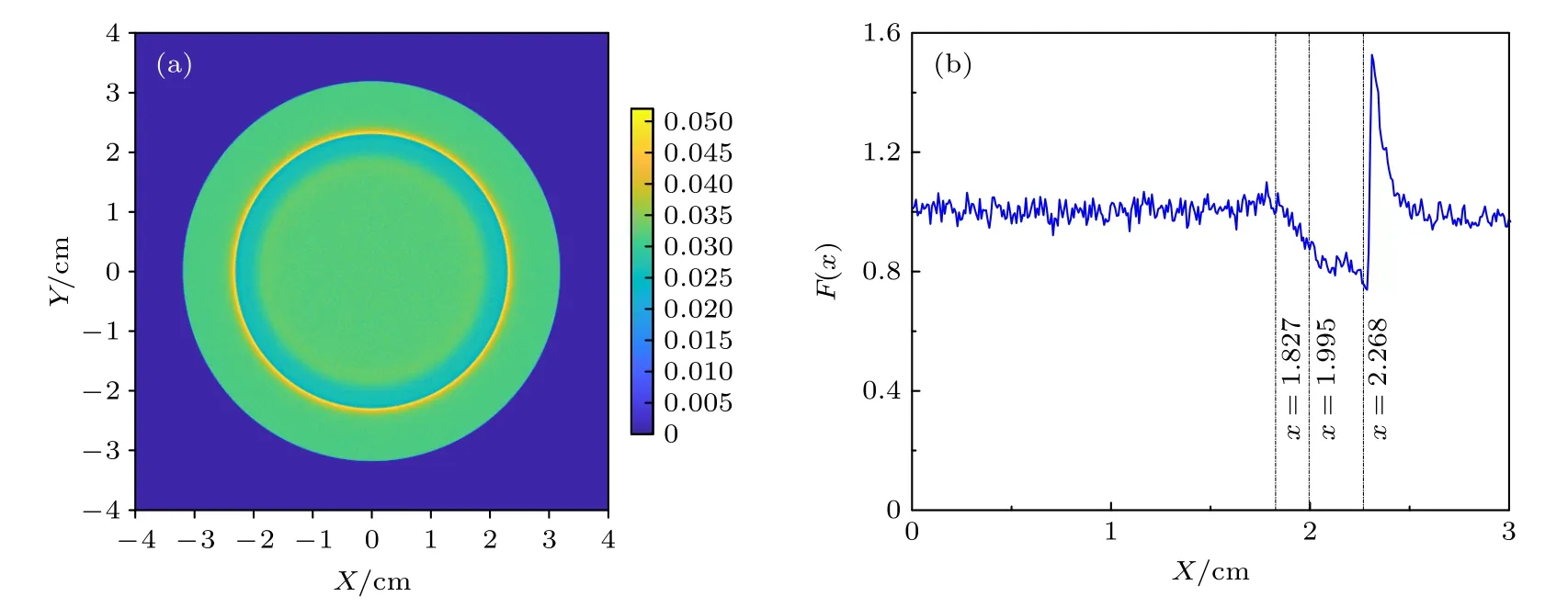
图6 Fluka 模拟结果 (a) 探测面上电子图像;(b) y=0 附近沿x 方向的通量密度分布Fig.6.Results from Fluka simulation:(a) Electron radiograph on the detection plane;(b) fluence distribution along the x direction around y=0.

在相同照相条件下,使用本文的解析模型也模拟了这一照相.电子在靶内近似直线传输,使用(2)式,计算从电子源发射的发散束入射到球靶不同位置的电子子束的散射角宽度Φ沿横向(x或y方向)的分布,如图7(a)所示.由于入射到球靶不同横向位置的电子子束从靶出射的纵坐标位置(z)不同,对图7(a)的横坐标进行近似,都取在z=0 处.从结果可见,虽然球靶沿径向有三层结构,且不同层间密度差别大,但到达靶丸不同横向位置的电子子束经过的面密度是连续变化的,散射角宽度也是连续变化的.图中标出了球靶的三层界面位置.在x=0 到0.087 cm 的第一层,散射角宽度缓慢增大.在第二、三层的界面,x=0.095 cm,散射角宽度达到极大值.随着x增大到第三层外边界,x=0.108 cm,散射角宽度下降到0.

图7 解析模型的结果 (a) 散射角宽度的径向分布;(b) y=0 处通量密度分布和Fluka 模拟结果Fig.7.Results from the analytical model:(a) Distribution of the scattered angle in the radial direction;(b) the fluence distributions from the analytical model and Fluka simulation,respectively.

使用解析模型((7)式),计算得到电子束照相在探测面上y=0 处的通量密度分布,示于图7(b)中.图中竖线对应横坐标是电子源点经过球靶各层外边界切点在探测面上的几何投影位置.为便于比较,将Fluka 模拟结果,即图6(b)也画在图7(b)中.可以看到,解析模型与Fluka 模拟给出的探测面上通量密度分布具有相同特征.如前解释,在球靶的边缘,即球靶边沿-真空界面附近,有明显的散射调制现象.从图7(a)可见,在此区间散射角宽度有明显的变化.而在其他区间,散射角宽度随位置的变化相对小些,散射调制现象也相应弱些.

图7(b)也显示,由解析模型给出的球靶-真空界面产生散射的峰位置(x=2.28 cm)与Fluka 结果(x=2.31 cm)相比,相对偏离了1.3%.这是由于在得到图7(a)的散射角时,对(2)式以及(7)式中的横坐标取值做了近似.从图7(b)的结果可见,这个近似仅带来很小位置偏差,不影响散射调制信号特征.

值得指出的是,使用解析模型给出探测面上通量密度分布,即图7(b)的结果,计算机运算时间短于1 s,远小于Fluka 模拟所用机时(超过60 h).而且,从以上对几类典型密度梯度分布靶照相的处理来看,相对于蒙特卡罗方法,使用解析模型能快速、准确获得电子束对靶照相及密度梯度区散射影响的结果,证明了该模型的可靠和计算省时.

3.3 散射调制信号特征与照相条件优化

鉴于解析模型的快速有效,本节采用解析模型分析带电粒子束对密度梯度靶照相,探测面上散射调制现象的特征,以及利用这些特征来诊断密度梯度区对照相条件的要求.

为了描述探测面上散射调制信号的特性,定义两个特征量,一是调制信号的对比度:

式中,Fmax和Fmin分别代表调制信号的通量密度峰值和谷值.第二个特征量是调制信号的峰谷间距dpv,表示峰值与谷值所在位置的间距.

首先给出平行束或点源发散束对类似图4(a)所用台阶型密度分布靶的照相特征.参见图2,设点源发散束满足傍轴条件,即所有子束入射到台阶附近的靶面时与z轴的夹角很小.台阶两侧的靶物质或面密度不同,带电粒子穿过两侧物质后散射角宽度也不同,分别用Φ1和Φ2表示.那么探测面上的高斯分布的标准差分别为σ1=Φ1·L,σ2=Φ2·L.代入(7)式得到探测面上的通量密度分布:

由此可知,散射调制信号具有很好反演对称性.对比度为

从(9)式还可得到调制信号的峰谷间距:

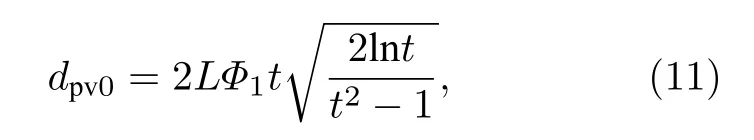
可见dpv0与靶物质产生的散射角宽度、靶到探测面的距离L成正比,和台阶靶两侧物质产生的散射角宽度的比值也有关系.增大L可增大调制信号的峰谷间距,使得调制信号更易被记录和观察.

不同于台阶靶,对于像图2(b)或图4(b)中密度梯度区宽度非零的梯度靶的照相,无法得出类似于(10)式和(11)式调制信号对比度与峰谷间距的解析表达式,需要对(7)式进行数值计算,才能给出探测面上通量密度分布及散射调制信号特征.本文通过分析改变照相参数的数值计算结果发现,可使用一个无量纲参量ω,从其取值范围能够判断带电粒子束对密度梯度靶照相产生的散射调制信号的特征.其定义为ω=Md/dpv0,其中d是梯度区宽度,M是照相的图像横向放大倍数,Md即是梯度区宽度在探测面上的几何投影宽度.dpv0是其他条件不变的情况下梯度区宽度为0 时探测面上调制信号的峰谷间距,反映了散射效应,由(11)式给出.将M和(11)式代入ω,得到

可见,ω的取值和点源到靶的距离l,靶到探测面距离L,梯度区宽度d和两侧散射角宽度都有关.

图8 给出了不同参数的照相条件下散射调制信号的典型形状与ω取值的例子.取l=0.1 cm,d=1 µm,Ф1=0.286 mrad,t=1.98,L=20 cm,计算得到的调制信号示于图8(a),显示峰谷不再对称,谷有更大的展宽.该条件下的对比度κ=10.53%,峰谷间距dpv=220.1 µm,ω=1.30.相对于图8(a)的条件,改变梯度宽度d或带电粒子束源点与靶的距离l,而其他参数不变,计算得到的调制信号示于图8 的其他图中.其中沿横向的图8(b),(a),(c),只是改变了梯度区宽度.可以看到,图8(b)中,d=0.2 µm,ω=0.26,调制信号基本对称,κ=15.49%,dpv=156.1 µm,和台阶靶(d=0)的调制信号接近.图8(c)中,d=5 µm,ω=6.49,峰和谷完全分离,dpv=1006.7 µm,该值接近梯度区宽度在探测面上的几何投影宽度.不过其对比度下降到了2.23%.对于实验诊断,通常要求对比度不低于5%,更低对比度的散射调制信号难以被观察到.

图8 中沿纵向的(d),(a),(e)三图,只改变了带电粒子束源点与靶的距离l,即改变了带电粒子束的发散角.可看到调制信号随ω变化的同样规律.综上可见:当特征参量ω改变时,调制信号的形状、对比度、峰谷间距都有相应改变.然而,无论改变梯度区宽度还是带电粒子束源点与靶的距离,只要ω取值相同,调制信号就具有相同特征.

设置其他照相参数条件与图8(a)相同,图9(a)—(c)分别给出仅连续改变其中一个照相参数,分别是梯度区宽度d、探测面距离L、入射束源点与靶距离l或入射束发散角,计算得到对比度和峰谷间距等散射调制信号特征量以及参量ω的变化关系.

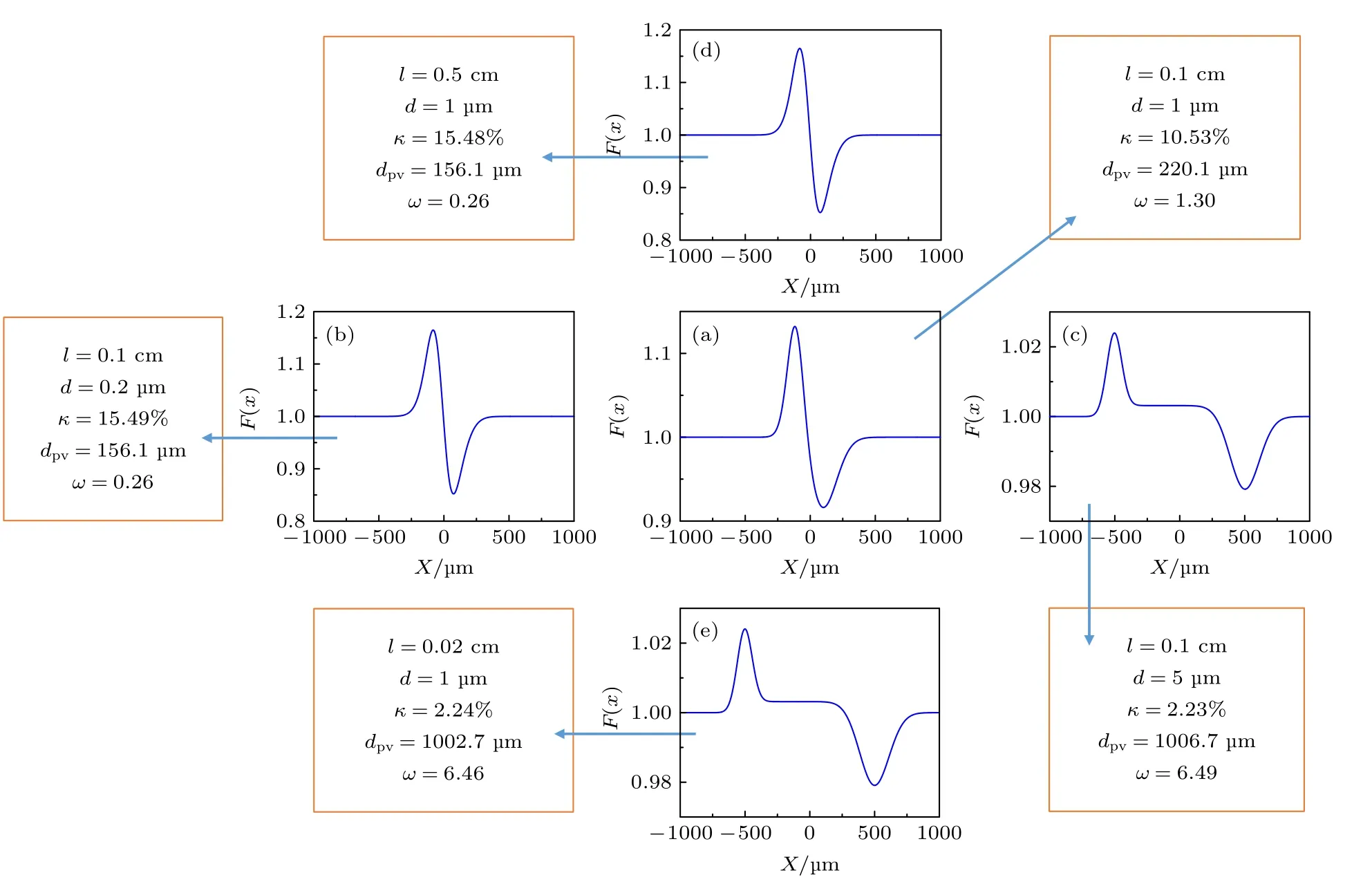
图8 不同照相参数条件下典型调制信号形状Fig.8.Representative modulation structures under different radiography conditions.

图9(a)给出入射束为点源发散束时,梯度区宽度变化对散射调制信号的影响.由 (12)式可知,特征参量ω与梯度区宽度d成正比.从图9(a)可见,当d或ω很小时,对比度和峰谷间距接近台阶靶情况(图中d=0 时).随着d或ω的增大,对比度和峰谷间距相应改变.当d＞ 2.3 µm 或ω＞ 2.9时,峰谷间距已经与梯度区宽度的几何投影尺寸Md相等,然而对比度下降到5%以下,实验中难以观察到散射调制信号.这些结果表明,若使ω＜2.9,就可从实验中获得对比度和峰谷间距这些特征量.结合其与梯度区参数的对应关系,例如图9(a)中梯度区宽度,就可能诊断出梯度区参数等信息.

从图9(a)可见,在该照相参数下,适于诊断的梯度区宽度d＜ 2.3 µm.对于d＞ 2.3 µm 的梯度区宽度,为了能实现对其诊断,可通过调节实验参数,从 (12) 式可见,增大l可使ω小于2.9.不过,对这样大的梯度区宽度,有X 射线诊断等成熟手段,而本文针对的是X 射线照相难以诊断的d≲2 µm的陡峭密度梯度区.

图9(b)是固定探测面距离L=20 cm,给出了带电粒子束源点与靶的间距l改变时对散射调制信号的影响.可以看到,尽管靶的梯度区宽度为1.0 µm,但是随着l增大,即照相束的发散角变小,对比度和峰谷间距会趋于台阶靶情况,并且ω趋于零.这一结果表明,若使用平行束(发散角为零)照相,不利于分辨不同梯度区宽度.另一方面,当l减小到一定值时,尽管dpv趋于与Md相同,但是对比度会下降到5%以下,难以观测到散射调制信号.因此,适当控制带电粒子束的发散角,即选择参数l,才有助于诊断.

图9(c)针对发散束(l=0.1 cm)和平行束(l=∞)照相两种情况,给出了峰谷间距dpv随探测面与靶后表面的距离L的变化.从结果可见,当探测面离开靶后表面一定距离后,对比度趋于稳定.而且,dpv随L线性增大,和台阶靶情况(见 (11) 式)类似.这些性质有利于实验探测散射调制信号.图中还显示,对于平行束,在L很小时,dpv随L偏离线性变化.这是因为在L很小时,梯度区在入射束照射下的几何投影Md决定了dpv.随着L增大,dpv很快超过Md,随L就表现出很好线性关系.

从图9(c)还可看到采用发散束照相的优点.由于l取有限值,由 (12) 式可见,不仅可以满足ω＜ 2.9,而且(1/l+1/L)随着L的增大趋近于1/l,ω趋于一稳定值,即散射调制信号的特征稳定,有利于实验探测.而且,采用发散束放大照相图像使dpv更大,对探测器的空间分辨要求降低,便于探测,也有助于在探测面上分开靶或入射束的边缘产生散射对陡峭密度梯度区产生散射调制信号的干扰[18,19].

图9 调制信号特征量和ω 随照相参数的变化 (a) 点源发散束情况下改变梯度区宽度;(b) 改变点源与靶的间距;(c) 点源发散束和平行束条件下改变靶与探测面距离;(d) 无量纲的调制信号特征量随ω 的变化关系Fig.9.Dependence of the characteristic quantities and ω on the change of:(a) Density gradient width by using a point-source beam for radiography;(b) point source-to-target distance;(c) target-to-detection plane distance by using a parallel beam or a point-source beam for radiography,respectively;(d) the relation of the dimensionless characteristic quantities to ω.

总结图9(a)—(c)发现,若采用无量纲形式,无论改变d,l或L哪个照相参数,κ,dpv/L,Md/L和dpv0/L随ω的变化关系都遵循同样规律,见图9(d).对比度会随着ω的增大而下降.当ω＞ 2.9时,对比度下降到5%,不利于实验观测散射调制信号.dpv/L会随着ω增大,从与dpv0/L重合逐渐增大到和Md/L重合.当ω接近零时,dpv/L与dpv0/L重合,梯度区宽度非零的靶与台阶靶的峰谷间距一样,易出现在平行束照相情况.因此,采用发散束照相,且选择照相参数使ω在适当范围,梯度区宽度变化对散射调制信号的影响比较明显,而且调制信号的对比度也足够大,才可能通过实验观测散射调制信号特征来诊断陡峭密度梯度区信息.

最后,需要说明的是,本文的解析模型及以上分析基于带电粒子在靶内沿直线传输这一近似,适用于靶厚度或面密度不大的“薄膜靶”情况.带电粒子在靶内散射的横向位移可近似为散射角特征宽度Ф和靶厚度lz的乘积Φ·lz.相对于靶的横向梯度区宽度d,带电粒子在靶内沿直线传输这个条件可以近似表示为Φ·lz≲d.对于厚靶或面密度大的靶,lz或Ф变大,这个条件不成立,是否能给出解析模型需要进一步研究.

4 结论

本文基于高能带电粒子在靶内传输时发生小角散射效应,发展了一个描述散射效应的解析模型,用于分析带电粒子束对薄膜或面密度不大的靶照相时陡峭密度梯度区产生的散射效应.针对几类典型密度梯度靶的照相,通过比较解析模型和蒙特卡罗数值模拟结果确认,解析模型给出的结果和蒙卡模拟符合很好,计算机时显著减少,证实了该模型处理散射效应的可靠和有效.使用这个解析模型,获得并分析了带电粒子束对陡峭密度梯度区照相产生的不同形状散射调制信号及特征.发现可用一个与照相条件有关的无量纲参量ω来判断散射调制信号的特征.对改变照相条件参数的分析表明,采用发散束照相并选择照相参数使ω 在适当范围,梯度区宽度变化对散射调制信号的影响比较明显,且调制信号的对比度足够大,才有可能通过实验观测散射调制信号来诊断宽度 ≲ 2 µm 的陡峭密度梯度区.本文提出的解析模型和取得结论可为带电粒子束照相的散射效应分析和实验选择照相参数条件提供理论基础与指导.感谢张宇在发展解析模型工作中的贡献.